Stability Analysis for the Deployment of Unmanned Surface Vehicles

1. Introduction

A Unmanned Surface Vehicle (USV) is an autonomous or remotely operated system which is deployed and a wide area of water surface. Since the master plan was first officially released by US Navy in 2007, USVs have received much attention by ocean engineers [1]. As global positioning systems have become more compact and affordable, USVs have become more capable. As a group of autonomous vehicles, USVs are successfully deployed for military operations, search and rescue missions and environmental monitoring as well as tactical oceanography [2]-[4].

In particular, USVs can be used as a mobile interface between heterogeneous unmanned systems such as unmanned underwater vehicles (UUVs) under the sea surface and unmanned aerial vehicles (UAVs) over the sea surface. Acoustic devices are used to communicate with UUVs, and signals are converted and transferred to UAVs via radio frequency communication. Air to underwater data transmission is also a feasible example of USV as a mobile interface.

USVs can be deployed to form a decentralized network, distributed over a spatial area, to provide real-time sensory information with the benefits of scalability, modularity and robustness. A dynamic topology permits the formation of the USVs to optimally position and align its sensors to improve sensing metrics such as error covariance and signal-to-noise ratio (SNR), fast response to dynamically changing environments. Such a formation can then be made autonomous giving each USV decision making capabilities based on the information which is collected by its own sensors.

A human in the loop provides initial directives to a group of USVs regarding location, area of surveillance/mapping and data requested, and USVs then configure their operational mode depending on their required function. Deployment of USVs ultimately depends on the ability to position each vehicle so that it is able to collect data from its surrounding environment in an optimal manner. There are situations where the USVs will reach equilibrium with respect to their spatial distribution (topology), in which case the formation can essentially become stationary once such a configuration is reached.

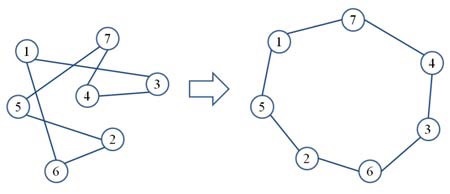
Figure 1 shows the transition from the arbitrary initial USVs positions to the desired final distribution. To reach this final configuration, each vehicle exchanges information with a small subset of the formation, specifically those USVs which are within the range of its wireless communication or sensor capability. As the range of such hardware may be limited, the basic problem faced by a group of USVs is how to use local information to decide one’s motion so that a global goal is achieved. This is generally achieved by coming up with force-laws that translate the position and/or velocity information being exchanged by the vehicles into force commands for their actuators. [5] presents some force-laws which cause a group of agents to arrange itself in a pattern of hexagons or squares.

Figure 1:

Move from their arbitrary initial positions to the desired topology

In literatures, motion control scenarios of USVs are usually classified into three main categories (point stabilization, trajectory tracking, and path following), along with the concept of path maneuvering [6]. Among those control issues, the goal of point stabilization is to stabilize the vehicle zeroing the position and orientation error with respect to a given target point with a desired orientation (in the absence of currents). The goal cannot be achieved with smooth or continuous state-feedback control laws when the vehicle has nonholonomic constraints.

Because of hardware constraints, force-laws cease to be effective when the robots move a certain distance away from each other and the graph representing the communication between vehicles keeps changing as the USVs move. Therefore, in addition to the final steady state of the formation, information about the transients is required.

In the following sections, stability properties of the formation are analyzed to determine transient properties, tracking performance and capability to reject noise or disturbances.

2. Mathematical Preliminaries

2.1 Graph Theory

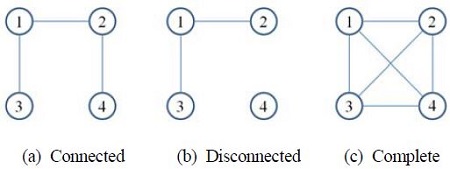
A graph G consists of a set of unique vertices, denoted V, and a set of edges, denoted E. Each element of the set Econnects two distinct elements of the set V, meaning thatthe graph has no self-loops. We also assume that eachelement of E is unique. Elements of the set E, and hencethe graph they define, can be directed or undirected. In ourwork, the graphs we define are always undirected. If everypossible edge between all possible pairs of the elements of V exists, the graph is said to be complete.

A path on G of length N from υ₀ to υ_N is an ordered set of distinct vertices [υ₀…υ_N] such that (υ_i-1,υ_n) ∈ E, ∀i ∈ [i,N]. A graph in which a path exists from every vertex to every other vertex is said to be connected. A graph in which disjoint subsets of vertices exist that cannot be joined by any path is termed disconnected. An N-cycle on G is a path for which υ₀ = υ_N.

A graph without any cycle is said to be acyclic. A graph with the property that the set of all cycle lengths has a common divisor k > 1 is said to be k-periodic. The relationship between graph theory and control theory makes use of matrices associated with a graph. For the purpose of defining these matrices, it is assumed that the vertices of are enumerated, and each is denoted υ_i. Given a graph with vertex set V and edge set E , the Adjacency Matrix Ad is defined as,

$\[ {\displaystyle {\left(ad\right)}_{ij}=\{\begin{array}{c}1if({\upsilon }_i,{\upsilon }_j)\in E\\ \mathrm{0 }\text{overwise}\end{array}} \]$

(1)

Since no self loops are allowed, (ad)_ii = 0, ∀i. The graph Laplacian is then defined as

$\[ {\displaystyle \text{L=D-Ad,}} \]$

(2)

where D is a diagonal matrix whose i^th diagonal entry is the number of neighbors of υ_i, i.e. the number of other vertices it is connected to. For the graph shown in Figure 2 (a), the Laplacian will be

Figure 2:

Connected, Disconnected, and Complete Graphs

$\[ {\displaystyle L=\left(\begin{array}{c}\text{2}\text{-1}\text{-1}\text{0}\\ \text{-1}\text{2}\text{0}\text{-1}\\ \text{-1}\text{0}\text{1}\text{0}\\ \text{0}\text{-1}\text{0}\text{1}\end{array}\right)} \]$

(3)

Note that the rows of L each sum to zero.

2.2 Differential Equations with Discontinuous Right Hand Side

Let us consider the vector differential equation

$\[ {\displaystyle \stackrel{.}{x}=f(x,t),} \]$

(4)

where f:Rⁿ × R → Rⁿ is discontinuous but measurable and essentially locally bounded. In mathematics, a generalized concept of ordinary differential equation is expressed as differential inclusion.

A vector function x(⋅) is called a solution of Equation (4) on [t₀,t₁] if x(⋅) is absolutely continuous on [t₀,t₁] and for almost all t∈ [t₀,t₁]

$\[ {\displaystyle \stackrel{.}{x}\in K\left[f\right](x,t)} \]$

(5)

where

$\[ {\displaystyle K[f\mathrm{](}x,t)\equiv \bigcap _{\delta >0}\bigcap _{\mu N}\stackrel{─}{\mathrm{co}}f(B(x,\delta )-N,t)} \]$

(6)

and $$ {\displaystyle \bigcap _{\mu N}}$$ = 0 denotes the intersection over all sets of natural number N of Lebesgue measure(μ) zero. $$ {\displaystyle \overline{co}}$$ is a convex closure of the function f. B is an open ball of radius δ centered at x. Equation (6) also means that there exist N_f ⊂ Rⁿ, μN_f = 0 such that for all N⊂ Rⁿ, μN = 0,

$\[ {\displaystyle K\left[f\right](x,t)\equiv co\{limf\left(x_i\right)\mid x_i\to x,x_i\notin N_f\cup N\}} \]$

(7)

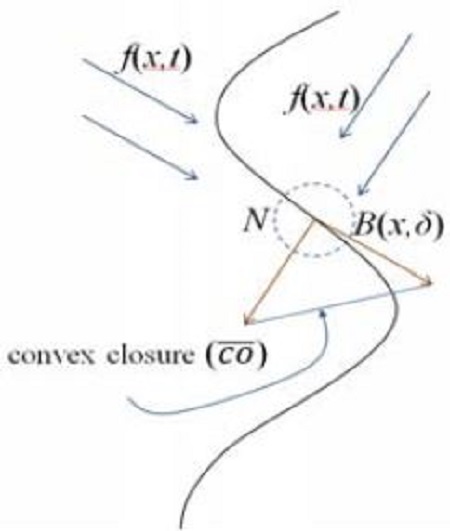
The content of Filippov’s solution is that the tangent vector to a solution, where it exists, must lie in the convex closure of the limiting values of the vector field in progressively smaller neighborhoods around the solution point. It is important in the above definition that sets of measure zero are discarded. This technical detail allows solutions to be defined at points even where the vector field itself is not defined, such as at the interface of two regions in a piecewise defined vector field (Figure 3). More details on this subject are available in [7][8].

Figure 3:

Solutions of Differential Equations with Discontinuous RHS

3. System Modeling

Let us start analysis by considering a network of a set of USVs, each having standard second order linear dynamics with viscous friction. Each USV has wireless communication devices which can function to a distance of say r units. All vehicles weigh 1 unit and are assumed to have identical dynamics and communication devices. As USVs move on sea surface, analysis is taken for 2-dimensional space. Then for i-th vehicle,

Here c is the viscous constant and f_ix and f_iy is the force that each USV exerts in the x and y direction respectively to propel itself so that the USV can reach to the final position with respect to other vehicles . The output is its current position x_i and y_i . So

Let n_n be number of vehicles in the network, and n_y be number of outputs per a vehicle = 2. It is assumed that the forces f_ix and f_iy have a certain structure as following.

In other words,

Here X is the stacked state vector of the entire system, i.e. $$ {\displaystyle X={[X_1^T...X_{n_n}^T]}^T}$$ and $$ {\displaystyle {\Psi }_i:R^{4n_n}\to R^2}$$ are possibly non-linear functions of X. The summation is over all the j "neighbors" of vehicle i, that is to say all the vehicles in the formation at a distance less than r units from the vehicle i. Let us consider a USVs where each vehicle behaves as if they are attached by springs of stiffness g and unstretched length r with their neighbors.

Then, the force being computed by each vehicle is,

where $$ {\displaystyle d_{ij}=\sqrt{{(x_i-x_j)}^2+{(y_i-y_j)}^2}}$$ , the distance between vehicles i and j. By setting $$ {\displaystyle U={[U_i^T...U_{n_n}^T]}^T}$$, and with Kronecker algebra notation,

But

where $$ {\displaystyle \Psi ={[{\Psi }_1^T...{\Psi }_{n_n}^T]}^T}$$ and L is the graph Laplacian defined above. After substituting Equation (14) in Equation (13), we have

Using the property (P⊗Q)(R⊗S) = PR⊗QS, if the dimensions are appropriate and due to the fact that the number of inputs to each node equals the number of outputs, Equation (15) can be simplified to

Now, consider the first part of Equation (16),

Now let us consider the imaginary center of gravity (CoG) of the USV formation. Since the dynamics in the y-direction are analogous to the ones in the x-direction, we only write out the x dynamics of the system below. Then,

$$ {\displaystyle x_{\mathrm{cg}}=\frac{1}{n_n}\sum _{i=1}^{n_n}{x}_i,{\dot{x}}_{\mathrm{cg}}=\frac{1}{n_n}\sum _{i=1}^{n_n}{\dot{x}}_i}$$

and

$$ {\displaystyle {\ddot{x}}_{\mathrm{cg}}=\frac{1}{n_n}\sum _{i=1}^{n_n}{\ddot{x}}_i,{\ddot{x}}_{\mathrm{cg}}=\frac{1}{n_n}\sum _{i=1}^{n_n}(-c{\dot{x}}_i-g\delta x_i)}$$

Therefore,

Because the term $$ {\displaystyle \sum _{i=1}^{n_n}\delta x_i}$$

is equivalent to 1^TLx and 1 is the eigenvector of the symmetric matrix L corresponding to the zero eigenvalue, the second term in Equation (18) is zero. Thus,

If the initial condition of the formation is such that $$ {\displaystyle \sum _{i=1}^{n_n}{\dot{x}}_i=0}$$ and $$ {\displaystyle \sum _{i=1}^{n_n}{\dot{y}}_i=0}$$ , the CoG of the entire system is stationary. Equation (19) also shows that the dynamics of the CoG is not subject to inter-vehicle forces. The CoG of the system, if it is subject to a non zero initial velocity condition, will eventually come to rest.

Now if we define $$ {\displaystyle Z=\mathrm{[...}{z}_{\mathrm{xi}}{\dot{z}}_{\mathrm{xi}}{z}_{\mathrm{yi}}{\dot{z}}_{\mathrm{yi}}{\mathrm{...]}}^T}$$ where

Then, by substituting Equation (19) into Equation (17), we have

Now $$ {\displaystyle Z=X-{[...{\mathrm{ x}}_{cg}{\stackrel{.}{\mathrm{ x}}}_{cg}{\mathrm{ y}}_{cg}{\stackrel{.}{\mathrm{ y}}}_{cg}]}^T}$$ . Therefore, we have

For the matrices B, C and any L, the second term of Equation (22) is zero. This is because the 1^T vector is and eigenvalue of L corresponding to the zero eigenvalue, and we have (L⊗BC)Z = (L⊗BC)X - (L⊗BC. Hence, we can rewrite Equation (21) as

Even though Equation (23) looks like a linear dynamical equation, the graph Laplacian is not constrained to be constant. It varies as a discontinuous function of the vehicle positions and thus the right hand side of this equation is discontinuous. The set of points at which it changes value are ones where one or more pairs of vehicles in the formation are at a distance r from each other. Between such points, there is a continuum of points where the Laplacian is constant.

It is notable that since the number of USVs is finite, there are a finite number of possible graphs, connected or disconnected. Thus there is a finite number of points at which a change of Laplacian takes place.

Let Ω be the set of zero measure of points at which the L matrix switches value and Ω_l, l = 1,2,...,q be the continuous sets of non-zero measure in which the graph is constant with the Laplacian L_l. Then the absolutely continuous function X(t) is a Filippov solution ([7] and Equation (6)) of Equation (23) if it satisfies the differential inclusion,

When the current state of formation Z(t) ∈ Ω_l, then K[f(Z)](Z) = f(Z). At the points of discontinuity, the derivative $$ {\displaystyle \stackrel{.}{Z}}$$ lies in the convex hull of the points representing the limits of the value of $$ {\displaystyle \stackrel{.}{Z}}$$ as Z approaches the point of discontinuity from various directions. So

$$ \begin{array}{c}K\left[f\right(Z\left)\right]\left(Z\right)=\sum _{l=1}^q{\alpha }_l(I_{n_n}\otimes A-g{L}_l\otimes BC)Z {\alpha }_l\ge 0,\sum _l{\alpha }_l=1\hfill \\ =(I_{n_n}\otimes A)Z-g\sum _{l=1}^1{\alpha }_l(L_l\otimes BC)Z\hfill \\ ={[{\stackrel{.}{z}}_{\xi },(-c{\stackrel{.}{z}}_{\xi }-g\sum _{l=1}^q{\alpha }_l\delta z_{\xi l}),{\stackrel{.}{z}}_{yi},(-c{\stackrel{.}{z}}_{yi}-g\sum _{l=1}^q{\alpha }_l\delta z_{\xi l}\left)\right]}^T\hfill \end{array}$$

where i = 1,2...,n_n. At points Z ∈ Ω_l, α_l=1 and all other α_l = 0. δz_xil and δz_yil are δz_zi and δz_yi corresponding to the graph represented by the Laplacian L_l.

4. Stability Analysis

To check the stability of the system described in Equation (23) which has a dynamic equation with discontinuous right hand side, we start with the Lyapunov Stability Theorem.

Lyapunov Theorem: Let $$ {\displaystyle \stackrel{.}{x}=f\left(x\right)}$$ be essentially locally bounded and 0∈K[f(x)](0) in a domain D ⊂ Rⁿ containing x = 0. Let x(⋅) be a Filippov solution of the system. Let V(x) : Rⁿ→R be a Lipschitz, regular function. Then,

1. V(x) is asolutely continuous, $$ {\displaystyle \stackrel{.}{V}\left(x\right)}$$ exists almost everywhere and

$$ {\displaystyle \frac{d}{\mathrm{dt}}V(x){\in }^{a.e}\dot{\tilde{V}}(x)}$$

where $$ {\displaystyle \dot{\tilde{V}}(x\mathrm{):}=\underset{\xi \in \partial V(x)}{\cup }{\xi }^{T}K[f\mathrm{](}x)}$$, and ∂ V(x) is the generalized gradient of V(x). In addition, the function V(x) satisfies that V(0) = 0, and V(x) ≥ 0 in D - {0}.

2. in D implies x = 0 is a stable equilibrium point.

3. in D - {0} implies x = 0 is an asymptotically stable equilibrium point.

Proof: See [9] and [10]. ￭

We not state the stability of the system described in the previous section.

Corollary 1: The dynamic system represented by Equation (23) is stable.

Proof: Let us choose the following Lyapunov function

where $$ {\displaystyle z_x,{\stackrel{.}{\mathrm{ z}}}_x,{\mathrm{ z}}_y,{\stackrel{.}{\mathrm{ z}}}_y}$$ are the vectors in $$ {\displaystyle R^{4_{n_n}}}$$ representing the positions and velocities of the vehicles with respect to the CoG. This function is defined on the domain D = $$ {\displaystyle R^{4_{n_n}}}$$ . The matrix L, representing a connected graph, has a single zero eigenvalue whose eigenspace is spanned by the vector. Hence the given Lyapunov function can have value zero at the non-zero state vector Z. However, this value of the state vector, physically means that all the vehicles are converged at one single point while the CoG of the system is at a point (a,b) units away from them. This is clearly impossible unless both a and b are zero. Hence the state-space for this problem, naturally excludes the eigen-space corresponding to the zero eigen- vector of the connected L matrix. Hence the Lyapunov Function chosen is positive definite. Also note that V(Z) is a discontinuous function of Z because of the discontinuity of L. Hence we have to define the generalized gradient of V(Z) as

where i = 1,2,...n_n. At point Z ∈ Ω_l and α_l=1, all other α_l = 0. Then, from Lyapunov theorem and Equations (26),

Now in the regions Z ∈ Ω_l, α_l = β_l = 1, and all other α_l = β_l = 0 and the summation in the equation simplifies to

$$ {\displaystyle \sum _{i=1}^{n_n}-c{\stackrel{.}{x}}_i^2-c{\stackrel{.}{y}}_i^2\le 0 \forall X}$$. When the corresponding αs and βs match, the summation in Equation (27) simplifies as above but at other times, its value is indefinite. However, $$ {\displaystyle \dot{\tilde{V}}}$$ is an intersection of all these sets and since we have some sets which are strictly non-positive, the intersection of all these sets is strictly non-positive. So

Therefore, the system is stable with Lyapunov theorem. ￭

We now attempt to use the discontinuous version of the LaSalle’s theorem from [10] to get a better idea of the equilibrium states of the system.

LaSalle’s Theorem: Let Γ be a compact set such that the Filippov solution to the autonomous system $$ {\displaystyle \stackrel{.}{x}=f\left(x\right)}$$ , x(0) = x₀ starting in Γ is unique and remains in Γ for all t ≥ t₀ . Let V:Γ→R be a time independent regular function Lsuch that υ ≤ 0 for all $$ {\displaystyle \upsilon \in \dot{\tilde{V}}}$$. Define $$ {\displaystyle S=\{x\in \Gamma 0\in \dot{\tilde{V}}\}}$$ . Then every trajectory in Γ converges to the largest invariant set M, in the closure of S.

Proof: See [10]. ￭

Corollary 2: The dynamic system represented by Equation (23) is asymptotically stable about its Center of Gravity, i.e. around Z = 0.

Proof: Consider the function V defined in Equation (23). This function is defined on a large enough ball Γ of R^4n_n. This can be done because as stated above the final states of the system are bounded. From Equation (28), we know that the set $$ {\displaystyle S=\{Z\mid {\stackrel{.}{z}}_x=0,{\stackrel{.}{\mathrm{ z}}}_y=0\}}$$ . The largest invariant set in S is $$ {\displaystyle M=\{Z\mid z_x=0,{\mathrm{ z}}_y=0,{\stackrel{.}{\mathrm{ z}}}_x=0,{\stackrel{.}{\mathrm{ z}}}_y=0\}}$$ . This is true because of our assumption of connectedness of the graph which implies that L has only a single zero eigen-value with corresponding eigenvector 1 and because as argued above, a and b have to be zero. Hence by applying Lasalle’s Theorem, we can conclude that all the vehicles will converge to a single point in the 2-dimensional space, which will also be its center of gravity. The CoG has been shown to be always stable and bounded above. Hence, the system is asymptotically stable around its C.G. ￭

Corollary 3: For the dynamical system in Equation (23), there exists a positive constant a independent of t₀ and a class KL function β(.,.) such that

Furthermore, this bound is of the form

Proof: The dynamical system in Equation (23) is asymptotically stable as shown above. Also, this stability is independent of t₀. Hence it is also uniformly asymptotically stable. In addition, the dynamics of the system are piecewise continuous in t and locally Lipschitz in Z. Hence, using the definition of uniform asymptotic stability from [9], Equation (18) holds. Furthermore the dynamics of the system are piecewise constant and linear. The states of the system are thus continuous, though not differentiable, exponential functions. Thus the Equation (19) holds for some k and some γ. ￭

To verify above results, let us design a force law which acts like a spring of unstretched length d attached between neighboring vehicles as described in equation.

$$ {\displaystyle f_{ix}={\Psi }_{ix}\left(X\right)-g\sum _{j\in N_i}(x_i-x_j)=gd\sum _{j\in N_i}\frac{(x_i-x_j)}{r}-g{\delta }_{x_i}}$$

$$ {\displaystyle f_{iy}={\Psi }_{iy}\left(X\right)-g\sum _{j\in N_i}(y_i-y_j)=gd\sum _{j\in N_i}\frac{(y_i-y_j)}{r}-g{\delta }_{y_i}}$$

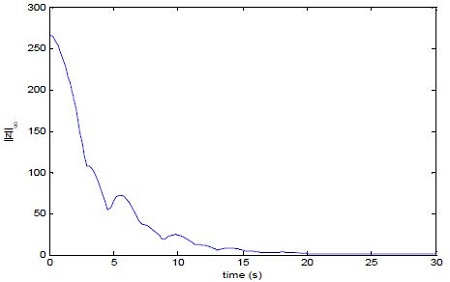
Three vehicles are initially positioned at (0,0), (300,100), (-200,300) with zero velocities. As shown in Figure 4, the state norm of the entire vehicles is maintained within a limit. The connectivity is assumed to be lost when the distance between the vehicles is larger than 400m. d is set to be 100N/m,

Figure 4:

Variation of state norm for a system with the force law

5. Conclusion

To keep the formation of a group of USVs, it is necessary to set the relationship between vehicles and forcing functions such as potential fields have been widely used in multi-agent systems. The system including the forcing mechanism is discontinuous in nature as the analysis is not limited to a constant topology. However, an assumption is made that the communication topology, while changing, remains connected at all times. Filippov’s calculus of differential equations with discontinuous right hand sides is used in the analysis. The stability analysis is then used to come up with converse Lyapunov theorems for the discontinuous system. This result is expected to be used in designing force law to deploy and keep formation for multiple surface vehicles which usually have strong nonlinearities in both system dynamics and forcing laws. Environmental forces such as hydrodyanmics terms will be incorporated to represent more realistic systems.

Acknowledgments

This work was supported by Dong-eui University Grant(2014AA461).

References

• U. S. Navy, The Navy Unmanned Surface Vehicle Master Plan, http://www.navy.mil/navydata/technology/usvmppr.pdf, Accessed October 22, 2014.
• A. Motwani, A Survey of Uninhabited Surface Vehicles, Technical Report MIDAS.SMSE.2012.TR.001, School of Marine Science and Engineering, Plymouth University, U.K, (2012).
• V. Betram, Unmanned Surface Vehicles - A Survey, Technical Report, Skibsteknisk Selskab, Copenhagen, Denmark, (2008).
• J. E. Manley, “Unmanned surface vehicles, 15 years of development,”, Proceedings of MTS/IEEE Oceans’08, p1-4, (2008). [https://doi.org/10.1109/OCEANS.2008.5152052]
• A. R. Girard, J. B. de Sousa, and J. K. Hedrick, “An overview of emerging results in networked, multi-vehicle systems,”, Proceedings of the 40th IEEE Conference on Decision and Control, p1485-1490, Orlando, Florida, (2001). [https://doi.org/10.1109/.2001.981104]
• M. Breivik, and T. Fossen, “Guidance laws for planar motion control,”, Proceedings of the 47th IEEE Conference on Decision and Control, p570-577, (2008). [https://doi.org/10.1109/CDC.2008.4739465]
• A. F. Filippov, Differential Equations with Discontinuous Righthand Sides, Kluwer Academic Publishers, Norwell, MA, (1988). [https://doi.org/10.1007/978-94-015-7793-9]
• J. Cortes, “Discontinuous dynamical systems : A tutorial on solutions, nonsmooth analysis, and stability,”, IEEE Control Systems Magazine, 28(9), p36-73, (2008). [https://doi.org/10.1109/MCS.2008.919306]
• H. Khalil, Nonlinear Systems, NJ, Prentice Hall, (1996).
• D. Shevitz, and B. Paden, “Lyapunov Stability Theory of Nonsmooth Systems”, IEEE Transactions of Automatic Control, 39(9), p1910-1914, (1994, Sept). [https://doi.org/10.1109/9.317122]