Metaheuristics for reliable server assignment problems
Copyright © The Korean Society of Marine Engineering
Previous studies of reliable server assignment considered only to assign the same cost of server, that is, homogeneous servers. In this paper, we generally deal with reliable server assignment with different server costs, i.e., heterogeneous servers. We formulate this problem as a nonlinear integer programming mathematically. Our problem is defined as determining a deployment of heterogeneous servers to maximize a measure of service availability. We propose two metaheuristic algorithms (tabu search and particle swarm optimization) for solving the problem of reliable server assignment. From the computational results, we notice that our tabu search outstandingly outperforms particle swarm optimization for all test problems. In terms of solution quality and computing time, the proposed method is recommended as a promising metaheuristic for a kind of reliability optimization problems including reliable sever assignment and e-Navigation system.
Keywords:
Reliable server assignment, Tabu search, Particle swarm optimizationNomenclature
α critical service level i.e., predetermined fraction of the operational nodes
K number of simulation replications using Crude Monte Carlo sampling to calculate CSR
n number of nodes
ci cost of deploying and maintaining a server at node i
rei , rni , rsi reliability of edge, node, and server, respectively
si binary server assignment decision variable indicating whether a server is assigned to node i ( si = 1 ) or not ( si = 0 )
C budget limit
iter number of iterations of tabu search
Stopiter the predetermined maximum number of iterations
x0 initial feasible solution
xc current solution
xbf best feasible solution found so far
xbinf best infesible solution found so far
Acronums
RSA reliable server assignment
TS tabu search
PSO particle swarm optimization
CSR critical service rate defined in Konak et al. [1]
ACO ant colony optimization
CSA clonal selection algorithm
1. Introduction
RSA problems in networks are defined as determining a deployment of servers to maximize a measure of service availability as follows.
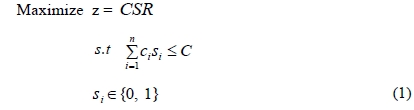
where si is the binary server assignment decision variable indicating whether a server is assigned to node i (si=1) or not (si=0). The reliability measure of CSR (critical service rate) is originally proposed by Konak et. al. [1]. They defined the CSR as the probability that more than a predetermined fraction (α) of the operational nodes have access to at least one server in case of a component failure.
The CSR is as follows:
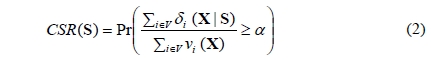
where X denotes a state vector of the network such that at least one node is operational, δi (X|S) = 1 if there exists at least one path between node i and a server node, and δi (X|S) = 0 otherwise, νi(X) = 1 if node i is operational in state X, and νi(X) = 0 otherwise. The CSR measure defined in (1) considers reachability of servers only by operational nodes because it is assumed that , when a node fails, the users of that node cannot access network services. In practice, a network continues to operate even though several of its nodes fail or become disconnected, and CSR takes into account this operational aspect of networks. The RSA problem defined in this paper is closely related with the p-median problem. The deterministic p-median problem was originally proposed by Hakimi [2]. Several authors([3]-[8]) dealt with the reliable p-median problem, which is concerned with the service unavailability due to the infrastructure disruptions or component failures. The network reliability optimization problems are known as NP-hard [9].
Melachrinoud is et al. [5] suggested a similar problem on tree networks with unreliable edges. Note that, unlike general networks as considered in this paper, on a tree network, it is computationally feasible to compute this objective function.
In the meanwhile, Eiselt et al. [10] proposed the reliable p-median problem on general networks. However, they dealt with a case of when only a single edge failure is considered at a time and extended this approach to networks with unreliable nodes. Berman et al. [11] suggested a reliable p-median on distribution networks to minimize the expected amount of satisfied demand. Nakaniwa et al. [12] considered the optimal mirror Web server assignment problem considering reliability. In this problem, edges are perfectly reliable and nodes are subject to failure. The RSA problem with the new reliability measure of CSR was solution methods by three nature-inspired metaheuristics, that is, ACO, PSO, and CSA.
However, the server cost ci was fixed to the same value of c for all servers in Konak et al. [1]. That is, they dealt with only the case of homogeneous severs. In this paper, we generally tackle the above RSA problem with the different value of ci’s for each node of server, i.e., heterogeneous servers. We also propose two metaheuristic algorithm (TS and PSO) for solving the RSA with heterogeneous servers. From computational results, we noticed that TS outstandingly outperforms PSO for all test problems.
The rest of this paper is organized as follows. Two metaheuristic algorithms for solving the RSA problem is developed in Section 2. In Section 3, we illustrate three examples of the RSA problem. In Section 4, we evaluate the performance of two proposed algorithm through the computational efforts. Finally, conclusions and future research are discussed in Section 5.
2. Solution Methods
Konak et al. [1] developed three metaheuristic algorithms for the RSA problem, that is, ACO, PSO, and CSA. In this paper, we propose an efficient TS for the RSA problem. Also we compare our TS with PSO which is the best for this problem in the literature.
2.1 TS Algorithm
The TS algorithm, first proposed by Glover [13], is a metaheuristic method to expand its search beyond local optimality using adaptive memory. The adaptive memory is a mechanism based on the tabu list of prohibited moves. The tabu list is one of the mechanism to prevent cycling and guide the search towards unexplored region of the solution space. The TS generally adopts the penalty function to allow to explore the search towards the attractive infeasible region. The TS has been successfully applied to many combinatorial optimization problems such as vehicle routing problems, travelling salesman problems, time tabling problems, and resource allocation problems, etc.
General steps of TS
The general steps of TS can be summarized as follows:
Step 0: (Initialization) Set iter=0, and initialize tabu list.
Step 1: Randomly generate the initial solution x0.
Set xc = x0 and xbf = xbinf = xc.
Step 2: a. Set iter=iter+1.
Generate the neighborhood of the current solution xc by the defined move.
b. Select the best neighborhood which is not in the tabu list. Store it as the new current solution xc. Update the tabu list.
Step 3: If xc is feasible, then go to step 4
Else go to step 5.
Step 4: If CSR (xc) > CSR (xbf) then set xbf = xc,
iter=0, and initialize the tabu list. Go to step 2.a.
Else go to step 6.
Step 5: If CSRp (xc) > CSRp (xbinf) then set xbinf = xc,
iter=0, and initialize the tabu list. Go to step 2.a.
Step 6: If iter > Stopiter, then go to step 7.
Else go to Step 2.a.
Step 7: (End) Stop with the best feasible solution found so far.
Penalty function
TS generally adopts the penalty function to allow to explore the search towards the promising infeasible region. Our TS adopts the following penalty function CSRp (see [14]) to handle the budget constraint (C).
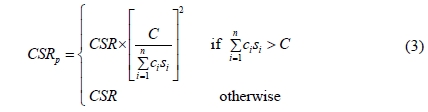
The exact computation of CSR is intractable for the size of the problem studied in this paper. Therefore, Crude Monte Carlo simulation is used to evaluate the objective function of solutions created by the metaheuristic approaches.
Defined move to generate the neighborhood
There are the following types of defined move in our TS.
i) Adding a server node to the current solution
ii) Subtracting a server node from the current solution
iii) Replacing a server node with other nodes
2.2 PSO Algorithm
PSO is a computational intelligence metaheuristic, originally developed by Kennedy and Eberthart [15][16], which was inspired by social behavior of fish schooling or bird flocking. Like evolutionary and genetic algorithms, PSO is a population-based search algorithm, i.e., it moves from a set of solutions (particle’s positions) to another set of solutions. The particles move through a D-dimensional space and each particle has a velocity that acts as an operator to obtain a new set of solutions. The particles adjust their movements depending on both their own experience and the population’s experience. At each iteration a particle moves in a direction computed from its best visited position and the best visited position of all the particles in its neighborhood. Among the several variants of PSO, the global variant considers the neighborhood as the whole population, called the swarm, which enables the global sharing of information.
The basic elements of the PSO techniques are particle, population, velocity, inertia weight, individual best, global, learning coefficients and stopping criteria. We refer interested readers to Konak et al. [1] for the detailed steps of PSO for the RSA problem.
3. Examples
3.1 Example 1
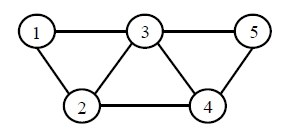
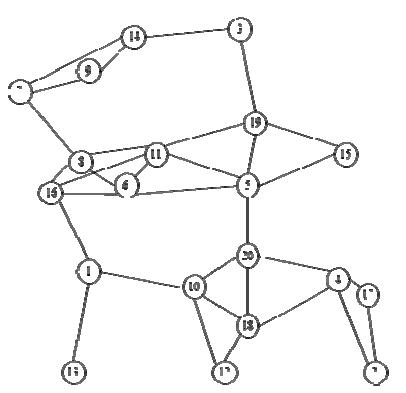
For example 1, consider the following network in Figure 1.
The input data are given by

where rei =0.8 and rni =1.0.
Our problem is as follows:
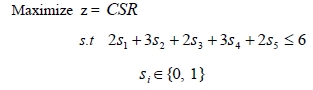
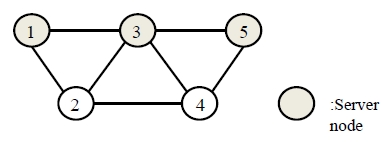
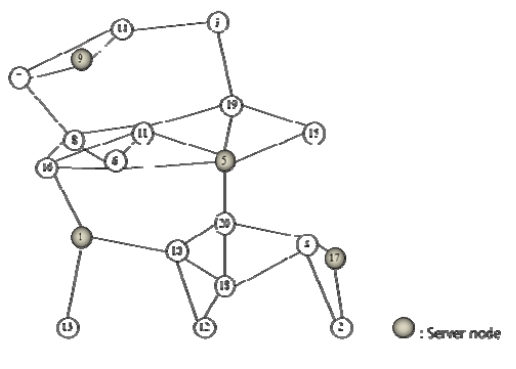
The reliability rei of each edge is 0.8. In this example, we noticed that the global optimal solution is {1, 3, 5} in Figure 2. The value of CSR is 0.95194. The value of K, α, and Stopiter are 8000, 1.0, and 5, respectively. Our TS is executed on compatible with a Pentium IV 3.0 GHz. The computing time is 0.987 seconds.
3.2 Example 2
The input data are given by

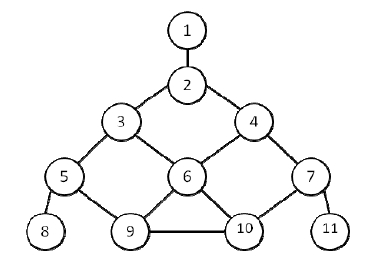
The example 2 is same to Konak et al. [1] (Figure 3).
Our problem is as follows:
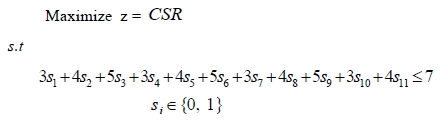
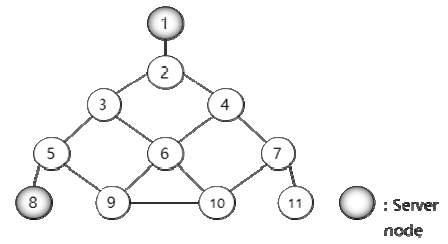
The optimal server node is {1, 8} shown in Figure 4, and the value of CSR is 0.67475. The value of K, α, and Stopiter are 8000, 1.0, and 5, respectively. The computing time is 3.735 seconds.
To evaluate the performance of our TS for the general RSA problem with different costs of deploying each server, we employed the same cost of each server for Konak et al. [1]. For example, the input data for the case of α=0.9 are given by

The global optimal solution of Konak et al. [1] is either {5, 11} or {7, 8} with the exact CSR=0.975395. We noticed that our TS finds one of the global optimum successfully.
3.3 Example 3
The example 3 was randomly generated as Figure 5. The size of node(n) is 20, and the input data are given in Table 1.
The problem is as follows :
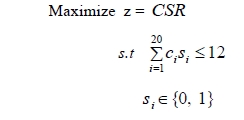
The optimal server node is {1, 5, 9, 17} shown in Figure 6, and the value of CSR, the measure of reliability, is 0.95104. The value of K, α, and Stopiter are 8000, 1.0, and 5, respectively. The computing time is 313.75 seconds.
4. Computational Results
To evaluate the performance of TS and PSO, we conducted the computational experiments for three examples of the Section 3. Each example was composed of 80 test problems, totally 240 test problems. Two algorithms (PSO and TS) were coded in C/C++ programming language, and experiments were performed on a Pentium IV 3.0 GHz PC. Performances of PSO and TS are assessed in terms of the following average relative error (A), maximum relative error (M), optimality rate (O) and average execution time (T).

In our experiments, the stopping criterion of TS was defined as 5 iterations without finding an improvement in the best feasible solution, and PSO generated 300 populations for the initial solution. Each method was applied 10 times with different starting initial solution for each test problem.
The computational results for example 1, example 2, and example 3 are summarized in Table 2, Table 3, and Table 4, respectively. From the computational results for example 1, PSO was same to TS in terms of the quality of the solution, even though the computing time of PSO was almost 6 times as much as that of TS. However, for example 2 and 3, the performance of PSO was very poor than that of TS in terms of the quality of the solution and computing time. From the computational results, we noticed that our TS outstandingly outperforms PSO for all test problems.
5. Conclusions
Konak et al. [1] originally proposed the RSA problem using the new reliability measure of CSR. They also suggested the solution methods by three nature-inspired metaheuristics, that is, ACO, PSO, and CSA. However, the server cost ci was fixed to c for all servers in Konak et al. [1]. That is, they considered only the case of homogeneous severs of the RSA problem. In this paper, we generally tackled the above RSA problem with different ci’s for each node of server, i.e., heterogeneous servers, and proposed an efficient TS for the RSA problem. Also we compared our TS with PSO, which is the best for this problem in the literature, in terms of the quality of the solution and the computing time. From the computational results, we noticed that our TS outstandingly out performs PSO for all test problems.
In terms of solution quality and the computing time, our TS is recommended as a promising metaheuristic for a kind of reliability optimization problems including the RSA problem.
To achieve a better solution quality, the development of more powerful metaheuristics and hybrid metaheuristics for the RSA problem would be performed in the future research.
Acknowledgments
This paper is extended and updated from the short version that appeared in the Proceedings of the International symposium on Marine Engineering and Technology (ISMT 2014), held at Paradise Hotel, Busan, Korea on September 17-19, 2014.
References
- A. Konak, and S. Kulturel-Konak, “Reliable sever assignment in networks using nature inspired metaheuristics”, IEEE Transactions On Reliability, 60(2), p381-393, (2011).
-
S. L. Hakimi, “Optimum locations of switching centers and absolute centers and median of graph”, Operations Research, 12(3), p450-459, (1964).
[https://doi.org/10.1287/opre.12.3.450]

- Z. Drener, “Heuristic solution methods for two location problems with unreliable facilities”, Journal of the Operational Research Society, 38(6), p509-514, (1987).
- L. D. Nel, and C. J. Colbourn, “Locating a broadcast facility in an unreliable network”, INFOR, 28(4), p363-379, (1990).
-
E. Melachrinoudis, and M. E. Helander, “A single facility location problem on a tree with unreliable edges”, Networks, 27(3), p219-237, (1996).
[https://doi.org/10.1002/(SICI)1097-0037(199605)27:3<219::AID-NET7>3.0.CO;2-L]

-
A. Nakaniwa, J. Takahashi, H. ebara, H. Okada, “Reliability-based optimal allocation of mirror servers for internet”, IEEE Global Telecommunications Conference, p1571-1577, (2000).
[https://doi.org/10.1109/GLOCOM.2000.891903]

-
L. V. Snyder, and M. S. Daskin, “Reliability models for facility location: The expected failure cost case”, Transportation Science, 39(3), p400-416, (2005).
[https://doi.org/10.1287/trsc.1040.0107]

-
H. A. Eiselt, M. Gendreau, and G. Laporte, “Location of facilities on a network subject to a single-edge failure”, Networks, 22(3), p231-246, (1992).
[https://doi.org/10.1002/net.3230220303]

-
M. Ball, “Complexity of network reliability computations”, Networks, 10(2), p153-165, (1980).
[https://doi.org/10.1002/net.3230100206]

-
H. A. Eiselt, M. Gendreau, and G. Laporte, “Optimal location of facilities on a network with an unreliable node or link”, Information Processing Letters, 58(2), p71-74, (1996).
[https://doi.org/10.1016/0020-0190(96)00024-5]

-
O. Berman, Z. Drezner, and G. O. Wesolowsky, “Locating service facilities whose reliability is distance dependent”, Computers and Operations Research, 30(11), p1683-1695, (2003).
[https://doi.org/10.1016/S0305-0548(02)00099-0]

- A. Nakaniwa, J. Takahashi, H. Ebara, and H. Okada, “Reliability-based mirroring of servers in distributed networks”, IEICE Transactions on Communications, E85-B(2), p540-549, (2002).
-
F. Glover, “Future paths for integer programming and links to artificial intelligence”, Computers and Operations Research, 13(5), p533-549, (1986).
[https://doi.org/10.1016/0305-0548(86)90048-1]

- W. C. Yeh, “A two-stage discrete PSO for the problem of multiple multi-level redundancy allocation in series systems”, Expert Systems with Applications, 36(5), p9192-9200, (2009).
- R. C. Eberhart, and J. Kennedy, “A new optimizer using particle swarwm theory”, Proceedings of the Sixth International Symposium on Micro Machine and Human Science, p39-43, (1995).
-
J. Kennedy, R. C. Eberhart, “Discrete binary version of the particle swarm algorithm”, Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, p4104-4108, (1997).
[https://doi.org/10.1109/ICSMC.1997.637339]