Effects of harmonic on battery lifetime based on variations of space vector modulation in inverter
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Various regulations for the prevention of environmental pollution are being implemented worldwide. Environmental pollution is mostly attributed to harmful gases emitted during engine combustion in ships or automobiles, including thermal power generation. To solve this problem, electricity is produced and stored from new renewable energy sources, such as solar, wind, and wave power, and is used to propel ships and cars. Electric propulsion ships or electric vehicle systems consist of a battery, an inverter, and an electric motor. The DC power stored in the battery is composed of a sinusoidal AC voltage through an inverter and is applied to the electric motor. The most important aspect is to safely manage a battery, which is a core component of an electric propulsion system, to avoid explosion, overheating or the generation of an overcurrent. Therefore, it is important not only to always observe the ambient temperature, rated voltage, and current but also to remove factors that may harm the safety of the battery in advance. In particular, the sinusoidal AC voltage applied to the motor modulates the command voltage into the form of a switching pulse, which is then applied to the upper and lower legs (Leg) of the inverter. Therefore, the voltage and current of the inverter contain various harmonics that can adversely affect the propulsion system, including the batteries. In this study, the modulation types of the two switching pulses are selected, and motor-speed control is performed according to each type. Simultaneously, the relationship between the harmonics and lifetime is analyzed by measuring the current harmonics flowing through an electrical motor and the internal resistance, which is a parameter that can predict the lifetime of the battery.
Keywords:
Pollution, Battery, Inverter, Harmonics, Battery Internal Resistance (IR)1. Introduction
The world has entered the 20th century, when fossil fuels are increasingly depleted and means of transport are switching to electricity from gasoline or diesel oils. Electric vehicles (EVs) are becoming an increasingly popular mode of transportation as the world moves towards a more sustainable and eco-friendly future [1].
Unlike traditional gasoline-powered vehicles, EVs rely on batteries to power their motors. This implies that they produce zero emissions, which can help reduce air pollution and greenhouse gas emissions [2]. In recent years, EV technology has made significant progress, and the range and performance of electric cars have improved dramatically. With governments around the world offering incentives to encourage the adoption of EVs and major automakers investing heavily in technology, the future of transportation appears to be electric.
In an electrical vehicle, the inverter and battery are two essential components. The inverter includes a motor control circuit and an electrical motor. To control an electric motor with high performance, many researchers have improved and proposed motor control methods such as the space-vector pulse width modulation (SVPWM) [3], third harmonic injection PWM (THIPWM) [4], and discontinuous PWM (DPWM) [5]. When the motor is operated with each of these control methods, different results are obtained in terms of the advantages in dynamics and the disadvantages in the noise of each of these methods. The dynamic advantages are the stability of the torque and speed. However, one disadvantage is the creation of different levels of current harmonics in the connected circuit. In general, it is known that the current harmonic affects not only the electrical components in the circuit but also the battery lifetime, temperature, and chemical reactions [6][7].
Manufacturers and customers always expect the battery lifetime to be optimized and the battery aging time to be performed as slowly as possible. Therefore, this study analyzed the battery lifetime and aging speed according to different PWM methods based on space vector modulation, which influences the motor current harmonic characteristics. Here, the two switching modulation methods are symmetric and asymmetric switching methods; the reason for using these methods is that the phase voltage is in the form of a pulse in the symmetric method and appears in the form of a square wave in the asymmetric method and can be useful for comparing or analyzing harmonic characteristics.
2. Theory
2.1 Harmonic and Total Harmonic Distortion (THD)
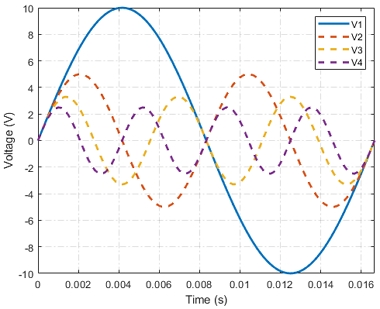
Harmonic electricity is a wave of current or voltage with frequencies that are multiples of the fundamental frequency. In some countries, the regulated fundamental frequency can be 50 Hz or 60 Hz. If the fundamental frequency is 50 Hz, the second harmonic is 100 Hz, and the third harmonic is 150 Hz. Typical harmonic waves are shown in Figure 1 with a fundamental wave. The state of harmonics can be expressed using many methods, but usually through the Total Harmonic Distortion (THD) parameters.
Fundamental wave and harmonics
THD is a measure of harmonic distortion in a signal and is defined as the total power ratio of all harmonic components to the power of the fundamental frequency. THD provides information on stability and evaluates the quality of an electrical system.
The THD helps determine the degree of distortion owing to triangular, square, and sawtooth waves mixed in the shape of a desirable sine wave. Harmonics only provide energy sources, and the components produce any frequency. When the THD factor was minimized, the system output exhibited less noise or distortion. Thus, the THD must be maintained as low as possible.
THD(%) was calculated using the following Equation (1) [8]:
| (1) |
V1, V2 ~ Vn are the root-mean-square magnitudes of each harmonic from the fundamental wave and n is the harmonic number. V1 is the magnitude of the fundamental wave.
Undesirable harmonics exist in nonlinear loads, which consist of power conversion devices such as variable frequency drivers (VFD), UPSs, rectifiers, and motor generators, and occur during the energy conversion process.
This paper presents the variation in the magnitude of THD by changing the PWM methods used in vector control modulation. We can consider the effect of the harmonic components on the power current when operating a variable-frequency driver to control a three-phase motor.
2.2 Internal Resistance Estimation of Battery Utilizing Open Circuit Voltage (OCV)
In a battery management system, SOC estimation is important for analyzing the internal resistance of the battery. Internal resistance is one of the main causes of aging and affects the battery lifetime. Many methods are used for the estimation, such as the Coulomb counting method (CCM), model-based estimator, and open circuit voltage (OCV) [9]. In the CCM, the SOC is given by the remaining available capacity. However, using the offline OCV method, the exact SOC data obtained consist of the internal resistor in the battery. Therefore, an offline OCV method was used in this study. The OCV of a battery is the electrical disproportion between the positive and negative terminals when the battery is disconnected from any load. This implies that no current flows between the two terminals of the battery. Therefore, the OCV can be analyzed using Randles' primary battery model [10].
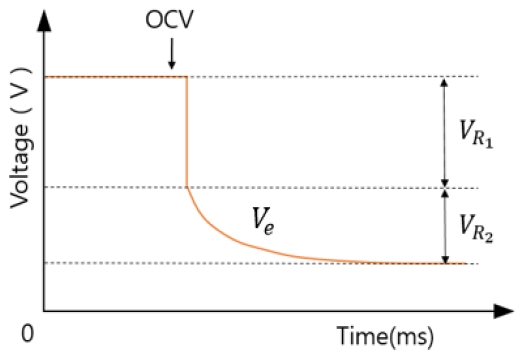
The Randles primary battery model is expressed in Figure 2. Figure 3 shows a graph of the battery terminal voltage when the battery performs a charge/discharge current.
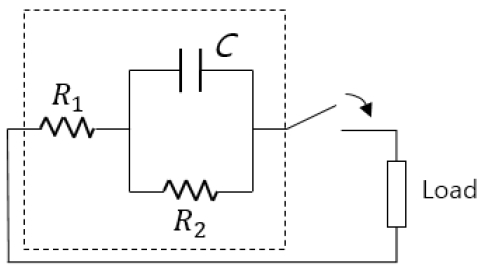
Equivalent circuit of Randles model and loadR1: Battery IRR2: Ionization loss resistanceC: Double-layer capacitance
Estimation of battery resistance R1 and R2VR1= R1 IVR2= R2 I(2)Ve=R2exp-1R2Ct
The Randles’ primary battery model is illustrated in Figure 2. A battery is represented by a resistor R1 (IR) and serially connects to a circuit consisting of capacitor C that is parallel to another resistor R2.
Figure 3 shows the battery voltage state when the battery is connected to an electronic load and discharged at a constant current, as represented by Equation (2). When the battery was connected to an electronic load, the double-layer capacitance is shorted, resulting in an R2 of zero.
Therefore, the float voltage of the battery momentarily drops to the VR2 value, the internal resistance (IR) is calculated by dividing the voltage drop VR1 by the load current 1A, and the life of the battery is checked by measuring the change in IR after the load experiment [11][12].
3. Experiment and Consideration
3.1 System Configuration
Figure 4 shows a typical configuration of the electric vehicle. Through Figure 4, the battery provides power to the inverter to control the three-phase motor. The IR of the battery is estimated using the OCV technique. This value can be used to determine the change in the IR of the battery and predict the degree of degradation and lifetime.
Diagram of electrical propulsion system
A device was used to measure the THD during the discharge process of the EV motor. Thus, the THD can be easily confirmed to compare and check how the harmonics affect the IR and battery lifetimes.
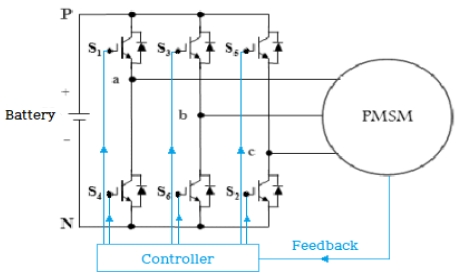
The inverter consists of a microcontroller (MCU), gate driver, and feedback system as current and speed sensors. The three-phase inverter control method is the PMSM Vector Control Technique. Typically, the method utilized is a Voltage Vector Control technology based on PMSM vector control techniques to convert DC into AC [13]. The operating status includes eight switching states for generating voltage space vectors based on the space vector in a three-phase two-level inverter.
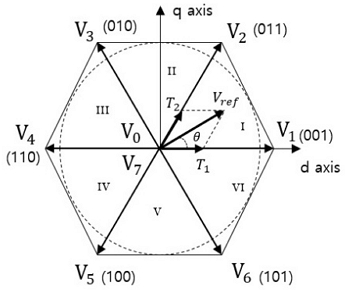
The output voltages of the eight switching states of the inverter are presented as a vector diagram, and a regular hexagon is formed, as shown in Figure 5, From the voltage vector V(1) to V(6), the maximum output of the inverter is at the top of the hexagon. Any voltage output Vout in the hexagon can be calculated using three stationary vectors corresponding to the side of the triangle divided by the hexagon and one zero vector. The dwell times for any stationary vector are the duty cycle times of the selected switches during the sampling period TS. Hence, the duty cycle time of the chosen switches can be determined using Equation (3), (4), and (5).
| (3) |
| (4) |
| (5) |
- Vref : Reference voltage
- Vd : DC voltage
- Ts : Sampling period
Block diagram of space vector
With the calculated dwell time and space vectors selected, the table of the switching times for Vref was presented as Table 1 and Table 2.
Three-phase symmetrical modulation switching time of Sector 1
Three - phase asymmetrical modulation switching time of Sector 1
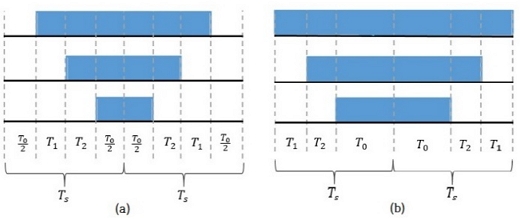
Table 1 lists the switching times for Vref with three-phase symmetrical modulation. Table 2 lists the switching times for Vref with three-phase asymmetrical modulation. The switching sequence for Vref with the three-phase symmetrical modulation of sector 1 is illustrated in Figure 6 (a). The switching sequence for Vref with the three-phase asymmetrical modulation of Sector 1 is shown in Figure 6(b) [14].
Pulse width of Sector 1 in (a) symmetrical modulation and (b) asymmetrical modulation
3.2 Experiment
The experimental device includes a 4-pack li-ion battery, microcontroller, switching gate drive, three-phase inverter circuit with a permanent magnet synchronous motor (PMSM), current sensors, and voltage sensors, as shown in Figure 7. The three-phase inverter consists of six IGBTs and takes on the role of converting the DC voltage of the 4-pack li-ion battery into AC output voltage to supply electric power for the PMSM. Switching the IGBTs PWM pulses to the output of the microcontroller was amplified through isolated gate drivers. The PWM pulses were generated using the two types of space vector algorithms proposed in Section 3.1.
Experimental devices
The module was controlled by interfacing it with a computer through the Sync works JTAG emulator (XDS 300S). The Li-ion battery pack consisted of four batteries connected in series, and the battery voltage and current were measured using an oscilloscope. The harmonic level was analyzed by collecting the parameter data of the output current using MATLAB Simulink. The lithium-ion battery pack characteristics are listed in Table 3.
Lithium-ion battery characteristics
To perform the discharging operation test for the battery, a 14.8 V, 2,600 mAh module composed of four batteries was utilized. The battery pack was discharged continuously for 360 min, and an electron load was applied after discharge to measure the IR of the battery through the instantaneous discharge of 1 A constant current. For the discharge operation test, the PMSM connected to a three-phase inverter was rotated under no-load conditions. The three–phase inverter was set to operate commonly with 4.85 to 4.9 watts in all the proposed methods.
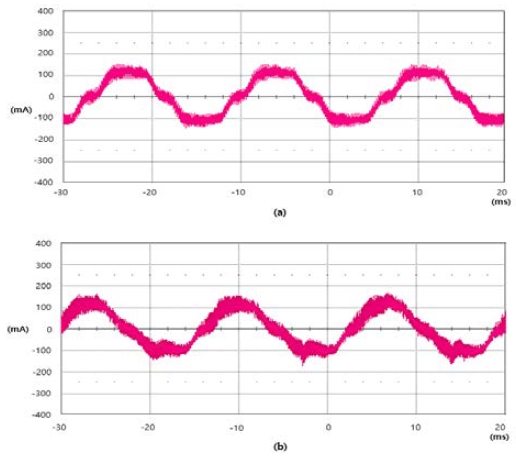
Figure 8 shows the phase current measured at the motor terminal. Figure 8 (a) shows the measured phase current of the motor when operated with symmetrical modulation. Figure 8 (b) shows the measured phase current of the motor in the asymmetrical modulation. The phase current of the motor created by the asymmetrical modulation was distorted and included sharper noise current peaks than the phase current of the motor when operating with symmetrical modulation.
Output AC current of inverter with (a) symmetrical modulation and (b) asymmetrical modulation
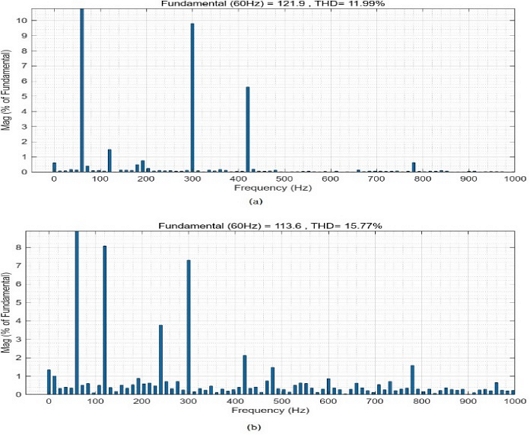
When the motor was driven with symmetrical modulation, the measured total value of the harmonic flowing through the motor was 11.99% as shown in Figure 9 (a). However, when the motor was driven with asymmetrical modulation, the measured total values of the harmonic increased highly in the range of 15.77%, as shown in Figure 9 (b). It was found that the current harmonics varied depending on the PWM method. Generally, The asymmetric method is known to have a relatively large number of low-order harmonics due to the reduced switching frequency, as the phase voltage waveform has a square wave shape compared to the symmetric method.
Output AC current THD% of inverter with (a) symmetrical modulation and (b) asymmetrical modulation
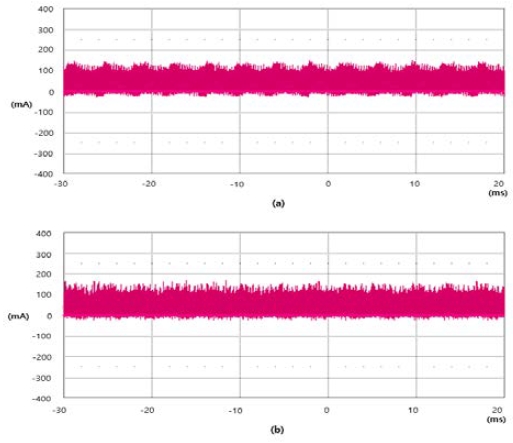
Figures 10 (a) and (b) show the output DC of the battery at the front end of the inverter. Figure 10 (a) shows the symmetric modulation, Figure 10 (b) shows the asymmetric modulation, and the harmonic modulation is larger in asymmetric modulation. The switching noise at the inverter power end affected the input side, thereby affecting the internal resistance of the battery.
DC current in the inverter input with (a) symmetrical modulation and (b) asymmetrical modulation
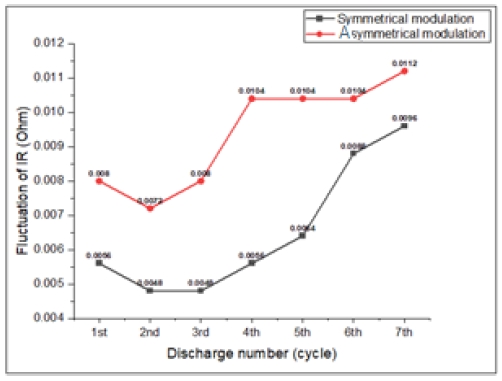
Figure 11 shows a graph measuring the changes in the internal resistance of the battery before and after operation and performing symmetric and asymmetric modulation switching control of the inverter.
IR fluctuation of the battery according to symmetrical and asymmetrical modulation
The driving time was 360 min, and seven operations were performed. The graph shows that in comparison with the symmetric modulation method, the asymmetric switching control increases the change in the internal resistance of the battery.
The average value of the internal resistance change during symmetric modulation is 0.00937 ohms, and 0.00651 ohms for asymmetric modulation; the difference between the two values is 0.00286 ohms. This phenomenon is considered to have degraded the integrity of the battery owing to the harmonic distortion of the inverter input.
4. Conclusion
In this study, an electric vehicle propulsion system connected by a battery, inverter, electric motor, and microprocessor was constructed, and the switching pattern of an inverter driving a permanent magnet synchronous motor was symmetrically and asymmetrically applied to analyze the harmonics, battery internal resistance, and lifetime characteristics.
Both methods operated at 4.85 to 4.9 watts, and the following conclusions were obtained.
- (1) Harmonic currents flowing through an electric motor (or battery) when operating with symmetric switching pulse inputs and asymmetric switching pulse inputs were observed to be 11.99% and 15.77%, respectively. It was found that higher harmonics existed when operating in the asymmetric mode.
- (2) After repeating battery charging and discharging for 7 cycles, the internal resistance of the battery was measured, and as a result, the average value of the internal resistance change during symmetric modulation was 0.00937 Ohm and 0.00651 Ohm; the difference between these two values was 0.00286 Ohm.
Author Contributions
Conceptualization, S. G. Lee; Methodology, S. G. Lee and K. K. Yoon; Software, V. V. Hung; Formal Analysis, V. V. Hung; Investigation, K. K. Yoon; Re-sources, V. V. Hung; Data Curation S. G. Lee; Writing-Original Draft Preparation, V. V. Hung and S. G. Lee; Writing-Review & Editing, K. K. Yoon; Visualization, V. V. Hung; Supervision, K. K. Yoon; Project Administration, S. G. Lee; Funding Acquisition, K. K. Yoon.
References
-
H. -K. Ku, H. -R. Seo, and J. -M. Kim, “Lithium-ion battery energy storage system for power quality improvement in electrical propulsion ships,” The Transactions of the Korean Institute of Power Electronics, vol. 20, no. 4, pp. 351-355, 2015 (in Korean).
[https://doi.org/10.6113/TKPE.2015.20.4.351]
-
C. Cunanan, M. Tran, Y. Lee, S. Kwok, V. Leung, and M. Fowler, “A review of heavy-duty vehicle powertrain technologies: Diesel engine vehicles, battery electric vehicles, and hydrogen fuel cell electric vehicles,” Clean Technologies, vol. 3, no. 2, pp. 474-489, 2021.
[https://doi.org/10.3390/cleantechnol3020028]
- W. F. Zhang and Y. H. Yu, “Comparison of three SVPWM strategies,” Journal of Electronic Science and Technology, vol. 5, no. 3, pp. 283-287, 2007.
-
J. Jose, G. N. Goyal, and M. V. Aware, “Improved inverter utilisation using third harmonic injection,” 2010 Joint International Conference on Power Electronics, Drives, and Energy Systems & 2010 Power India, pp. 1-6, 2010.
[https://doi.org/10.1109/PEDES.2010.5712490]
-
A. M. Hava, R. J. Kerkman, and T. A. Lipo, “A high-performance generalized discontinuous PWM algorithm,” IEEE Transactions on Industry applications, vol. 34, no. 5, pp. 1059-1071, 1988.
[https://doi.org/10.1109/28.720446]
-
R. F. Nelson and M. A. Kepros, “AC ripple effects on VRLA batteries in float applications,” Fourteenth Annual Battery Conference on Applications and Advances, Proceedings of the Conference (Cat. No. 99TH8371), pp. 281-289, 1999.
[https://doi.org/10.1109/BCAA.1999.796005]
- E. N. Power, “Effects of ac ripple current on VRLA battery life,” A Tech. Note from Expert. Business-Critical Contin, 2015.
-
L. Alhafadhi and J. The, “Advances in reduction of total harmonic distortion in solar photovoltaic systems: A literature review,” International Journal of Energy Research, vol. 44, no. 4, pp. 2455-2470, 2019.
[https://doi.org/10.1002/er.5075]
-
L. Sun, G. Li, and F. You, “Combined internal resistance and state-of-charge estimation of lithium-ion battery based on extended state observer,” Renewable and Sustainable Energy Reviews, vol. 131, 2020.
[https://doi.org/10.1016/j.rser.2020.109994]
-
J. E. B. Randles, “Kinetics of rapid electrode reactions,” Discussions of the Faraday Society, vol. 1, pp. 11-19, 1947.
[https://doi.org/10.1039/df9470100011]
- D. Y. Noh, I. S. Hwang, and J. -Y. Yoo, “SOH estimation method of lithium polymer batteries using OCV,” Proceedings of the KIPE Conference, The Korean Institute of Power Electronics, pp. 269-270, 2010 (in Korean).
-
J. L. Choi and S. -G. Lee, “High safety battery management system of DC power source for hybrid vessel, " Journal of the Korean Society of Marine Engineering, vol. 40, no. 7, pp. 635-641, 2016 (in Korean).
[https://doi.org/10.5916/jkosme.2016.40.7.635]
-
S. K. Dwivedi, M. Laursen, and S. Hansen, “Voltage vector based control for PMSM in industry applications,” 2010 IEEE International Symposium on Industrial Electronics, pp. 3845-3850, 2010.
[https://doi.org/10.1109/ISIE.2010.5637742]
-
D. Holmes and T. A. Lipo, Pulse Width Modulation for Power Converters: Principles and Practice, vol. 18, John Wiley & Sons, 2003.
[https://doi.org/10.1109/9780470546284]