Simplified prediction strategies for real-time predictive control of magnetic levitation systems
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
A simplified real-time state and cost prediction strategy is presented for the constrained predictive control of position in magnetic levitation systems which are characterized by fast and highly nonlinear dynamics. The proposed control scheme uses a transformation of the input variable to feedback linearize the system and includes an accompanying control implementation strategy allowing an accurate prediction of future states and outputs over relatively large time horizons. Further, to deal with the resulting non-convex constraint on the control input, the scheme employs a reformulation of the corresponding online optimization problem with a semidefinite-relaxation-based convexification procedure leading to a simplified online optimization problem. The resulting predictive control strategy does not necessitate a very small sampling interval for accuracy and can be used to optimize the constrained evolution of the magnetic object’s position over a desired time horizon. Realistic nonlinear simulations show that the proposed scheme is effective and is able to achieve the desired control objectives.
Keywords:
Real-time predictive control, Nonlinear MPC, Magnetic levitation systems, Input transformation, Constrained control1. Introduction
Real-time optimization-based control, widely known as model predictive control (MPC), has, over the years, evolved as a suc-cessful optimal control approach for a variety of multivariable dynamical systems [1]. Its ability to handle complex, multivaria-ble systems with constrains in inputs and outputs comes from its strategy of computing, during each sampling interval, the se-quence of control inputs over a finite time horizon by solving an optimization problem based on a discrete-time (DT) model of the system. Originally popular in the process industries for the con-strained control of slow processes, which allow enough time to solve an optimization problem within each sampling interval [2], thanks to the advancements in computing speed, it is increasingly being successfully used, in its various forms [3]-[5], for control applications in most areas including those involving fast process-es (e.g., [6]-[7]).
The need to be able to solve a constrained optimization prob-lem in real time makes MPC computationally challenging, partic-ularly in situations involving nonlinear or/and uncertain systems with fast dynamics. For a nonlinear system, the corresponding DT system model is typically approximated for a small sampling period and the resulting MPC problem is a non-convex optimiza-tion problem over a large sequence of input variables. The prob-lem of reducing the online computational burden of nonlinear MPC has been extensively researched and the efforts have led to various computationally efficient approaches involving strategies such as gain scheduling [8], advanced-step computing [9], for-mulating the problem as a robust problem [10], using offline optimized, dynamically evolving control moves [11] and so on. Most alternative strategies simplify online computations with some compromise on the accuracy of the system model used for predictions and hence on the optimality of the solutions. Appro-priate MPC control strategies for nonlinear systems are largely subjective, depending on the nature of the nonlinearities and the control objectives.
In this paper, we explore strategies for an appropriate DT dy-namics modeling and a simplified but accurate prediction of the future state and output trajectories for predictive control of mag-netic levitation systems which are marked by fast and highly nonlinear dynamics. Magnetic levitation systems or suspension systems involve the levitation of an object of magnetic material using an electromagnetic mechanism and these systems enable contactless and noise free operation in many motion-related ap-plications in areas such as rail transportation (high speed trains), energy storage systems, robotics, photo-lithography, contactless bearings, heart pumps wind turbines and so on [12]-[18]. While contactless operations using magnetic levitation systems are pref-erable over other alternatives, the challenges that these systems pose for the designer in the area of precise modeling, sensing and control are also significant.
For the precise position control in a magnetic levitation system, several control strategies have been explored in the past several years and the problem is actively being researched. Dynamic feedback linearization, linear quadratic control, adaptive control, sliding mode control, robust control, H∞-control and μ-synthesis are some of the approaches proposed for this purpose in specific applications [14], [18]-[25]. Since the problem in-volves precise control requirements and constraints, MPC is also a promising control approach for this problem. Various MPC strategies that have been explored for this problem include stand-ard finite-horizon MPC [26], LMI-based robust MPC [27]-[28], nonlinear MPC [29], disturbance observer- based MPC [30], linear MPC over feedback linearized dynamics [31], deep-learning-based MPC [32] and so on.
Because of fast nonlinear dynamics of the system, most MPC strategies for magnetic levitation systems use a prediction over a small time horizon, using very small sampling intervals and up-dating the control input at a high frequency, usually using the strategy to compensate for disturbance inputs and load changes. Using a real-time optimization over a larger time horizon is com-putationally demanding. This may prevent the MPC strategy from achieving its objective of achieving some kind of optimality over a certain time horizon. To address this issue, this paper is aimed at having a linear prediction model with an implementation strategy that significantly reduces the prediction inaccuracies associated with linearized models. For this, we consider a simple transformation of the input variable in the form of a simple feed-back linearization that leads to a linear prediction model. Howev-er, the transformation results in a set of nonlinear, non-convex constraints, and to deal with this problem, we propose a sem-idefinite relaxation for convexifying the constraints and thus formulate the MPC problem as a semidefinite programming (SDP) problem. While this convex formulation of the problem reduces the complexity of online computations associated with nonlinear MPC allowing us to make predictions over longer time horizons using piecewise constant control inputs over chosen sampling periods, accurate deterministic predictions also enable us to avoid the conservatism associated with robust approaches. The effectiveness of the proposed scheme is assessed with realis-tic nonlinear simulations involving various aspects of the control problem.
2. Background and Preliminaries
2.1 Nonlinear MPC
Consider a dynamical system described by the state and output equations
| (1a) |
| (1b) |
where is the system state, is the control input and is the controlled output at time t, and fc(., .) and h(.) are possibly nonlinear algebraic functions. The MPC approach aims to drive the output y(t) of the system to a chosen reference value r by computing, and applying the control input u(t) such that it minimizes a suitable cost function over a finite time horizon. A typical cost function considered for minimization in real time is a quadratic cost function of the form.
| (2) |
where Qc is a positive semidefinite matrix, Rc is a positive definite matrix, lc(.) is a positive semidefinite function defining the terminal cost, t0 is the initial time, tf is the final time, and is an operating point of the system such that
The state x(t) and the input u(t) are usually required to satisfy certain constraints which may be expressed as and where and are convex sets.
Since the MPC approach envisages a real-time solution of the optimization problem, in practice, a DT approximation of the problem is considered choosing a suitable sampling period, T and the problem is solved every time step. Typically, the system dynamics in (1) are approximated by a DT description
| (3) |
where denotes the discrete time step 0, 1, 2, …, x(k) = x(kT) and y(k) = y(kT) denote the values of the state and the output at the beginning of the time step k, u(k) gives the control input to be applied during time step k, and f(., .) is the equivalent or approximate state-update function. Further, assuming a uniform sampling, the cost function in (2) is approximated by a predicted cost function of the form
| (4) |
where Q and R are appropriately defined positive (semi) definite matrices, l(.) is a positive semidefinite function used to specify the terminal cost and N is the horizon length. The subscript k + i|k attached to a variable indicates the value of the variable at time k + i predicted at time k.
The finite-horizon MPC optimization problem can be stated as
| (5a) |
subject to the constraints
| (5b) |
The basic steps in an MPC scheme based on problem (5) are summarized in Figure 1.
If the system is a linear time-invariant system, the DT state equation in (3) can be obtained exactly, typically assuming a zero-order hold at the input, i.e., assuming u(t) = u(k) for kT ≤ t < (k+1)T. Then, if the terminal cost l(.) is a convex quadratic function, problem (5) can be formulated as a convex quadratic programming (QP) problem and solved efficiently. For a general nonlinear system, however, problem (5) is often a challenging problem, particularly for systems with fast dynamics. On the one hand, an exact DT model of system dynamics is usually not easy to obtain, and approximate models lead to inaccurate multi-step predictions of states. On the other hand, even with a relatively more accurate DT model, the state update equation is typically nonlinear and results in a non-convex optimization problem which is difficult to solve in real time except in cases with small horizon lengths.
2.2 Magnetic Levitation Systems
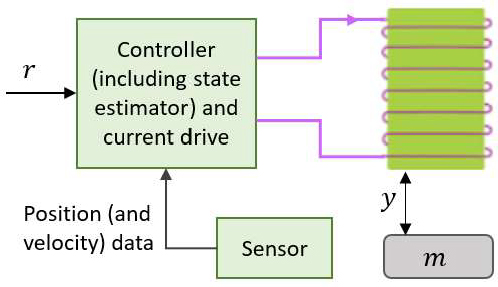
A magnetic levitation system comprises an object of magnetic material which is suspended in the air under the effect of an electromagnetic field created by a current-carrying coil. A schematic of the system is shown in Figure 2 where the vertical displacement of the object, y, increases as it moves downwards from the top. By varying the current in the coil, the vertical position of the object can be varied. Given the desired vertical position, r, the controller and the current drive generate the necessary current in the coil, based on the measured actual position (and speed) of the object obtained from the sensor (which is typically an optical sensor), to move the object to the desired position.
Nominally, the motion of the object is described by the differential equation
where m is the mass of the object, κ is the relevant coefficient of viscous friction and g is the acceleration due to gravity. Fm (y, i) is the position-dependent force on the magnetic object due to the current in the coil and is given by
where L and a are relevant constants (see, e.g., [33, pp. 31-32]).
Defining x1 = y and as state variables and u = i as the input, the corresponding state-space description of the system can be expressed as
| (6) |
The state variables and the control input are typically required to satisfy the constraints
| (7a) |
| (7b) |
A steady-state operating point of (6) has the form
To formulate a reference-tracking MPC problem of the form (5) for system (6) under the constraints in (7), a DT approximation of the state equation in (6) is needed. One can either use the DT equivalent of the state equation in (6) linearized about the operat-ing point associated with the reference point or a nonlinear DT approximation of the state equation in (6) for a small sampling period by using the simple Euler or some Runge-Kutta (RK) method.
While the use of a linearized model results in a QP-based MPC optimization problem, the approximation involved in the linearization leads to prediction errors for initial states not close to the operating point. The use of some approximate discretization, on the other hand, results in a nonlinear DT system model and hence a non-convex MPC optimization problem with a large horizon length, which can be computationally demanding. In the sequel, we explore an alternative approach to formulate the pre-dictive control problem for system (6) with a linear DT approxi-mation of the continuous-time state equation based on a trans-formation of the input variable.
3. Simplified Prediction Strategies for Real-time Nonlinear Predictive Control
3.1 Discretization of the System Model
Define a new variable
and rewrite system (6) as
| (8) |
where and . The state equation in (8) is linear in the transformed input variable v. This transformation, however, has implications on the discretization of the model, on the form of the constraints and the cost function, and on the implementation of the control inputs.
Assuming a constant v throughout the sampling interval T, the DT counterpart of (8) is given by
| (9) |
where and .
The assumption of a constant v throughout the sampling period in this DT model means that the actual control input u to be applied to the system is a function of the value of y(t) within the period. This has implications on the control implementation which we shall discuss in the sequel.
Lemma 1: Given a constant v, let the control input u(t) in (6) for any time be defined as
| (10) |
where and . Then, the state of system (6) at time t0+T is
Proof: This result can be easily seen with some algebraic exercise. With v defined as u2 / (a + x1)2, the second component of the state equation in (6) can be written as
Assuming a constant v(t) = v for t from t0 to t0 + T, we have,
The first component of the state derivative in (6) can be ex-pressed as
The value of x1(t) for any is given by
Hence, with u(t) defined as in Equation (10), v(t) is constant and equal to v and hence the value of x(t0 + T) directly follows from the DT equivalent (9) of model (8).
Lemma 1 shows that if the control input u(t) given by Equation (10) is implemented for with v = v(k) for each t0 = kT, k = 0, 1, 2, …, then the controlled system is exactly described by the DT LTI system model (9). So, under this assumption, we can use model (9) to predict future states of the system.
3.2 Constraints and the Cost Function
Using (9) as the model of the system, we can easily express the sequence of the future states of the system at the sampling instants. Defining the vectors
we can express x(k) as (see, e.g. [2])
where
and c = . Here, Inx denotes an identity matrix of size nx.
Constraints on state variables in (7a) can be imposed at the sampling instants and are collectively expressed as a linear con-straint
| (11) |
where Mx and Mv are appropriately defined matrices. The constraint on the input variable u, expressed in terms of v, is, however, more complicated. Like y(t), for a constant v(k), u(t) varies within the sampling period and we can impose the constraint on it at the sampling instants, i.e.,
| (12) |
for i = 0, 1, …, N - 1. While the left-hand side constraints in (12) are equivalent to
| (13) |
the right-hand side constraints are nonlinear and non-convex. Define constant matrices
where blkdiag(Δ1, Δ2) denotes a block diagonal matrix with diagonal blocks Δ1 and Δ2, and ⊗ denotes the Kronecker product. Further, defining a new matrix variable
| (14) |
the constraints in (12) can be equivalently expressed as a pair of linear matrix inequality (LMI) constraints on v(k) and V(k) as
| (15) |
where diag(v) for a vector v represents the diagonal matrix with the elements of v along its diagonal and diag(Δ) for a square matrix Δ represents a diagonal matrix containing the diagonal elements of Δ. Further, and a = a1N, where 1N denotes an N-dimensional vector with all 1’s. Matrix elements marked * in (15) complete the symmetric matrices.
Next, we consider a cost function of the form (4) with Q > 0, a small R ≥ 0 and l(ϕ) = ϕT P ϕ where P ≥ 0. This cost function can be written as
where with and . Further, omitting the constant terms, we can write J(k) as
| (16) |
The MPC optimization problem can now be stated as the minimization of the cost J(k) in Equation (16) under constraints (11), (14) and (15). Condition (14), however, is a nonconvex equality constraint and is computationally difficult to handle. For the particular form of the cost function that we have, a potential alternative is to convexify it by replacing it with its semidefinite relaxation (see, e.g., [34]) given below:
| (17) |
For the equality constraint (14) to be satisfied, the relaxed condition (17) should hold tightly.
Lemma 2: If the minimization of the cost function J(k) in (16) under constraints (11), (15) and (17) results in an optimal solution such that the relaxed constraint (17) is tight (i.e., condition (14) holds), then then nonlinear constrains in (12) are satisfied by the predicted input and state sequences at all sampling instants.
Proof: It is easy to see that the first set conditions in (12) can be equivalently written as
This can be expressed in vector form as
where ∘ denotes the Hadamard (elementwise) product and the squaring on the left side is to be understood in the elementwise sense. With the assumption that equality (14) holds true, this condition can be written as
which is equivalent to the first LMI in (15). Similarly, the second set of conditions in (12) can be equivalently expressed as the second LMI in (15). Hence, the lemma follows.
Remark 1: In the problem that we have, matrix and vector c have all positive elements and has negative elements. The upper limit constraint on the control input becomes active when x1(k) is larger than and the difference between them is significant. Under this situation, the minimization of cost J(k) in Equation (16) typically results in a solution for which the relaxed condition (17) is tight.
3.3 Terminal Constraint and Stability
In order to ensure that the output of the controlled system un-der the control scheme based on the minimization of the MPC cost in Equation (16) accurately tracks the desired position, we introduce a terminal constraint in the MPC problem. The terminal constraint set is based on a carefully chosen terminal controller. An offline-optimized dynamic terminal controller such as the one discussed in [11] can offer a larger terminal set which reduces the online computational burden. In this work, however, we consider the standard static feedback terminal control law
| (18) |
where , and K is the optimal state-feedback gain that minimizes an infinite-horizon linear quadratic cost, typically obtained as
| (19a) |
where P is the solution to the well-known algebraic Riccati equation and also satisfies the Lyapunov equation
| (19b) |
so that the infinite horizon terminal cost is represented by l(ϕ) = ϕT P ϕ.
The corresponding terminal constraint set that is computed should be invariant and constraint-admissible for the terminal controlled system, i.e., for a state of the terminal controlled system starting in this set, the system constraints should be satisfied at all future times. Since the control law also depends on , i.e., on , for terminal set computations, we consider an augmented state , which follows the dynamics
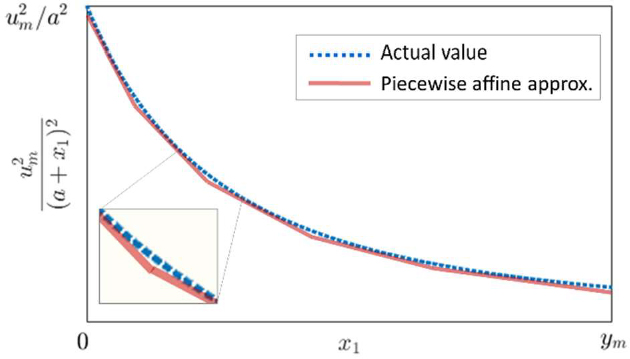
| (20) |
where we have used the fact that Further, since the upper bound on the transformed input variable v, viz., is dependent on the state of the system in a nonlinear way, we consider a piecewise affine approximation of this upper bound for a number of segments of as illustrated in Figure 3. We then compute a constraint-admissible invariant set for the state of system (20) for in each of these segments while allowing x1 to extend beyond the segment under the affine approximation of the upper bound for v for this segment. Let be the nonoverlapping segments considered in and, for each segment i, let be the constraint-admissible, invariant set for z(k), satisfying
| (21) |
obtained for and in some under the linearized constraint for this section. Note that with the linearized state-dependent bound, the constraints on v(k) can be expressed as linear constraints for each segment and the corresponding invariant set can be obtained using an iterative algorithm (see, e.g., [35]).
The MPC optimization problem including the terminal con-straint based on the simplified prediction strategy for the magnet-ic levitation system can be stated as
| (22a) |
with J(k) defined in Equation (16), subject to the constraints (11), (15), (17) and
| (22b) |
where is such that . The MPC scheme based on problem (22) is summarized in Figure 4.
Proposition 3: With the off-line computations carried out as outlined in the scheme of Figure 4, if the MPC optimization problem (22) is feasible for the initial state x(0) at time k = 0, and providing that the constraint (17) holds tightly at every step k ≥ 0, the online steps outlined in the scheme of Figure 4 ensure that (a) the problem remains feasible at all time steps and the system constraints are satisfied at all discrete time instants, and (b) providing that (A, Q1/2) is observable, the state-input pair of the controlled system is asymptotically driven to the operating point and hence the output y(k) asymptotically tracks the given reference r.
Proof: If problem (22) is feasible with the initial state x(k) at time k, and an optimal solution is obtained with constraint (17) holding tightly, system constraints and the terminal constraint are satisfied by the predicted states and inputs at times k + i, i = 0, .., N - 1 and by the predicted terminal state x(k + N|k). If the input u(t) is applied to the system at times t ∈ [kT, kT + T) as mentioned in the scheme of Figure 4, the state x(k + 1) at time k + 1 is equal to the predicted state x(k + i|k) and the new optimization problem at time k + 1 is feasible with the input variables and , and with the predicted terminal state satisfying because of the invariance property (20) of the set . Hence, if problem (22) is feasible at time k = 0, part (a) of the proposition follows.
Next, to see part (b) of the proposition, note that since P satisfies the Lyapunov equation (19b), with the optimal state and input sequences predicted at time k, which remain feasible at time k + 1, we have
and hence the cost monotonicity condition
holds. This condition can be shown to ensure part (b) of the proposition using standard arguments (see, e.g., [1], [36]).
3.4 State Estimation and Control Implementation
The online steps in the MPC scheme of Figure 4 assume that the state x(k) can be measured exactly at every sampling instant and that the time varying control input u(t) can be implemented according to Equation (10). In practice, however, the state may not be measured fully (e.g., only the position of the magnetic object may be measured) or there may be errors in the measurement and the control input may be implemented in a more simplified form, using a constant or a linear approximation. The errors due to these factors can be incorporated in the system description (9) by adding a process disturbance term w(k) in the state equation and a measurement noise term η(k) in the output equation.
Under certain assumptions on the process and measurement disturbances, the state may be estimated using a Kalman filter. Even in the absence of reliable stochastic models of disturbances, the method can be used together with some learning or tuning mechanism that estimates the disturbance covariances (e.g., [37]). However, we consider a receding horizon state estimation using weighted batch least squares [38] to estimate the state. Consider a backward state propagation model based on (9), viz.,
where . Using this model, the stacked vector of states at the current and the past Ne time steps, i.e.,
can be written as
| (23) |
where and are defined just like and but with matrix A replaced by and
So, the stacked vector of outputs based on is given by
| (24) |
where . Defining the vector of measured outputs
the error vector is A weighted least squares estimate of x(k) that minimizes the weighted sum of errors , with a weight matrix W, is given by
where .
The presence of disturbances in the system dynamics model complicates the design of any controller, and some additional mechanism is usually adopted (e.g., [39]) to ensure robustness. In the MPC approach, a robust mechanism may be followed to guarantee the satisfaction of constraints in the presence of dis-turbances. However, assuming noises of small magnitudes, and relying on the inherent robustness of the MPC approach, we use the prediction model based on the nominal dynamics (9) as dis-cussed in Section 3.2.
For the implementation of the control input, we consider two alternative approximations to the time varying input u(t) for time t ∈ [kT, kT + T) – a linear approximation of (10) given by
| (25a) |
where and , and a constant approximation based on the time-averaged value of y(t) within the sampling period, given by
| (25b) |
where the values of the constant quantities Λ0, Λx and Λv are obtained from the definitions of q, q1 and q2. When the constant approximation (25b) is used, the two constraints in (15) can be replaced by a single matrix inequality constraint with the left-hand-side matrix having the off-diagonal block equal to
where and . This version of the constraint applies to the constant control input that is actually applied to the system during each sampling period.
Remark 2: In the analysis here, we have not incorporated the time delay in the implementation of the control action every time step due to the time spent in solving the MPC optimization problem. The effect of this time delay can be accounted for by either solv-ing the optimization problem for the predicted future state of the system or by incorporating the delay in the discrete-time system matrices as mentioned in [2].
4. Simulations
4.1 Basic Details
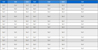
For the simulations in this section, we consider the values of the system parameters mentioned on the left side of Table 1.
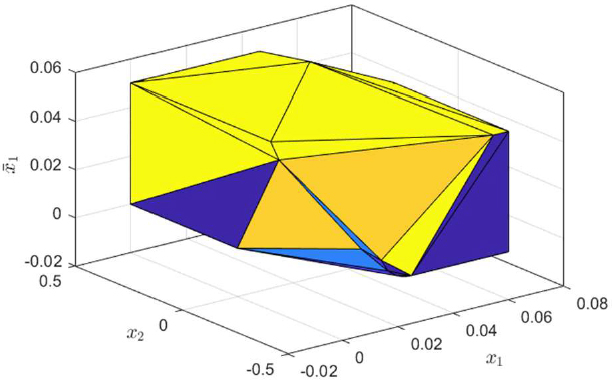
The limits considered in the constraints in (7) and the cost matrices used in defining the cost J(k) in Equation (16) are mentioned on the right side of Table 1. The terminal cost matrix P, the feedback gain K and the corresponding terminal invariant sets are determined as mentioned in Section 3.3. We consider only two segments and in and find the invariant sets and for system (20) with in and . The set obtained for and s is shown in Figure 5.
4.2 Assessment of Prediction Accuracy
We first assess the accuracy of the simplified multi-step predictions based on model (9) when linear and constant approximations (25a, b) of the optimal control inputs are applied to the plant. We consider the MPC optimization (22) for a target position with and compare the predicted values of the state components with their actual values obtained when the inputs predicted at time k = 0 are implemented using the nonlinear relation (10) and using its linear (25a) and constant (25b) approximations within each sampling period. The actual values obtained using u(t) as per (10) obviously coincide with the predicted values. The comparison results shown in Figure 6 for a sampling period T = 0.04s indicate that the actual values in the rest two cases are close to the predicted values through the full prediction horizon. With a smaller sampling period, the actual values remain further closer to the predicted values in both the cases.
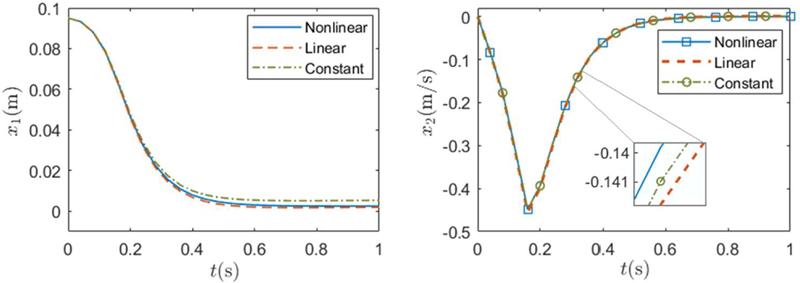
Position and velocity components of the state based on an exact nonlinear implementation of the control input in (10), a linear approximation of the input (25a) and a constant approximation of the input (25b) for T = 0.04s.
Figure 7 shows the magnitudes of the largest errors, wmax, i, i = 1, 2 in the update of the state components in (9) for various values of the sampling interval T when the control input is applied based on the approximations of (25a) and (25b). Note that, in this example, while the error in the update of x1 is smaller when the linear approximation is used, the error in the update of x2 is smaller when the constant approximation is used.
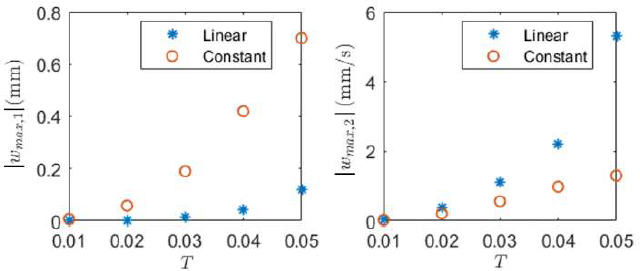
Largest modelling error component magnitudes in the state equation with linear and constant approximations of u(t).
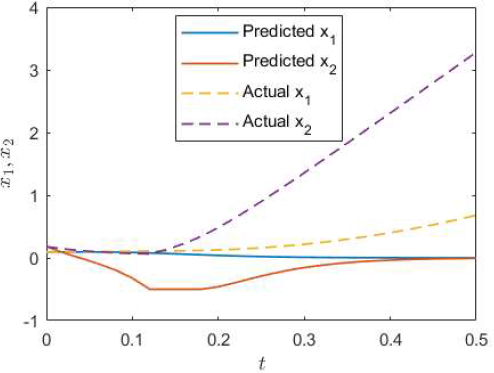
We also assess how the accuracy of the prediction approach explored in this paper compares with the accuracy of the predictions using the usual linearized model. We consider r = 0.0025 and linearize the nonlinear model about the operating point with . We discretize the linearized model for T = 0.04s and consider a finite horizon MPC problem with N = 20 for an initial state (0.095, 0). In Figure 8, predicted trajectories of the state components based on the optimal input sequence obtained at time k = 0 are compared with the actual trajectories obtained by applying this input sequence to the nonlinear system. It can be observed that the predictions are significantly off from actual values beyond a few steps. Note that while a receding horizon control based on these inaccurate predictions may still give a satisfactory control performance, there is no guarantee of stability and accurate set-point tracking with an MPC scheme based on these predictions.
4.3 Predictive Control Performance
Next, we evaluate the setpoint tracking performance with the overall MPC scheme outlined in Figure 4. Considering x(0) = (0, 0), we first choose r = 0.095 for up to 0.8s and then change the reference value to r = 0.0025. In the simulations, we consider, T = 0.04s and N = 10. Assuming that only the position is measured, we consider a zero-mean Gaussian sensor noise of standard deviation ση = 10-4 in the simulations, and to estimate the state, use a receding horizon state estimator with Ne = 5 and A diagonal weight matrix W is chosen with diagonal elements where em, i is an estimated upper bound of the magnitude of e(k - i|k) based partly on the observation in Figure 7 for the constant approximation (25b) and on an assumption that |η(k)| ≤ 2ση most of the times.
Figure 9 shows the actual and estimated trajectories of the state components under MPC when the control input u(t) is implemented using the constant approximation (25b). With a small sensor noise, the estimated state components are sufficiently close to the actual state components. Note that the position x1 reaches and remains close to the relevant set point before any change in the reference input. Also, the constraints on the state components are always satisfied.
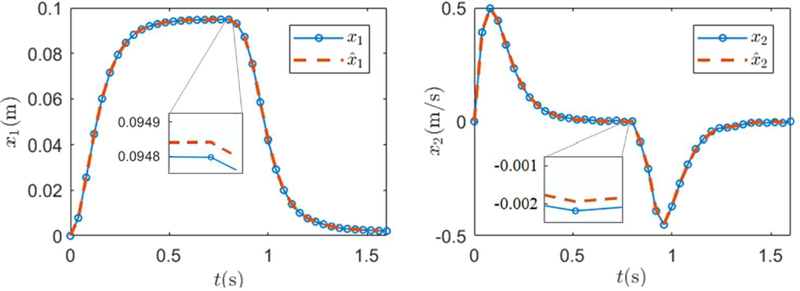
Actual and estimated position and velocity trajectories of the controlled system under the MPC scheme of Figure 4 for x(0) = (0, 0) and r = 0.095 for up to time 0.8s and r = 0.0025 from time 0.8s. Initial estimated state x^0=(0,0).
Figure 10 shows the actual control inputs applied to the sys-tem. The piecewise constant input trajectory of Figure 10 (left) pertains to the case when (25b) is used to approximate the time-varying control input whereas the piecewise affine input trajecto-ry of Figure 10 (right) is obtained when (25a) is used.
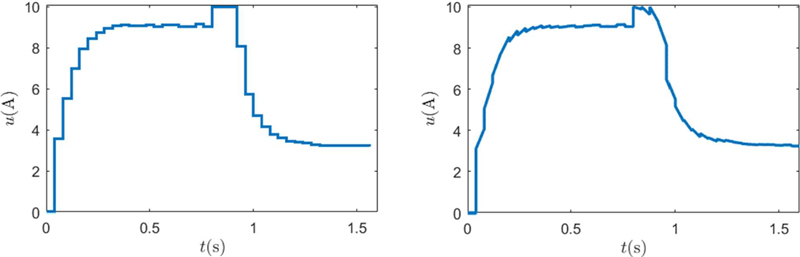
Control inputs applied to the system under the MPC scheme of Figure 4 when the constant approximation (25b) of (10) is used (left), and when the linear approximation (25a) of (10) is used (right).
Note that when (25b) is to be used, the two constraints in (15) are replaced by a single constraint as mentioned in Section 3.4. The input trajectories in both the cases satisfy the input con-straints.
4.4 Computational Requirements
The reformulated MPC optimization problem is convex and is solved as an SDP problem. The computational requirement for an SDP problem is typically higher than that for a QP problem which arises in the case of a linearized system with linear con-straints. Nevertheless, the convex reformulation provides a com-putationally efficient alternative to solve the original nonlinear MPC problem which is non-convex. Simulations in this section are carried out using the CSDP solver in MATLAB 2017b in a machine with 1.8GHz Intel i7 processor and 16 GB RAM. The mean computation times needed by the solver at each step in the simulations discussed in the previous subsection (with the input approximation of (25b)) are listed for three horizon lengths in Table 2.
These computation times are small for a small N but grow with increasing values of N. Since the sampling interval considered for the problem is T = 0.04s, if a large horizon length is needed for the problem, computational delay may need to be handled either with a more efficient solver for the specific structure of the problem or accounted for in the DT model of the system as mentioned earlier in Remark 2.
5. Conclusion
A real-time MPC scheme with a simplified prediction strategy was explored for the control of a nonlinear magnetic suspension system. The prediction strategy involves a linearizing transfor-mation of the input variable together with an accurate method of control input implementation, and a reformulation of the resulting constrained MPC optimization problem as a convex SDP prob-lem using semidefinite relaxation. Simulation results demonstrate the effectiveness of the proposed scheme for non-trivial sampling periods and prediction horizon.
Acknowledgments
This paper was supported by Education and Research promotion program of KOREATECH.
Author Contributions
All relevant contributions are by the Corresponding author.
References
-
D. Q. Mayne, “Model predictive control: Recent develop-ments and future promise,” Automatica, vol. 50, no. 12, pp. 2967-2986, 2014.
[https://doi.org/10.1016/j.automatica.2014.10.128]

- J. M. Maciejowski, Predictive Control with Constraints, England: Prentice Hall, 2002.
-
G. C. Goodwin, H. Kong, G. Mirzaeva, and M. M. Seron, “Robust model predictive control: reflections and opportuni-ties,” Journal of Control and Decision, vol. 1, no. 2, pp. 115-148, 2014.
[https://doi.org/10.1080/23307706.2014.913837]

-
T. A. N. Heirung, J. A. Paulson, J. O’Leary, and A. Mesbah, “Stochastic model predictive control – How does it work?,” Computers & Chemical Engineering, vol. 114, pp. 158-170, 2018.
[https://doi.org/10.1016/j.compchemeng.2017.10.026]

-
M. Zanon and S. Gros, “Safe reinforcement learning using Robust MPC,” IEEE Transactions on Automatic Control, vol. 66, no. 8, pp. 3638-3652, 2021.
[https://doi.org/10.1109/TAC.2020.3024161]

-
H. Guo, C. Shen, H. Zhang, H. Chen, and R. Jia, “Simulta-neous trajectory planning and tracking using an MPC meth-od for cyber-physical systems: A case study of obstacle avoidance for an intelligent vehicle,” IEEE Transactions on Industrial Informatics, vol. 14, no. 9, pp. 4273-4383, 2018.
[https://doi.org/10.1109/TII.2018.2815531]

-
S. Ruan, Y. Ma, and Q. Yan, “Adaptive cruise control for intelligent electric vehicles based on explicit model predic-tive control,” Lecture Notes on Electrical Engineering, vol. 804, pp. 860-869, 2022.
[https://doi.org/10.1007/978-981-16-6324-6_87]

-
L. Chisci, P. Falugi, and G. Zappa, “Gain-scheduling MPC of nonliear systems,” International Journal of Robust and Nonlinear Control, vol. 13 pp. 295-308, 2003.
[https://doi.org/10.1002/rnc.819]

-
V. M. Zavala and L. T. Biegler, “The advanced-step NMPC controller: optimality, stability and robustness,” Automatica, vol. 45, no. 1, pp. 86-93, 2009.
[https://doi.org/10.1016/j.automatica.2008.06.011]

-
P. Falugi, S. Olaru, and D. Dumur, “Robust multi-model predictive control using LMIs,” International Journal of Control, Automation and Systems, vol. 8, no. 2, pp. 169-175, 2010.
[https://doi.org/10.1007/s12555-010-0122-y]

-
A. Gautam and Y. C. Soh, “Stabilizing model predictive control using parameter-dependent dynamic policy for non-linear systems modeled with neural networks,” Journal of Process Control, vol. 36, pp. 11-21, 2015.
[https://doi.org/10.1016/j.jprocont.2015.09.003]

-
H. W. Lee, K. C. Kim, and J. Lee, “Review of Maglev train technologies,” IEEE Transactions on Magnetics, vol. 42, no. 7, pp. 1917-1925, 2006.
[https://doi.org/10.1109/TMAG.2006.875842]

-
J. Abbott, E. Diller, and A. Petruska, “Magnetic methods in robotics,” Annual Review of Control, Robotics, and Auton-omous Systems, vol. 3, pp. 57-90, 2020.
[https://doi.org/10.1146/annurev-control-081219-082713]

-
M. Maggiore and R. Becerril, “Modelling and control de-sign for a magnetic levitation system,” International Journal of Control, vol. 77, no. 10, pp. 964-977, 2004.
[https://doi.org/10.1080/002071704200024392]

-
C. Zhang and K. J. Tseng, “A novel flywheel energy stor-age system with partially self-bearing flywheel rotor,” IEEE Transactions on Energy Conversion, vol. 22, no. 2, pp. 477-487, 2007.
[https://doi.org/10.1109/TEC.2005.858088]

- A. Chiba, T. Fukao, O. Ichikawa, M. Oshima, M. Takemo-to, and D. G. Dorrell, Magnetic Bearings and Bearingless Drives, Elsevier, Amsterdam, The Netherlands, 2005.
- X. Song, A. L. Throckmorton, A. Untaroiu, S. Patel, P. E. Allaire, H. G. Wood, and D. B. Olsen, “Axial flow blood pumps,” ASAIO Journal, vol. 49, pp. 355–364, 2003.
-
X. Chu, “Two-terminal suspension adaptive control with synchronous compensation for Maglev wind turbine yaw system,” IEEE Transactions on Industrial Electronics, vol. 69, no. 10, pp. 10530-10540, 2022.
[https://doi.org/10.1109/TIE.2021.3135624]

-
S. Sivrioglu and K. Nonami, “Sliding mode control with time-varying hyperplane for AMB systems,” IEEE/ASME Transactions on Mechatronics, vol. 3, pp. 51-59, 1998.
[https://doi.org/10.1109/3516.662868]

-
K. Nonami, W. He, and H. Nishimura, “Robust control of magnetic levitation systems by means of H∞ control/μ-synthesis,” JSME International Journal Ser. C: Dynamics, Control, Robotics, Design and Manufacturing, vol. 37, pp. 513-520, 1994.
[https://doi.org/10.1299/jsmec1993.37.513]

-
Z. Zhang and X. Li, “Real-time adaptive control of a mag-netic levitation system with a large range of load disturb-ance,” Sensors, vol. 18, p. 1512, 2018.
[https://doi.org/10.3390/s18051512]

-
D. Rosinová and M. Hypiusová, “Comparison of nonlinear and linear controllers for magnetic levitation system,” Ap-plied Sciences, vol. 11, p. 7795, 2021.
[https://doi.org/10.3390/app11177795]

-
J. Wang and L. Yu, “Adaptive resonant-EIDO-Based opti-mized position precision control for magnetic levitation sys-tem,” IEEE Transactions on Industrial Electronics, vol. 70, no. 5, pp. 5013-5023, 2023.
[https://doi.org/10.1109/TIE.2022.3186348]

-
Z. Y. Sun, T. L. Xu, B. Cai, and C. C. Chen, “Robust adap-tive regulation of magnetic levitation systems with input quantization and external disturbances,” Journal of the Franklin Institute, vol. 360, no. 3, pp. 1672-1689, 2023.
[https://doi.org/10.1016/j.jfranklin.2022.12.022]

-
C. -H. Kim, “Robust control of magnetic levitation systems considering disturbance force by LSM propulsion systems,” IEEE Transactions on Magnetics, vol. 53, no. 11, pp. 1-5, 2017.
[https://doi.org/10.1109/TMAG.2017.2728810]

- R. C. Fama, R. V. Lopes, A. de P. Milhan, R. K. H. Galvão, and B. A. D. Lastra, “Predictive control of a magnetic levita-tion system with explicit treatment of operational con-straints,” ABCM Symposium Series in Mechatronics, vol. 2, pp. 1-8, 2006.
- M. S. Matos, R. K. H. Galvão, and T. Yoneyama, “Robust model predictive control for a magnetic levitation system employing linear matrix inequalities,” ABCM Symposium Series in Mechatronics, vol. 4, pp. 147-155, 2010.
-
A. Gautam, “Computationally efficient robust model predic-tive control of electromagnetic suspension systems,” Inter-national Journal of Electrical Engineering and Technology, vol. 11, no. 4, pp. 290-299, 2020.
[https://doi.org/10.34218/IJEET.11.4.2020.033]

-
T. Bächle, S. Hentzelt, and K. Graichen, “Nonlinear model predictive control of a magnetic levitation system,” Control Engineering Practice, vol. 21, no. 9, pp. 1250-1258, 2013.
[https://doi.org/10.1016/j.conengprac.2013.04.009]

-
A. Bonfitto, L. M. C. Molina, A. Tonoli, and N. Amati, “Offset-rree model predictive control for active magnetic bearing systems,” Actuators, vol. 7, no. 3, p. 46, 2018.
[https://doi.org/10.3390/act7030046]

-
W. Hu, Y. Zhou, Z. Zhang, and H. Fujita, “Model predic-tive control for hybrid levitation systems of maglev trains with state constraints,” IEEE Transactions on Vehicular Technology, vol. 70, no. 10, pp. 9972-9985, 2021.
[https://doi.org/10.1109/TVT.2021.3110133]

-
T. Peng, H. Peng, and R. Li, “Deep learning-based model predictive controller on a magnetic levitation ball system,” ISA Transactions, vol. 149, pp. 348-364, 2024.
[https://doi.org/10.1016/j.isatra.2024.04.019]

- H. K. Khalil, Nonlinear Systems, 3rd ed., Upper Saddle River, NJ: Prentice Hall, 2002.
-
S. Boyd and L. Vandenverghe, Convex Optimization, Cam-bridge University Press, 2004.
[https://doi.org/10.1017/CBO9780511804441]

-
F. Blanchini and S. Miani, Set-Theoretic Methods in Con-trol, Springer, 2008.
[https://doi.org/10.1007/978-0-8176-4606-6]

-
A. Gautam, Y.-C. Chu, and Y. C. Soh, “Optimized dynamic policy for receding horizon control of linear time-varying systems with bounded disturbances”, IEEE Transactions on Automatic Control, vol. 57, no. 4, pp. 973-988, 2012.
[https://doi.org/10.1109/TAC.2011.2170109]

-
C. Moon and Y. -A. Kwon, “Sensorless speed control of a permanent magnet synchronous motor using an unscented Kalman filter with compensated covariances,” Journal of Advanced Marine Engineering and Technology, vol. 44, no. 1, pp. 42-47, 2020.
[https://doi.org/10.5916/jamet.2020.44.1.42]

-
K. V. Ling and K. W. Lim, “Receding horizon recursive state estimation,” IEEE Transactions on Automatic Control, vol. 44, no. 9, pp. 1750-1753, 1999.
[https://doi.org/10.1109/9.788546]

-
S. -K. Hwang and B. -G. Jung, “A proposal for robust control performance on cascade control using IMC-based PID control and genetic algorithm,” Journal of Advanced Marine Engineering and Technology, vol. 47, no. 1, pp. 23-33, 2023.
[https://doi.org/10.5916/jamet.2023.47.1.23]