Computationally efficient trajectory tracking control of AUVs with nonlinear model predictive control using neural-based dynamics modeling

1. Introduction

Over the past several years, there has been an increasing aca-demic, technological and commercial interest in unmanned auton-omous systems operating in various environments – on ground and water, in air and space and under the sea [1]. An autonomous underwater vehicle (AUV) is a computer controlled robotic vehi-cle equipped with a propulsion system enabling its maneuvering in the three-dimensional (3D) space under the sea. Like other unmanned autonomous systems, AUVs have extensive scientific, military and commercial applications such as mapping and imag-ing of underwater landscapes, deep-sea exploration of marine life, inspection of underwater infrastructure, detection and clear-ance of pollutants and mines, undersea search and rescue and so on (see, e.g., [2]-[5]). Behind the successful design and operation of AUVs are various enabling technologies in the field of sens-ing, propulsion, communications, guidance, navigation and con-trol [6].

Target or trajectory tracking ability is very crucial for most AUV applications and this requires sophisticated navigation and control schemes since an AUV and the environment that it oper-ates in are characterized by high-dimensional nonlinear dynamics, often uncertain, constrained and underactuated, and usually un-predictable oceanic disturbances. Research on reliable control of AUVs is extensive and continuing [7]. A survey of early works on AUV control can be found in [8]. Traditional control design for AUVs includes various analytical design approaches employ-ing nonlinear feedback [9], gain-scheduled or parameterized line-ar feedback [10], input-output feedback linearization [11], and so on. To deal with control challenges owing to the highly nonlinear dynamics involving parameter uncertainties and disturbances, techniques such as sliding mode control [12] and adaptive control [13] have been tried and continue to be explored [14]-[16]. Al-ternative approaches that have been extensively explored include the more computation-oriented techniques such as those using fuzzy logic [17], and neural networks [18]-[19].

Control approaches explored in the works mentioned above do not directly deal with state and input constraints whose satisfac-tion is usually crucial in trajectory tracking applications. Model predictive control (MPC) is a promising computation-oriented control approach that handles constraints in a systematic way [20]. This approach is based on solving an open-loop control optimization problem online in real time and, with the advance-ments in computing hardware speed, the technology has become applicable for an increasing variety of linear and nonlinear control applications including trajectory planning and tracking applica-tions. Theoretical analysis of the method has also matured over the years [21]. MPC has been used for trajectory tracking control of marine vehicles in several earlier works [22]-[28]. Nonlinear MPC is used together with an unscented Kalman filter for posi-tioning of ships in [22]. In [23], the authors present a combina-tion of MPC and genetic algorithms to achieve dynamic trajectory tracking. Similarly, a Lyapunov-based MPC is explored for robust trajectory tracking of AUVs in [24]. An event-triggered nonlinear MPC is presented in [25] for trajectory tracking by an underactuated ship with reduced computational burden and a similar approach is used for AUVs in the presence of disturb-ances in [26]. In these schemes, the MPC optimization is carried out only when the vehicle’s deviation from the desired state is outside a chosen bound. In [27], a robust nonlinear MPC is de-signed to achieve robust trajectory tracking of underactuated AUVs in the presence of disturbance inputs.

While MPC offers a remarkable control performance, it is computationally demanding, which is particularly significant for nonlinear systems. So, a fast and reliable algorithm to solve the nonlinear MPC problem is always a necessity [28]. Since MPC is primarily envisaged in the discrete-time (DT) domain, an accu-rate DT model of the system is required, and is not readily ob-tained for a nonlinear system. Most MPC schemes use DT mod-els obtained using a simple Euler or Runge-Kutta (RK)-based discretization, which requires a very small sampling period to be considered. This limits the horizon length over which the MPC optimization can be carried out in real time, and it can be a draw-back in certain situations in trajectory tracking.

In this work, we present a trajectory tracking nonlinear MPC scheme that is based on an accurate modeling of the DT dynam-ics of the AUV and therefore allows an MPC optimization over a larger time horizon. In particular, we consider an AUV with four degrees of maneuverability and model its DT dynamics for a suitable sampling time with a feedforward neural network (NN). A network with a single hidden layer is chosen so that nested or sequential computations can be avoided during cost gradient computations. Such a model can be obtained for sampling inter-vals significantly larger than those that can be used with the ap-proximate methods. Following [29], we present a sequential quadratic programming (sQP) algorithm to solve the resulting NMPC problem for trajectory tracking. The sQP algorithm en-sures feasibility after each iteration and uses a simple trust region constraint to achieve convergence.

We verify the performance of the proposed tracking control scheme through extensive nonlinear simulations for an AUV mission in ideal and non-ideal scenarios. Non-ideal conditions include the presence of external disturbances and/or the failure of the control component along the transverse direction. Simulations show the effectiveness of the proposed approach.

Notations: I_n denotes an identity matrix of size n, 0_m×n denotes an m×n matrix of all zeros, and 1_n represents a n-dimensional vector of all ones. If any subscript is omitted, the dimension should be clear from the context. For a vector v, diag(v) represents a diagonal matrix with the elements of v along the diagonal, and with entities Δ₁, Δ₂, …, diag(Δ₁, Δ₂, …) represents a (block) diagonal matrix with Δ₁, Δ₂, … along the diagonal. For a vector $$ \mathbf{v},{‖\mathbf{v}‖}_{\mathit{Q}}^2$$ with a symmetric matrix Q represents the quadratic form $$ {\mathbf{v}}^{T}Q\mathbf{v}$$. For a DT signal x(k), x(k + i|k) denotes the future signal value x(k + i) predicted at time k.

2. System Description

2.1 Mathematical Model of AUV Motion

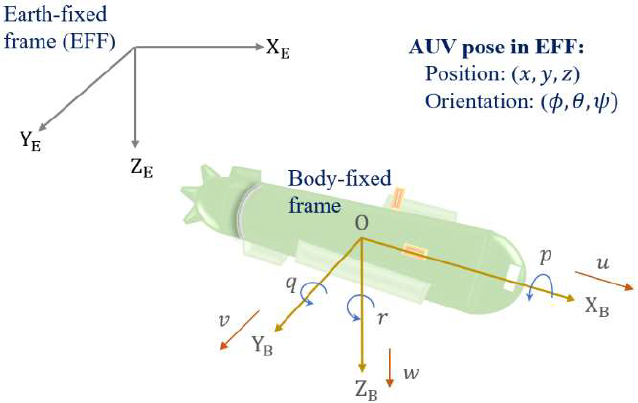
The motion of an AUV, like that of any marine vehicle, is conveniently described in 6 degrees of freedom (DOF) with its pose specified by its position p=(x, y, z) and its orientation θ=(ϕ, θ, ψ) (in terms of Euler angles) in an Earth-fixed coordinate frame X_E-Y_E-Z_E and its linear and angular velocities v=(u, v, w) and ω=(p, q, r) specified in a body-fixed reference frame X_B-Y_B-Z_B as illustrated in Figure 1. The origin O of the body-fixed frame is chosen at the vehicle’s center of gravity (CG) and its axes are chosen to coincide with the three principal axes of inertia – longitudinal, transverse and normal. So, the linear velocity components u, v and w correspond to surge, sway and heave speeds and the angular velocity components p, q and r correspond to roll, pitch and yaw speeds.

Figure 1:

Coordinate frames for describing AUV motion

The kinematic relationship between the pose vectors and the velocity vectors are given by

$$ \dot{\mathbf{p}}={\mathit{J}}_1\left(\mathbf{\theta }\right)\mathbf{v}, \dot{\mathbf{\theta }}={\mathit{J}}_2\left(\mathbf{\theta }\right)\mathbf{\omega }$$

where J₁ (θ) and J₂ (θ) are 3×3 transformation matrices with elements depending on ϕ, θ, ψ (see, e.g., [30] for the details).

In this paper, we consider underwater vehicles equipped with metacentric restoring forces preventing roll and pitch motions so that the roll and pitch angles ϕ and θ and the angular speeds p and q are negligible and close to zero. Under this assumption, the reduced-order kinematic relationship is described by

$\[ \dot{\mathbf{p}}={\mathit{J}}_1\left(\psi \right)\mathbf{v}=\left[\begin{array}{ccc}\mathrm{c}\mathrm{o}\mathrm{s} \psi & -\mathrm{s}\mathrm{i}\mathrm{n} \psi & 0\\ \mathrm{s}\mathrm{i}\mathrm{n} \psi & \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{c}\mathrm{o}\mathrm{s} \psi & 0\\ 0& 0& 1\end{array}\right]\mathbf{v}, \dot{\psi }=r \]$

(1)

Further, the dynamics of the vehicle are specified in terms of the combined velocity vector υ=(v, r) by the relationship

$\[ \mathit{M}\dot{\mathit{\upsilon }}+\mathit{C}\left(\mathbf{\upsilon }\right)\mathbf{\upsilon }+\mathit{D}\left(\mathbf{\upsilon }\right)\mathbf{\upsilon }+\mathbf{g}=\mathbf{\tau }+\mathbf{d} \]$

(2)

where M is the matrix of mass/inertia components (including the added mass/inertia), C(υ) is the matrix of Coriolis terms (including that of added mass/inertia), D(υ) is the hydrodynamic damping matrix, g is the vector of gravitational forces and moments, τ is the control input vector comprising forces and torques and d is the vector of disturbance forces/torques, mainly due to water currents. Assuming the AUV body to be symmetric about the x-y and x-z planes, and that it has a slightly positive buoyancy, we have,

$\[ \begin{array}{l}\mathit{M}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(m_X,m_Y,m_Z,I_Z\right),\\ \mathit{C}\left(\mathit{v}\right)=\left[\begin{array}{cccc}0& 0& 0& -m_{Y}v\\ 0& 0& 0& m_{X}u\\ 0& 0& 0& 0\\ m_{Y}v& -m_{X}u& 0& 0\end{array}\right]\\ \mathit{D}\left(\mathit{v}\right)=\begin{array}{l}-\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(X_u,Y_v,Z_w,N_r\right)\\ -\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(X_{u\left|u\right|}\left|u\right|,Y_{v\left|v\right|}\left|v\right|,Z_{w\left|w\right|}\left|w\right|,N_{r\left|r\right|}\left|r\right|\right)\end{array}\\ \mathbf{g}={\left[\begin{array}{c}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}B-W\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\end{array}\right]}^T\\ \mathit{\tau }={\left[\begin{array}{c}{\tau }_X\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\tau }_Y\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\tau }_Z\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\tau }_N\end{array}\right]}^T\end{array} \]$

where W and B are the weight and the buoyancy of the vehicle, and, m_X, m_Y, m_Z, I_Z are mass/inertia terms (including added mass/inertia), X_u, Y_v, Z_w, N_r and X_u|u|, Y_v|v|, Z_w|w|, N_r|r| are hydrodynamic damping terms, τ_X, τ_Y, τ_Z, τ_N are the control forces/torque generated by the thrusters and d_X, d_Y, d_Z, d_N are disturbance forces/torque effective along/about the surge, sway, heave and yaw directions.

Thus, combining Equations (1) and (2), we can write the mathematical description of the AUV motion in the 3D space in the form of the following nonlinear state-space model

$\[ \dot{\mathbf{x}}=\mathit{f}\left(\mathbf{x},\mathbf{u},\mathbf{d}\right), \mathbf{y}=C \mathbf{x} \]$

(3)

where $$ \mathbf{x}={\left[x y z \psi u v w r\right]}^T\in {\mathbb{R}}^8$$ is the state vector, $$ \mathbf{u}=\mathbf{\tau }\in {\mathbb{R}}^4$$ is the control input vector, $$ \mathbf{d}\in {\mathbb{R}}^4$$ is the disturbance input vector, and

$\[ \mathit{f}\left(\mathbf{x},\mathbf{u},\mathbf{d}\right)=\left[\begin{array}{c}u\cos \psi -v\sin \psi \\ u\sin \psi +v\cos \psi \\ w\\ r\\ \frac{1}{m_X}(m_{Y}vr+{(X}_u+X_{u\left|u\right|}\left|u\right|)u+{\tau }_X+d_X) \\ \frac{1}{m_Y}(-m_{X}ur+{(Y}_v+Y_{v\left|v\right|}\left|v\right|)v+{\tau }_Y+d_Y)\\ \frac{1}{m_Z}(W-B+{(Z}_w+Z_{w\left|w\right|}\left|w\right|)w+{\tau }_Z+d_Z)\\ \frac{1}{I_Z}\left(\right(m_X-m_Y)uv+{(N}_r+N_{r\left|r\right|}\left|r\right|)r+{\tau }_N+d_N)\end{array}\right] \]$

Further, the output vector $$ \mathbf{y}=C_{\mathbf{X}}={\left[x y z \psi \right]}^T\in {\mathbb{R}}^4$$ so that $$ =\left[I_4 0_{4\times 4}\right]$$.

Remark 1: The motion of an AVU described by (3) has 4 DOF and is supported by control inputs along the 4 directions. The AUV can still be maneuvered if the sway input component τ_Y is unavailable or the corresponding actuator is faulty. A vehicle in such a situation is considered to be underactuated. Several works on AUV trajectory tracking control have focused on underactuated AUVs (e.g., [27])

3. AUV Trajectory Tracking with NMPC using Neural-Modeled System Dynamics

4. Numerical Simulations

4.1 AUV Details

Extensive simulations are carried out to assess the performance of the proposed approach. Parameters specifying the dynamics of the AUV and the constraints applicable on speeds and thruster actions are mentioned in Table 1.

Table 1:

AUV dynamics parameters and constraints

4.2 AUV DT Dynamics Modeling with NNs

We obtain two ff-NNs – NN-1 and NN-2 to represent nonlinear DT dynamics for two different sampling periods – T₁ = 1s and T₂ = 0.25s. Both are trained with about 10000 samples of input-output data. Input data samples are selected randomly from the set $$ 1.1(\left[-\pi , \pi \right]\times G\mathbb{X}\times \mathbb{U}$$) where the set [-π, π] is the range chosen for the yaw angle ψ. The factor 1.1 is used to provide some margin at the constraint boundaries. Outputs corresponding to input samples are obtained using the ode45 solver in MATLAB. Networks NN-1 and NN-2 are designed with η₁ = 48 and η₂ = 40 hidden layer neurons which use the tanh() activation function. After sufficient training, their mean squared error (MSE) performances are found to be of the order 10^-5 and 10^-6 respectively.

Table 2 gives a comparison, in terms of accuracy and computational efficiency, of model NN-2 with the popular RK-4 method (which is used, e.g., in [22], [26]). Here, the model accuracy is indicated by the MSE over all training and test samples, and, the computational efficiency is expressed in terms of the ratio of the average model function evaluation time over the average time taken by the accurate ode45 method in the same machine. While NN-2 is expectedly more accurate for this step size, what is significant is its comparative computational advantage which should remain significant (for both function evaluation and gradient evaluation) even for small step sizes for which the accuracy advantage may not be significant. Note that the RK-4 method is not stable with the time step size h = 1.

Table 2:

Comparison of approximations with NN-2 and RK-4

4.3 AUV Mission Simulation with NMPC

For tracking control performance evaluation, we consider an AUV mission comprising predefined time-varying trajectory tracking and free set-point tracking segments. In particular, the following phases are considered in the mission:

• 1) Descending phase: Trajectory tracking phase 1 (100s)
  $$ x_d\left(t\right)=2+0.2t, y_d\left(t\right)=1+0.05t, $$
  $$ z_d\left(t\right)=22-20e^{-\frac{{\left(x_d\left(t\right)-2\right)}^2+{\left(y_d\left(t\right)-1\right)}^2}{25}}$$
• 2) Free set-point tracking phase (No fixed target time)
  $$ \left(x_d,y_d,z_d\right)=\left(\mathrm{60,10,30}\right) $$
• 3) Object inspection phase (Trajectory tracking phase 2 (800s))
  $$ x_d\left(t\right)=71-10\cos \left(0.05(t-t_2)\right) + 0.01(t-t_2)$$
  $$ y_d\left(t\right)=10+8\sin \left(0.05\right(t-t_2\left)\right), $$
  $$ z_d\left(t\right) = 30-0.025(t-t_2)$$

where t₂ is the time when Phase 2 is completed.

We assume that the AUV is initially at rest at (0, 0, 0).

4.3.1 Performance in Disturbance-Free Scenario

We first consider the case without disturbances in the simulation model. In the MPC cost function, we use the cost matrix Q = diag(I₄, 0.1I₄ ) in all phases, and since the desired inputs are not specified, we mildly penalize the actual inputs with R = 10^-5I₄ in Phases 1 and 3 and R = 10^-3I₄ in Phase 2. We also look for a horizon length N that is sufficient to ensure that the predicted terminal state is close to the desired pose throughout the mission. It is found that with model NN-1 (T₁ = 1s), a horizon length of N = 10 is generally sufficient when the initial state is not very far from the corresponding reference point. In Phase 2, the target point is initially not close but to avoid using a large horizon length, we consider a virtual reference converging to the target point (60, 10, 30) and update the virtual reference in real time.

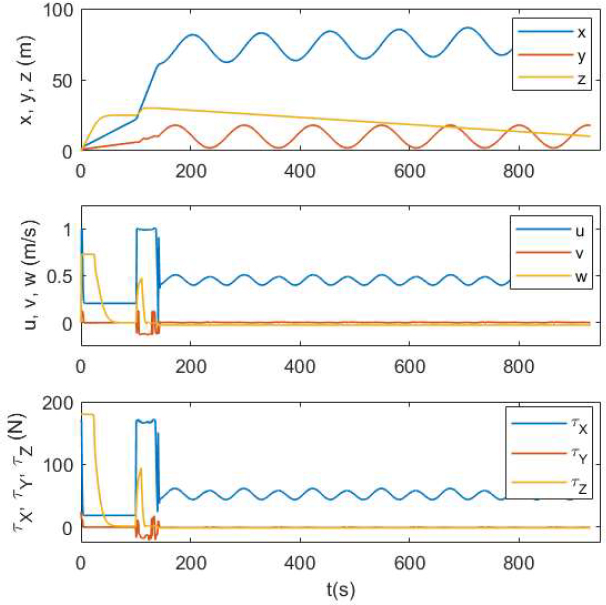
Figure 2 shows the reference and actual AUV position trajec-tories that we achieve with the MPC scheme using model NN-1 in the disturbance-free scenario. It can be seen that the MPC is able to drive the AUV closely along the desired trajectory.

Figure 2:

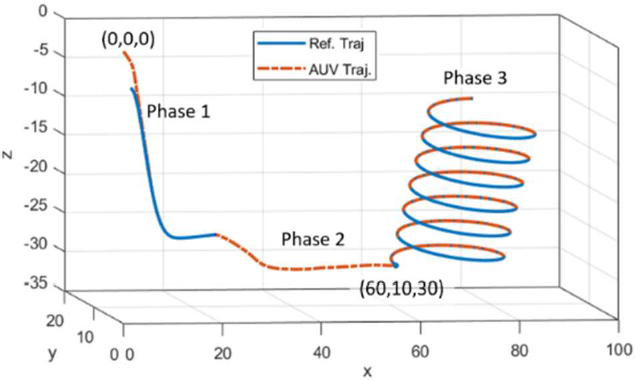
AUV trajectory obtained with the MPC scheme in disturbance-free scenario, alongside the reference trajectory

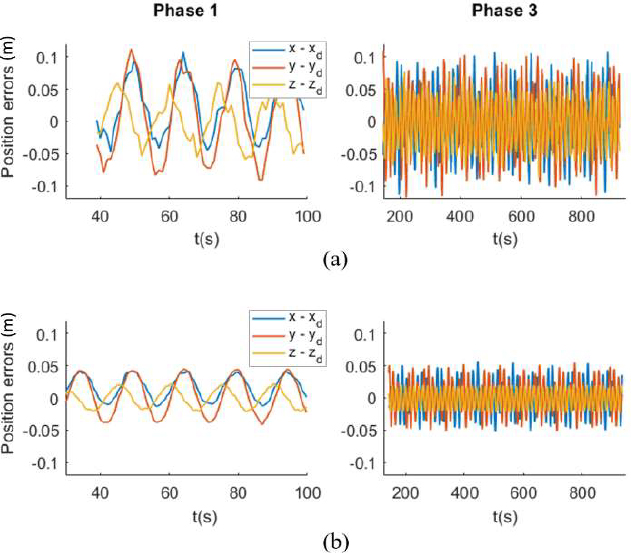
Figure 3 shows the position and velocity components of the AUV state and the thruster forces in x-, y-, z- directions. It can be seen that the z-direction thruster reaches the limit during Phase 1 when the decent is steep. Similarly, the surge and sway speed limits are reached during Phase 2. Figure 4(a) shows the position tracking errors during Phase 1 and 3, and it can be seen from the figure that the tracking error is within ±0.025m in each dimension. Note that the tracking error is not relevant in Phase 2.

Figure 3:

Position, velocity and thruster force components during AUV mission in disturbance-free scenario

Figure 4:

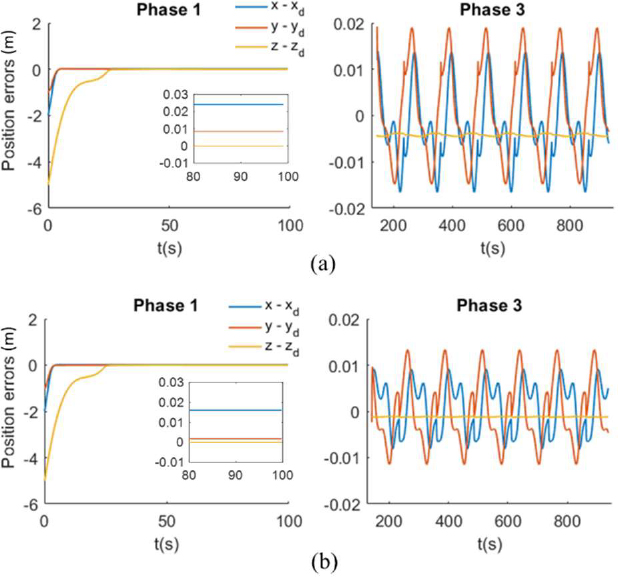
Position tracking errors in Phases 1 and 3 in disturbance-free scenario: (a) with model NN-1, (b) with model NN-2

In order to assess the impact of the accuracy of the dynamics model, we also simulate the performance of the MPC scheme with model NN-2. Since NN-2 uses a sampling time of 0.25s, a horizon length of 10s would require N = 40. However, since the input can be updated quickly, we consider N = 10 as earlier. The tracking response is similar to the one obtained with NN-1. However, as we can see in Figure 4(b), which presents the position tracking errors during Phase 1 and Phase 3, the tracking errors are smaller with NN-2 than with NN-1.

This can be expected since model NN-2 is at least one order of magnitude more accurate (in terms of MSE values) than NN-1 and it also updates the control actions 4 times more frequently.

4.3.2 Performance in the Presence of Disturbances

We next consider a scenario with disturbance inputs. Disturb-ances are mainly due to water currents inside the sea and are slowing varying in time but there can be other sources too. We consider a disturbance vector of the following form:

$\[ \mathbf{d}=\left[\begin{array}{c}8\sin \left(0.1t\right)+2v_1\\ 8\cos (0.1t-0.3)+{2v}_2\\ 8\cos (0.1t+0.8)+2v_3\\ 2\sin \left(0.1t+0.5\right)+0.05v_4\end{array}\right] \]$

where $$ v_1,v_2,v_3,v_4$$ are zero-mean Gaussian random variables with unit variance.

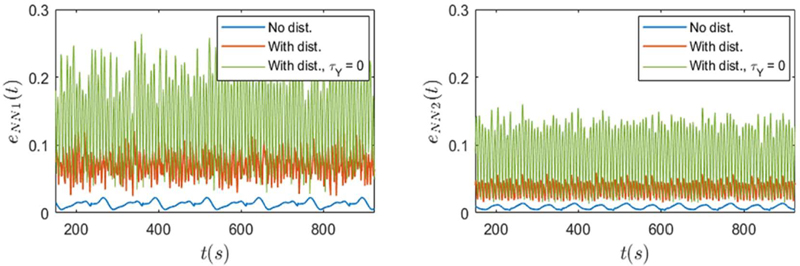
Figure 5 shows the tracking errors in Phases 1 and 3 in the presence of disturbance inputs. The errors in Part (a) are for the scheme with NN1 and those in Part (b) are for that with NN-2. Note that the transient phase is not shown. Evidently, the error magnitudes in the presence of disturbances are larger by a factor of about 5 (compare with Figure 4). Also, the error magnitudes are lower by about 50% with NN-2 than with NN-1 for reasons mentioned above. Nevertheless, the MPC scheme is able to limit the tracking errors within about 10cm in each direction when NN-1 is used and within about 5cm when NN-2 is used.

Figure 5:

Position tracking errors in Phases 1 and 3 in the presence of disturbances: (a) with model NN-1, (b) with model NN-2

4.3.3 Performance in the Absence of Sway Control

In this part, we explore the performance of the MPC scheme in a scenario with a faulty sway (transverse direction) actuator. Even without a fault, the sway control considered in our scheme is limited because of the limitation in sway speed and sway-direction thrust. When sway control is completely absent, the AUV is considered to be underactuated and its maneuvering ability may be restricted in some situations. We consider this situation in the presence of disturbances as mentioned in Section 4.3.2. Figure 6 shows the state and control components evolving under the MPC scheme (using NN-1) in this scenario. It can be observed that while the control inputs (except τ_Y, which is zero) and the velocities react and fluctuate to correct the effect of the disturbances that affect the system, position components vary rather smoothly with time.

Figure 6:

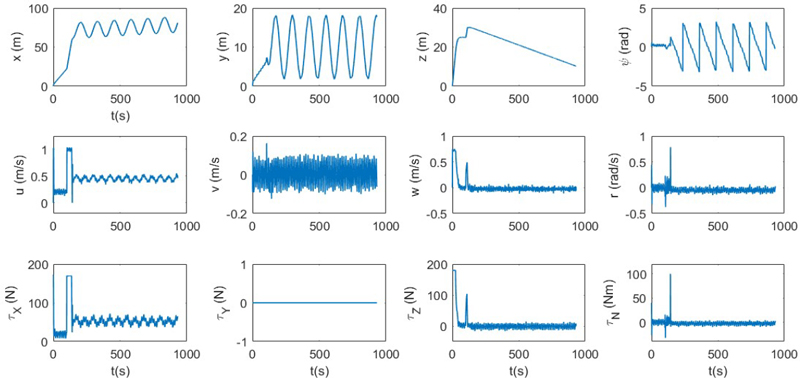
The evolution of state and control components during the mission without sway control in the presence of disturbances

The plots in Figure 7 show 3D position errors $$ (e=\sqrt{{\left(x-x_d\right)}^2+{\left(y-y_d\right)}^2+{\left(z-z_d\right)}^2} ) $$ during Phase 3 in the three different scenarios considered (in Sections 4.3.1~4.3.3).

Figure 7:

3D position tracking errors in various scenarios with dynamics models NN-1 and NN2

The errors in the first figure are obtained with model NN-1 and those in the second figure are obtained with model NN-2. Clearly, the presence of disturbances increases the tracking error and the actuator fault further increases it. And, because of higher accuracy and smaller sampling time, with model NN-2, errors are smaller by a factor of about 2.

4.3.4 Computational Requirements

Solving the nonlinear MPC problem is computationally demanding. Algorithm 2 requires a repeated solution of a QP problem at every time step. It is found that, except at the first step of every phase, the algorithm converges in up to 4 or 5 steps. The initial step requires the search for an initial feasible solution which may take 5 to 10 or more steps depending on the horizon length. We use the QP solver qpOASES [36] in MATLAB in a Windows machine with Intel i7 1.8 GHz processor and 24 GB RAM for the computations. It is found that the computations (QP solving and other preparatory computations) to be made after the measurement of the state at each step to obtain the optimal solution take, on the average, about 19ms when NN-1 is used and about 15ms when NN-2 is used for a horizon length of N = 10. In the absence of sway control, since we have a fewer number of optimization variables, the corresponding average computation times are slightly smaller – 15ms and 12ms respectively. Clearly, these computation times are small fractions of the respective sampling times and therefore they do not adversely affect the implementability of the control scheme.

5. Conclusion

The problem of 3D trajectory tracking of AUVs under 4 or 3 degrees of maneuverability was addressed with an effective and efficient nonlinear MPC scheme that uses a suitable modeling of the DT dynamics of the system using a ff-NN. An accurate NN-based DT dynamics model simplifies the online state propagation and cost gradient computations when solving the nonlinear MPC optimization problem with a sequence of QPs. Realistic numeri-cal simulations have shown the effectiveness of the approach in various situations including the presence of random and non-random disturbances and/or the lack of maneuverability along the sway direction.

Acknowledgments

This paper was supported by Education and Research promotion program of KOREATECH.

References

• T. Fossen, K. Y. Pettersen, and H. Nijmeijer, Sensing and Control for Autonomous Vehicles: Applications to Land, Water and Air Vehicles, Lecture Notes in Control and In-formation Sciences, vol. 474, 2017. [https://doi.org/10.1007/978-3-319-55372-6]
• H. Singh, C. Roman, O. Pizarro, R. Eustice, and A. Can, “Towards high-resolution imaging from underwater vehi-cles,” The International Journal of Robotics Research, vol. 26, no. 1, pp. 55-74, 2007. [https://doi.org/10.1177/0278364907074473]
• D. Sward, J. Monk, and N. Barrett, “A systematic review of remotely operated vehicle surveys for visually assessing fish assemblages,” Frontiers in Marine Science, vol. 6, 2019. [https://doi.org/10.3389/fmars.2019.00134]
• L. Wang, D. Zhu, W. Pang, and Y. Zhang, “A survey of underwater search for multi-target using multi-AUV: Task allocation, path planning, and formation control,” Ocean Engineering, vol. 278, 114393, 2023. [https://doi.org/10.1016/j.oceaneng.2023.114393]
• R. B. Wynn, et al., “Autonomous Underwater Vehicles (AUVs): Their past, present and future contributions to the advancement of marine geoscience,” Marine Geology, vol. 352, pp. 451-468, 2014. [https://doi.org/10.1016/j.margeo.2014.03.012]
• A. Wibisono, M. J. Piran, H. -K. Song, and B. M. Lee, “A survey on unmanned underwater vehicles: Challenges, ena-bling technologies, and future research directions,” Sensors, vol. 23, no. 17, p. 7321, 2023. [https://doi.org/10.3390/s23177321]
• A. Bashir, S. Khan, N. Iqbal, S. Bashmal, S. Ullah, Fayyaz, and M. Usman, “A review of the various control algorithms for trajectory control of unmanned underwater vehi-cles,” Sustainability, vol. 15, no. 20, p. 14691, 2023. [https://doi.org/10.3390/su152014691]
• J. Yuh, “Design and control of autonomous underwater robots: A survey,” Autonomous Robots, vol. 8, pp. 7-24, 2000. [https://doi.org/10.1023/A:1008984701078]
• K. Y. Pettersen and O. Egeland, “Time-varying exponential stabilization of the position and attitude of an underactuated autonomous underwater vehicle,” IEEE Transactions on Automatic Control, vol. 44, no. 1, pp. 112-115, 1999. [https://doi.org/10.1109/9.739086]
• C. Silvestre and A. Pascoal, “Control of the INFANTE AUV using gain scheduled static output feedback,” Control Engineering Practice, vol. 12, no. 12, pp. 1501-1509, 2004. [https://doi.org/10.1016/j.conengprac.2004.02.012]
• C. Paliotta, E. Lefeber, K. Y. Pettersen, J. Pinto, M. Costa and J. T. de F. B. de Sousa, “Trajectory tracking and path following for underactuated marine vehicles,” IEEE Trans-actions on Control Systems Technology, vol. 27, no. 4, pp. 1423-1437, 2019. [https://doi.org/10.1109/TCST.2018.2834518]
• M. Mat-Noh, R. Mohd-Mokhtar, M. R. Arshad, Z. M. Zain, and Q. Khan, “Review of sliding mode control application in autonomous underwater vehicles,” Indian Journal of Geo Marine Sciences, vol. 48, no. 7, pp. 973-984, 2019.
• J. Nie, J. Yuh, E. Kardash, and T. I. Fossen, “On-board sensor-based adaptive control of small UUVs in very shal-low water,” International Journal of Adaptive Control and Signal Processing, vol. 14, no. 4, pp. 441-452, 2000. [https://doi.org/10.1002/1099-1115(200006)14:4<441::AID-ACS565>3.0.CO;2-M]
• J. Guerrero, J. Torres, V. Creuze, and A. Chemori, “Trajec-tory tracking for autonomous underwater vehicle: An adap-tive approach,” Ocean Engineering, vol. 172, pp. 511-522, 2019. [https://doi.org/10.1016/j.oceaneng.2018.12.027]
• Z. Yan, M. Wang, and J. Xu, “Robust adaptive sliding mode control of underactuated autonomous underwater ve-hicles with uncertain dynamics,” Ocean Engineering, vol. 173, pp. 802-809, 2019. [https://doi.org/10.1016/j.oceaneng.2019.01.008]
• L. Qiao and W. Zhang, “Trajectory tracking control of AUVs via adaptive fast nonsingular integral terminal sliding mode control,” IEEE Transactions on Industrial Informatics, vol. 16, no. 2, pp. 1248-1258, 2020. [https://doi.org/10.1109/TII.2019.2949007]
• B. Sun, D. Zhu, and S. Yang, “An optimized fuzzy control algorithm for three-dimensional AUV path planning,” Inter-national Journal of Fuzzy Systems, vol. 20, no. 5, pp. 1-14, 2017. [https://doi.org/10.1007/s40815-017-0403-1]
• B. S. Park, “Neural network-based tracking control of un-deractuated autonomous underwater vehicles with model uncertainties,” Journal of Dynamic Systems, Measurement, and Control, vol. 137, no. 2, p. 021004, 2015. [https://doi.org/10.1115/1.4027919]
• J. Li, J. Du, and C. L. P. Chen, “Command-filtered robust adaptive NN control with the prescribed performance for the 3-D trajectory tracking of underactuated AUVs,” IEEE Transactions on Neural Networks and Learning Systems, vol. 33, no. 11, pp. 6545-6557, 2022. [https://doi.org/10.1109/TNNLS.2021.3082407]
• J. M. Maciejowski, Predictive Control with Constraints, Prentice Hall, Harlow, England, 2002.
• J. Köhler, M. A. Müller, and F. Allgöwer, “Nonlinear refer-ence tracking: An economic model predictive control per-spective,” IEEE Transactions on Automatic Control, vol. 64, no. 1, pp. 254-269, 2019. [https://doi.org/10.1109/TAC.2018.2800789]
• A. Jayasiri, A. Nandan, S. Imtiaz, D. Spencer, S. Islam, and S. Ahmed, “Dynamic positioning of vessels using a UKF-based observer and an NMPC-based controller,” IEEE Transactions on Automation Science and Engineering, vol. 14, no. 4, pp. 1778-1785, 2017. [https://doi.org/10.1109/TASE.2017.2698923]
• W. Gan, D. Zhu, and D. Ji, “QPSO-model predictive con-trol-based approach to dynamic trajectory tracking control for unmanned underwater vehicles,” Ocean Engineering, vol. 158, pp. 208-220, 2018. [https://doi.org/10.1016/j.oceaneng.2018.03.078]
• C. Shen, Y. Shi, and B. Buckham, “Trajectory tracking control of an autonomous underwater vehicle using Lya-punov-based model predictive control,” IEEE Transactions on Industrial Electronics, vol. 65, no. 7, pp. 5796-5805, 2018. [https://doi.org/10.1109/TIE.2017.2779442]
• C. Liu, Q. Hu, X. Wang, and J. Yin, “Event-triggered-based nonlinear model predictive control for trajectory tracking of underactuated ship with multi-obstacle avoidance,” Ocean Engineering, vol. 253, 111278, 2022. [https://doi.org/10.1016/j.oceaneng.2022.111278]
• W. Zhang, Q. Wang, W. Wu, X. Du, Y. Zhang, and P. Han, “Event-trigger NMPC for 3-D trajectory tracking of UUV with external disturbances,” Ocean Engineering, vol. 283, 115050, 2023. [https://doi.org/10.1016/j.oceaneng.2023.115050]
• S. Heshmati-Alamdari, A. Nikou, and D. V. Dimarogonas, “Robust trajectory tracking control for underactuated auton-omous underwater vehicles in uncertain environments,” IEEE Transactions on Automation Science and Engineering, vol. 18, no. 3, pp. 1288-1301, 2021. [https://doi.org/10.1109/TASE.2020.3001183]
• C. Shen, B. Buckham, and Y. Shi, “Modified C/GMRES algorithm for fast nonlinear model predictive tracking con-trol of AUVs,” IEEE Transactions on Control Systems Technology, vol. 25, no. 5, pp. 1896-1904, 2017. [https://doi.org/10.1109/TCST.2016.2628803]
• A. Gautam and Y. C. Soh, “Stabilizing model predictive control using parameter-dependent dynamic policy for non-linear systems modeled with neural networks,” Journal of Process Control, vol. 36, pp. 11-21, 2015. [https://doi.org/10.1016/j.jprocont.2015.09.003]
• T. I. Fossen, Guidance and Control of Ocean Vehicles, John Willey & Sons, 1994.
• P. A. Miller, J. A. Farrell, Y. Zhao, and V. Djapic, “Auton-omous underwater vehicle navigation,” IEEE Journal of Oceanic Engineering, vol. 35, no. 3, pp. 663-678, 2010. [https://doi.org/10.1109/JOE.2010.2052691]
• Y. -S. Han, M. -J. Kim, H. -I. Seo, and D. -H. Seo, “Direct orientation estimation through inertial odometry based on a deep transformer model,” Journal of Advanced Marine En-gineering and Technology, vol. 48, no. 2, pp. 96-106, 2024. [https://doi.org/10.5916/jamet.2024.48.2.96]
• D. Q. Mayne, E. C. Kerrigan, E. V. Wyk, and P. Falugi, “Tube-based robust nonlinear model predictive control,” In-ternational Journal of Robust and Nonlinear Control, vol. 21, no. 11, pp. 1341-1353, 2011. [https://doi.org/10.1002/rnc.1758]
• A. Gautam, Y. -C. Chu, and Y. C. Soh, “Optimized dynam-ic policy for receding horizon control of linear time-varying systems with bounded disturbances,” IEEE Transactions on Automatic Control, vol. 57, no. 4, pp. 973-988, 2012. [https://doi.org/10.1109/TAC.2011.2170109]
• S. J. Wright and M. J. Tenny, “A feasible trust-region se-quential quadratic programming algorithm,” SIAM Journal of Optimization, vol. 14, no. 4, pp. 1074-1105, 2004. [https://doi.org/10.1137/S1052623402413227]
• H. J. Ferreau, C. Kirches, A. Potschka, H. G. Bock, and M. Diehl, “A parametric active-set algorithm for quadratic pro-gramming,” Mathematical Programming Computation, vol. 6, no. 4, pp. 327-363, 2014. [https://doi.org/10.1007/s12532-014-0071-1]