Optimization study of BOG re-liquefaction process for ammonia fueled ship
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This study presents a study on the optimization of the boil-off gas (BOG) re-liquefaction system for ammonia fueled ship using a program developed with HYSYS and Python. The main objective of the research is to improve the energy efficiency of the process system. The process system was modeled using HYSYS, and an optimization program was implemented through integration with Python. Therefore, an optimization tool was developed using genetic algorithms and the penalty function method. Variables for optimization included the discharge pressures of each compressor stage and the side stream flow rate. The optimization aimed to maximize the coefficient of performance (COP) as the objective function. The results showed that the initial COP of 1.714 improved to 1.923, representing an approximate 12% enhancement. This study provides significant findings that contribute to the efficient operation of re-liquefaction systems for ammonia fueled ship.
Keywords:
Ammonia fueled ship, Boil-off gas, Re-liquefaction system, Optimization study, Genetic algorithm1. Introduction
Greenhouse gases have been identified as the primary cause of global climate change. The United Nations has committed to limiting the increase in global average temperatures to less than 2℃ above pre-industrial levels, with the goal of mitigating the severe impacts of global warming [1]. Based on above, the IMO has set a decarbonization goal to decrease greenhouse gas emissions in shipping by at least 50% by 2050 [2]. However, in 2023, MEPC has aspired to reduce carbon intensity by at least 40% by 2030 compared to 2008, and to be carbon-free by 2050 [3]. This objective has prompted research worldwide on using renewable energy and zero-carbon alternative fuels [4].
Reducing carbon emissions from ships can be achieved through various methods, including the use of alternative fuels either alone or in combination with conventional fuels, as part of the IMO's carbon reduction strategies [5]. Liquefied natural gas (LNG) and methanol are prominent alternatives to heavy fuel oil (HFO) and marine diesel oil (MDO) due to their lower carbon emissions [6]. Notably, hydrogen and ammonia, which contain no carbon atoms, are seen as key fuels for achieving the IMO 2050 targets of zero carbon emissions [7].
Consequently, the consumption of HFO and MGO in Europe is anticipated to decline significantly by 2050. While the cost and greenhouse gas emissions are major factors influencing the selection of alternative fuels, it is evident that technical maturity, safety regulations, and user experience still pose challenges. Nevertheless, the maritime sector is expected to rapidly transition to alternative fuels, with ammonia likely playing a major role [8][9].
Ammonia does not emit carbon dioxide when burned, making it an environmentally friendly fuel option. Additionally, nitrogen, which is one of the primary components of ammonia, is abundantly available in the atmosphere and is relatively easy to obtain. Liquefied ammonia is denser than its gaseous form, and it has a boiling point of below -33.4℃ at atmospheric pressure. Therefore, fuel tanks or cargo tanks designed to store liquefied ammonia are specifically engineered with insulation to prevent evaporation caused by heat. The generation of BOG is influenced by the tank's design, which includes factors such as the thickness of the insulation and the design pressure of the tank [10].
To use ammonia as a fuel for ships, relevant international regulations must be complied with. In major classification societies, ammonia gas generated during operation must be treated and discharged at 25 ppm or less when released into the atmosphere, and regulations related to the pressure holding time of fuel tanks must be considered. The ammonia to be used as fuel for ships is green ammonia, which is very expensive. Therefore, unless a pressurized tank is used, it is judged to be more economical to use it as fuel or re-liquefy it and store it in a tank rather than combust it [11][12].
In this paper, a Python-based optimization program for re-liquefying and treating ammonia evaporation gas, which has not been covered in previous studies, was developed. Additionally, a study on process system engineering and optimization based on actual ship specifications was conducted.
2. Research Method
2.1 System Description
To configure the BOG re-liquefaction system for an ammonia fueled ship, the size of the fuel tank was first determined. Even for the same ship type, the size of the fuel tank may vary depending on the ship owner's requirements and the ship's route. In this paper, the capacity of the fuel tank was calculated based on the size needed for a 60-day voyage at the normal power output (NCR) of the main engine applied to a 320,000 dwt VLCC, and the tank size was set to 15,000 m³ considering the loading limit [13]-[15]. The process design for the BOG treatment system can be carried out by knowing the amount of BOG that needs to be treated. Calculations were performed by referring to the surface area and insulation thickness information of the Type-A tank applied to the actual project [16]. The IMO type-A tank is primarily used in VLGC and VLAC for actual project. The calculation was performed based on spray-type insulation, which has recently been widely used as insulation for Type-A tanks in ships, and the thickness of the insulation was set at 125 mm, the same as the thickness of insulation for LPG and ammonia carriers [17][18]. According to research by Marina Gravit et al., the thermal conductivity of PUF (polyurethane foam) and PIR (polyisocyanurate) insulation materials, which are commonly used in Type-A independent tanks of ships, varies depending on the supplier. In this study, the boil-off rate (BOR) was calculated using the thermal conductivity of BASF’s PUF material, as shown in the equation (1) below [17].
| (1) |
Where Q represents total heat flow rate, ρ represents density of fluid, HV represents evaporation latent heat of fluid, and VL represents tank volume of fluid.
The BOR of the tank was calculated using Equation (1), based on a thermal conductivity of 0.028 W/m·K[17], resulting in a BOR of 0.065%/day.
The values applied in the calculation are shown in Table 1, and the capacity of the evaporative gas treatment system was calculated by adding a 30% design margin, considering heat inflow from the pipe to the evaporative gas generation amount of 267.7 kg/h, resulting in 348.0 kg/h.
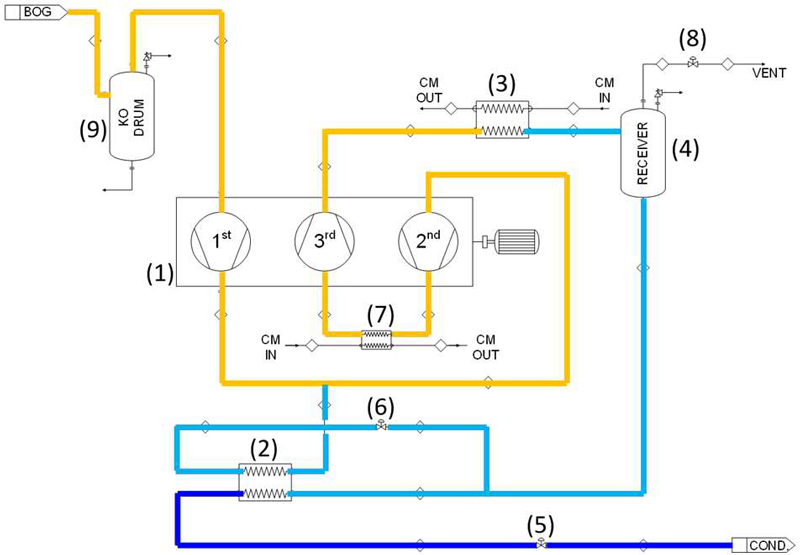
The configuration of ammonia BOG re-liquefaction process is as shown in Figure 1.
The evaporation gas generated from the fuel tank is supplied to the (1) compressor. At this time, a knockout drum (9) can be placed in front of the compressor to remove liquid droplets that may be contained in the evaporation gas. The compressor type is a three-stage reciprocating compressor, primarily used for ammonia and LPG carriers. Although the three-stage reciprocating compressor is more expensive compared to the screw type, it is widely used on actual ships because there is no contamination by lubricant in the gas handling system. The gas compressed in the first stage of the compressor is mixed with the side stream from the (2) heat exchanger and supplied to the second stage of the compressor. The side stream fluid is fed through (6) Joule-Thomson valve, resulting in additional cooling of the ammonia in the (2) heat exchanger. The subsequent expansion of the fluid through the (5) Joule-Thomson valve into the tank decreases the vapor fraction. The gas compressed in the second stage is supplied to the third stage of the compressor through (7) a heat exchanger for cooling the gas on the second stage discharge side. The pressurized gas in stage 3 is supplied to the (4) receiver tank through the (3) condenser. Cooling medium of the system is glycol water which is supplied from ship’s utility system. Ammonia supplied to the receiver tank is basically in a supercooled state, so no evaporation gas is generated, but gases generated by nitrogen, air, etc., are discharged through the pressure control valve (8).
2.2 HYSYS Modeling
The ammonia tank's BOG treatment system does not need to consider various substances and only needs to address the discharge of ammonia and a small amount of nitrogen that may be included during operation. Thus, the process system can be configured more simply than the LPG re-liquefaction system.
The coolant for cooling and condensing ammonia is 32°C seawater and 36°C glycol water. Since the amount of BOG that needs to be reliquefied is 348.0 kg/h and the flow rate is not large, glycol water was considered as the coolant, and the minimum approach temperature for the heat exchanger was used. When calculated at 3°C, ammonia could be cooled to 40°C in the condenser. The saturation pressure of ammonia at 40°C was 14.5 bar based on the application of the e-NRTL equation of state, which can be expressed as Equation (2) below [19][20].
| (2) |
Where γi represents activity coefficient of component i, τji represents interaction parameter for component between components j and i, xj represents Mole fraction of component j, Gji represents Gibbs energy of component j with respect to component i.
The Equation (2) provided is used to calculate the natural logarithm of the activity coefficient (ln γi) of component i in a multicomponent system. This equation is typically used in thermodynamic models to describe non-ideal behavior in liquid mixtures. Each term in the equation has a specific role in determining how the interactions between different components affect the activity coefficient of the component in question [20].
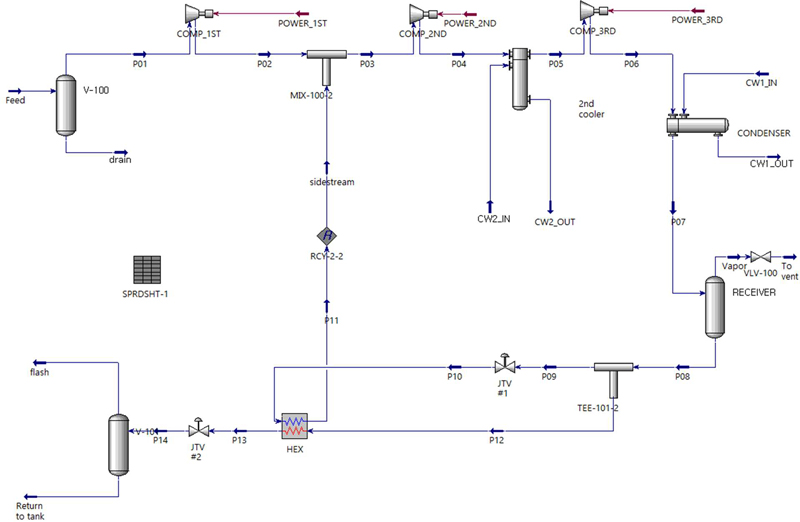
Discharge pressure of the compressor was 15.5 bar, considering the design margin. Applicable compressors include piston compressors, screw compressors, and turbo compressors. Piston compressor is applied, and it was determined that a three-stage compressor would be suitable since the compression ratio of the compressor to be applied is 16.3. The process system design is shown in Figure 2.
As shown, the evaporated gas generated in the fuel tank is routed to the compressor's suction side through a knockout drum and is then compressed to 15.5 bar using a three-stage compressor. The temperature of the side stream is 36°C, which means that the inlet of the second stage is above ambient temperature, necessitating the use of an intercooler at the discharge side of the second stage for cooling. The gas, compressed to 15.5 bar at the discharge side of the third stage, is then cooled and condensed to 40°C in the condenser.
2.3 Definition of Optimization and Determination of Variables
The fluid supplied to the target process is essentially pure ammonia, and any nitrogen component that may be included in the evaporative gas immediately after ammonia fuel bunkering is discharged during relatively short-term operation. Therefore, in this optimization program, which aims at optimizing steady-state operation, nitrogen was not considered as a variable. Based on the process system modeling results, the supply pressure for the evaporative gas treatment system was set to an initial value of 0.1 bar, and the discharge pressure was set to 15.5 bar. Efficiency-related variables of the process system, such as power consumption, cooling capacity, and the COP, are shown in Table 2.
In the ammonia re-liquefaction process, the optimization objective is defined as minimizing the total power consumption of the entire process required to reliquefy the evaporative gas generated in the tank. Therefore, the optimization objective function was set to power consumption. Accordingly, as shown in Table 3, the discharge pressure of each stage of the compressor and the flow rate of the side stream were selected as variables.
To perform optimization, it is important to set each variable of the system so that the process system can be practically implemented. For example, if the minimum temperature approach (MTA) of the heat exchanger is optimized to be below 3°C, the system efficiency may be high, but the heat transfer area of the heat exchanger might become too large, or it might be impossible to design the heat exchanger in practice. And log mean temperature difference (LMTD) has a limitation as well due to similar reason. Therefore, constant variables like MTA and LMTD are decided based on engineering practice. For cooling water, although lower temperatures can increase system efficiency, the cooling freshwater temperature available on the ship is 36°C, so consideration of the cooling water temperature is necessary. The compression ratio for each stage of the compressor was set to be 3 or less, and the outlet temperature of each stage was set to be below 170°C. The temperature of the evaporative gas supplied to the re-liquefaction system was set to -20°C, considering the saturation temperature of the fuel tank and the temperature rise in the main gas pipe. The related variables were set as constraint variables, and the input values for each constraint variable are shown in Table 4.
2.4 Determination of Optimization Method
This optimization problem is about finding the optimal values of decision variables that minimize or maximize an objective function under constraints. Constraints are conditions that the solution must satisfy, the objective variable is the target to be minimized or maximized, and decision variables are the variables whose values need to be determined.
- Black-box Optimization:The model to be optimized is configured based on the commercial simulation software Aspen HYSYS. The HYSYS tool itself inherently has several calculation functions capable of performing calculations related to heat, material, and energy. However, users cannot directly access the embedded equations nor obtain information about these equations, making it impossible to use them directly for optimization. Therefore, optimization of the target process becomes a type of optimization where some objective and constraint functions cannot be easily utilized, and the only information readily available to users is the output values for given input values. In other words, an optimization algorithm that only utilizes input and output values for calculations is needed for optimization.
- Optimization with Constraints:As mentioned earlier, there are several constraints associated with this process. In particular, the target process necessarily includes a heat exchanger, where physical constraints such as MTA and LMTD are typically used. These two constraints are the most important inequality constraints in this optimization and must be satisfied. Therefore, to find an optimal solution that does not violate these constraints, an algorithm capable of handling constraints is required. In this study, it was determined that applying the penalty function method, which converts constrained problems into unconstrained problems, is necessary.
In this paper, we used the Genetic Algorithm (GA), a method that represents possible solutions to the problem in a predefined data structure and gradually transforms them to produce increasingly better solutions, combined with the penalty function method.
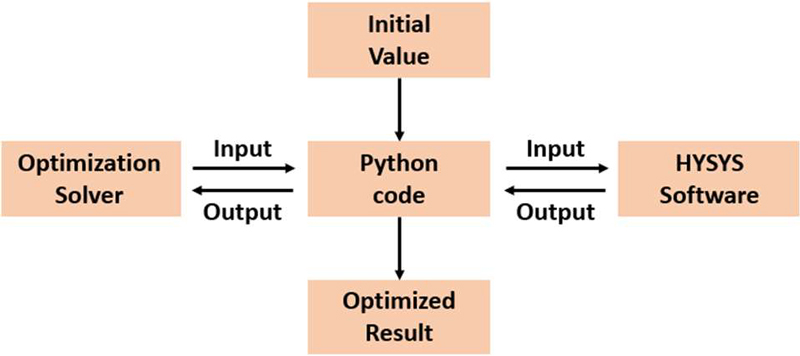
The structure of the optimization program, as shown in Figure 3, is based on the process of inputting initial values into the HYSYS model and running Python code. The Python code then sends these values as inputs to HYSYS and receives the calculation results as outputs.
The input and output values are handled by an optimization solver implemented in Python, which conducts the optimization process. Since continuous interaction with HYSYS is required to exchange input and output values, it is essential to maintain an organic connection with HYSYS and ensure that data is neither deleted nor lost. Once the optimal solution is obtained through the optimization solver, it is output along with the input and output values for each stage.
Optimization is implemented using Python as the programming language, with Python interfacing with Aspen HYSYS. After accessing the HYSYS library from Python to modify process variables, the modified HYSYS simulation results are read, and the optimization engine derives the next optimal point.
The optimization input and output interface is handled by Python code. By inputting the optimization variables into the Python code and executing it, the variables are entered into the Spreadsheet in HYSYS. After running the simulation, the optimization results are displayed in the Spreadsheet in HYSYS.
2.5 Development of Optimization Program
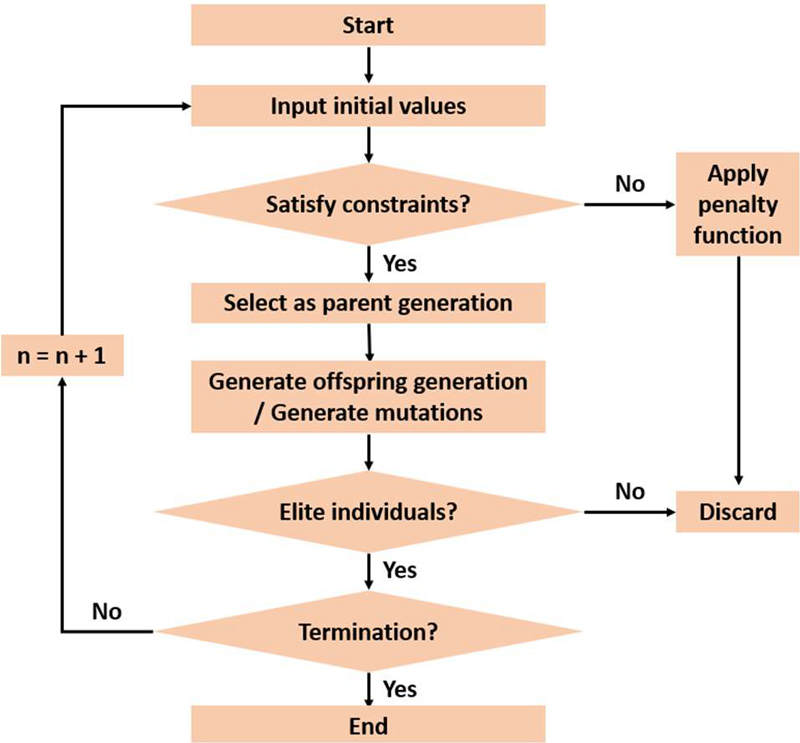
Figure 4 illustrates the flowchart of the ammonia re-liquefaction process optimization conducted in this study.
First, the initial values to be optimized are input into the HYSYS modeling file through Python code, and it is determined whether these initial values satisfy the constraints. If the initial point violates the constraints, a penalty function is applied to ensure that the result is not considered an optimal solution, thus discarding it [21][22].
The reason for checking whether the initial values satisfy the constraints is that the genetic algorithm applied in this study is a global optimization technique. It uses the given initial values to create new values through selection, crossover, and mutation, and the process is repeated with these new values as inputs. The penalty function is applied to initial values that violate constraints to discard them [23][24].
The initial values are used as input genes to create individuals, which are then evaluated for fitness. Individuals that pass the constraints are selected as the parent generation, and through the creation of offspring generation individuals, mutation of individuals, and selection of elite individuals, the optimal solution is determined.
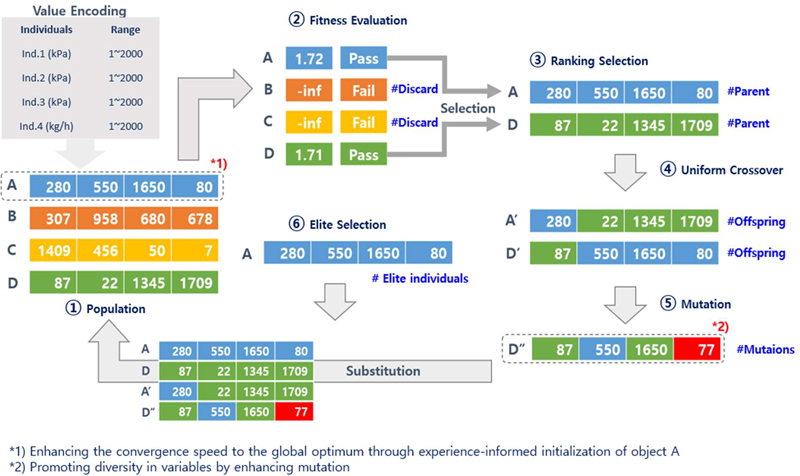
As shown in Figure 5, four individuals are created and evaluated for fitness. Only individuals A and D, which satisfy the constraints, are selected as the parent generation, while individuals B and C, which violate the constraints, are discarded. The parent generation individuals are crossed to create offspring individuals A and D, and some offspring are mutated to create mutated individual D”. The individuals generated so far constitute the first generation. Elite individuals are selected from the generated individuals and passed to the next generation. This process is repeated to find the optimal combination of variables.
During the creation of individuals, the range for each variable was set from 1 to 2000. The developer set the initial value for individual A based on the developer's experience in process system development, which helped improve the speed of finding a global solution. Additionally, a mutation rate of 40% was applied to provide ample opportunities for exploring global solutions.
To determine whether the variables and constraints are satisfied, a spreadsheet embedded in HYSYS was used. The coordinates of each cell in the spreadsheet were linked with Python code to facilitate input, output, and evaluation.
When each variable is input, the objective function calculation is performed in HYSYS. Since the developer does not know the calculation formulas, these are defined as black-box functions, and a method to compute the target values that meet the constraints is applied. In this process, hyperparameters corresponding to the number of generations, crossover, and mutation probabilities for running the genetic algorithm were set as shown in Table 5.
When the constraints are exceeded or an error occurs that prevents calculation results from being obtained, the penalty function method is used to apply a value of negative infinity to the output values, thus excluding them.
The optimal combination of variables is found, and hyperparameters are applied to select the optimal individuals among those generated. Based on the mutation probability, genes are modified to create new offspring generations, and the process is repeated with increasing generations to find the optimal individual. Among the individuals in each generation, including parent generation, offspring generation, and mutated individuals, the combination of variables with the best objective function is selected as the elite individual. This elite individual is then used as the parent for the next generation, and the process is repeated.
3. Result and Discussion
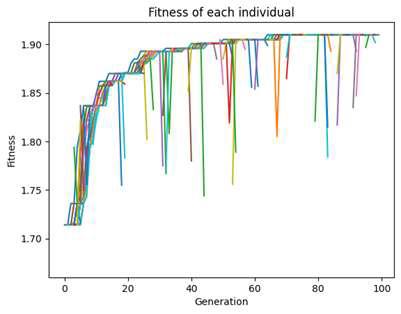
When the number of generations was set to 100 and the optimization code was executed, a local solution close to the first global solution was found at the 60th generation, and the program terminated normally after running through 100 generations. Due to the nature of the optimization code, individuals that violate constraints are expected to be discarded in each generation. As shown in Figure 6, it was observed that even with successive generations, there were continuously discarded individuals. Additionally, the distribution of fitness across generations showed that, despite the increasing number of generations, the global solution was consistently found, and fitness rankings improved, indicating that the elite individuals were selected and applied as parents for the next generation.
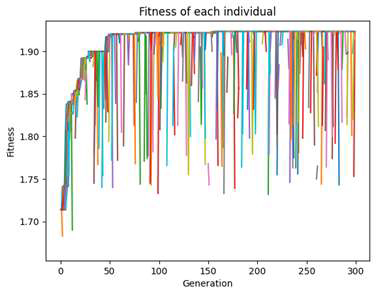
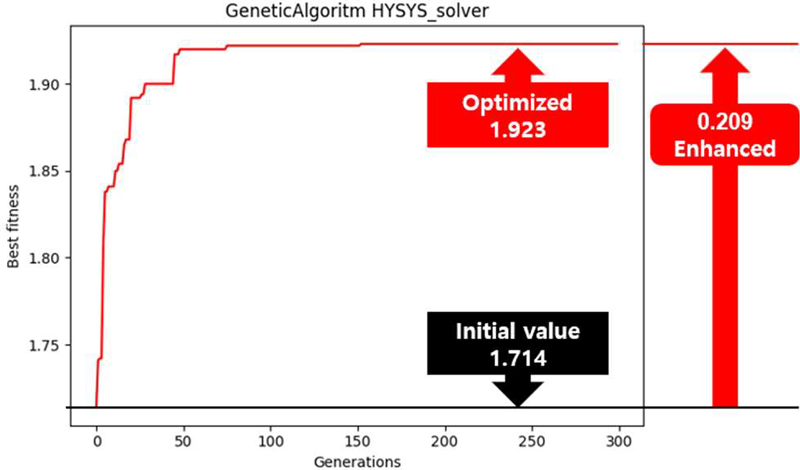
It was observed that the fitness level increased at the 100th generation, leading to the conclusion that the optimal solution obtained at 100 generations was not the global optimum. Therefore, the number of generations was increased to 300 and the code was executed again. As with the previous run, a local solution close to the global optimum was found at the 60th generation, and the program terminated normally after running through 300 generations.
As shown in Figure 7, it was confirmed that the penalty function and elite individual selection were functioning correctly.
The optimized COP was 1.923, which represents an improvement of 0.209 compared to the initial value, indicating a 12.2% enhancement. The program ran for 19,415 seconds over 300 generations. At this point, the discharge pressures of the compressor were 210 kPa for the first stage, 630 kPa for the second stage, and 1,555 kPa for the third stage, with a side stream flow rate of 81 kg/h, resulting in a COP of 1.923.
In the ammonia re-liquefaction process, the optimization goal was set to the COP of the process system. Since nitrogen, a possible impurity in the BOG, is expelled during the early operation of the process system, it was not considered as a variable in the optimization program aimed at steady-state operation. The composition of the BOG was assumed to be 100% ammonia.
Using the genetic algorithm as the primary method, an optimization code was executed applying penalty functions and elite individual selection. The algorithm effectively converged to a nearglobal optimum within 60 generations, as shown in Figure 8. Subsequent generations exhibited negligible fitness improvements among elite individuals, confirming convergence after 150 iterations. Notably, enhancing the convergence speed towards the global optimum was achieved through experience-informed initialization of the first-generation population and increased variable density via mutation.
Therefore, the COP obtained after running 300 generations was considered the global optimum. At this point, the optimal values for the variables and objective function are as follows: first-stage discharge pressure of 210 kPa, second-stage discharge pressure of 630 kPa, third-stage discharge pressure of 1,555 kPa, side stream flow rate of 81 kg/h, and a COP of 1.923. When converted to bar units, these values are shown in Table 6.
4. Conclusion
To optimize the BOG re-liquefaction system of an ammonia fueled ship, a process system model was developed using HYSYS, and a study was conducted to improve system efficiency through optimization. An analysis of the steady-state modeling was performed, and the definition of optimization was established. Variables for optimization were analyzed, and optimal values for these variables were derived to optimize the objective function of the target process system through the implementation of an optimization solver.
An optimization tool was developed using Genetic Algorithm and Penalty Function methods. This tool was developed such that initial values were input into the HYSYS model, and when the Python code was executed, it sent these values as inputs to HYSYS and received the calculation results as outputs.
Before optimization, the COP based on the initial input values was 1.714. After performing optimization over 300 generations using the algorithm, the COP achieved was 1.923, resulting in an approximate 12% improvement in COP, assuming all variables are applicable to the actual process system. However, this study does not fully address the practical challenges associated with implementing the optimized BOG re-liquefaction system in ammonia fueled ship. Issues such as system integration with existing ship system, maintenance requirements, and operational flexibility require further investigation, which will be the focus of future work.
Nomenclature
| bar : | bar gauge |
| G : | Gibbs energy of a component |
| γ : | Activity coefficient of component |
| HV : | Evaporation latent heat of fluid |
| Q : | Total heat flow rate |
| ρ : | Density of fluid |
| τ : | Interaction parameter for component between two components |
| VL : | Tank volume of fluid |
| x : | Mole fraction of component |
| γ : | Activity coefficient of component |
Abbreviation
| BOG : | Boil-off gas |
| BOR : | Boil-off rate |
| COP : | Coefficient of performance |
| GA : | Genetic algorithm |
| HFO : | Heavy fuel oil |
| IMO : | International maritime organization |
| LMTD : | Log mean temperature difference |
| LNG : | Liquefied natural gas |
| MCR : | Maximum continuous rating |
| MDO : | Marine diesel oil |
| MEPC : | Marine environment protection committee |
| MGO : | Marine gas oil |
| MTA : | Minimum temperature approach |
| NCR : | Normal continuous rating |
| PIR : | Polyisocyanurate |
| PUF : | Polyurethane foam |
| VLCC : | Very large crude carrier |
Author Contributions
Conceptualization, S. K. Jeong and Y. T. Kim; Methodology, S. K. Jeong and J. S. Kim; Software, S. K. Jeong and J. S. Kim; Formal Analysis, S. K. Jeong and J. S. Kim; Investigation, S. K. Jeong; Resources, S. K. Jeong; Data Curation S. K. Jeong; Writing-Original Draft Preparation, S. K. Jeong; Writing-Review & Editing, Y. T. Kim and J. S. Kim; Visualization, S. K. Jeong; Supervision, Y. T. Kim and J. S. Kim.
References
-
J. R. Smith and E. Mastorakos, “A systems-level study of ammonia and hydrogen for maritime transport,” Maritime Transport Research, vol. 5, 100099, 2023.
[https://doi.org/10.1016/j.martra.2023.100099]

- IMO, Initial IMO Strategy on Reduction of GHG Emis-sions from Ships, Resolution MEPC.304(72) (Adopted on 13 April 2018), MEPC 72/17/Add.1, 1–10, 2018.
-
K. Bayramoğlu, “The effects of alternative fuels, cruising duration and variable generators combination on exhaust emissions, energy efficiency existing ship index (EEXI) and carbon intensity rating (CII),” Ocean Engineering, vol. 302, 117723, 2024.
[https://doi.org/10.1016/j.oceaneng.2024.117723]

-
H. Jang, M. P. Mujeeb-Ahmed, H. Wang, C. Park, I. Hwang, B. Jeong, P. Zhou, and R. Mickeviciene, “Regula-tory gap analysis for risk assessment of ammonia-fuelled ships,” Ocean Engineering, vol. 287, Part 2, 115751, 2023.
[https://doi.org/10.1016/j.oceaneng.2023.115751]

-
H. Xing, C. Stuart, S. Spence, and H. Chen, “Alternative fuel options for low carbon maritime transportation: Path-ways to 2050,” Journal of Cleaner Production, vol. 297, 126651, 2021.
[https://doi.org/10.1016/j.jclepro.2021.126651]

-
M. Bayraktar, “Investigation of alternative fuelled marine diesel engines and waste heat recovery system utilization on the oil tanker for upcoming regulations and carbon tax,” Ocean Engineering, vol. 287, Part 1, 2023.
[https://doi.org/10.1016/j.oceaneng.2023.115831]

-
A. Al-Enazi, E. C. Okonkwo, Y. Bicer, and T. Al-Ansari, “A review of cleaner alternative fuels for maritime transpor-tation,” Energy Reports, vol. 7, pp. 1962-1985, 2021.
[https://doi.org/10.1016/j.egyr.2021.03.036]

-
S. Lagouvardou, H. N. Psaraftis, and T. Zis, “A literature survey on market-based measures for the decarbonization of shipping.” Sustainability, vol. 12, no. 10, 2020.
[https://doi.org/10.3390/su12103953]

-
M. Prussi, N. Scarlat, M. Acciaro, and V. Kosmas, “Poten-tial and limiting factors in the use of alternative fuels in the European maritime sector,” Journal of Cleaner Production, vol. 291, 2021.
[https://doi.org/10.1016/j.jclepro.2021.125849]

-
H. Mun, H. Kim, J. Park, and I. Lee, “A novel boil-off gas reliquefaction system using liquid air for intercontinental liquefied natural gas transportation,” Energy Conversion and Management, vol. 269, 2022.
[https://doi.org/10.1016/j.enconman.2022.116078]

- DNV, Maritime Forecast to 2050, Energy Transition Out-look 2022, 2022.
- Bureau Veritas, An overview of alternative fuels from a well-to-wake perspective, White paper, Alternative fuels outlook for shipping, 2022.
- MAN Diesel & Turbo, Propulsion of 7,000-10,000 dwt, Propulsion of 46,000-50,000 dwt, Propulsion of VLCC, 2013.
- MAN Diesel & Turbo, Propulsion of VLCC, 2016.
- WinGD, GTD – General Technical Data for WinGD 2-Stroke Engines, 2024.
- Babcock LGE, Process Manual 13033-PM-13-015-01, 2017.
-
M. Gravit, A. Kuleshin, E. Khametgalieva, and I. Karako-zova, “Technical characteristics of rigid sprayed PUR and PIR foamsused in construction industry,” IOP Conference Series: Earth and Environmental Science, vol. 90, 2017.
[https://doi.org/10.1088/1755-1315/90/1/012187]

-
A. Vorkapić, P. Kralj, and D. Martinović, “The analysis of the maintenance systems of a LPG carrier’s liquefaction system main components,” Scientific Journal of Maritime Research, vol. 31, 2017.
[https://doi.org/10.31217/p.31.1.2]

-
Kh. Mejbri and A. Bellagi, “Modelling of the thermodynam-ic properties of the water–ammonia by three different ap-proaches” International Journal of Refrigeration, vol. 29, no. 2, pp. 211-218, 2006.
[https://doi.org/10.1016/j.ijrefrig.2005.06.002]

-
M. Sibhat, Q. Zhu, G. Tsegay, G. Yao, G. Yin, Y. Zhou, and J. Zhao, “Enhancement technologies of ammonia-based carbon capture: A review of developments and challenges,” International Journal of Greenhouse Gas Control, vol. 136, 2024.
[https://doi.org/10.1016/j.ijggc.2024.104196]

- A. E. Smith and D. W. Coit, Penalty Functions, A Joint Publication of Oxford University Press and Institute of Physics Publishing, 1995.
- Shunji Umetani, Learning Mathematical Optimization Properly: From Optimization Modeling to Algorithm, Shik-kari manabu suuri saitekita model kara algorithm made, 2022 (in Korean).
- Mathematical optimization: Genetic algorithm and global optimization, https://untitledtblog.tistory.com/110, , Accessed June 16, 2024.
- Data science and optimization: Genetic algorithm, https://gils-lab.tistory.com/29, , Accessed June 16, 2024.