Consideration on the control characteristics of active rectifier for shaft generator through comparison with a diode rectifier
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In response to the increasingly stringent CO2 reduction strategies by the International Maritime Organization (IMO), active development of technologies is underway, among which the shaft generator system is emerging as the most realistic energy efficiency improvement technology with rapidly growing demand. Since the shaft generator shares its shaft with the ship's main engine, a shaft generator drive is necessary to stably integrate fluctuating output voltage and frequency into the power system. Controlling the direct current (DC) voltage of the drive is crucial for enhancing the quality of power during system integration. Recently, active rectifier utilizing power semiconductors have been applied for this purpose. In this paper, perform a comparative simulation using Matlab/Simulink to analyze the control and output characteristics of active rectifiers, under conditions identical to those of diode rectifiers. The results demonstrate that active rectifiers can maintain the commanded voltage despite fluctuations in the input voltage and frequency of the shaft generator and keep the voltage ripple rate within 1%, showing superior output characteristics compared to diode rectifiers.
Keywords:
Shaft generator, Direct current voltage control, Active rectifier, Shaft generator drive, CO2 reduction technology1. Introduction
The intensification of carbon dioxide reduction regulations by the International Maritime Organization (IMO) has spurred active development in technologies aimed at reducing carbon emissions from ships [1]-[3]. Achieving zero carbon emissions from ships ultimately necessitates the use of carbon-free fuels such as hydrogen and ammonia. However, current limitations in fuel supply and pricing pose significant challenges [4]. Consequently, research is being conducted on the application of energy efficiency improvement technologies as a practical alternative [5].
The shaft generator, a commercialized energy efficiency technology, has seen a surge in demand for maritime applications due to its proven effectiveness [6]. This technology harnesses the torque of a ship's propulsion engine to generate electricity. As the rotor shaft of the generator shares its axis with the propeller shaft, changes in the rotational speed of the propulsion engine directly affect the output voltage and frequency of the shaft generator. To align with the ship's power system voltage and frequency, a shaft generator drive is installed at the output end of the generator. This drive modulates the power input from the shaft generator to match the power system's voltage and frequency, facilitating integration.
The importance of maintaining a precise DC voltage level in shaft generator drives to improve the quality of power integrated into the ship's power system.[7] It highlights the necessity of not only sustaining the commanded voltage but also minimizing the ripple component in the DC link.[8] These factors are critical for ensuring the efficient and reliable operation of the power system on maritime vessels [9].
This paper focuses on the critical role of the direct current (DC) voltage level in the shaft generator drive for improving the quality of power integrated into the ship's system. Maintaining a commanded voltage and minimizing ripple components are essential for optimal performance. The study employs Matlab/Simulink to compare the outcomes of applying power semiconductors in an Active Rectifier and a diode-type rectifier under identical shaft generator and load conditions. The analysis reveals the control characteristics of the Active Rectifier, along with its impact on voltage ripple and voltage fluctuations.
2. Rectifier for Shaft Generator Drive
2.1 Layout for Shaft Generator System
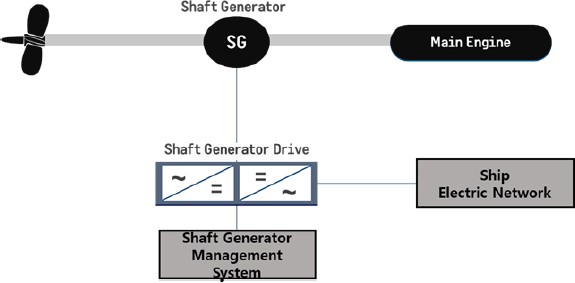
As shown in Figure 1, the shaft generation system comprises the Shaft Generator, Shaft Generator Drive (SGD), and Shaft Generator Management System. The Shaft Generator transmits the power generated by the torque of the propulsion engine to the ship's power system through the SGD. The Shaft Generator Management System communicates data with the Engine Control System (ECS) and the ship's power management system, and delivers commands to the SGD regarding active and reactive power.
2.2 Shaft Generator System of Vessel
The shaft generator is mechanically coupled with the propulsion engine's shaft, resulting in the rotor of the shaft generator rotating at the same rotational speed as the propulsion engine. The output frequency is determined as shown in Equation (1), where rpm represents the revolutions per minute of the shaft generator, f denotes frequency, and P indicates the number of poles [10].
| (1) |
Additionally, the output voltage of the shaft generator is determined according to Equation (2), where E represents the voltage, N is the number of turns, Φ denotes the flux, and Kw is the winding coefficient [10].
| (2) |
As can be seen from Equation (2), the number of turns and the winding coefficient in the output voltage equation of the shaft generator are constants determined during the manufacturing of the generator. As per Equation (1), the frequency varies with the rotational speed of the shaft generator. Therefore, the only adjustable parameter for controlling the output voltage is the magnitude of the flux. In the case of synchronous generators with exciters, the output voltage can be regulated by varying the flux magnitude. However, for induction or permanent magnet type shaft generators, the flux magnitude cannot be separately adjusted, so the output voltage is determined by the rotational speed of the shaft.
2.3 Rectifier for Shaft Generator Drive
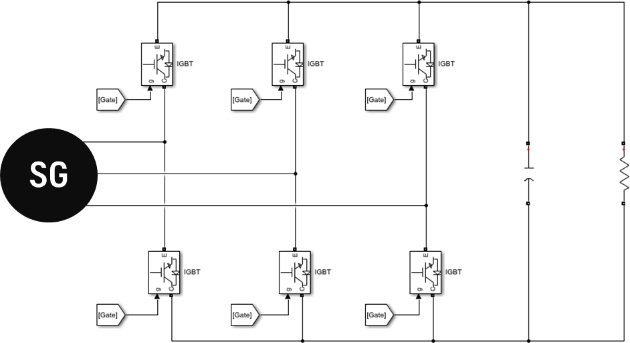
The shaft generator drive primarily consists of a rectifier section and an inverter section in Figure 2. The rectifier section converts the power input from the shaft generator into direct current (DC) using either a diode rectifier or an Active Rectifier. If the system operates on DC, the Shaft Generator Drive (SGD) is composed solely of the rectifier section. In cases where the system is alternating current (AC), an inverter section is additionally included. This inverter section adjusts the output to match the voltage and frequency of the ship's power system through the switching of power semiconductors.
A diode rectifier primarily serves the purpose of rectifying current and, therefore, cannot regulate the magnitude of the direct current (DC) link voltage. The magnitude of the DC link voltage is determined by the size of the input voltage. Equation (3) represents the DC link voltage for a 6-Pulse rectifier, where Vdc is the DC link voltage and Vll is the input line-to-line voltage.
| (3) |
The Active Rectifier utilizes active components such as IGBTs (Insulated Gate Bipolar Transistors), IGCTs (Integrated Gate-Commutated Thyristors), or MOSFETs (Metal-Oxide-Semiconductor Field-Effect Transistors), instead of diode elements, allowing for direct control of the output voltage through switching [11]. The drive's DC link voltage is measured and compared with a reference voltage. By directly controlling the switching elements, the DC link voltage can be maintained at the desired level. Figure 3 illustrates the configuration of an Active Rectifier.
3. System Modeling
3.1 Simplified Shaft Generator
Based on Equations (1) and (2), a model of a permanent magnet type shaft generator, whose voltage and frequency vary with changes in the speed of the propulsion engine, was developed. This model takes the rotational speed of the propulsion engine as input and outputs three-phase voltage and frequency. It was constructed using the Matlab function block and libraries in Matlab Simulink, as illustrated in Figure 4.
The output frequency is given by Equation (4), where rpm curr represents the real-time input parameter, and rated rpm refers to the rated revolutions per minute.
| (4) |
The instantaneous maximum of the three-phase voltage, denoted as Vmax , is given by Equation (5).
| (5) |
The magnitude of the three-phase voltage is expressed as per Equations (6), (7), and (8).
| (6) |
| (7) |
| (8) |
The parameters for this model and the Shaft Generator are as presented in Table 1.
3.2 Active Rectifier
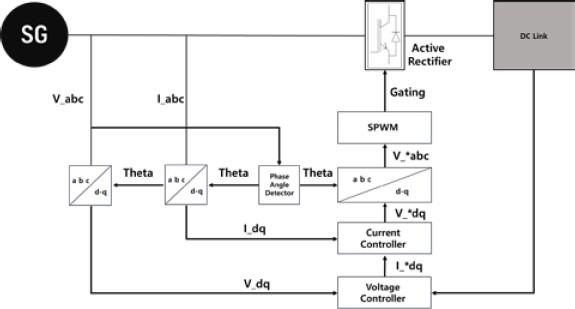
Figure 5 illustrates the control block diagram for a three-phase active rectifier. The system measures the output voltage and current of the shaft generator, as well as the voltage at the DC link. It then controls the switching elements through a control system that follows the command voltage set point for the DC link.
The relationship between the output voltage of the shaft generator and the input voltage of the converter is given by Equation (9).
| (9) |
This relationship is transformed into a two-phase direct current component on the dq-axis, and when organized according to the three-phase balanced condition for the converter input voltage, it results in Equations (10) and (11).
| (10) |
| (11) |
The PWM (Pulse Width Modulation) voltage command for the converter, which utilizes a PI (Proportional-Integral) current controller, is defined by Equations (12) and (13).
| (12) |
| (13) |
The d-axis current command with the applied PI voltage controller is given by Equation (14).
| (14) |
Based on the rated output, voltage, and DC command voltage of the shaft generator, an LCL filter was designed to reduce power noise and harmonics [12]. The related parameters are as presented in Table 2.
3.3 DFE Rectifer
For comparison with the Active Rectifier, a Diode Rectifier was set up as shown in Figure 6, with an inductor and a capacitor applied on the load side.
In the absence of a filter under full load, approximately 13% voltage ripple occurred. To reduce this to within 2%, an inductor and capacitor were designed based on the parameters listed in Table 3 [13].
4. Simulation
4.1 Shaft Generator Operation Scenario for Simulation
To evaluate the control and output characteristics of the Active Rectifier in comparison with the Diode Rectifier, a simulation was conducted by linearly decreasing the speed of the shaft generator from 100% to 60% of its rated speed over a period of 10 seconds, as outlined in Table 4.
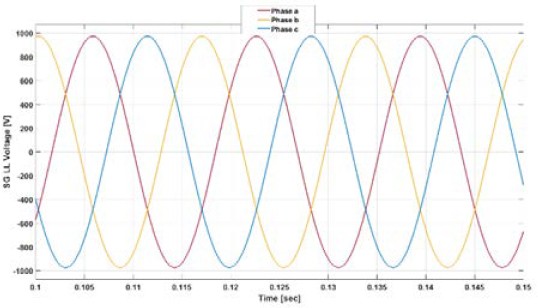
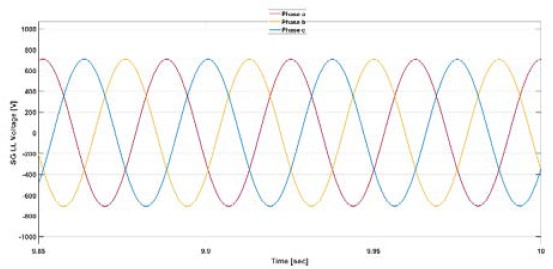
The voltage values input to both the Diode Rectifier and Active Rectifier were monitored in accordance with the SG rpm variation scenario. Figure 7 shows the SG voltage output at rated conditions, while Figure 8 displays the voltage output at 60% of the rated conditions.
As shown in Figures 7 and 8, it can be observed that the shaft generator (SG) outputs a voltage of 690V at its rated speed and 500V at 1080 rpm. This demonstrates that the output voltage varies in accordance with changes in speed.
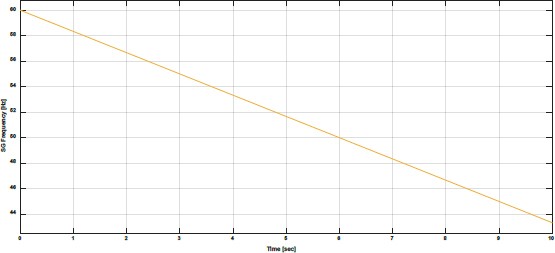
Figure 9 presents a graph of the output frequency as it changes with the SG's rotational speed. It can be seen that the frequency also changes in proportion to the linear decrease in speed.
4.2 Comparison of Output Voltage for Active Rectifier and Diode Rectifier
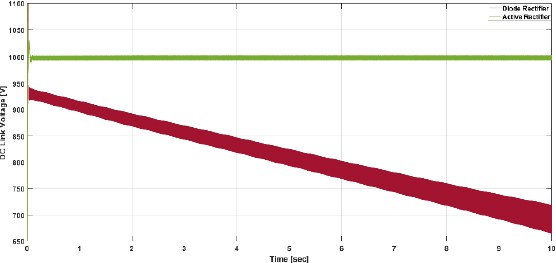
Figure 10 presents the DC Link graphs for both the Diode Rectifier and the Active Rectifier. In the case of the Diode Rectifier, as the three-phase input voltage decreases, the output voltage also decreases correspondingly. In contrast, the Active Rectifier continuously maintains the commanded voltage of 1000V.
Figure 11 shows a graph representing the DC Link output voltage ripple during the initial 0.1 to 0.2 seconds of the simulation when the rated voltage of the shaft generator is applied to the rectifier. The Diode Rectifier exhibits a voltage fluctuation between 919.7 and 938.5 [V], with a ripple rate of about 2.02%, while the Active Rectifier shows a voltage fluctuation between 994 and 1003 [V], resulting in a ripple rate of approximately 0.90%.
Figure 12 depicts the DC Link output voltage ripple during the period between 9.8 and 10.0 seconds in the simulation, when the rpm and output voltage of the shaft generator are reduced by 40% and applied to the rectifier. The Diode Rectifier shows a voltage fluctuation between 667.3 and 721.3 [V] with a ripple rate of about 7.78%, whereas the Active Rectifier exhibits a voltage fluctuation between 993.7 and 1002.9 [V], resulting in a ripple rate of approximately 0.92%. The ripple rate of the Diode Rectifier increases by 5.76% compared to the rated input voltage, while the Active Rectifier shows a minor increase of 0.02%, indicating negligible difference despite the input voltage variations.
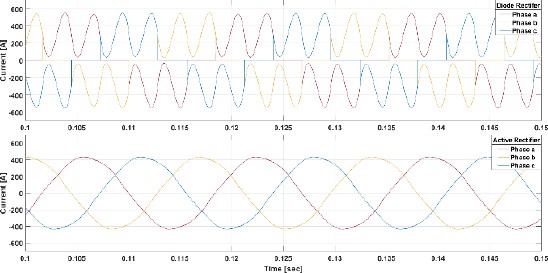
Figure 13 presents a graph of the three-phase current of the shaft generator during the initial 0.1 to 0.15 seconds of the simulation. When the Diode Rectifier is used, distortion in the current waveform results in an output that is not a normal sine wave. However, with the Active Rectifier applied, the current waveform of the shaft generator is observed to be closely resembling a sine wave.
Figure 14 illustrates a graph showing the output current waveform of the shaft generator at 60% of the rated revolutions per minute (rpm). Similar to the findings at the rated condition, it is observed that the current output waveform of the Diode Rectifier is not a stable sine wave.
5. Conclusion
Recently, there has been a rapid increase in the application of shaft generation systems in ocean-going vessels directly addressing the International Maritime Organization (IMO) GHG reduction regulations. Especially with the adoption of permanent magnet or induction type shaft generators, where the output voltage is determined by the rotational speed of the main engine, the importance of rectifiers for DC voltage control in shaft generator drives has become more significant.
In this paper, a comparative simulation of the Diode Rectifier and Active Rectifier under identical conditions was conducted to analyze the voltage control characteristics and output voltage ripple rate of the Active Rectifier. The Active Rectifier was found capable of maintaining the DC voltage in line with the reference voltage despite input voltage variations from the shaft generator, and keeping the voltage ripple rate within 1%. In contrast, the DC link voltage of the Diode Rectifier varied with input voltage fluctuations, and the ripple rate increased by more than 5% compared to the rated frequency.
For most ships with AC systems, employing an Active Rectifier can ensure system stability as it can maintain a constant drive DC link despite output fluctuations of the shaft generator. In the case of drives using Diode Rectifiers, additional measures for DC link voltage stabilization during low-speed operation of the shaft generator and precise control of the inverter section for system integration may be required.
Acknowledgments
This research was supported by Korea Evaluation Institute of Industrial Technology(KEIT) funded by the Ministry of Commerce Industry and Energy(RS-2022-00144151).
Author Contributions
This research presented in this paper was wholly contributed by the Corresponding Author.
References
-
G. Mallouppas and E. A. Yfantis, “Decarbonization in shipping industry: A review of research, technology development, and innovation proposals,” Journal of Marine Science and Engineering, vol. 9, no. 4, p. 415, 2021.
[https://doi.org/10.3390/jmse9040415]

-
P. Balcombe, J. Brierley, C. Lewis, L. Skatvedt, J. Speirs, A. Hawkesa, and I. Staffell, “How to decarbonise international shipping: Options for fuels, technologies and policies,” Energy Conversion and Management, vol. 182, pp. 72-88, 2019.
[https://doi.org/10.1016/j.enconman.2018.12.080]

-
H. M. Kim, H. Jeon, K. Yoon, and J. S. Kim, “Study on the simulation of the dynamic characteristics of a marine diesel generator,” Journal of Advanced Marine Engineering and Technology, vol. 45, no. 6, pp. 392-397, 2021.
[https://doi.org/10.5916/jamet.2021.45.6.392]

-
Y. Wang, Q. Cao, L. Liu, Y. Wu, H. Liu, Z. Gu, and C. Zhu, “A review of low and zero carbon fuel technologies: Achieving ship carbon reduction targets,” Sustainable Energy Technologies and Assessments, vol. 54, 2022.
[https://doi.org/10.1016/j.seta.2022.102762]

-
J. Hüffmeier and M. Johanson, “State-of-the-art methods to improve energy efficiency of ships,” Journal of Marine Science and Engineering, vol. 9, no. 4, p. 447, 2021.
[https://doi.org/10.3390/jmse9040447]

-
J. Prousalidis, C. Patsios, F. Kanellos, A. Sarigiannidis, N. Tsekouras, and G. Antonopoulos, “Exploiting shaft generators to improve ship efficiency,” Electrical Systems for Aircraft, Railway and Ship Propulsion, pp. 1-6, 2012.
[https://doi.org/10.1109/ESARS.2012.6387443]

-
R. K. Gaddala, M. G. Majumder, and K. Rajashekara, “DC-link voltage stability analysis of grid-tied converters using DC impedance models,” Energies, vol. 15, no. 17, p. 6247, 2022.
[https://doi.org/10.3390/en15176247]

-
M. Vujacic, M. Hammami, M. Srndovic, and G. Grandi, “Analysis of dc-link voltage switching ripple in three-phase PWM invertes,” Energies, vol. 11, no. 2, p. 471, 2018.
[https://doi.org/10.3390/en11020471]

-
K. K. Yoon, “Study on verification of AFE rectifier control for electric propulsion ship,” Journal of Advanced Marine Engineering and Technology, vol. 45, no. 6, pp. 402-410, 2021.
[https://doi.org/10.5916/jamet.2021.45.6.402]

- S. H. Kim, J. S. Kim, S. J. Oh, and H. S. Kim, Practical Electrical Machinery, Seoul, Korea: Seonandang, 2011 (in Korean)
-
J. J. Hur, K. W. Kang, J. S. Kim, and S. H. Kim, “Speed control for direct current motor using an AFE rectifier,” Journal of the Korean Society of Marine Engineering, vol. 42, no. 10, pp. 829-835, 2018.
[https://doi.org/10.5916/jkosme.2018.42.10.829]

-
S. G. Seo, Y. C, and K. B. Lee, “Design of an LCL-Filter for space vector PWM in a grid-connected system,” The Transactions of the Korean Institute of Power Electronics, vol. 21, no. 6, pp. 538-541, 2016.
[https://doi.org/10.6113/TKPE.2016.21.6.538]

-
X. Du, L. Zhou, H. Lu, and H. M. Tai, “DC link active power filter for three-phase diode rectifier,” IEEE Transactions on Industrial Electronics, vol. 59, no. 3, pp. 1430-1442, 2012.
[https://doi.org/10.1109/TIE.2011.2167112]