Designing container crane control learning model using deep learning
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Ports are crucial infrastructure in the global supply chain, and the digitalization and automation of ports have been recently promoted worldwide. Container terminals face increasing competition owing to expanding ships and increasing container throughput. Quay area container cranes are the key equipment for container loading and unloading; however, their level of automation is lower than those of yard cranes and automated guided vehicles (AGVs). Additionally, they have persistent issues such as variations in work speed depending on the operator's skill, potential human error, and the time and cost required for training and education to generate skilled personnel. This study designed a deep learning-based container crane control model to predict the input force values applied to the trolley and hoist to move a container to the target position, when its initial position, target position, and weight are provided. We designed a container crane simulator that emulates a skilled operator handling a container. Data on the trolley and hoist force values were collected for 1,008 cases with different initial positions, target positions, and weights. The recurrent neural network, long short-term memory, and gated recurrent unit (GRU) models were designed to learn the relationship between the target trajectory of the container and the input force values of the trolley and hoist. These values were predicted for three different vessel operation scenarios with different initial positions, target positions, and weights to evaluate the model performance. The GRU container crane control learning model exhibited high prediction accuracy for the input force values of the trolley and hoist. A dynamic simulation confirmed that the container crane could be controlled to move from the initial to the target position.
Keywords:
Automated container terminal, Container crane automation, Deep learning, LSTM, GRU, Force prediction1. Introduction
While ports have traditionally been considered as the elements of the global supply chain, recent uncertainties in external conditions have caused a paradigm shift, identifying ports as a critical infrastructure. As a pivotal junction between maritime and inland transportation, ports are crucial in the overall operation of the global supply chain. The global smart port market is projected to grow from $19 billion in 2022 to $57 billion in 2027 [1].
Major ports worldwide have embraced the digitization, automation, and smartification of their operations. Port automation, a key aspect of smart ports, is mainly applied to container terminals. Domestically, container terminals have witnessed a rapid increase in yard occupancy rates owing to the enlargement of vessels and inadequate berth conditions caused by rising container traffic. Furthermore, the emergence of Northeast Asia as the epicenter of global trade has intensified the competition among nations, including China, to rapidly expand port facilities. To secure a competitive edge, global terminal operators continuously invest in various technologies based on the Fourth Industrial Revolution, aiming to optimize operational systems and automate equipment to enhance productivity.
The competitiveness of container terminals depends on the speed of processing the containers to increase productivity. This involves handling containers from the ship to the quay or viceversa, and the equipment responsible for transferring containers between the quay and yard. Current automation technologies for container terminals focus on automating yards and transferring operations to ensure seamless coordination.
However, the automation level of container cranes, a critical component of quay areas, remains relatively inadequate. While attempts have been made to automate the loading and unloading operations using container cranes, the complete exclusion of human operators has not been achieved. Currently, operators either board the crane cabin directly or control the trolley and hoist remotely from a control room. Consequently, the task is subject to variations in the operation speed based on the operator's proficiency. However, human error is probable, and the time and cost constraints associated with the training of skilled operators pose significant limitations. These challenges affect the productivity of container terminals and the dwell time of vessels in ports. Thus, crane automation is crucial, necessitating innovative technologies and solutions to overcome these limitations.
Existing studies on cranes can be categorized into dynamic modeling performed in three-dimensional space and control model design to minimize the sway and energy consumption during cargo movement. Yu et al. [2] proposed a composite nonlinear feedback control for overhead cranes to improve the crane control performance and stability. Furthermore, Ismail et al. [3] introduced sliding mode control to ensure control performance and robustness in the presence of external interference during maritime container crane operations. Lu et al. [4] presented a path-planning method for minimizing energy consumption while controlling the horizontal motion of a double-pendulum crane system.
Although these research efforts have focused on minimizing cargo sway, skewness, and energy consumption, studies related to models that learn crane control methods for moving cargo, such as containers, to specific locations are limited. This study addresses this gap by developing a learning model to predict the input forces on the trolley and hoist that shift containers of various weights from their initial positions to target locations when both these positions are provided.
The remainder of this paper is organized as follows: Section 2 briefly describes the container crane and its dynamic model used in this study. Section 3 discusses the design of the proposed container crane control learning model using deep learning. Section 4 uses simulation to evaluate the prediction results of the designed recurrent neural network (RNN), long short-term memory (LSTM), and gated recurrent unit (GRU) models. Section 5 concludes the study.
2. Theoretical Background
2.1 Container Crane
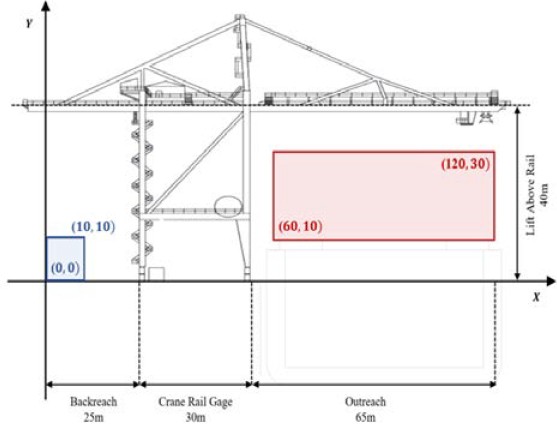
Container cranes, also known as quay or ship-to-shore cranes, are container-handling equipment employed in loading and unloading operations (vessel operations) when a container vessel docks at a terminal. These cranes facilitate the transfer of containers between the vessel and berth. Their productivity, which is a crucial component of container terminals, is measured as the number of containers handled per hour. These cranes can process between 25 and 30 containers per hour—a metric that significantly influences the overall productivity of a container terminal.
The container crane structure comprises the crane body, which moves along the rails installed on the apron, a folding boom extending from the body toward the vessel, girders extending from the body toward the apron, a trolley for the horizontal movement along the installed rails, a hoist connected to the trolley for the vertical movements of containers, a control room, and devices, such as spreaders, attached to the end of the hoist rope for lifting and lowering containers.
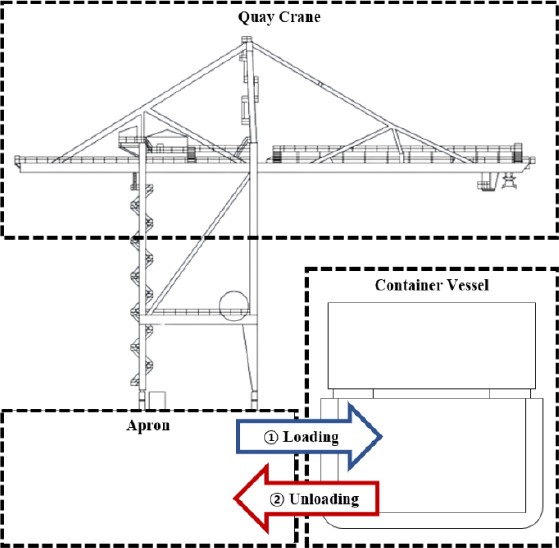
Figure 1 shows the layout of the quay area where vessel operations using container cranes occur. The container crane transfers the containers from the yard to the apron before lifting and moving them toward the vessel. Thereafter, the crane performs loading operations by lowering the containers to specified locations within the vessel or unloading operations by picking up containers from the vessel, moving them toward the apron, and lowering them to their designated positions on the apron or waiting transport vehicles. The container crane operator is responsible for configuring and controlling the container trajectory, managing oscillations and skewness, and preventing collisions between the crane, vessel, and other cranes, thereby ensuring the safe and efficient execution of the operation.
2.2 Dynamic Model of a Container Crane
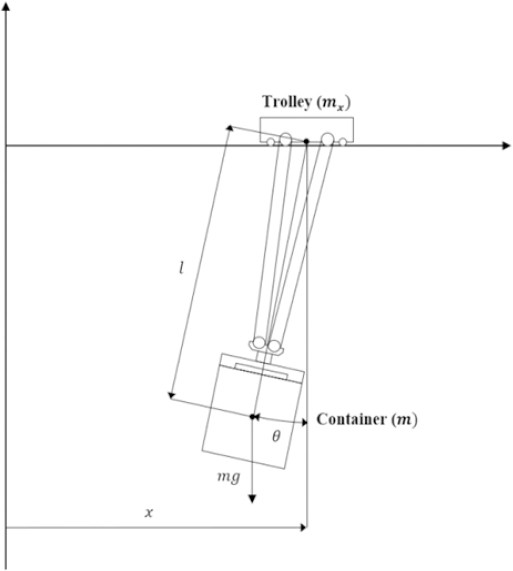
A dynamic model is employed to simulate container crane movements and transport container oscillations during vessel operations. This model focuses only on the movements of the trolley and hoist, which influence the container loading and unloading operations. The movement of the crane along the rails installed on the apron is not considered, and the oscillations of the container are assumed to occur only in the two-dimensional space formed by the movement of the trolley and vertical line.
Figure 2 shows the plane model of a container crane and its load (container), where x, l, θ are the horizontal position of the trolley, distance from the trolley to the container center, and swing angle, respectively. The load is considered as a point mass, and the mass and stiffness of the hoisting rope and the effects of wind disturbance are neglected. Subsequently, the equation of motion of the container crane system is obtained as follows [5][6]:
| (1) |
| (2) |
| (3) |
Equations (1), (2), and (3) represent the dynamics of the trolley, hoist, and container oscillations, respectively. Here, m, mx, and ml are the weights of the container, trolley, and hoist, respectively; fx is the force applied to the trolley in the x-direction and fl denotes the force applied to the hoist in the l-direction; dvx and dvl are the viscous damping coefficients associated with the motions along the x - and l-directions, respectively; g denotes the gravitational acceleration.
Based on these equations, the second-order nonlinear coupled differential equations for the dynamic energies of the trolley and hoist are defined as follows:
| (4) |
| (5) |
| (6) |
2.3 Literature Review
Lee [5] proposed a novel dynamic model for overhead cranes in a three-dimensional space based on previous studies on overhead cranes in a two-dimensional space. A two-degree-of-freedom swing angle was defined and used to derive a nonlinear dynamic model of the crane.
Lei et al. [7] designed a dynamic model to capture the threedimensional motion of a spreader based on the movements of the trolley and hoist of a container crane. Using Lagrange’s equations, they obtained a four-degrees-of-freedom dynamic model in the generalized coordinates of the spreader whose motion was analyzed with respect to the distance from the trolley to the container center and its acceleration.
Ismail et al. [3] proposed a sliding-mode control method that considered external interference during maritime container crane operations. LQR was used to determine the sliding surface, and a sliding-mode controller was designed to induce and maintain the state trajectory of the system on the sliding surface. Simulations demonstrated a reduction in the interference effects caused by strong waves and winds during maritime operations.
Lu et al. [4] focused on horizontal motion control and minimized the energy consumption of a double-pendulum crane system. A control problem was formulated based on the dynamic model of a crane system and an energy consumption function was defined. The control problem was discretized using quadratic programming, and the effectiveness of the proposed planning method was demonstrated using hardware experiments.
Zhang et al. [8] designed a PID-based control model for overhead crane position control and sway suppression under uncertain conditions. The parameters were adjusted according to LaSalle's invariance principle to ensure the Lyapunov stability. Experiments with actual cranes validated the robustness of the proposed approach against nonzero conditions and external interference.
Wang et al. [9] developed an intelligent optimization technology based on artificial neural networks for nonlinear overhead crane control. This method eliminated the requirement of an initial stabilization phase and conveniently executed adaptive control based on the developed update rules.
Zhang et al. [10] addressed the overhead crane control problem using an online reinforcement learning algorithm, called passivity-based online deterministic policy gradient. The neural network rules were updated to ensure system stability during learning by analyzing the energy of an overhead crane system.
Zhang et al. [11] addressed the problem of handling various cargo weights in overhead crane control using a deep reinforcement learning algorithm, called domain randomization memory-augmented beta proximal policy optimization (DR-MABPPO). The control problem was formalized as a latent Markov decision process that captured the cargo weight changes as latent variables. Domain randomization enabled the learning algorithm to explore a range of cargo weights. Introducing a beta distribution addressed the action-range issues, ensuring compliance with the physical constraints. Simulations confirmed that DR-MABPPO could learn a versatile control policy for handling cargo of various weights.
Previous research on crane dynamics, control models, and learning models primarily focused on minimizing the sway and energy consumption in overhead crane systems. However, there is a notable gap in the research on learning models for controlling the container trajectories. Therefore, this study designed a deep learning model to predict the trolley and hoist input force values. This enabled the movement of containers from initial positions to target locations, considering diverse cargo weights and trajectories.
3. Container Crane Control Learning Model
In this section, a deep learning-based container crane control learning model is designed to predict the input values of forces exerted on the trolley and hoist while moving the containers of varying weights from the given initial positions to target positions.
3.1 Deep Learning Model
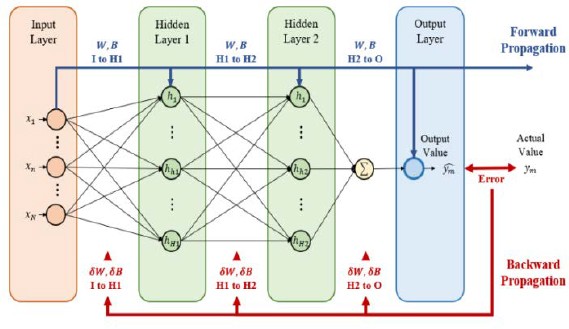
Deep learning or hierarchical learning is defined as a set of machine learning techniques based on artificial neural networks, which combine various nonlinear transformation methods to summarize the crucial content or functionalities within large datasets or complex information. The deep learning model in Figure 3 consists of input and output layers, with hidden layers placed between them. Each layer contains multiple nodes corresponding to an individual perceptron. Nodes within a specific layer are interconnected by those from the preceding and succeeding layers, and the weights represent the activation levels of these connections.
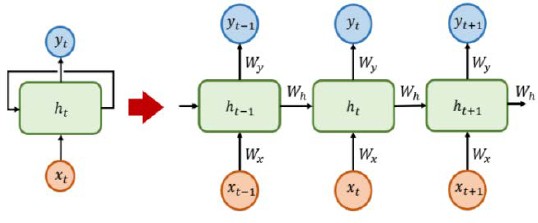
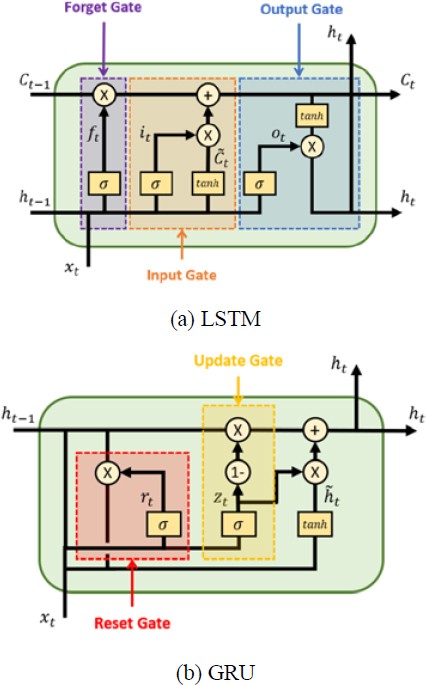
RNN is a type of artificial neural network that connects the cells within the hidden layer and sends their outputs to the output layer. These outputs serve as inputs for the next computation within the hidden layer. This recurrent internal structure, which retains the information related to previous time-step results, is useful for learning time-dependent or sequential data. Although RNNs can sequentially process input data of various lengths, they have the limitation of diminishing information transfer from the initial to final stages as the input data length increases. This issue, known as the problem of long-term dependencies in RNNs, leads to information loss as the learning progresses and sequence lengthens.
LSTM, which is a variant of the RNN proposed by Hochreiter et al. [12], was designed to address the long-term dependency problem. The basic operation of LSTM mirrors that of the conventional RNNs; however, the inclusion of the input, forget, and output gates within the cell enables it to resolve long-term memory loss problems. The input gate adjusts the input data, the forget gate determines the influence of the previous cell state using a sigmoid function ranging from 0 to 1, and the output gate modifies the input data by applying weighted values to each state. LSTM addresses the long-term dependency problem by allowing the cell to forget a certain amount of previous cell state data via the forget gate and update the current cell state by multiplying the previous output value and current input value based on the input gate output.
Cho et al. [13][14] proposed GRU, which is a simplified version of LSTM. In GRU, the update gate replaces the forget and input gates of LSTM. A reset gate is included to determine the part of the hidden layer cell, resulting from the previous time step, which is the output.
3.2 Model Architecture
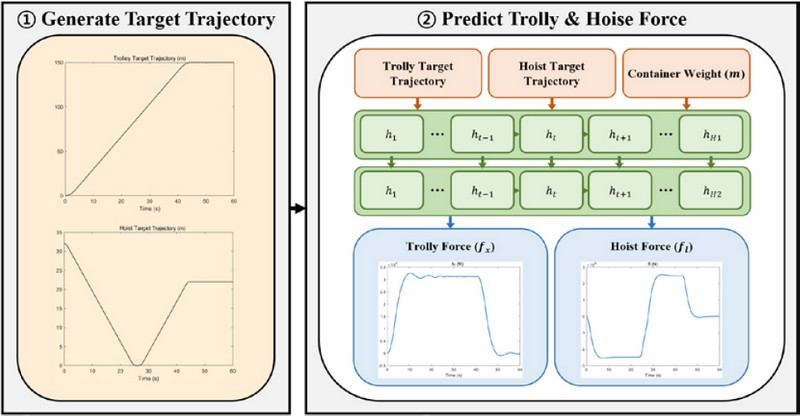
The designed deep learning-based container crane control learning model is structured into two phases, as shown in Figure 6.
The model generates the target movement path of the container from its initial position to its destination, that is, it calculates the time-dependent travel distances of the trolley and hoist when a container is moved, thereby minimizing the transportation time.
Subsequently, a deep learning model was designed to predict the trolley and hoist input force values based on the target movement path and container weight. The container crane control learning models were developed using the RNN, LSTM, and GRU models. Subsequently, the model demonstrating the best performance, confirmed using performance evaluation simulations, was identified.
3.3 Data Collection
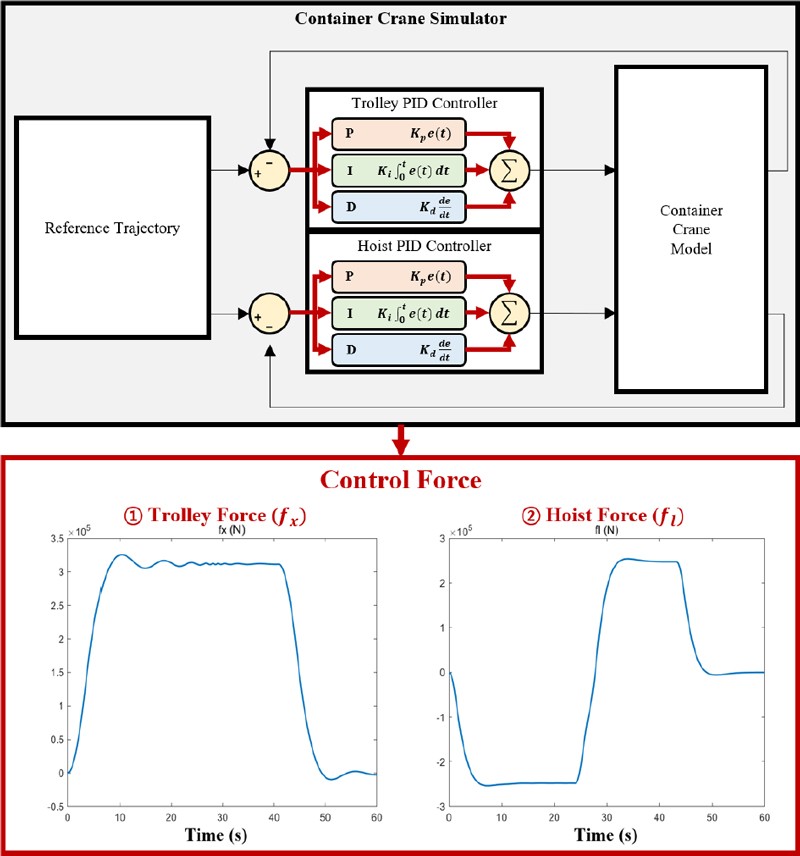
As shown in Figure 7, a container crane simulator was designed to emulate the control method employed by skilled operators to move containers to their target positions. The simulator incorporated the container crane dynamic model described previously and used a real-time PID controller to manipulate the trolley and hoist input force values, thereby replacing the role of the operator in moving the container.
Given the container weight, initial position, and target destination of the container, the simulator generated the input force values to facilitate the container movement based on the following procedure:
The current and target positions of the container were determined. The distance traveled by the trolley and hoist of the container within this range was measured. Based on operational specifications, including the acceleration, maximum speed, and deceleration of the trolley and hoist, the minimum time required to transport the container from the initial to the target position was calculated by setting the target trajectory of the container. The recorded positional information of the trolley and hoist for each time step was used as the setpoint variable for the PID control to determine their input force values.
During container-handling operations using a container crane, the container was assumed to be transported by lifting it from its initial position to a specified height to prevent collisions with other equipment, including containers, vessels, or cranes. Additionally, simultaneous movements of the trolley and hoist were assumed to expedite the handling operations, both attaining their respective maximum speeds concurrently.
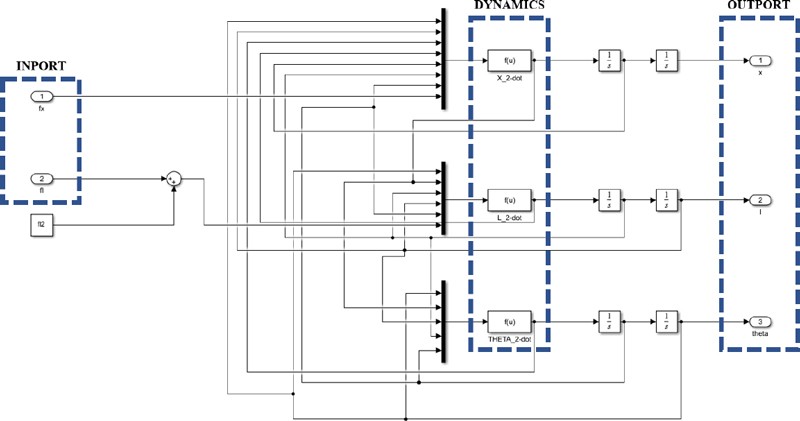
The output values of the inner dynamic model of the controlled object and container crane were measured based on the initial input values. Figure 8 shows the block diagram of the dynamic model of a container crane. The model read fx andfl from the input ports and calculated , and using the blocks X_2-dot, L_2-dot, and THETA_2-dot representing Equations (4)-(6), respectively. The trolley position, distance from the trolley to the container center, and swing angle of the container were obtained as outputs.
Subsequently, the process variables of the horizontal position x of the trolley and distance from the trolley to the container center l were compared with the target values, and the errors were calculated.
Using the error values between the process and setpoint variables, the control input values, i.e., fx and fl were calculated.
Subsequently, the container crane learning model was trained by generating and collecting data on the target trajectory of the container and the trolley and hoist input force values using the designed container crane simulator. The simulator was configured using dynamic model parameters based on the specifications of an actual container crane. Figure 9 shows that the initial and destination positions were randomly selected within a specified range, considering the size, outreach, and backreach of the container crane. The container weight was also selected randomly within a specified range based on the container weight information loaded onto the container vessels.
In this study, 10,530 cases of data were collected, encompassing different combinations of the initial position, destination, and container weight. These data were used to train the container crane control learning model.
Table 2 lists the specifications of the container crane control learning models based on the designed RNN, LSTM, and GRU. Each learning model comprised a three-layer structure. They were configured as many-to-many models, with the target trajectory of the trolley and hoist and container weight as input features, and the trolley and hoist input force values as output features. Additionally, a rectified linear unit was employed as the activation function for each hidden layer, and adaptive moment estimation served as the optimization function for the learning model.
The collected training data were split into training and validation datasets in the ratio of 80:20, and the training process utilized the mean square error (MSE) as the loss function. The number of epochs and learning rate were set to 5000 and 0.0001, respectively. However, to address the overfitting issues observed during training, the ModelCheckpoint feature was implemented to save the model at an epoch by minimizing the validation loss. These learning models were designed and trained using the Keras package within the TensorFlow library in Python.
4. Performance Evaluation
4.1 Simulation Environment
To evaluate the performances of the container crane control learning models, three vessel operation scenarios with varying initial positions, target positions, and container weights were defined, as shown in Table 3.
Scenario 1 represents the unloading operations, while Scenarios 2 and 3 represent the loading operations. Scenarios 1 and 2 focused on handling empty containers, whereas Scenario 3 involved handling full containers. For each scenario, the input force values of the trolley and hoist predicted by the RNN-, LSTM-, and GRU-based container crane control learning models were compared with the values calculated using the container crane simulator. The normalized root mean square error (NRMSE) was used to evaluate the prediction accuracy. NRMSE is a standardized metric derived by dividing the root mean squared error (RMSE) with the difference between the maximum and minimum values of the actual data. Similar to RMSE, a lower NRMSE value indicates higher predictive accuracy, which has been used in various studies on deep learning prediction models [15][16][17][18].
4.2 Simulation Results
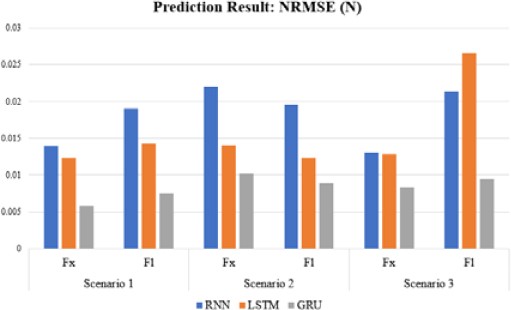
Based on simulation results, the average NRMSE values for the RNN, LSTM, and GRU models were 0.018164, 0.015381, and 0.008362, respectively. All three models demonstrated high prediction accuracy.
- ① In Scenario 1, the NRMSE value of the GRU model was the lowest at 0.006656, followed by those of the LSTM and RNN models at 0.013274 and 0.016513, respectively.
- ② In Scenario 2, the NRMSE value for the GRU model was the lowest at 0.009527, followed by those of the LSTM and RNN models at 0.013172 and 0.02076, respectively.
- ③ In Scenario 3, the NRMSE value of the GRU model was the lowest at 0.02076, followed by those of the RNN and LSTM models at 0.01722 and 0.019699, respectively.
The GRU model consistently outperformed in all the scenarios, confirming its effectiveness in predicting the input force values of the trolley and hoist to move the containers of various weights to the target position, as shown in Figure 10. Figure 11 compares the prediction results of the GRU model and simulator results for each scenario. GRU resolved the issue of long-term dependencies while maintaining a more compact structure, thereby accelerating training and prediction. This can be attributed to the streamlined architecture of the model, which is less sensitive to unnecessary details and facilitates the learning of more general patterns.
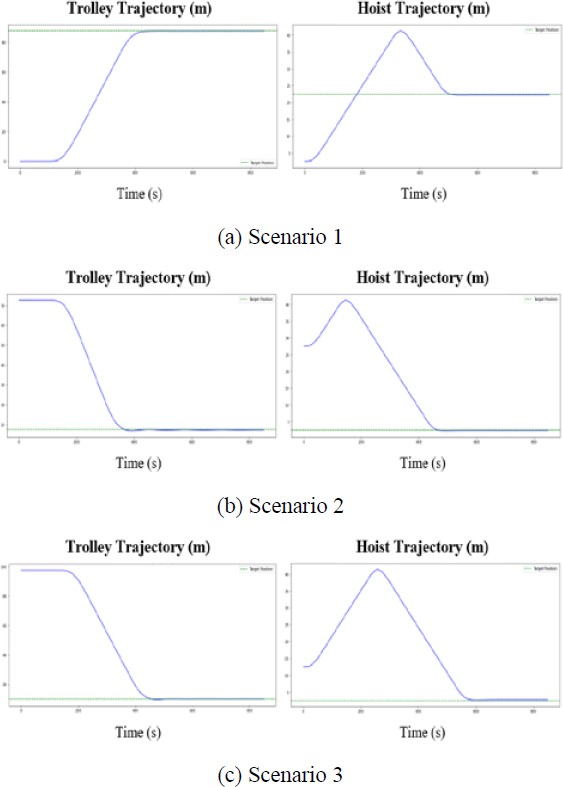
Furthermore, dynamic simulations were conducted for each scenario to assess the control performance of the GRU container crane control learning model. Particularly, the trolley and hoist input force values predicted by the GRU model were used as the input values for the container crane dynamic model, and it was verified whether the container moved to the intended target position.
Figure 12 shows the trolley and hoist trajectories in each scenario, where the input force values predicted by the GRU model were the dynamic model input values. As shown in Table 5, the dynamic simulation results of the GRU container crane control learning model indicated that the final x-axis position error of the container was within 0.1 m for Scenarios 1 and 3 and 0.2 m for Scenario 2. Additionally, the y-axis position error was within 0.1 m for Scenarios 1 and 2 and 0.2 m for Scenario 3.
5. Conclusions
This study designed a deep learning-based container crane control model to predict the forces required for moving containers of various weights to their destination positions when their initial and target locations are provided. Initially, a container crane simulator resembling the maneuvering techniques employed by skilled operators was devised. Subsequently, a simulator was used to obtain the dataset comprising 10,530 instances with different container weights, initial and target positions, and input force values of the trolley and hoist. The learned model used this dataset to establish the relationship between the container trajectory, weight, and trolley/hoist force inputs.
To evaluate the model performance, the force inputs were predicted in three distinct ship operation scenarios, each involving different initial container positions, target locations, and weights. The simulation results demonstrated that the designed deep learning-based container crane control learning model exhibited high prediction accuracy in various ship operation scenarios. Comparing the performances of the RNN, LSTM, and GRU models revealed that the GRU model consistently exhibited the highest prediction accuracy.
This research departs from previous studies that primarily focused on automating key functionalities within the container crane system, such as controlling container sway and skew. Instead, the emphasis is on designing a deep learning model for learning container movement path control.
Additionally, dynamic simulations were performed for the GRU model, confirming its ability to move the container to the intended position within an error of 0.2 m in all scenarios. However, real-world crane operations require fine-tuned position adjustments. Therefore, the application of the proposed model in actual container handling tasks necessitates research on improving the accuracy of predicting the trolley and hoist input force values.
The potential applications of this model to automated container crane control contribute to its significance. The model holds promise for developing programs aimed at training and educating container crane operators.
Acknowledgments
This research was supported by the 4th Educational Training Program for the Shipping, Port, and Logistics from the Ministry of Oceans and Fisheries.
Author Contributions
Conceptualization, H. S. Shin and H. S. Kim; Methodology, H. S. Shin; Software, H. S. Shin; Validation, Y. S. Ha; Formal Analysis, H. S. Shin & Y. S. Ha; Investigation, H. S. Shin & S. P. Lee; Resources, H. S. Shin; Data Curation, H. S. Shin & S. P. Lee; Writing-Original Draft Preparation, H. S. Shin & S. P. Lee; Writing- Review & Editing, Y. S. Ha; Visualization, H. S. Shin; Supervision, H. S. Kim; Project Administration, H. S. Kim; Funding Acquisition, H. S. Kim.
References
- Research and Markets, 2022.
-
X. Yu, X. Lin, and W. Lan, “Composite nonlinear feedback controller design for overhead crane servo systems”, Transactions of the Institute of Measurement and Control, vol. 36, no. 5, pp. 662-672, 2014.
[https://doi.org/10.1177/0142331213518578]

-
R. M. T. Raja Ismail, N. D. That, and Q. Ha, “Modeling and robust trajectory following for offshore crane systems,” Automation in Construction, vol. 59, pp. 179-187, 2015.
[https://doi.org/10.1016/j.autcon.2015.05.003]

-
B. Lu, Y. Fang, and N. Sun, “Modeling and nonlinear coordination control for an underactuated dual overhead crane system,” Automatica, vol. 91, pp. 244-255, 2018.
[https://doi.org/10.1016/j.automatica.2018.01.008]

-
H. -H. Lee, “Modeling and control of a three-dimensional overhead crane,” Journal of Dynamic Systems, Measurement, and Control, vol. 120, no. 4, pp. 471-476, 1998.
[https://doi.org/10.1115/1.2801488]

- H. -H. Lee and Y. Liang, “A robust anti-swing trajectory control of overhead cranes with high-speed load hoisting: Experimental study,” Proceedings of 2010 International Mechanical Engineering Congress and Exposition, vol. 8, Parts A and B, pp. 711-716, 2012.
-
L. Rong, M. Zhao, and J. H. Cui, “4-DOF dynamic model of the container crane spreader,” Applied Mechanics and Materials, vol. 511-512, pp. 985-989, 2014.
[https://doi.org/10.4028/www.scientific.net/AMM.511-512.985]

-
S. Zhang, X. He, H. Zhu, X. Li, and X. Liu, “PID Control of Overhead Cranes with Uncertainty”, Mechanical Systems and Signal Processing, vol. 178, pp.1-16, 2022.
[https://doi.org/10.1016/j.ymssp.2022.109274]

-
D. Wang, H. He, and D. Liu, “Intelligent optimal control with critic learning for a nonlinear overhead crane system,” IEEE Transactions on Industrial Informatics, vol. 14, no. 7, pp. 2932-2940, 2018.
[https://doi.org/10.1109/TII.2017.2771256]

-
H. Zhang, C. Zhao, and J. Ding, “Online reinforcement learning with passivity-based stabilizing term for real time overhead crane control without knowledge of the system model,” Control Engineering Practice, vol. 127, pp. 1-13, 2022.
[https://doi.org/10.1016/j.conengprac.2022.105302]

-
J. Zhang, C. Zhao, and J. Ding, “Deep reinforcement learning with domain randomization for overhead crane control with payload mass variations,” Control Engineering Practice, vol. 141, pp. 1-13, 2023.
[https://doi.org/10.1016/j.conengprac.2023.105689]

-
S. Hochreiter and J. Schmidhuber, “Long short-term memory,” Neural Computation, vol. 9, no. 8, pp. 1735-1780, 1997.
[https://doi.org/10.1162/neco.1997.9.8.1735]

- K. -H. Cho, B. Merrienboer, C. Gulcehre, D. Bahdanau, F. Bougares, H. Schwenk, and Y. Bengio, “Learning phrase representation using RNN encoder-decoder for statistical machine translation”, pp. 1724-1734, 2014.
- J. -Y. Chung, C. Gulcehre, K. -H. Cho, and Y. Bengio, “Empirical evaluation of gated recurrent neural networks on sequence modeling,” arXiv:1412.3555, , 2014.
-
J. -H. Kim, C. -G. Lee, J. -Y. Shon, K. -J. Choi, and Y. -H. Yoon, “Comparison of statistic methods for evaluating crop model performance,” Korean Journal of Agricultural and Forest Meteorology, vol. 14, no. 4, pp. 269-276, 2012 (in Korean).
[https://doi.org/10.5532/KJAFM.2012.14.4.269]

-
J. -P. Cho, I. W. Jung, C. -G. Kim, and T. -G. Kim, “One-month lead dam inflow forecast using climate indices based on tele-connection,” Journal of Korea Water Resources Association, vol. 49, no. 5, pp. 361-372, 2016 (in Korean).
[https://doi.org/10.3741/JKWRA.2016.49.5.361]

-
C. -H. Choi, K. -H. Park, H. -K. Park, M. -J. Lee, J. -S. Kim, and H. -S. Kim, “Development of heavy rain damage prediction function for public facility using machine learning,” Journal of the Korean Society of Hazard Mitigation, vol. 17, no. 6, pp. 443-450, 2017 (in Korean).
[https://doi.org/10.9798/KOSHAM.2017.17.6.443]

-
S. -W. Hwang, “Assessing the Performance of CMIP5 GCMs for various climatic elements and indicators over the southeast US,” Journal of Korea Water Resources Association, vol. 47, no. 11, pp. 1039-1050, 2014 (in Korean).
[https://doi.org/10.3741/JKWRA.2014.47.11.1039]

-
S. -H. Kang, S. -J. Lee, and Y. -Y Choo, “Development of a remote operation system for a quay crane simulator,” Journal of Institute of Control, Robotics and Systems, vol. 21, no. 4, pp. 385-390, 2015 (in Korean).
[https://doi.org/10.5302/J.ICROS.2015.14.0112]

-
D. -Y. Kim, B. -J. Jung, and D. -H. Jung, “High performance control of container crane using adaptive-fuzzy control,” Journal of the Korean Institute of Illuminating and Electrical Installation Engineers, vol. 23, no. 2, pp. 115-124, 2009 (in Korean).
[https://doi.org/10.5207/JIEIE.2009.23.2.115]

- Y. -B. Kim, D. -H. Moon, J. -H. Yang, and G. -H. Chae, “An anti-sway control system design based on simultaneous optimization design approach,” Journal of Ocean Engineering and Technology, vol. 19, no. 3, pp. 66-73, 2005 (in Korean).
-
Y. -H. Kim and S. -M. Jang, “Operation of container cranes using ℓ₁-optimal control,” Journal of Navigation and Port Research, vol. 29, no. 5, pp. 409-413, 2005 (in Korean).
[https://doi.org/10.5394/KINPR.2005.29.5.409]

-
W. -B. Baek, “A second order sliding mode control of container cranes with unknown payloads and sway rates,” Journal of Institute of Control, Robotics and Systems, vol. 21, no. 2, pp. 145-149, 2015 (in Korean).
[https://doi.org/10.5302/J.ICROS.2015.14.0092]

-
S. -H. Shin and Y. -K. Kim, “A study on container terminal layout and the productivity of container crane during ship turnaround time,” Journal of Korea Port Economic Association, vol. 39, no. 1, pp. 47-63, 2023 (in Korean).
[https://doi.org/10.38121/kpea.2023.3.39.1.47]

-
Y. Bengio, A. Courville, and P. Vincent, “Representation learning: A review and new perspectives,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 35, no. 8, pp. 1798-1828, 2013.
[https://doi.org/10.1109/TPAMI.2013.50]

-
A. Sherstinsky, “Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network,” Physica D: Nonlinear Phenomena, vol. 404, pp. 1-28, 2020.
[https://doi.org/10.1016/j.physd.2019.132306]

-
Y. Yu, X. Si, C. Hu, and J. Zhang, “A review of recurrent neural networks: LSTM cells and network architectures,” Neural Computation, vol. 31, no. 7, pp. 1235-1270, 2019.
[https://doi.org/10.1162/neco_a_01199]

- W. Zarenba, I. Sutskever, and O. Vinyals, “Recurrent neural network regularization,” arXiv:1409.2329, , 2014.