Two-dimensional horizontal motion of two floaters with internal flow using higher-order multi-modal method
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Previous studies have focused on the problem of sloshing, and coupling with body motion has only been conducted using a single-mode dominant method. Moreover, although the problem of secondary resonance induced by an internal fluid with sufficiently deep tank depths has been studied using the two-mode dominant method, sloshing below critical tank depths requires considerable research. This study investigated the two-dimensional horizontal motion of two rectangular boxes, including the internal flow. The hydrodynamic coefficients were calculated using the constant panel method, and the effect of the internal fluid was calculated using a multimodal method based on the Bateman-Luke variational principle. Consequently, the characteristics of the internal fluid motion were categorized based on the ratio of the internal fluid depth(h) to the tank length(l). For h/l values below the critical depth ratio (approximately 0.337 for a rectangular water tank), the single-mode dominant method was considered inappropriate for precisely describing the sloshing phenomenon. Therefore, the aim of this study was to develop higher-order multimodal methods. The numerical results were compared with previous experimental data. Furthermore, a parametric study of modal damping was conducted.
Keywords:
Sloshing; Two floating barges, Two-dimensional horizontal motion, Finite-depth liquid tank, Multi-modal method; Modal damping1. Introduction
Sloshing is a classic area of fluid dynamics that has been studied extensively. In the 2000s, as the demand for liquefied natural gas (LNG)-related ships and offshore structures rapidly increased, considerable research on the effects of sloshing loads on hull motion was conducted [1]-[3]. This is because, in contrast to traditional LNG carriers, loading and unloading operations are conducted at sea, and as the water level inside the tanks varies, the effects of sloshing have a significant impact on ship motion. In particular, for membrane-type LNG carrier vessels, the ship and tank widths had similar values. The effects of ship motion on sloshing have been closely studied because the natural periods of a ship's horizontal and sloshing modes are similar.
Regarding numerical methods, several in-house code development studies based on OpenFOAM and application studies using the StarCCM have been conducted [4]-[9]. They are based on the Navier-Stokes equations and have the disadvantage of requiring considerable computation time, although hardware has improved drastically in recent years. However, few studies have attempted to interpretatively solve this problem using this potential.
Faltinsen et al. analytically approached the sloshing problem by formulating a multimodal method using the Bateman–Luke minimum energy principle [10]-[11]. They studied single- and two-mode-dominant methods by varying the number of dominant sloshing modes [12]. However, these studies focused on the problem of sloshing, and coupling with body motion was only conducted using a single-mode-dominant method. Therefore, higher-order methods were not applied to the coupling problem, and were only applied to the internal flow. In addition, the problem of secondary resonance induced by an internal fluid with sufficiently deep tank depths has been studied by introducing a two-mode dominant method. However, sloshing below critical tank depths still requires considerable research.
The aim of this study was to establish a higher-order multimodal method for one-degree-of-freedom horizontal motion and apply it to a floating body-internal flow coupling analysis method. The developed method was applied to the problem of the effect of sloshing flow on the horizontal motion of two rigidly connected rectangular floating bodies [13]-[16]. The effect of varying the modal damping value on the results was also investigated, and the results were compared with existing experimental results.
The coefficients of the dynamic fluid forces were obtained by the boundary element method using the wave Green function [17]-[18], which was extended to a time-domain analysis using the convolution function [19]. The external force caused by the sloshing flow was modeled using a multimodal method [11]. Coupling analysis was performed by repeatedly delivering the displacement of the floating body and the sloshing force into each governing equation. Consequently, the time integration method was implemented using the fourth-order Runge-Kutta method. The calculated time-series results were then converted to a transfer function (motion driven by the external wave amplitude) in the frequency domain by extracting only the displacement of the motion from the steady state through the transition zone.
The remainder of this paper is organized as follows. In Section 2, we briefly summarize the mathematical formulations, including the external and internal flow models, higher-order multimodal method expansion, and coupling. Section 3 constitutes the numerical results obtained using established techniques, a comparison with previous experimental results, and the effects of adjusting the damping coefficients. The conclusions are presented in Section 4. Finally, the governing equations for each sloshing mode in the three-mode dominant method are provided in the Appendix.
2. Coupling between Floater and Sloshing
The sway motion in the time domain may be expressed as follows.
| (1) |
where M is the structural mass of the floating body, A22(∞) is the sway added mass at infinite frequency, is the wave viscous damping coefficient, h22(t) is the time-memory function obtained using the wave excitation damping coefficient, and , and are the wave excitation force, sloshing force, and friction, respectively, from the tank rail acting against the motion. Detailed explanations of these methods are provided elsewhere [10].
Here, the force due to sloshing was derived from the Bateman-Luke variational principle, which is based on the minimum principle of pressure variation. The governing equations for internal flow can be expressed using the following tensor equations [11]:
| (2) |
where,
| (3) |
| (4) |
| (5) |
where βi is the i-th generalized sloshing mode for calculating the sloshing force, δam is Kronecker Delta, σm is the sloshing natural frequency, ξm is the viscous damping coefficient for internal flow, and (t) is the external force owing to the sloshing flow. The coefficients (D1, D2, T0, T1) are determined by the water level and length inside the tank, and their relationship and derivation are described in detail in a previous study [11]. Further, η2 is the sway motion of the tank, l is the tank length, h is the tank water depth, and g is the gravitational acceleration.
In this study, a three-mode dominant method was developed based on the assumption that all three modes were dominant when using a multimodal method to describe the internal flow. Therefore, the number of dominant sloshing modes increases to three.
| (6) |
| (7) |
| (8) |
Equations (6) and (7) are the magnitudes of the sloshing modes in the single- and two-mode dominant methods established in a previous study, and Equation (8) is an assumption of the magnitudes developed in this study. Substituting Equation (8) into Equation (2) and removing the higher-order terms yields the governing equation. The final governing equation of the generalized sloshing modes for the internal flow, assuming three dominant sloshing modes, was introduced in a previous study [20] and is presented in the Appendix.
The viscous damping for a sloshing flow is based on Keulegan's model [21].
| (9) |
where LT and h are the transverse width and water depth of the internal tank, respectively; k and T are the wavenumber and wave period, respectively; and v is the kinematic viscosity coefficient of the inner fluid.
The force caused by the sloshing flow was obtained using the following equation, with the generalized sloshing modes calculated after solving Equation (2):
| (10) |
The sloshing force calculated using Equation (10) acted as the external force in Equation (1). The displacement and acceleration of the horizontal motion obtained by solving Equation (1) were substituted into Equation (10), and the ductile responses of the floating body and sloshing were calculated by iterating the two equations until the solutions converged.
3. Numerical Simulations
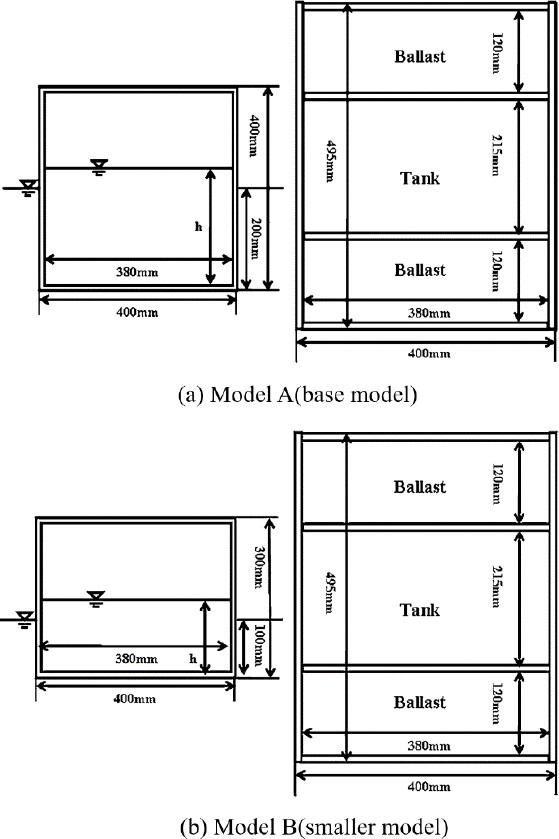
The numerical examples are based on the experimental results discussed in a previous study [13]. A previous study contained a detailed methodology and overall experimental procedure. The experimental setup is illustrated in Figure 1. The basic parameters of the two rectangular models and the water tank are listed in Table 1, and drawings of Models A and B are shown in Figure 2.
All other conditions were the same, with half the draft of Model A being that of Model B. The two models were rigidly constrained, and numerical analysis was performed for the case where the internal tank level was 50% for Model A and 40% for Model B. For the internal flow of Model A, we applied only the single-mode dominant method, whereas for Model B, we applied three numerical models: the single-, two-, and three-mode dominant methods, which were extended in this study.
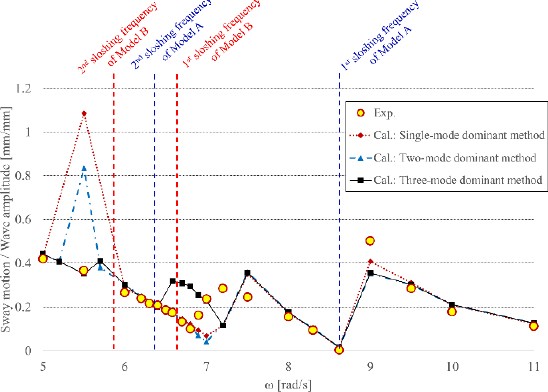
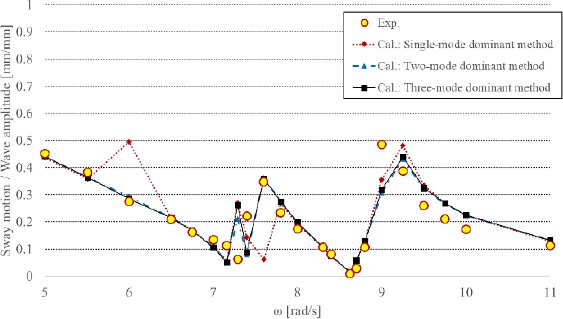
Figure 3 shows the transfer function for the horizontal motion of the models. The frequencies at which the secondary resonance occurred owing to each sloshing mode are presented in Table 2. From the second sloshing mode onwards, the frequencies were obtained using Equation (11) [11].
| (11) |
As shown in Figure 3, the effect of the internal flow of Model B based on the single- and two-mode dominant methods exhibited significant differences from the experiment at the frequency (ω = 5.5rad/s) where the secondary resonance of Model B occurred. However, when the three-mode-dominant method was applied, the numerical solution was similar to that of the experiment at this frequency.
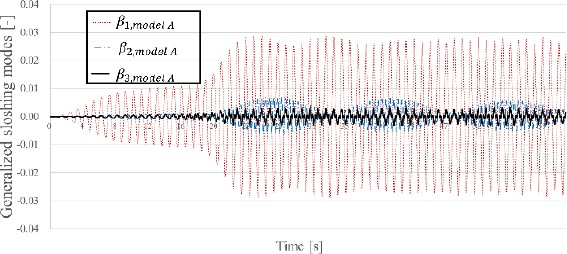
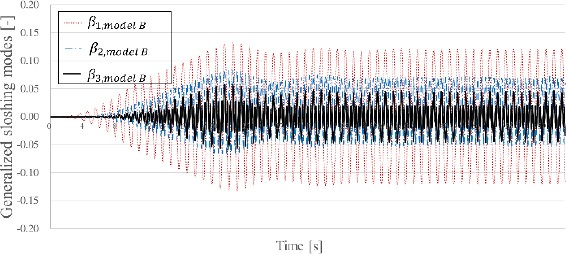
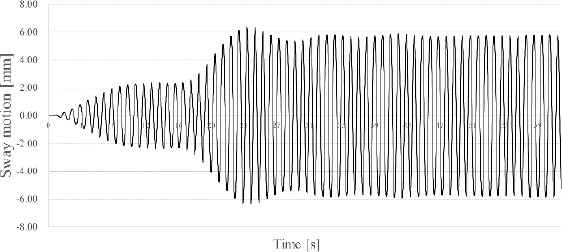
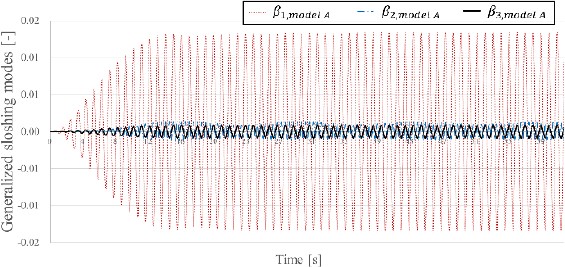
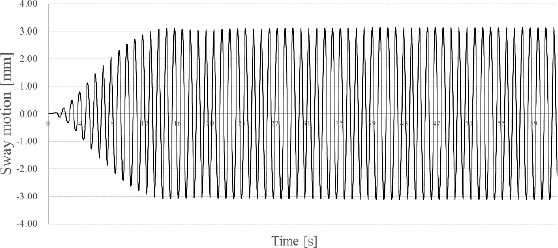
Moreover, near the first sloshing resonance of Model B (6.5-7.2 rad/s), the calculated values of all three analytical techniques differed from those of the experiment. To investigate this further, β1−3 for Model A, those of Model B, and the displacements of the horizontal motion of the model are shown in Figures 4, 5, and 6, respectively. These are the numerical results obtained after applying the three-mode dominant method at ω = 6.58rad/s.
In Figure 4, the β1 excess increased over time, indicating that this influence was dominant. However, in a previous study, the validity of the single-mode dominant method was verified when the model was filled to 50% [13]. Therefore, the need to improve the internal flow of Model B, modeled by the three-mode dominant method, was determined in this study. Because the sloshing modes of Models A and B were coupled, the sloshing modes of Model B may have affected the results of their counterparts in Model A.
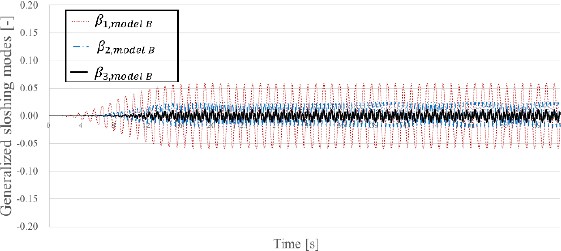
The Keulegan damping value was artificially increased to determine whether the sloshing modes in Model B were overestimated. For the internal flow of Model B, Figure 7 shows the results of increasing the modal damping value calculated using Equation (9) by a factor of five, and Figure 8 by a factor of 10.

Sway transfer function for the two models (50% filled Model A and 40% filled Model B) with modal damping, ξ = 5 × ξkeulegan

Sway transfer function for the two models(50% filled Model A and 40% filled Model B) with modal damping, ξ = 10 × ξkeulegan
As the modal damping value increases, the resultant excessive horizontal motion near the first sloshing resonance frequency of Model B gradually decreases. The resulting β1−3, displacements of the total horizontal motion for Models A and B corresponding to Figure 8, are also shown in Figures 9, 10, and 11.
In Comparison of Figure 10, Figure 5 reveals that the sloshing modes of Model B stabilized approximately 5 s earlier. Accordingly, Model A reached a steady state at approximately 12 s. Finally, the overall horizontal motion converged stably and the results of this motion were not significantly different from the experimental values.
Keulegan's modal damping coefficient model is essentially a boundary-layer formation model. Therefore, it is valid when the water level inside the model is sufficiently deep. However, at finite depths, its validity is limited by strong nonlinearity. Therefore, further studies on the modal damping should be conducted.
Finally, a numerical simulation was conducted for a slightly higher internal water level of 50% in Model B. The results are presented in Figure 12. The experimental values obtained using single- and two-mode-dominant methods were compared.
The numerical results obtained using the three-mode dominant method closely matched those obtained using the two-mode dominant method. When the water level in the internal tank exceeded a certain level, the values of the higher-order sloshing modes (β7−9) became approximately zero. Therefore, the three-mode-dominant method, which has a significantly more complex form, becomes indistinguishable from the two-mode-dominant method.
4. Conclusions
This study investigated the effects of internal flows at finite depths on floating-body behavior. A three-mode dominant method, which assumes up to three dominant sloshing modes in the internal flow, was derived and applied to the experiments in a previous study. The numerical results of single- and two-mode-dominant methods were also presented for comparison.
When Models A (50%) and B (40%) were filled, the problem of secondary resonance due to higher-order sloshing modes, which was a problem in the lower-order sloshing mode technique (single-dominant and two-mode dominant methods), was solved using the three-mode dominant method. However, in the first sloshing mode of Model B, the calculations did not accurately simulate the experiment. In this case, viscous damping can be adjusted to approximate the experimental value; however, this is not a fundamental solution.
For Models A (50%) and B (50%), the two-mode dominant method was consistent with the experimental results. In the three-mode dominant method, the values of the higher-order sloshing modes above 7th order converged to zero when the water level inside the small model exceeded a certain level.
Although the three-mode dominant method solves the problem of finite depth, further research on viscous damping models is required. In addition, beyond the valid range, it is almost the same as that of the low-order multimodal method. Therefore, further development is required for engineering applications.
Acknowledgments
This study was supported by grants from the National R&D Projects ‘Development of technologies to improve passenger ship efficiency based on renewable energy(20220091/PMS5480)’ and ‘Development of 1MW class Marine Test-bed for Adoptability Demonstration of Alternative Fuels(20210608/PMS5560)’ funded by the Ministry of Oceans and Fisheries, Korea, and a grant from the Endowment Project ‘Development of Basic Technologies in Eco-friendly Ship Fuel Reliability and Safety Evaluation(PES4740)’ funded by the Korea Research Institute of Ships and Ocean Engineering.
Author Contributions
Conceptualization, Y.H. Kim and H.S. Choi; Methodology, Y.H. Kim and H.S. Choi; Formulations, Y.H. Kim; Numerical simulations, Y.H. Kim; Graphs & Tables, Y.H. Kim; Writing—Original Draft Preparation, Y.H. Kim; Writing—Review & Editing, Y.H. Kim
References
-
G. Gaillarde, A. Ledoux, and M. Lynch, “Coupling between liquified gas and vessel’s motion for partially filled tanks: Effect on seakeeping,” RINA conference – Design & Operation of Gas carrier, London, UK, pp. 33-39, 2004.
[https://doi.org/10.3940/rina.gas.2004.06]

-
Y. H. Kim, B. W. Nam, D. W. Kim, and Y. S. Kim, “Study on coupling effects of ship motion and sloshing,” Ocean Engineering, vol. 34, no. 16, pp. 2176-2187, 2007.
[https://doi.org/10.1016/j.oceaneng.2007.03.008]

- B. K. Kim and Y. S. Shin, “Coupled seakeeping with liquid sloshing in ship tanks,” International Conference on Off-shore Mechanics and Arctic Engineering, The American Society of Mechanical Engineers, Estoril, Portugal, pp. 247-257, 2009.
-
H. J. Kim, Y. H. Choi, and Y. W. Lee, “Numerical analysis of 2-DoF motions of an ocean floater with sloshing effects,” Journal of the Korean Society of Marine Engineering, vol. 37, no. 6, pp. 617-622, 2013 (in Korean).
[https://doi.org/10.5916/jkosme.2013.37.6.617]

-
N. Parthasarathy, H. J. Kim, Y. H. Choi, and Y. W. Lee, “A numerical study on sloshing impact loads in prismatic tanks under forced horizontal motion,” Journal of the Korean Society of Marine Engineering, vol. 41, no. 2, pp. 150-155, 2017.
[https://doi.org/10.5916/jkosme.2017.41.2.150]

-
Z. -H. Wang, S. -C. Jiang, W. Bai, and J. -X. Li, “Liquid sloshing in a baffled rectangular tank under irregular excitations,” Ocean Engineering, vol. 278, 2023.
[https://doi.org/10.1016/j.oceaneng.2023.114472]

-
Y. I. Park, S. H. Park, J. H. Lee, J. E. Park, S. H. Park, S. E. Youn, and J. H. Kim, “Exploring the reduction of sloshing in a rectangular tank with a baffle using coupled Eulerian-Lagrangian analysis,” Journal of Advanced Marine Engineering and Technology, vol. 47, no. 2, pp. 70-77, 2023.
[https://doi.org/10.5916/jamet.2023.47.2.70]

-
M. -A. Xue, Y. He, X. Yuan, Z. Cao, and J. K. Odoom, “Numerical and experimental study on sloshing damping effects of the porous baffle,” Ocean Engineering, vol. 285, Part 1, 2023.
[https://doi.org/10.1016/j.oceaneng.2023.115363]

-
X. Jin, C. Dai, Z. Xia, M. -M. Liu, and M. Luo, “Characteristics of seismically-induced resonant sloshing waves and the effects of bed topography,” Ocean Engineering, vol. 279, 2023.
[https://doi.org/10.1016/j.oceaneng.2023.114521]

-
O. M. Faltinsen, O. F. Rognebakke, L. A. Lukovsky, and A. N. Timokha, “Multidimensional modal analysis of nonlinear sloshing in a rectangular tank with finite water depth,” Journal of Fluid Mechanics, vol. 407, pp. 201-234, 2000.
[https://doi.org/10.1017/S0022112099007569]

- O. M. Faltinsen, and A. N. Timokha, Sloshing, Cambridge University Press, NY, USA, 2009.
-
O. M. Faltinsen and A. N. Timokha, “An adaptive multi-modal approach to nonlinear sloshing in a rectangular tank,” Journal of Fluid Mechanics, vol. 432, pp. 167-200, 2001.
[https://doi.org/10.1017/S0022112000003311]

-
D. Y. Lee, G. N. Jo, Y. H. Kim, H. S. Choi, and O. M. Faltinsen, “The effect of sloshing on the sway motions of 2D rectangular cylinders in regular waves,” Journal of Marine Science and Technology, vol. 16, pp. 323-330, 2011.
[https://doi.org/10.1007/s00773-011-0130-5]

- Y. H. Kim, D. Y. Lee, H. G. Sung, and H. S. Choi, “A study on the effect of sloshing on the roll motion of a 2D rectangular box in regular waves,” Proceedings of the Twenty-Second International Offshore & Polar Engineering Conference, Rhodes, Greece, 2012.
- Y. H. Kim, H. G. Sung, S. K. Cho, and H. S. Choi, “An experimental study on the 2-DoF motion of side-by-side connected 2D rectangular cylinders with sloshing effect,” Proceedings of the Twenty-third International Offshore & Polar Engineering Conference, Anchorage, Alaska, USA, 2013.
-
Y. H. Kim, H. G. Sung, S. K. Cho, and H. S. Choi, “The sloshing effect on the roll motion and 2-DoF motions of a 2D rectangular cylinder,” Journal of the Society of Naval Architects of Korea, vol. 50, no. 2, pp. 69-78, 2013 (in Korean).
[https://doi.org/10.3744/SNAK.2013.50.2.69]

- Y. R. Choi and H. S. Choi, “Transient surge motion of a moored ship in random waves,” International Journal of Offshore and Polar Engineering, vol. 1, no. 3, pp. 239-241, 1991.
-
J. N. Newman, Marine Hydrodynamics, The MIT press, Cambridge, Massachusetts, USA, 1977.
[https://doi.org/10.7551/mitpress/4443.001.0001]

- W. E. Cummins, “The impulse response function and ship motions,” Symposium on Ship Theory, The Institute fur Shiffbau der Universitat, Hamburg, Germany, Report 1661, 1962. Available: http://hdl.handle.net/1721.3/49049, .
- H. S. Choi, “Problems on nonlinear free surface,” 2012 Workshop on Society of Marine and Offshore Fluid Research, Seoul National University, Seoul, Korea, August 2012.
-
G. H. Keulegan, “Energy dissipation, in standing waves in rectangular basins,” Journal of Fluid Mechanics, vol. 6, no. 1, pp. 33-50, 1959.
[https://doi.org/10.1017/S0022112059000489]

Appendix
Appendix
By substituting the sloshing modes assumed in Equation (8) into the governing Equation (2), and eliminating the higher order terms than ε1 for the internal flow, a total of nine equations for β1−9 can be achieved.
| (A.1) |
| (A.2) |
| (A.3) |
| (A.4) |
| (A.5) |
| (A.6) |
| (A.7) |
| (A.8) |
| (A.9) |
For (A.1) through (A.3), the first third generalized sloshing modes, β1−3 , can be obtained by iterating until the solution converges. Further, higher-order generalized sloshing modes can be obtained linearly. The coefficients (D1, D2, T0, T1) are determined by the water level and length inside the tank, and their relationship and derivation are described in detail in [11].