Predicting heat transfer performance in a complex heat exchanger for LNG FGSS development

Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this study, a reasonable design option for improving the thermal performance of a newly designed complex heat exchanger that can simultaneously heat LNG) and BOG) is analyzed and evaluated. The relative heat transfer rates are compared according to the changes in the steam supply method, and the flow characteristics, heat transfer rate, and internal pressure of the steam inside the shell of the complex heat exchanger are interpreted using computational fluid analysis. Without distribution plates, the heat transfer rate to LNG increases as the steam supply inlet in the complex heat exchanger increases. However, if distribution plates are present, then the heat transfer rate decreases. It is discovered that there is a significant difference in the heat transfer rates for BOG depending on the presence or absence of distribution plates, and the impact of the steam supply inlet is almost negligible. These results confirm that selecting an appropriate combination based on the design conditions is necessary for the optimal design of a complex heat exchanger.
Keywords:
Complex heat exchanger, Liquified natural gas (LNG), Boil off gas (BOG), Computational fluid dynamics (CFD)1. Introduction
Since the late 2010s, numerous greenhouse gas emission reduction strategies have been proposed to address the escalating issue of global warming, which has led to disaster damage due to climate change. The International Maritime Organization has established detailed regulations to reduce greenhouse gas emissions due to ships. However, it is difficult for large ships, which mostly use bunker C oil as fuel, to satisfy these regulations. Hence, there is an increasing demand for LNG-powered ships that can satisfy these regulations [1][2].
Liquefied natural gas (LNG) is a natural gas that is liquefied at high pressures and low temperatures. Given that natural gas has a much larger volume than its mass at room temperature, its transportation and storage in a gaseous state is highly inefficient [3][4][5]. Therefore, natural gas extracted via drilling is liquefied into LNG at high pressure and low temperature. Then, it is heated using a separate heat exchanger. LNG maintains its liquid state only at extremely low temperatures; therefore, it naturally evaporates within storage containers, producing Boil-Off Gas (BOG) [6]. Typically, BOG can be reliquefied to produce LNG or used for other applications.
Generally, the heat exchanger is a shell-and-tube heat exchanger (STHX). In a typical STHX, only one fluid can be heated or cooled. Therefore, to use simultaneously the LNG and BOG on a ship with a conventional STHX, two STHXs are required: one for vaporizing the LNG and the other for heating BOG. However, there are challenges in using this method on ships, where space is limited owing to the substantial volume occupied by STHXs.
When using an STHX to heat LNG on a ship, water- or glycol-based antifreeze is typically mixed with the heating fluid. Even when a glycol-based antifreeze is mixed with water, ice can form inside the STHX if the LNG temperature is below -160 ℃, impairing the performance of the STHX or damaging its internal structure.
The newly designed complex heat exchanger is a modified form of a conventional STHX designed to simultaneously heat two fluids (LNG and BOG) using a single heat exchanger. This is the first challenge that has not been addressed to date. Considering the requirements of the industrial field, high-temperature steam is chosen as the heating source to avoid icing problems that often occur in LNG vaporizers. Therefore, this development is significantly different from that of the conventional approach.
When steam is used as the heating fluid in a heat exchanger, it exchanges heat inside the shell and condenses into water, which then accumulates in the lower part of the shell. If baffles are used in a conventional STHX, the accumulated water can block the steam flow; therefore, in this type of heat exchanger, the baffle is not used for its original purpose but only to support the tube bundle, allowing the condensate to flow. The heat transfer depends on the steam supply rate, supply temperature, out-of-temperature conditions of BOG and LNG, and geometric shapes. Therefore, it is important to select an appropriate combination of steam supplies.
The aim of this study is to investigate the effect of different steam supply methods on the heat transfer performance and to derive reasonable design solutions.
2. Numerical analysis
2.1 Fluid analysis model
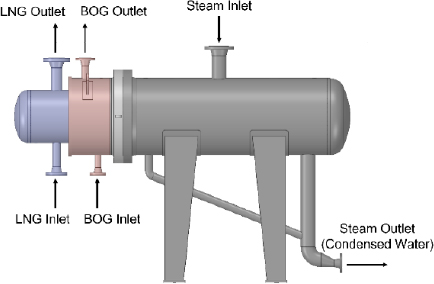
Figure 1 shows the basic shape of the complex heat exchanger analyzed in this study. The complex heat exchanger, which was initially designed using primary thermal calculations, contains 92 LNG tubes and eight BOG tubes. Table 1 lists the basic specifications of the complex heat exchanger.
At the inlet of the shell, steam is introduced at 6 barG and 168 ℃, while LNG and BOG are introduced at 16 barG and 4.5 barG, respectively, into the tubes at -163 ℃ and -140 ℃, respectively. The adiabatic condition is applied to the solid walls, except for the inner tubes, where heat exchange occurs. A pressure boundary condition is applied at the outlet.
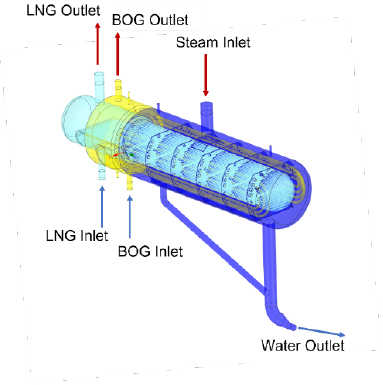
Figure 2 shows the fluid region of the heat exchanger shown in Figure 1, where the LNG tube bundle (light blue) is located at the center of the heat exchanger, and the BOG tubes (yellow) surround it on both sides. The steam enters from the upper inlet, exchanges heat with the LNG and BOG inside the shell, and is discharged from the lower outlet.
2.2 Governing equations and turbulence model
The fluid flow is considered steady, incompressible, and turbulent. The fluid properties used in the analysis are expressed as functions of temperature, assuming no change in pressure. The continuity equation, momentum equation, and energy equation are provided respectively below [7].
| (1) |
| (2) |
Wherein .
Here, τij is modeled using the viscous fluid model, whereas should be modeled as the turbulence model.
| (3) |
Furthermore, qi is modeled based on Fourier postulations, whereas and Φt should be modeled from the turbulence model. In this study, the standard k-ε turbulent model is used, which exhibits good convergence and stability for calculations compared to other models. For detailed turbulence quantities, please see References [8][9].
To test the grid independence of the analysis model, four mesh systems were generated with nodes ranging from approximately 6.7 million to 24.7 million, the results of the outlet temperatures for the four cases are compared in Figure 3.
As shown in Figure 3, the outlet temperatures of the 24.7 million-node analysis grid were within 0.2 °C of those of the 18.8 million-node analysis grid, with an error of less than 1% based on heat transfer rate. Therefore, the analysis in this study is conducted based on a 24.7 million-node grid, which is also used for other analyses under the same conditions.
Table 2 summarizes the cases analyzed in this study. To understand the effect of the steam supply method on the heat exchange, the effects of the presence(O) or absence(X) of a distribution plate for steam dispersion in front of the steam inlet and the number of steam supply inlets to distribute steam more evenly to the tubes were investigated. Cases 1-X in Table 2 indicate that there is only one steam inlet(1) and no distribution plates(X) in front of the steam inlet.
Table 2 presents a summary of the cases examined in this study. To understand the impact of the steam supply method on heat exchange, the effect of the presence (O) or absence (X) of a distribution plate on steam dispersion in front of the steam inlet is investigated. Furthermore, the effect of the number of steam supply inlets used to distribute steam more uniformly across the tubes is investigated. Case 1-X in Table 2 indicates that there is only one steam inlet(1) and no distribution plates(X) in front of the steam inlet.
3. Results and discussion
3.1 Effects of steam supply method
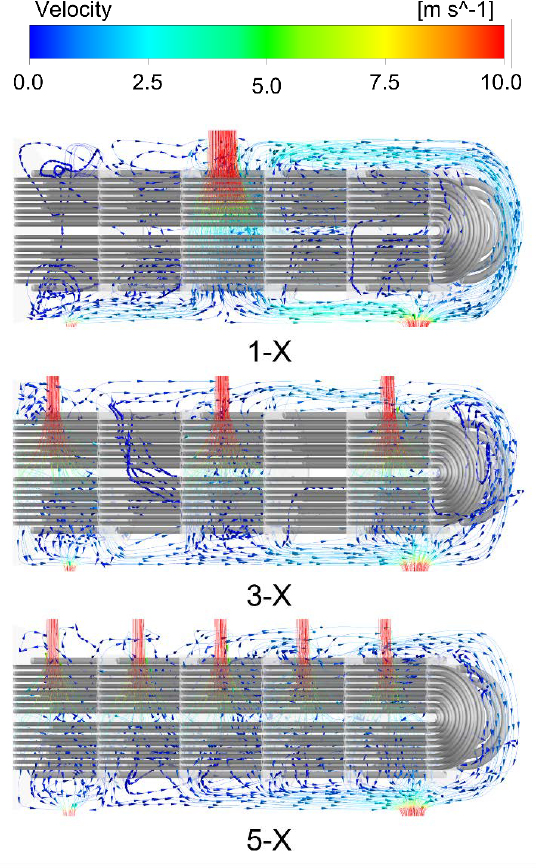
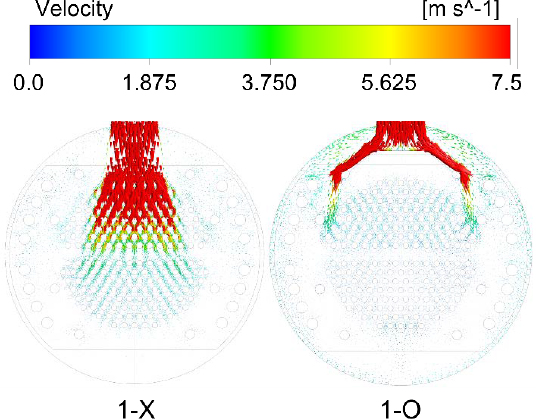
Figure 4 shows the flow analysis results for steam with and without a distribution plate in front of the inlet, when there is only one steam inlet. The streamlines are represented by lines randomly selected from 128 points on the inlet surface.
When checking the streamlines in Figure 4, the steam flow toward the tube is relatively evenly distributed when there is a distribution plate in front of the inlet (O) compared to when there is no distribution plate (X). When there is no distribution plate, the steam flow is mainly generated directly below the inlet and toward the right side.
This is due to the fact that there is a flow space between the U-shaped tube and shell on the right side, but the space between the tube bundle and shell on the left side is narrow, resulting in a relatively higher flow resistance. Hence, the streamline develops toward the right side. This flow ultimately affects heat transfer, and it is confirmed that the average outlet temperature of Steam Outlet 1-X is 59.37 ºC, while the average outlet temperature of Steam Outlet 1-O is 55.67 ºC. This shows that more heat is transferred through Steam Outlet 1-O than through 1-X, indicating that 1-O has a better overall heat transfer rate than 1-X.
Figure 5 shows the streamlines of the analysis results used to investigate the effect of the number of steam supply inlets. In this case, the inlet velocity was maintained constant, and the same amount of total heat supply was provided.
When checking the streamlines in Figure 5, it can be estimated that as the number of inlets increases, the area where the fluid with a relatively faster velocity passes through the tube and contacts the tube expands uniformly, resulting in more efficient heat transfer. The average outlet temperature of Steam Outlet 1-X in Figure 5 is 59.37 ℃, that of Steam Outlet 3-X is 49.33 ℃, and that of Steam Outlet 5-X is 44.19 ℃, showing that the overall heat transfer rate of steam increases as the number of steam inlets increases. Figure 6 shows the heat transfer rate supplied to the BOG for all the analysis cases, and Figure 7 shows the heat transfer rate supplied to the LNG.
In the case of the LNG, when there was no distribution plate, the amount of heat transferred to the LNG increased linearly as the number of steam inlets increased.
Although there was a significant difference in the heat transferred based on the presence or absence of a distribution plate in front of the steam inlet for BOG, there was almost no difference in the heat transferred based on the number of inlets. The difference in transferred heat, based on the presence or absence of a distribution plate, is shown in Figure 8. When there is a distribution plate in front of the steam inlet, the steam supplied late is deflected toward the BOG tube, whereas without the distribution plate, the steam is deflected toward the LNG tube.
Figure 9 shows the heat transfer rate released by the steam. When there is a distribution plate, the heat transfer rate decreases as the number of inlets increases, whereas when there is no distribution plate, the heat transfer rate released by steam increases as the number of inlets increases.
3.2 Steam pressure distribution of heat exchanger
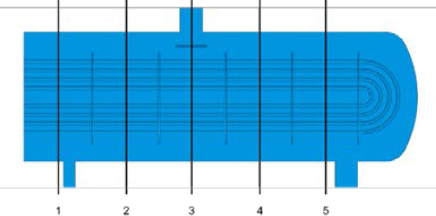
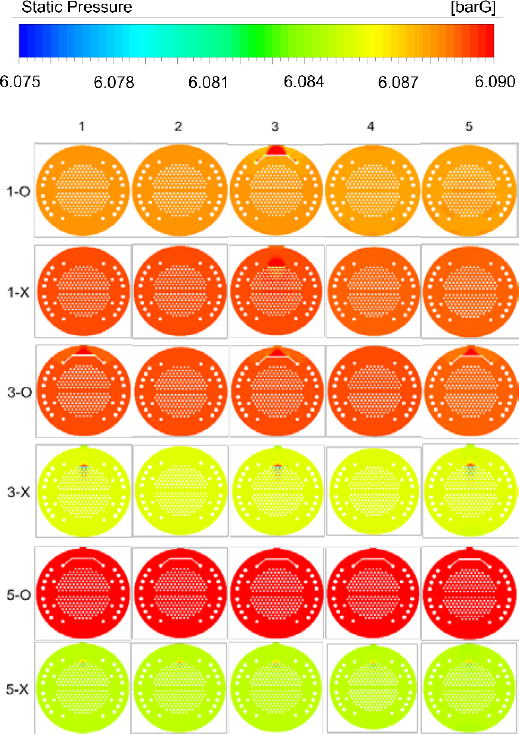
When steam flows inside the heat exchanger, pressure loss occurs because of friction with the tube bundle of the heat exchanger. Figure 10 shows the location of the cross section displaying the pressure distribution shown in Figure 11, which represents the pressure distribution inside the steam shell for each analysis case.
Regarding the pressure distribution, even in cases where the pressure change is the highest among all the cases, the difference is only 0.01 barG in absolute value when compared to the absolute pressure (6 barG) supplied to the steam inlet. Therefore, it can be confirmed that the pressure change owing to the change in the supply method to the shell is negligible.
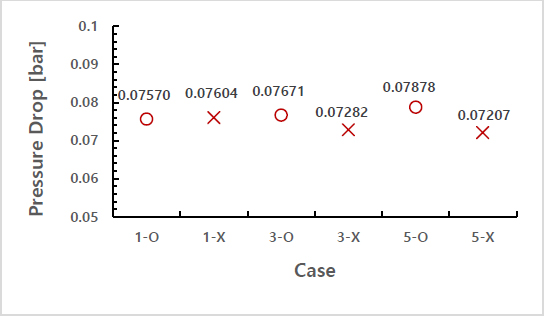
Figure 12 shows the pressure drop between the steam inlet and outlet. The largest pressure difference was 0.07878 barG, which was relatively small compared to the pressure supplied to the steam inlet, which was 6 barG. This indicates that the pressure drop was very small.
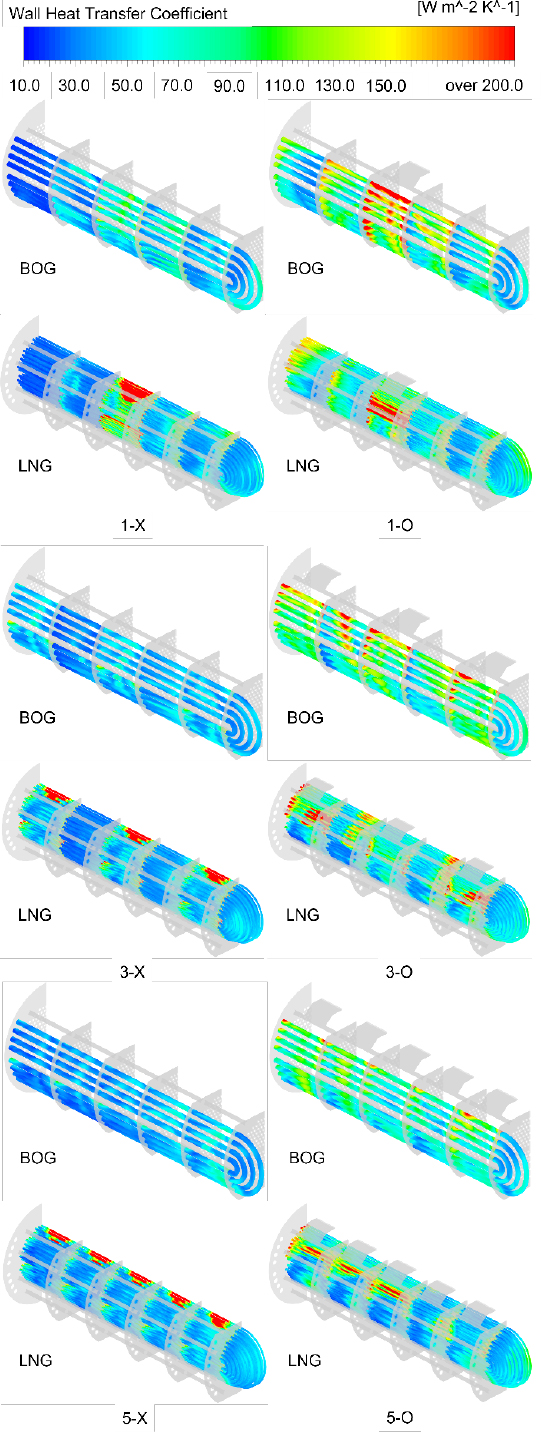
3.3 Heat transfer coefficient in the tube bundle
Figure 13 shows the heat-transfer coefficients of the surfaces of BOG and LNG tubes for each case. Referring to the streamline distributions in Figures 4 and 5, it can be confirmed that in the cases without a distribution plate in front of the steam inlet, steam was directly injected into the LNG tube bundle located at the center of the shell, resulting in a significant amount of heat transfer on the side of the LNG tubes. In the cases with a distribution plate, steam flowed through the distribution plate toward the BOG tube side, where the heat-transfer coefficient increased.
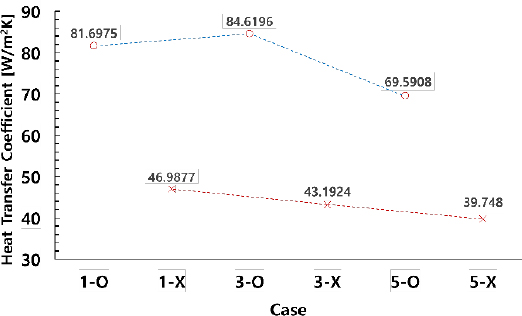
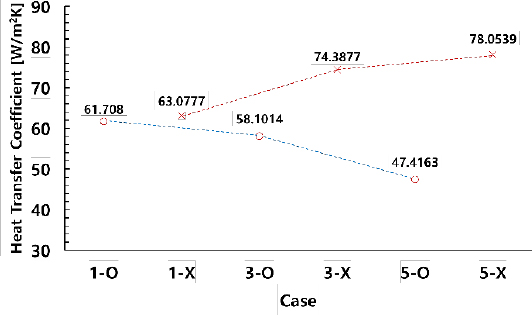
Figure 14 and shows the average heat transfer coefficients on the surfaces of BOG tubes, while Figure 15 shows the average heat transfer coefficient on the surface of LNG tubes. Figures 14 and 15 show the same trend as Figures 6 and 8 for the heat transfer amounts of BOG and LNG.
The purpose of the complex heat exchanger was to supply heat evenly to LNG and BOG. As shown in Figures 8 and 9, in the cases without a distribution plate, steam is concentrated toward the LNG tube bundle inside the shell, resulting in an increase in the heat transfer amount. In cases with a distribution plate, steam flowed toward the BOG tube side more strongly than toward the LNG tube side, leading to a decrease in heat transfer. Therefore, the selection of an appropriate combination is dependent on the supply rate, supply temperature, and outlet temperature conditions of BOG and LNG. Additionally, the impact of the shape of the distribution plate and selection of the positions of BOG and LNG tubes should be reviewed in the near future.
4. Conclusions
In this study, computational fluid dynamics (CFD) was used to analyze a newly proposed complex heat exchanger and compare the heat transfer rates and steam pressure drops under different conditions. Based on these results, the following conclusions were drawn:
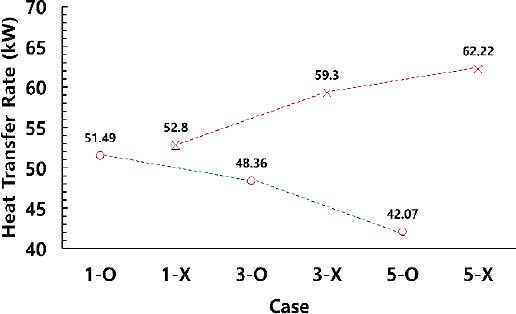
- 1. In the absence of a distribution plate, an increase in the number of steam inlet ports leads to an increase in the heat-transfer rate to the LNG side from 52.8 kW to 62.2 kW. However, if a distribution plate is present, the flow deflection reduces the heat transfer rate from 51.5 kW to 42.1 kW.
- 2. For the BOG, the presence or absence of a distribution plate has a significant impact on the heat transfer rate, whereas the number of steam inlet ports has little effect. When using a distribution plate, regardless of the number of distribution plates, the heat transfer rate increased by approximately 78% when compared with that in the absence of a distribution plate.
Therefore, it was confirmed that the selection of an appropriate combination of steam supply methods based on the design conditions is necessary for an optimal complex heat exchanger design.
Acknowledgments
The paper is a revised version of a paper entitled “Fluid Flow of Complex Heat Exchanger for LNG Fuel Gas Supply System” presented at KOSME spring conference 2022, Jeju, Korea. And this study was supported by Small and Medium Enterprise Technology Development Program (Export-Oriented) funded by the Ministry of SMEs and Startups. (S3060038).
Author Contributions
Conceptualization, J. W. Heo and Y. W. Lee; Methodology, J. W. Heo, Y. H. Choi, S. H. Kim and D. I. Yu; Software, W. Heo, Y. H. Choi; Validation, J. W. Heo and Y. W. Lee; Formal Analysis, J. W. Heo and Y. H. Choi; Investigation, J. W. Heo ; Resources, Y. W. Lee ; Data Curation, J. W. Heo, S. H. Lee and H. Y. Choi; Writing—Original Draft Preparation, J. W. Heo ; Writing—Review & Editing, Y. H. Choi, D. I. Yu and Y. W. Lee; Visualization, J. W. Heo; Supervision, Y. W. Lee; Project Administration, Y. W. Lee; Funding Acquisition, Y. W. Lee and S. H. Kim.
References
- UNFCCC, Conference of the Parties (COP), Adoption of the Paris Agreement, December 12, 2015.
- Korea Export-Import Bank, Global LNG Industry and LNG Carrier Trends and Forecasts, 2022.
- Y. M. Yang and S. G. Lee “R&D plan of natural gas liquefaction plant technologies,” Proceedings of KIGAS spring conference, 2009.
-
M. Nakaiwa et al., “Evaluation of an energy supply system with air separation,” Energy Conversion and Management, vol. 37, no. 3, pp. 295-301, 1996.
[https://doi.org/10.1016/0196-8904(95)00787-3]

- H. Tuo, Y. Li, and H. Tan, “Combined cycle of air separation and natural gas liquefaction,”Huagong Xuebao/Journal of Chemical Industry and Engineering, vol. 59, no. 10, pp. 2498-2504, 2008.
- Y. S. Baek et al., “Study on the improvement of BOG recondensation process at LNG receving terminal." Journal of the Korean Institute of Gas, vol. 5, no. 3, pp. 23-28, 2001 (in Korean).
- C. J. Chen, Fundamentals of turbulence modelling, Crc Press, 1997.
- H. K. Versteeg and W. Malalasekera, An Introduction to Computational Fluid Dynamics: The Finite Volume Method, Pearson Education, 2007.
- ©ANSYS, Inc. ANSYS CFX Theory Guide. 2022.