[ICACE2022] Prediction of container throughout of Qingdao port using optimized echo state network and improved particle swarm optimization
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The container throughput in a container logistics system is an important technical index, irrespective of the method used to manage and forecast the port throughput. The Qingdao port, one of the most important ports in North China, has the advantage of being located in the "One belt One Road" position. At present, the forecasting method for the container transportation throughput of Qingdao port still needs to be optimized, and a model that can predict its development trend needs to be constructed. Echo state networks (ESN) have been widely used in time-series prediction owing to their simple structure and fast convergence speed. To solve the problem of the applicability of the random weight matrix generated in the ESN to a specific time series, this study proposes an improved particle swarm optimization (PSO) algorithm to optimize partial random weights in the ESN. Compared to the standard particle swarm optimization algorithm, the inertia weight and learning factor were adjusted to improve the optimization performance of the algorithm. Furthermore, by comparing the historical data with the predicted values, the prediction accuracy of the model was found to be over 98%. The container throughput of Qingdao port from 2022 to 2024 was predicted, which showed that the container throughput of Qingdao Port will maintain a rapid and stable growth trend.
Keywords:
Port container throughput, Echo state network, Particle swarm optimization algorithm, Wavelet transform, Qingdao port1. Introduction
Container transportation is a new mode of transportation that is safe, highly efficient, quality assuring, fast, and economical. In the past decades, container transportation has developed rapidly worldwide and has become one of the primary means of international cargo transportation. The trend of global economic integration shows that container transportation has been involved in the core interests of enterprises, as well as the economic lifeline of countries. This has far-reaching strategic significance in container transportation. Qingdao Port, China’s second largest port with a foreign trade of 100 million tons, is an international trade port and transit hub located on the shore of Jiaozhou Bay on the Shandong Peninsula bordering the Yellow Sea and the west coast of the Pacific Ocean.
Qingdao Port is the third largest container port in China after Shanghai and Shenzhen, and the main export port for coal and crude oil from the Shengli Oilfield in the Jinzhong area. It has the largest container, crude oil, and iron mine terminals in China. Qingdao Port has become one of the fastest-growing ports of container transportation in Northeast Asia and the largest port of international container transfer in Northern China.
The efficiency and international competitiveness of Qingdao Port's maritime transportation can be improved by carrying out reasonable and reliable port throughput forecasts, rationally deploying port resources according to the forecast results, and making the port's navigable capacity and investment in basic facilities consistent. Simultaneously, exploring the development trend of port throughput and accurately predicting the port throughput can effectively avoid the idle capacity of infrastructure and the wastage of resources, and help create a strategic plan for the development of the country's shipping industry as a whole, which is important for improving the layout of port infrastructure and the operations. Therefore, efficiency is crucial.
Time series prediction is used to predict the future according to the development process, direction, and trend of historical data by analyzing time series [1]. Time series prediction has been widely used in various fields, such as gene expression profiles in biology, stock prices in finance, urban traffic flow in society, wind energy assessment in industry, and climate temperature change prediction [2]. However, actual time series often show complex characteristics, such as non-stationary, random, high-dimensional, nonlinear, and non-periodic, and hence, the prediction research of time series still faces great challenges [3]. Therefore, this study analyzes and predicts the container throughput based on wavelet transform and proposes an improved particle swarm optimization algorithm to predict the time series of the echo state network. Furthermore, by combining the characteristics of Qingdao Port and the predicted result of container throughput, we propose a development plan for Qingdao Port container transportation.
Linear and nonlinear methods are used to predict time series data. Linear methods mainly include autoregressive moving averages [4] and autoregressive comprehensive moving averages [5][6]. These methods are suitable for predicting time series with long durations and relatively slow changes. Nonlinear methods mainly include the least squares support vector machine [7] and artificial neural networks. With the increasing scale and complexity of networks, nonlinear methods can deal with nonstationary, stochastic, high-dimensional, nonlinear, and nonperiodic problems of time series. Although nonlinear methods can effectively deal with complex time series, they have some limitations. A forward neural network has the problems of complex training algorithms, difficulty in determining the network structure, and large amounts of computation. An Echo State Network (ESN) is a new recursive neural network with good nonlinear approximation ability and can deal with nonlinear prediction problems well. Wavelet analysis is an effective method for dealing with nonstationary time series. Through wavelet decomposition, complex data in a time series can be decomposed into an approximately unrelated time series [8].
Particle swarm optimization (PSO), a meta-heuristic algorithm, has been widely used in neural network structure optimization, electric power, industry, and other fields owing to its simplicity, ease of implementation, and strong searchability. In [9], the author used the standard particle swarm optimization algorithm to optimize random weights in the echo state network and improve the prediction performance of the network.
The ESN network, a new type of recursive neural network, functions as short-term memory because the hidden layer of its reservoir, referred to as DR, comprises several sparsely connected neurons, which effectively solves the training difficulties of traditional recursive neural networks in large-scale applications. They are often used to model complex nonlinear systems. An ESN network typically uses a linear regression algorithm to solve the output weight. In the actual application process, an illconditioned solution can be easily generated, and the output weight of a large value affects the performance of the network prediction.
This study adopted the PSO algorithm to optimize the ESN network, combined with wavelet decomposition to eliminate high-frequency signals. Qingdao Port was used as an example to analyze and forecast the research. In this study, the input indicators of port throughput prediction are preprocessed by multimode fusion and integration, and the characteristics of the ESN network are utilized to construct an intelligent prediction model scientifically and effectively to accurately predict the typical port throughput. Furthermore, it provides solid technical support for port construction and emergency decision efficiency.
2. Materials and methods
2.1 Wavelet Transform
Wavelet Transform is a new method of transform analysis, its inheritance, and the development of the localization of the short-time Fourier Transform (STFT); simultaneously, to overcome the shortcoming of the latter window size that does not change with frequency, it can provide a change with the frequency of the time-frequency window. Therefore, it is considered an ideal signal time-frequency analysis and processing tool.
Wavelet Transform gradually refines the signal (function) at multiple scales through telescopic and translational operations, and finally achieves time subdivision at high frequency and frequency subdivision at low frequency by automatically adapting to the requirements of time frequency signal analysis and focusing on any details of the signal.
It is a mathematical tool that is based on signal analysis and has been proven efficient in various fields of application, such as image processing, data compression, and disaster prediction. The basic concept of wavelet analysis is to select a mother wavelength or proper wavelet and perform an analysis using its translated and dilated versions [10]. There are two categories of wavelet transforms: Continuous Wavelet Transforms (CWT) and Discrete Wavelet Transforms (DWT) [11][12]. The continuous wavelet transform W(a,b) of the signal f(t) with respect to a wavelet φ(t) is given as:
| (1) |
where φ(t) is the mother wavelet. The value of the wavelet transforms W(a,b) is called the wavelet coefficient, where a and b are real numbers known as the time scale or dilation variable and time shift or translation variable, respectively, which denote how many components of the wavelet at dilation a are included in the original signal at translation b.
The normalizing factor ensures that the energy remains the same for all a and b. Considering a closed subspace sequencej ∈ Z on L2(R), according to the multi-resolution theory, the space VO can be decomposed into
| (2) |
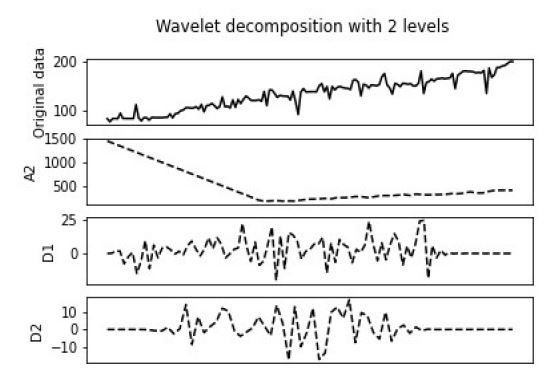
Figure 1 shows a schematic of the frequency space of wavelet decomposition based on multiresolution analysis, wherein the original frequency space is decomposed into a series of high-frequency subspaces reflecting details Di (i = 1,2, . . . , j) and a low-frequency subspace Aj that reflects the general picture. Here, Aj is a low-pass filter that can filter out the high-frequency part of the input signal and output the low-frequency part, and Di is a high-pass filter that filters out the low-frequency part and outputs the high-frequency part. The frequency domain of the wavelet function has bandpass characteristics, called a bandpass filter, whereas the scale function has low-pass characteristics in the frequency domain, called a low-pass filter [13].
2.2 Optimized echo state network by particle swarm optimization
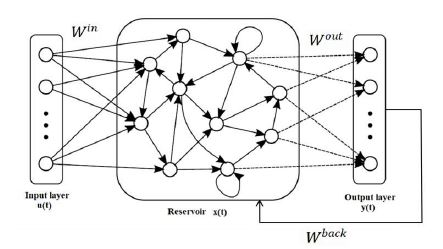
Jaeger and Haas (2001) proposed an ESN, a simple three-layer recursive neural network comprising an input, reserve pool, and output layers. U(t), x(t), and y(t) represent the input unit, state of neurons in the reserve pool, and the output unit at time t, respectively. Win , W , Wout, and Wback represent the connection weight matrix between the input layer and reserve pool, neurons in the reserve pool, input layer and output layer, reserve pool, the output layer, and the reserve pool, respectively. When Wback exists, the ESN can perform a multistep prediction; else, it can only perform a one-step prediction. In the ESN, the connection weights of the input layer to the reserve pool, the interior of the reserve pool, and the output layer to the reserve pool are randomly initialized and remain unchanged during training. Therefore, the ESN only needs to train the connection weights from the reserve pool to the output layer. The large-scale reserve pool replaces the fully connected hidden layer and enhances the modeling ability of the complex time series. Training only the connection weights between the reserve pool and the output layer can avoid the slow convergence speed of traditional neural networks based on the gradient descent principle, and may fall into the problem of local optimization when searching for the optimal solution. Figure 2 shows the structure of the basic ESN model. As shown in Figure 2, the layers are connected via different weight matrices [14][15]:
In the ESN, when signal U (t + 1) is input to the network, the update rules of the neuron status and network output in the reserve pool are given as:
| (3) |
| (4) |
where f and fout are the activation functions of the reserve pool and output unit, respectively; f is the hyperbolic tangent function tanh, and fout is the identity function.
When fout is the identity function, the model output y(t) can be expressed as:
| (5) |
During model training, we want to achieve a Wout that minimizes the error between the model's output Y (t) and the target value , that is, we solve the following optimization problem:
| (6) |
where k is the number of training samples.
PSO was proposed in 1995 by Kennedy, an American psychologist, and Eberhart, an electrical engineer, inspired by the foraging behavior of birds. PSO is a global random optimization algorithm based on swarm intelligence. It imitates the foraging behavior of birds, compares the search space of the problem with the flight space of birds, and abstracts each bird into a particle to represent a candidate solution to the problem. The optimal solution is equivalent to the food to be sought. The algorithm provides each particle with a position and speed, and each particle updates its own position by updating its speed. Through iterative search, the population can constantly find better particle positions to obtain a better solution to the optimization problem [16][17].
The principle of the PSO algorithm is as follows: n flying particles are in the solution space of dimension D, and the state of each flying particle can be described based on the position vector and flight velocity vector. Suppose vector Xi = (xi1, xi2, . . . xid) is the current position of flying particle I and vector Vi = (vi1, vi2, . . . vid) is the current flight speed of flying particle i , where 1 ≤ I ≤ n, 1 ≤ d ≤ D. The fitness function is defined, the fitness value of each flying particle is calculated, and the current optimal position Pi = (pi1, pi2, . . . pid) of the flying particle is selected according to the fitness value. Simultaneously, information sharing is carried out to screen out the current optimal location of the whole population, Pg = (pg1, pg2, . . . pgd) . When the algorithm starts to run, the position and speed of the flying particles are initially set, and the following formula is used to update their status of flying particles:
| (7) |
| (8) |
where constant W is the inertia weight, which significantly influences the global and local search abilities of the algorithm. Constants C1 and C2 are the cognitive and social factors, respectively, which represent the cognition of the particle to itself and the whole group, respectively. R1 and R2 are random numbers between [0,1].
In the learning process of the ESN, only the connection weights between the reserve and output layers are adjusted, whereas other connection weights remain unchanged after being assigned randomly. If these randomly assigned connection weights are not appropriately set, the prediction performance of the ESN can be directly affected. Therefore, the standard particle swarm optimization algorithm is used to optimize some random weights in the ESN to improve its prediction performance [18][19].
The training process of the ESN neural network determines the output weight matrix W of the system based on the given training samples. After the network structure of the ESN is randomly initialized, the training process of the ESN can be divided into two stages: sampling and weight training.
2.2.3.1 Phase of sampling
The network was initialized in the sampling stage. In general, the initial state of the network is selected as zero, that is x(0) = 0. The training sample (s(n), n = 1,2. . . , P) enters the dynamic reserve pool after the input connection weight Win.
2.2.3.2 Weight training stage
In this study, the PSO algorithm was used to train the ESN network output weight. The particle position in the PSO algorithm corresponded to the output connection weight of the neural network, and the adaptation function of the PSO algorithm adopted the output error function of the neural network, which constituted the weight training of the neural network with fewer sample data, that is, the training output weight W . The output connection weight-learning problem was transformed into an optimization problem.
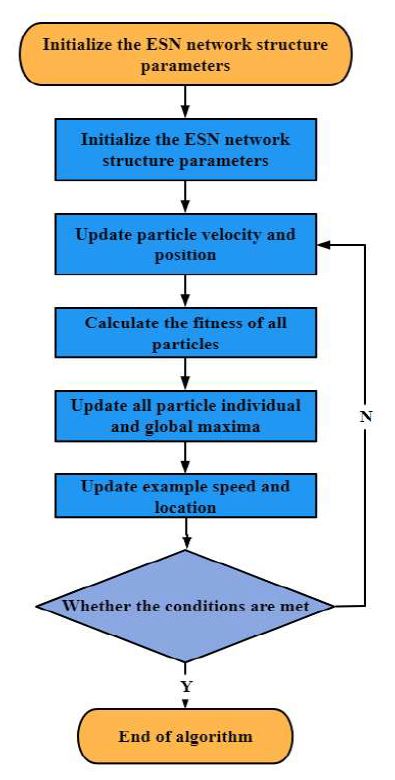
First, the ESN network parameters were initialized, and Win, W, Wout, and Wback were randomly generated. The population size of the particle swarm and maximum iteration algebra of the particle swarm were set. Each example in the particle swarm was described by the position vector P and velocity vector v. The particle position p directly encoded the possible solution to the problem; that is, all values of p represented a possible solution to the output weight W. A flowchart of the PSO-ESN algorithm is shown in Figure 3.
The ESN training process based on PSO optimization is as follows:
- Step 1: Initialize the ESN network structure, set the number of neurons in the input, hidden, and output layers of the network, and conduct standardized processing for the given training dataset.
- Step 2: The Velocity v and position P of each particle in the randomly initialized particle swarm in the n-dimensional search space.
- Step 3: Evaluate the fitness of each particle according to the mean square error function. If the current particle fitness < Pid , Pid= current particle fitness; else, the Pid remains unchanged. If the current particle fitness < Pgd, Pgd = current particle fitness value; else, Pgd remains unchanged.
- Step 4: Update the velocity vector v and position vector P of each particle according to Eqs. (7) and (8).
- Step 5: Repeat Steps 3 and 4 to determine whether the iteration termination conditions are met; if yes, terminate the program and output Pid as the initial output weight of the network to complete the initial weight training.
3. Simulation results
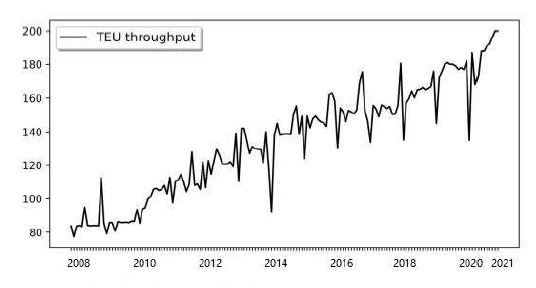
Qingdao port has superior geographical conditions, a vast hinterland, a developed economy, a first-class collection and distribution network, large-scale container transport, and sustainable development, which highlights the obvious comparative advantages of building an international shipping center in North China. The container throughput of Qingdao Port continues to increase rapidly. Figure 4 shows the container throughput data for Qingdao Port from 2008 to 2021 (units:10,000 TEU).
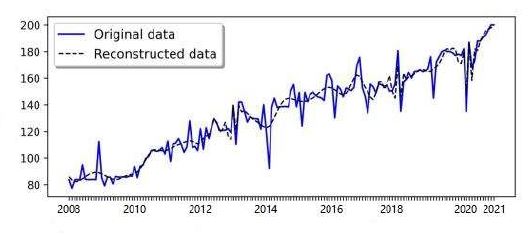
In this section, wavelet decomposition is applied to the monthly throughput data of Qingdao Port collected from 2008 to 2021, resulting in 168 data samples. The data was preprocessed to become smoother by applying wavelet decomposition at level 2 and reconstructed to obtain a new dataset. The original data is presented in Figure 4, and the performance of the wavelet decomposition is shown in Figures 5 and 6. The pattern appeared much smoother than the original one, considering the reconstruction step already included filters, which eliminated the high-frequency patterns.
Then, a hybrid approach called PSO-ESN was implemented to provide forecasting data for container throughput. Compared to the traditional ESN approach, the hybrid approach improved the effectiveness by exploring the adjacent areas of the current result for a better one. The training dataset considered 134 samples from the original data, and the performance was tested on the remaining 34 samples. In the ESN, the number of neurons in the dynamic reserve pool was 100, and the spectral radius of the matrix was set to 0.6.
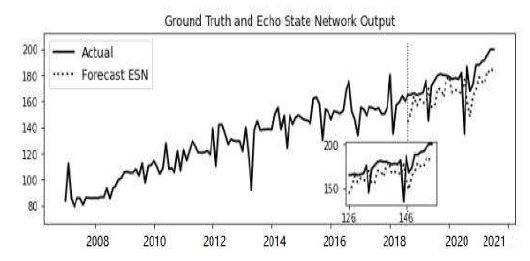
Figures 7 and 8 show the results of the pure ESN and hybrid PSO-ESN methods, respectively, with the error comparison displayed in Table 1.
The root means square error (RMSE) evaluation method in Table 1 shows that with the improvement of the PSO algorithm, the accuracy of the ESN model improved from 0.1631 to 0.0862. Through statistical data comparison, the prediction model based on the PSO-improved ESN exhibited the best performance in the prediction model of Qingdao Port container throughput.
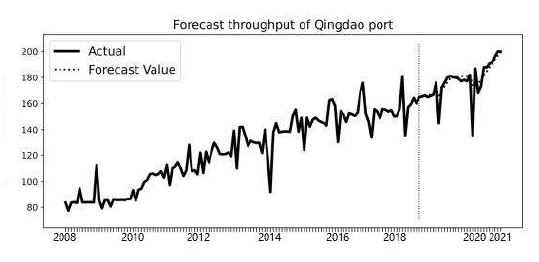
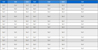
The established model was used to predict the container throughput of Qingdao Port from 2022 to 2024, and the results are shown in Table 2.
As seen in Table 2, the container throughput in 2022 and 2023 shows an upward trend; however, the container throughput in 2024 decreases slightly. The forecast data is only for the reference of the port staff.
4. Conclusion
Owing to the development of global economic integration, ports have become important nodes in the logistics supply chain as the hub of comprehensive transportation. As an important part of port planning, the predicted throughput of port containers has influenced the planning and decision making of governments in various countries. Simultaneously, the prediction of port throughput can help the port identify problems and sources. This study proposed a novel method for predicting the port container throughput. Considering the characteristics of the container throughput time series, the container throughput series was decomposed and reconstructed by a wavelet to obtain the approximate and detailed parts. Wavelet decomposition provides less noisy data, thereby improving performance prediction. Then, combined with the good nonlinear prediction effect of the ESN, the prediction result was calculated using the ESN prediction. Furthermore, an additional optimization algorithm was proposed, which used the improved particle swarm optimization algorithm to dynamically select part of the random weights of the echo state network. As a result, the prediction accuracy and generalization performance were improved. First, we searched for the ESN best parameters using the PSO approach; subsequently, we used the ESN pair to predict the port container throughput. The simulation results showed that the prediction method exhibited a good prediction ability. Therefore, we intend to highlight this prediction in future studies to provide better suggestions for port development.
Acknowledgments
This research was supported by the 4th Educational Training Program for the Shipping, Port, and Logistics from the Ministry of Oceans and Fisheries.
This paper is an expanded version of the proceeding paper entitled “Research On The Prediction Of Container Throughout Of Qingdao Port Using Based On Echo State Network Optimized By Improved Particle Swarm Algorithm” presented at the ICACE 2022.
Author Contributions
Conceptualization, Z. Qu and H. Kim; Methodology, Z. Qu and S. Lee; Software, Z. Qu; Validation, Z. Qu and H. Kim; Formal Analysis, Z. Qu and L. N. B. Long; Investigation, Truong Ngoc Cuong; Resources, Z. Qu and S. Lee; Data Curation, Z. Qu, Truong Ngoc Cuong, L. N. B. Long; Writing-Original Draft Preparation, Z. Qu; Writing-Review & Editing, H. Kim; Visualization, Z. Qu; Supervision, H. Kim; Project Administration, H. Kim; Funding Acquisition, H. Kim.
References
-
S. -C. Park, S. -S. Kang, J. -H. Yoon, and G. -Y. Kim, “The prediction of fatigue life of muffler by artificial neural network,” Journal of the Korean Society of Marine Engineering, vol. 37, no. 8, 2013 (in Korean).
[https://doi.org/10.5916/jkosme.2013.37.8.869]

-
Y. Zhang and L. Zhao, “Time series forecasting based on echo state network optimized by improved particle swarm algorithm,” Computer Science & Application, vol. 11, no. 8, pp. 2070-2079, 2021 (in Chinese).
[https://doi.org/10.12677/CSA.2021.118212]

-
J. H. Lee, S. -Y. Yoo, S. Shin, D. -H. Kang, S. Lee, and J. C. Lee, “Fault diagnosis of bearings using machine learning algorithm,” Journal of Advanced Marine Engineering and Technology, vol. 43, no. 6, pp. 455-462, 2019.
[https://doi.org/10.5916/jkosme.2019.43.6.455]

-
M. Laner, P. Svoboda, and M. Rupp, “Parsimonious fitting of long-range dependent network traffic using ARMA models,” IEEE Communications Letters, vol. 17, no. 12, pp. 2368-2371, 2013.
[https://doi.org/10.1109/LCOMM.2013.102613.131853]

-
C. Narendra Badu and B. Eswara Reddy, “A moving-average filter based hybrid ARIMA-ANN model for forecasting time series data,” Applied Soft Computing, vol. 23, pp. 27-38, 2014.
[https://doi.org/10.1016/j.asoc.2014.05.028]

-
Y. -J. Jung, S. Kang, D. Doh, “Forecasting earning of VLCC tankers using artificial neural networks,” Journal of the Korean Society of Marine Engineering, vol. 42, no. 10, pp. 851-858, 2018.
[https://doi.org/10.5916/jkosme.2018.42.10.851]

- K. Li, Y. Han, and H. J. Huang, “Chaotic time series prediction based on IBH-LSSVM and its application to short-term prediction of dynamic fluid level of the oil wells,” Information and Control, vol. 45, no. 2, pp. 241-247.
- K. Xue, U. Zhou, Y. Ping, Y. Guo, and F. Yang, “P2P traffic prediction model based on wavelet transform and ESN,” Computer Engineering and Design, vol. 34, no. 4, pp. 1147-1152, 2013.
-
N. Chouikhi, B. Ammar, N. Rokbani, and A. M. Alimi, “PSO-based analysis of echo state network parameters for time series for ecasting,” Applied Soft Computing, vol. 55, pp. 211-225, 2017.
[https://doi.org/10.1016/j.asoc.2017.01.049]

-
A. Jamal, M. A. H. Ashour, R. Helmi, and S. L. Fong, “A wavelet - neural networks model for time series,” 2021 IEEE 11th IEEE Symposium on Computer Applications & Industrial Electronics (ISCAIE), pp. 325-330, 2021.
[https://doi.org/10.1109/ISCAIE51753.2021.9431777]

- M. T. I. S. Al Wadia and M. T. Ismail, “Selecting wavelet transforms model in forecasting financial time series data based on ARIMA model,” Applied Mathematical Sciences, vol. 5, no. 7, pp. 315-326, 2011.
-
P. Areekul, T. Senjyu, N. Urasaki, and A. Yona, “Neural-wavelet approach for short term price forecasting in deregulated power market,” Journal of International Council on Electrical Engineering, vol. 1, no. 3, 2011.
[https://doi.org/10.5370/JICEE.2011.1.3.331]

- H. Wei, H. Ye, and X. Hui, “Internet traffic prediction based on wavelet neural network,” Computer Science, vol. 38, no. 10A, 2011.
-
H. Jaeger and H. Haas, “Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication,” Science, vol. 304, no. 5667, pp. 78-80, 2004.
[https://doi.org/10.1126/science.1091277]

-
H. Wang and X. Yan, “Optimizing the echo state network with a binary particle swarm optimization algorithm,” Knowledge-Based Systems, vol. 86, pp. 182-193, 2015.
[https://doi.org/10.1016/j.knosys.2015.06.003]

- P. Yu, W. Jianmin, and P. Xiyuan, “Time series prediction based on echo state network,” Acta Electronica Sinica, vol. 38, 2010.
- R. Tiaojuan, Z. Chenjian, L. Banteng, Z. Qihang, “Prediction of nonlinear time series based on elastic small-world echo state network,” Computer Applications and Software, vol. 33, no. 4, 2012.
-
D. Li, F. Liu, J. Qiao, and R. Li, “Structure optimization for echo state network based on contribution,” Tsinghua Science and Technology, vol. 24, no. 1, pp. 97-105, 2019.
[https://doi.org/10.26599/TST.2018.9010049]

- S. Bodi, Z. Shudong, and H. Qi, “Roughness prediction model based on improved particle swarm optimization neural network,” Modular Machine Tool and Automatic Machining Technology, vol. 33, no. 4, 2011.