Optimal power-splitting protocol in the wireless relay networks
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this study, power-splitting relaying is considered for decode-and-forward (DF)-based relay networks, which consist of a source, relay, and destination, and harvest energy from the radio frequency (RF) radiation of the source. To minimize outage probabilities, we analytically derive the optimal power ratio of power splitting for DF relaying in closed-form and present the exact expression of outage probability with an optimal ratio over Rayleigh fading channels. Therefore, this paper proposes Relay Selection of Optimal Power Splitting(RSOPS), an optimal power-splitting relay selection scheme that maximizes the achievable transmission rate between the source and destination and can be used on a Simultaneous Wireless Information and Power Transfer(SWIPT) system. RSOPS selects the “Best” relay that maximizes the achievable transmission rate and demonstrates a significantly reduced outage probability. The outage probability expression with the optimal ratio is validated using the numerical results. The optimal power-splitting relaying is compared to other power-splitting protocols with a fixed power-splitting ratio.
Keywords:
Energy harvesting, Energy management, Energy efficiency, Power generation control, Radio frequency, IoT1. Introduction
Energy harvesting is a promising solution that can help prolong the viability of wireless networks, including ad-hoc networks, cellular networks, and sensor networks, which are constrained by limitations, such as batteries that cannot be replaced easily. Conventional energy-harvesting technologies derive energy from the surrounding environment, such as solar and wind energy. However, renewable energy sources cannot be controlled, and it is difficult to maintain a stable energy supply using these sources. Wireless energy transfer has recently attracted significant attention as a new energy-harvesting source. With this technology, a receiver antenna captures radio-frequency (RF) radiation and converts it into energy. This technology allows wireless signals to carry both information and energy. In this study, we propose two practical schemes for simultaneous wireless information and power transfer (SWIPT) using RF radiation: time switching [1] and power splitting [2]. In power splitting, the signal received from the source is split into energy and information at the receiver. In the case of time switching, the receiver switches between decoding information and harvesting energy.
Energy harvesting is significant in the case of wireless relay communication because relay nodes consume their energy to facilitate transmission from the source to the destination, and the energy may be exhausted rapidly. Recent studies have focused on energy harvesting using RF signals in relaying communication [3]-[11]. Nasir et al. investigated the ergodic capacity and outage probability of time-switching and power-splitting protocols for amplify-and-forward (AF) relaying [3]. In [4], the authors also analyzed the throughput and ergodic capacity of two different protocols for decode-and-forward (DF) relaying. In [5], SWIPT was investigated in cognitive radio networks. Chen et al. evaluated the outage probability where AF relaying was operated for a two-way relay with SWIPT [6]. Chalise et al. investigated the performance of AF multiple-input-multiple-output relay systems with an energy-harvesting receiver [7]. Strategies for power allocation between multiple source and destination pairs with an energy-harvesting relay node were studied in [8]. The authors of [9] and [10] assessed AF and DF relaying and numerically evaluated the maximum achievable throughput. The optimal ratio of power splitting forAF relaying is analytically derived in the closed form [11].
In this study, we derive the optimal power allocation ratio of power splitting for DF relaying as closed-form and formulate the exact expression for outage probability at an optimal ratio over Rayleigh fading channels. To the best of our knowledge, no study has derived the exact expression for outage probability for DF relaying communication that adopts a power-splitting protocol with an optimal power ratio. Thus, we derive the optimal power allocation ratio as closed-form and evaluate the exact outage probability with an optimal value when the power-splitting protocol is applied to a DF relay consisting of a source, relay, and destination. The remainder of this paper is organized as follows. Section 2 describes the proposed system. Section 3 describes the proposed optimal power-splitting relay technology and the performance of the proposed scheme, using a simulation. Section 4 presents the simulation results, and Section 5 presents the conclusions.
2. System model
In this work, we consider a wireless network that consists of a source, destination, and N relays, without any source-destination link, as shown in Figure 1. The relay does not use a power supply; instead, it uses a rechargeable battery that can harvest energy from radio frequency (RF) signals that are broadcast by the source. It is assumed that each network node has a single antenna that communicates with a half-duplex constraint so that the node can transmit and receive data in succession but not simultaneously. A relay involves DF relaying, decoding the signal from the source, and forwarding it to the destination.
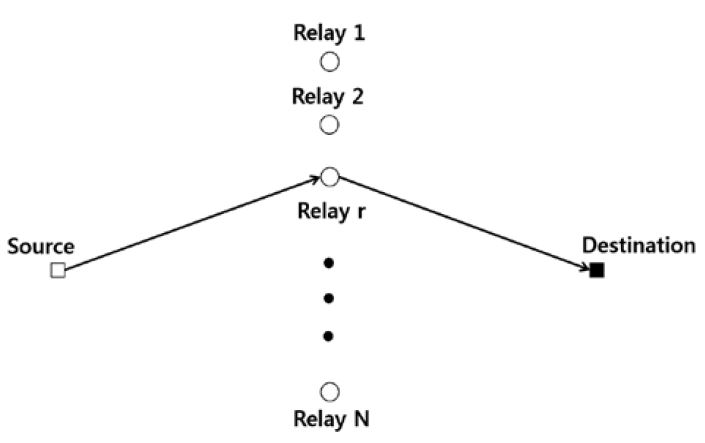
Power-splitting protocol model: The wireless network consists of a source, a destination, and N relays
We denote the source, relay, and destination as s, r, and d, respectively. The channel fading model is assumed to be a block Rayleigh fading channel that is fixed over one block time T. Each complex channel coefficient hij between nodes i and j is independent of hij ~ CN(0,λij). We also assume that the variance of all additive white Gaussian noises at the relay and destination is one. The notation γij expresses the effective channel gain, which is the squared magnitude of the channel coefficient. Each channel has a reciprocal; therefore, the channel gain from node i to j is the same as that from node j to i, that is, γij = γji
3. Relay Selection of Optimal Power Splitting (RSOPS)
In this section, we derive the optimal power allocation ratio for power-splitting relaying, describe a novel approach for relay selection of SWIPT in a distributed manner, and analyze the outage probability of cooperative transmission, called RSOPS. In the proposed scheme, only one “Best” relay to cooperate transmission has the maximum achievable data rate with optimal power allocation ratio among N available relays in the distributed manner. By considering not only the channel gain coefficient between nodes but also the channel condition, energy harvesting, and power allocation of the received RF signal, we exploit the characteristics of SWIPT for relay selection: RSOPS has a better performance compared to other relay selection schemes with fixed power allocation ratios, such as random relay selection, relay selection based on maximum end-to-end channel gain coefficient, partial relay selection, and relay selection based on maximum end-to-end signal-to-noise.
3.1 Operation of RSOPS
The following assumptions are required to describe the RSOPS scheme concisely:
- ① Every relay is placed within the one-hop transmission range of the source and destination. Hence, any relay can communicate directly with the source and destination if they are in the same system. This also means that the channel gain between the source or destination and any relay is nonzero.
- ② The receiver has channel gain from the received data, whereas the transmitter does not. This assumption is practical in most wireless networks.
- ③ Relays record the value of the optimal power allocation parameter in the flag packet.
The above two assumptions make it possible for every relay to obtain the channel gain coefficients between the source and its self-destination after exchanging the RTS and CTS. According to the third assumption, relays can transmit the value of the optimal power allocation parameter to the source when the cooperator uses it. In [12] and [13], a transmitter sent an RTS/CTS before data transmission, and in [14], a selected relay sent a flag packet to notify the relay selection. The last assumption was motivated by [13] and [15]. How the relay provides feedback on the optimal power allocation parameter into the flag packet to the source is a different research issue, which is beyond the scope of this study. Although this assumption requires additional bits in the flag packet, which is used for relay contention, it can improve the network performance. Based on the obtained local network channel gains, each relay calculates the value of the optimal power allocation parameter and the maximum achievable rate as if it were selected as a cooperator. The maximum achievable rate is used in the relay contention period to determine the “Best” relay, which requires the maximum achievable rate among all available relays.
The overall communication procedure for the RSOPS follows the algorithm described below. (See Figure 2.)
- ① The source sends an RTS packet to the destination via broadcast. Each relay overhears the information in the RTS and estimates the instantaneous channel gain between the source and the relay.
- ② The destination feeds the CTS back to the source. Each relay overhears the information in the CTS and estimates the instantaneous channel gain between the relay and the destination.
- ③ After exchanging the RTS and CTS, each relay has information related to the channel gain values between the source and relay and between the relay and destination. Each relay then calculates the optimal power allocation ratio and the maximum achievable rate when the SWIPT protocol is self-operated.
- ④ The relays set their backoff counters to an initial value (Tr) based on the maximum achievable rate (Re2e,r). When the counter decreases to zero, the relays wait in the listening mode. As soon as the backoff counter expires, the relay broadcasts a short flag packet with the optimal power allocation ratio value to contend for and occupy the role of a cooperator.
- ⑤ The first relay that broadcasts a flag packet is determined to be a cooperator. Other relays that receive the flag packet in listening mode are silent. The source and selected relays collaboratively transmitted data to the destination. The algorithm returns to Step 1.
| (1) |
where is the maximum achievable rate, and the source and destination communication are assisted by relay r. The method used to determine and calculate is described in the following subsection. In calculating Tr , α is a constant and is determined by considering and physical aspects. Usually, α has a value on the order of microseconds or nanoseconds. According to Equation (1), the initial value of the backoff counterTr, becomes larger as the calculated maximum achievable rate decreases. Therefore, the counter of the relay with the largest maximum achievable rate expires first. As soon as the counter becomes zero, the corresponding relay records the value of the optimal power allocation to the flag packet and broadcasts the flag packet to occupy the location of the cooperator. If the relays receive a flag that originates from another node in listening mode, they drop the received packet and reset the counter for the subsequent data packet transmission. A relay with the largest maximum achievable rate is chosen using this relay-selection procedure as a cooperator.
3.2 Optimal power allocation ratio at each relay
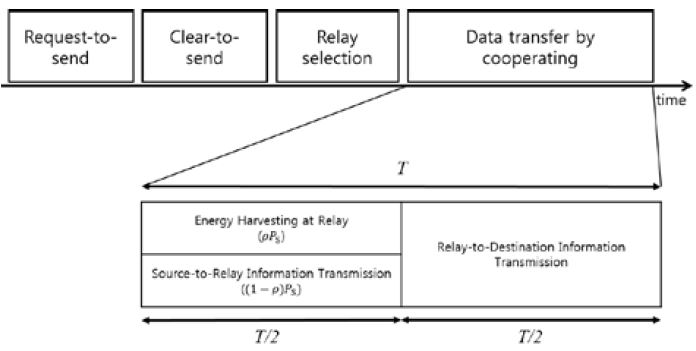
In this section, we describe the operation of the power-splitting protocol and analytically derive the optimal splitting power allocation in a closed form. In the power-splitting protocol, the block time T is divided into source transmission and relay transmission parts, as shown in Figure 2. First, the source transmits the RF signals to the relay over T/2 time duration. The relay then splits the RF signals into a harvesting energy part and a decoding information part based on the power ratio ρ. The relay retransmits the decoded information to the destination for the remaining time block duration. The energy from the ρ proportion of the received power is harvested at the relay, and 1 − ρ proportion of the received power is used for decoding information from the source.
Let Rsr denote the transmission rate between the source and relay r . Because only 1 − ρ fraction of the received power is used for information decoding, Rsr is calculated by [16].
| (2) |
where Ps is the transmission power at the source and γsr denotes the effective channel gain between the source and relay r, which is the squared magnitude of the channel coefficient. Because the ρ fraction of the received power is used for harvesting energy at the relay, the harvested energy at the relay during T/2 time is expressed as follows:
| (3) |
where η (0 < η < 1) is the energy-conversion efficiency factor, which depends on the rectifier and energy-harvesting circuitry. After the source transmission duration, the relay retransmits the decoded information to the destination by using the energy harvested over the first T/2 time block. Thus, the transmission power Pr at the relay is.
| (4) |
As shown in Equation (2), the transmission rate between the relay and destination is calculated as follows:
| (5) |
where γrd denotes the effective channel gain between the relay and the destination. Thus, the achievable end-to-end transmission rate between the source and destination is
| (6) |
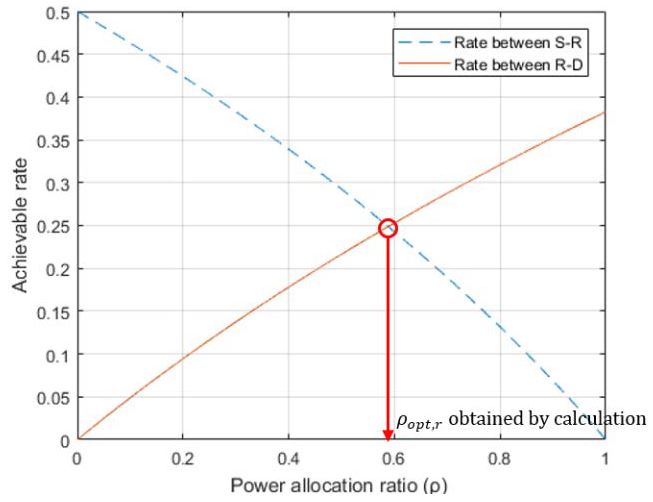
In Equations (2) and (5), the transmission rate between the source and relay is a monotonically increasing function over ρ. By contrast, the transmission rate between the relay and destination is a monotonically decreasing function over ρ . Therefore, the two transmission rates in Equation (6) should have the same value to maximize the achievable end-to-end transmission rate. If ρopt,r denotes the optimal value that enables the maximum achievable end-to-end transmission rate at relay r ; it can be calculated as follows:
| (7) |
The optimal closed-form power allocation ratio at relay r in Equation (7) is shown in Figure 3.
3.3 Analysis of outage probability
In this section, we first formulate the exact expression of the outage probability at the optimal power allocation obtained in the previous subsection over Rayleigh fading channels. To correctly decode the information received from the transmitter, the transmission rate should be larger than the spectral efficiency, R bps/Hz. Suppose the achievable end-to-end transmission rate between the source and destination in Equation (6) is smaller than the spectral efficiency. In that case, the destination cannot decode data from the source, and an outage occurs. Thus, the outage probability Pout is expressed as follows:
| (8) |
where is the maximum achievable end-to-end transmission rate at relay r, which is the achievable end-to-end transmission rate at relay r with optimal power allocation. The outage probability with optimal power allocation when the source selects relay r to cooperate, , is given by
| (9) |
where βr = λsr(22R − 1)/ηPs and Kν(∙) is the second kind of modified Bessel function with order v.
Relay selection is performed by comparing the of each relay node as a backoff timer method. The outage probability at each relay can be derived from these results. The outage probability of the RSOPS can be easily derived from the outage probability at each relay. An outage occurs in the RSOPS only if every cooperative transmission via each relay fails. That is, the maximum achievable end-to-end transmission rate at any relay is smaller than the spectrum efficiency R. Thus, the outage probability of the RSOPS, Pout, is given by
| (10) |
If the relay network is a hetero-network, where the expected value of the channel gain coefficient between the source and any relay is the same, and the expected value of the channel gain coefficient between the destination and any relay is the same (that is γs1 = ⋯ = γsr= ⋯ = γsN and γ1d= ⋯ = γrd = ⋯ = γNd), then the outage probability of the RSOPS is given by
| (11) |
where β = λsr(22R − 1)/ηPs.
4. Performance evaluation
In this section, we first investigate the optimal power-splitting relaying with only one relay. The performance of the power-splitting protocol at the optimal power allocation is presented through numerical results and is compared with the performance of the power-splitting protocols at a fixed power ratio. To validate the accuracy of the outage probability derived in Equation (9), we simulate a power-splitting protocol at an optimal power ratio that is obtained by exhaustively searching for the parameter ρ over the range [0, 1]. The simulation of power-splitting relaying by an exhaustive search confirms that the analytical results obtained in Equation (9) demonstrate the same performance as the numerical results. A system model consisting of one source, one relay, and one destination was adopted for the performance evaluation with one relay. The energy conversion efficiency coefficient η = 70%. For convenience, the time duration of each transmission block T was set to one. The required rate, R, was set to 1 dB. For comparison, a power-splitting protocol with fixed power allocation (ρ = 0.1, 0.3, 0.5, 0.7, 0.9) was considered. The simulations were derived from ten million iterative samples (the channel realization trial was a million times).
Figure 4 compares the outage probabilities of optimal power-splitting relaying to the fixed allocation ratio power-splitting relaying when the link between the source and relay and the link between the relay and destination have unit variance Rayleigh fading, that is, λsr= λrd = 1. As shown in Figure 4, the optimal power splitting relaying outperforms fixed-ratio protocols. In optimal power-splitting relaying, because the power allocation parameter ρopt is calculated based on the channel conditions and the conversion efficiency for every block duration, the optimal power-splitting relaying has a lower outage probability than the fixed-ratio protocols for the entire displayed range of the source‘s transmission power values.
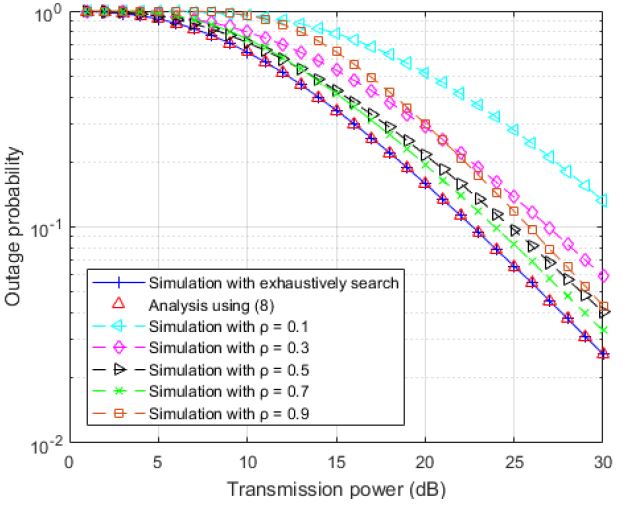
Outage probability of optimal power-splitting relaying and fixed-ratio power-splitting relaying at different source transmission power values
Figure 5 shows the outage probabilities with increasing expected channel coefficient values between the relay and destination, λrd, to observe the distinction between the optimal power-splitting relaying and fixed-ratio protocols when the variance value of the link between the source and relay is two and the transmission power of the source is set to 10 dB. As shown in Figure 5, protocols with lower ρ values demonstrate a significant performance improvement. On the other hand, there is a slight decrease in the outage probability with higher ρ value protocols, as the expected channel coefficient value between the relay and destination increases. This is because the optimal value obtained in Equation (7) is lower, as the channel link between the relay and destination has a higher coefficient value. However, the optimal power-splitting relaying outperformed the fixed ratio protocols and demonstrated a significant performance improvement with increasing channel coefficient values for the same reasons explained in the discussion of Figure 4.
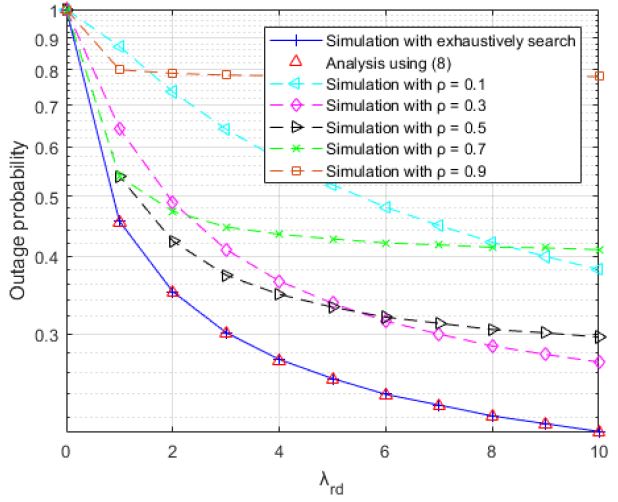
Outage probability of optimal power-splitting relaying and fixed ratio power-splitting relaying at different expected channel coefficient values of relay and destination.
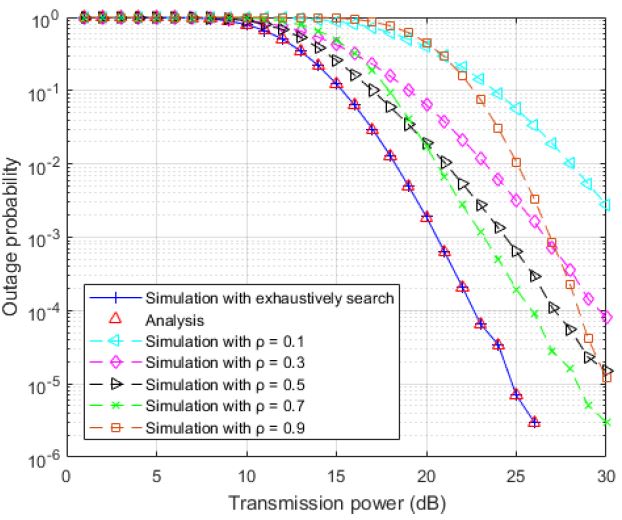
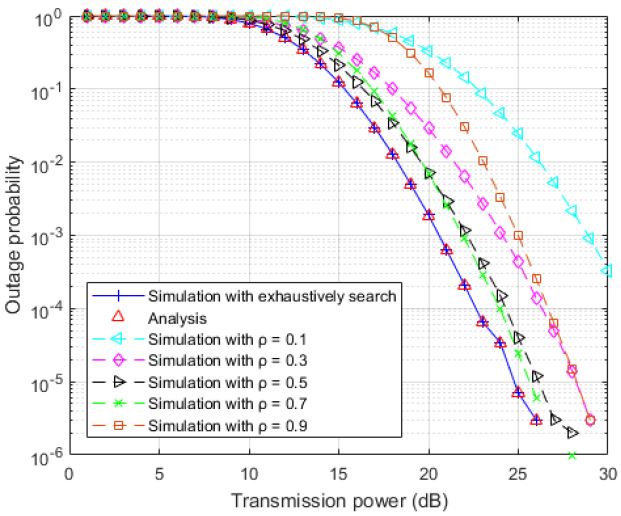
In Figures 6-9, the performances of the proposed RSOPS scheme are presented using numerical results, which are compared to other relay selection criteria, such as random relay selection [17][18], relay selection based on the maximum harvested energy [19], opportunistic relay selection [20], and relay selection based on the maximum signal-to-noise ratio in the compared relay selection schemes [21] previously mentioned in Section 3 To validate the accuracy of the outage probability derived in Equation (10), we simulate the RSOPS at an optimal power ratio, which is obtained by exhaustively searching for the parameter ρ over the range [0, 1] at each relay. The simulation of the RSOPS by an exhaustive search confirms that the analytical results obtained in Equation (10) demonstrate the same performance as the numerical results. A system model consisting of one source and one destination pair with N available relays was adopted for performance evaluation. We assume that N = 8 relays are the cooperators. The energy conversion efficiency coefficient was set to η = 70%. For convenience, the time duration of each transmission block T was set to one. For convenience, all of the links have unit variance Rayleigh fading, that is, λ_ij = 1 for any i,j in Figures 6-7. The required rate, R, was set to 2 dB. The performance metric to be compared was the average outage probability. For comparison, various fixed power allocation ratios (ρ = 0.1, 0.3, 0.5, 0.7, 0.9) for other relay selections were considered. After exchanging the RTS packet from the source and CTS packet from the destination, the system selects the “Best” relay during the relay contention period in a distributed manner by setting a backoff timer at each relay. Then, the source and the best-selected relay cooperate for data transmission to the destination in power-splitting relaying. The simulations were derived from ten million iterative samples (the channel realization trial was a million times).
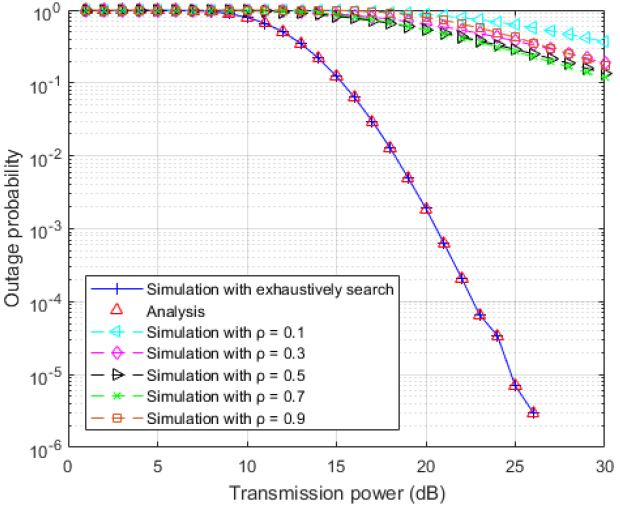
Outage probability of RSOPS and fixed ratio random relay selection at different source transmission power values

Outage probability of RSOPS and fixed ratio relay selection based on maximum harvested energy at different source transmission power values
Figures 6 and 7 compare the outage probability of the RSOPS with random relay selection and relay selection based on the maximum harvested energy at fixed power allocation ratios (ρ = 0.1, 0.3, 0.5, 0.7, 0.9). There is a significant performance gap between the proposed RSOPS, random relay selection, and relay selection based on the maximum harvested energy. The performance of random relay selection is the lowest because it is the simplest relay selection and does not consider choosing a cooperator. In addition, relay selection based on the maximum harvested energy has poor network performance because it considers only the channel gain coefficient between the source and relay. The performance difference according to different fixed power allocation ratios in the random relay selection and the relay selection based on the maximum harvested energy is similar to that described later. We explain it in the next paragraph in Figure 9.
Figures 8 and 9 show the outage probability of the RSOPS, opportunistic relay selection, the outage probability of the RSOPS, and relay selection based on the signal-to-noise ratio at fixed power allocation ratios (ρ = 0.1, 0.3, 0.5, 0.7, 0.9). In Figure 8, the opportunistic relay selection selects the ‘Best relay’ based on the maximum end-to-end channel gain coefficient. Although opportunistic relay selection is most widely used for relay selection in cooperative communication, it does not consider the characteristics of SWIPT; that is, the link between the source and relay is used not only for data transmission but also for energy transfer. Thus, opportunistic relay selection is not suitable as a relay selection method for SWIPT.
Outage probability of RSOPS and fixed ratio opportunistic relay selection at different source transmission power values.
Outage probability of RSOPS and fixed ratio relay selection based on signal-to-noise ratio at different source transmission power values.
In Figure 9, the relay selection based on signal-to-noise ratio selects the ‘Best relay’ based on the maximum end-to-end signal-to-noise ratio, which is a modified version of opportunistic relay selection for SWIPT. We can see that the simulation with fixed ratios of 0.5 and 0.7 has superior performance compared to other fixed ratios because it is merely the expected channel gain value between the relay and destination. The expected channel gain value between the relay and destination is set by 1, and the fixed ratios 0.5 and 0.7 are close to ρ_(opt,r) value with γ_rd = 1. Relay selection based on the maximum end-to-end signal-to-noise ratio considers the characteristics of SWIPT to some degree; therefore, the achievable end-to-end rate in Equation (6) is used for relay selection. However, relay selection based on the signal-to-noise ratio only uses fixed power allocation because the source needs centralized information about all links between nodes for optimal power allocation. This problem can be easily solved by adding some bits to a flag packet broadcast from the relay. Each relay calculates the optimal power allocation and inputs the value into the flag packet to be sent. This procedure eliminates the need for a source to collect information about all links. Owing to the reasons explained above, the RSOPS has a lower outage probability than other relay selection schemes for the entire displayed range of SNR values.
5. Conclusion
In this paper, we propose RSOPS, an optimal power-splitting relay selection scheme, that maximizes the achievable transmission rate between the source and destination and can be used on a SWIPT system. The RSOPS advantageously utilizes the SWIPT characteristics and delivers the optimal power allocation parameter at each relay in a distributed manner. The RSOPS selects the “Best” relay that maximizes the achievable transmission rate and demonstrates a significantly reduced outage probability. In addition, the RSOPS is carried out in a distributed manner that does not require complicated centralized control. We theoretically analyzed the optimal power allocation ratio, the outage probability at each relay, and the outage probability of RSOPS as closed-form over the Rayleigh fading channel. The performance of the RSOPS was evaluated, and the numerical results showed significant improvements in outage probability compared to other fixed-ratio relay selection schemes.
Acknowledgments
This work was supported by a grant from 2017 Research Fund(Research Professor) of Andong National University.
Author Contributions
Conceptualization, S. G. Kim and J. H. Kim; Methodology, S. G. Kim; Software, J. H. Kim; Validation, S. G. Kim and J. H. Kim; Formal Analysis, J. H. Kim; Investigation, S. G. Kim; Resources, S. G. Kim; Data Curation, S. G. Kim; Writing—Original Draft Preparation, S. G. Kim and J. H. Kim; Writing—Review & Editing, J. H. Kim; Visualization, S. G. Kim; Supervision, J. H. Kim; Project Administration, J. H. Kim; Funding Acquisition, S. G. Kim and J. H. Kim.
References
-
P. Grover and A. Sahai, “Shannon meets tesla: Wireless information and power transfer,” Proceedings of International Symposium on Information Theory (ISIT), pp. 2363-2367, 2010.
[https://doi.org/10.1109/ISIT.2010.5513714]

-
L. R. Varshney, “Transporting information and energy simultaneously,” Proceedings of International Symposium on Information Theory (ISIT), pp. 1612-1616, 2008.
[https://doi.org/10.1109/ISIT.2008.4595260]

-
A. A. Nasir, X. Zhou, S. Durrani, and R. A. Kennedy, “Relaying protocols for wireless energy harvesting and information processing,” IEEE Transactions on Wireless Communications, vol. 12, no. 7, pp. 3622-3636, 2013.
[https://doi.org/10.1109/TWC.2013.062413.122042]

-
A. A. Nasir, X. Zhou, S. Durrani, and R. A. Kennedy, “Throughput and ergodic capacity of wireless energy harvesting based DF relaying network,” Proceedings of IEEE International Conference on Communications (ICC), pp. 4066-4071, 2014.
[https://doi.org/10.1109/ICC.2014.6883957]

-
S. Lee, R. Zhang, and K. Huang, “Opportunistic wireless energy harvesting in cognitive radio networks,” IEEE Transactions on Wireless Communications, vol. 12, no. 9, pp. 4788-4799, 2013.
[https://doi.org/10.1109/TWC.2013.072613.130323]

-
Z. Chen, B. Xia, and H. Liu, “Wireless information and power transfer in two-way amplify-and-forward relaying channels,” Proceedings of IEEE Global Conference on Signal and Information Processing (GlobalSIP), pp. 168-172, 2014.
[https://doi.org/10.1109/GlobalSIP.2014.7032100]

-
B. K. Chalise, W. K. Ma, Y. D. Zhang, H. Suraweera, and M. G. Amin, “Optimum performance boundaries of OSTBC based AF-MIMO relay system with energy harvesting receiver,” IEEE Transactions on Signal Processing., vol. 61, no. 17, pp. 4199-4213, 2013.
[https://doi.org/10.1109/TSP.2013.2265224]

-
Z. G. Ding, S. M. Perlaza, I. Esnaola, and H. V. Poor, “Power allocation strategies in energy harvesting wireless cooperative networks,” IEEE Transactions on Wireless Communications, vol. 13, no. 2, pp. 846-860, 2014.
[https://doi.org/10.1109/TWC.2013.010213.130484]

-
A. Minasian, S. ShahbazPanahi, and R. S. Adve, “Energy harvesting cooperative communication systems,” IEEE Transactions on Wireless Communications, vol. 13, no. 11, pp. 6118-6131, 2014.
[https://doi.org/10.1109/TWC.2014.2320977]

-
C. Huang, R. Zhang, and S. Cui, “Throughout maximization for the Gaussian relay channel with energy harvesting constraints,” IEEE Journal on Selected Areas in Communications, vol. 31, no. 8, pp. 1469-1479, 2013.
[https://doi.org/10.1109/JSAC.2013.130811]

-
S. Atapattu and J. Evans, “Optimal power-splitting ratio for wireless energy harvesting in relay networks,” Proceedings of IEEE Vehicular Technology Conference (VTC2015-Fall), pp. 1-6, 2015.
[https://doi.org/10.1109/VTCFall.2015.7391056]

-
A. Bletsas, A. Khisti, D. P. Reed, and A. Lippman, “A simple cooperative diversity method based on network path selection,” IEEE Journal on Selected Areas in Communications, vol. 24, no. 3, pp. 659-672, 2006.
[https://doi.org/10.1109/JSAC.2005.862417]

-
Z. Zhou, S. Zhou, J. -H. Cui, and S. Cui, “Energy-efficient cooperative communication based on power control and selective single-relay in wireless sensor networks,” IEEE Transactions on Wireless Communications, vol. 7, no. 8, pp. 3066-3078, 2008.
[https://doi.org/10.1109/TWC.2008.061097]

-
P. Liu, Z. Tao, Z. Lin, E. Erkip, and S. Panwar, “Cooperative wireless communications: a cross-layer approach,” IEEE Transactions on Wireless Communications, vol. 13, no. 4, pp. 84-92, 2006.
[https://doi.org/10.1109/MWC.2006.1678169]

-
S. R. Khosravirad, L. Szczecinski, and F. Labeau, “Rate adaptation for cooperative HARQ,” IEEE Transactions on Wireless Communications, vol. 62, no. 5, pp. 1469-1479, 2014.
[https://doi.org/10.1109/TCOMM.2014.031614.130685]

-
M. Ju, K. -M. Kang, K. -S. Hwang, and C. Jeong, “Maximum transmission rate of PSR/TSR protocol in wireless energy harvesting DF-based relay networks,” IEEE Journal on Selected Areas in Communications, vol. 33, no. 12, pp. 2701-2717, 2015.
[https://doi.org/10.1109/JSAC.2015.2481213]

-
P. N. Son and H. Y. Kong, “Energy-harvesting relay selection schemes for decode-and-forward dual-hop networks,” IEICE Transactions on Communications, vol. E98-B, no. 12, pp. 2485–2495, 2015.
[https://doi.org/10.1587/transcom.E98.B.2485]

-
Z. Ding, I. Krikidis, B. Sharif, and H. Poor, “Wireless information and power transfer in cooperative networks with spatially random relays,” IEEE Transactions on Wireless Communications, vol. 13, no. 8, pp. 4440-4453, 2014.
[https://doi.org/10.1109/TWC.2014.2314114]

-
J. Yan, C. Zhang, and Z. Gao, “Distributed relay selection protocols for simultaneous wireless information and power transfer,” Proceedings of IEEE 25th Annual International Symposium on Personal, Indoor, and Mobile Radio Communication (PIMRC), pp. 474-479, 2014.
[https://doi.org/10.1109/PIMRC.2014.7136212]

-
K. -H. Liu, “Performance analysis of relay selection for cooperative relays based on wire-less power transfer with finite energy storage,” IEEE Transactions on Vehicular Technology, vol. 65, no. 7, pp. 5110-5121, 2016.
[https://doi.org/10.1109/TVT.2015.2469300]

-
D. S. Michalopoulos, H. A. Suraweera, and R. Schober, “Relay selection for simultaneous information transmission and wireless energy transfer: A tradeoff perspective,” IEEE Journal on Selected Areas in Communications, vol. 33, no. 8, pp. 1578-1594, 2015.
[https://doi.org/10.1109/JSAC.2015.2391771]

-
D. -J. Kim and D. -W. Seo, “Energy-efficient simultaneous wireless information and power transfer-enabled orthogonal multiple access under distributed antenna systems,” Journal of Advanced Marine Engineering and Technology, vol. 46, no. 4, pp. 196-203, 2022.
[https://doi.org/10.5916/jamet.2022.46.4.196]