Review of the optimal locations of coastal sea area for operating wave energy converter in Korea
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
To improve the efficiency of wave energy converters during operation, their shape and geometrical form should be optimized considering the environment of the sea area where they will be installed. However, prior studies on the operation and efficiency improvement of domestic ocean wave generators have been conducted based only on a single or specific sea area. For this reason, several sea areas that can represent the West Sea, South Sea, and East Sea of Korea were selected from ocean data buoys installed in the domestic sea. By applying the Rayleigh distribution using the observed time series data, the probability distributions of the maximum wave height, significance wave height, average wave height, and peak wave period for each sea area were analyzed. Finally, based on the Rayleigh distribution results for the wave heights of each sea area, the optimal sea areas on the domestic coast for operating wave energy converters were selected.
Keywords:
Wave energy converter, Maximum wave height, Significant wave height, Average wave height, Peak wave period, Rayleigh distribution1. Introduction
The development of renewable energy has been rapidly progressing owing to the depletion of fossil energy and the increased emission of greenhouse gases from the use of fossil energy. Among them, energy sources that can be obtained from the ocean are varied and abundant, and interest in these sources is continuously increasing. Examples of marine renewable energy include wave power generation that produces electrical energy using waves, tidal power generation that produces electrical energy using variation of the sea level, and current power generation using ocean currents. Such marine energy technology development is actively progressing. The tidal power plant built on Lake Sihwa on the west coast of Korea is the world's largest tidal power plant, with a facility capacity of 254 MW. Furthermore, the first tidal power plant in Asia, the Uldolmok power plant, is currently in trial operation, and its development is ongoing for commercialization [1]. For domestic wave power generation technology, a 500 kW wave power plant was built and operated in Yongsu-ri, Jeju, in 2016.
However, most technologies that can obtain energy from the ocean are still difficult to commercialize. First, a large initial cost is required to build the relevant facilities, and the design requirements of the generator vary according to the characteristics of the installation area. Several efforts have been made to reduce the design cost required for tidal and wave power generation [2]. According to the operating principle of wave power generation, technology development and demonstration of wave energy converters (WECs), such as 'experimental study of shape parameter of land-based OWC wave energy converter' [3], numerical simulations and experiments for shape and power efficiency calculation of OWC wave power generators applied to floating light beacons [4], preliminary studies on the optimum shape of caisson structure embedding wave power generation [5], the performance of wave power generation using caisson-type breakwater [6], and the effects of the structural geometry on the energy-harvesting efficiency of multistage overtopping wave energy converters [7], have been actively conducted.
In European countries, various types of wave power system technology developments and actual sea area empirical research are in progress. Similarly, in Korea, investigations have been conducted on the applicability of wave power generators in domestic coastal seas. The wave energy density of the Korean coastal waters was calculated based on wave data for 24 years (1979–2002). It was found that approximately 3 kW/m of subsistence wave energy was distributed in the coastal waters of Korea [8]. With the support of the Korea Energy Technology Evaluation and Planning, technology development for a 1 MW class floating body arrayed wave energy converter that can respond to wave changes is in progress in the waters near Chagwido, west of Jeju Island [9]. In addition, to develop a 2.5 GW class offshore wind farm in the southern part of the West Sea of Korea, wind and wave data were measured in the waters of Wido-myeon, Jellabuk-do [10]. Based on the data measured for three years using a hydraulic wave meter in the water area in front of the Hupo port on the east coast of Gyeongsangbuk-do, a study was conducted to improve the efficiency even in a sea area with weak and unevenly distributed wave power by developing and optimally designing a resonance-type wave power generator system [11]. However, previous studies focused only the characteristics of a single sea area or a specific sea area. Although Jeong [12] conducted a review of the characteristics of the entire sea area in Korea, the sea observation data used were old, comprising wave output data from 1979 to 2002, and the reliability of the data observed from several buoys during this period has been questioned [13]. In addition, in a study of the Korean coastal applicability of wave-induced swirl water chambers, it is necessary to apply them to more diverse environments, which indicates that there is insufficient data on all coastal waters in Korea [14].
This paper presents a preliminary study of the optimal model design of overtopping wave energy converters based on moving particle simulation (MPS) and analysis of the characteristics of the domestic sea area to select the optimal facility location for the overtopping wave energy converters. For the selection of the sea area, several sea areas representing the West Sea, the South Sea, and the East Sea of Korea were selected among the sea areas where the buoys were installed. Data from 2011 to 2020 from ocean data buoys installed by the Korea Meteorological Administration (KMA) were used to understand the characteristics of the sea area. The frequencies according to the maximum wave height (Hmax), significant wave height (Hs), average wave height (Havg), and peak period (Tp) for each selected sea area were investigated. Through this, by comparing the characteristics of each sea area, the characteristics of the domestic coastal sea for operating overtopping wave energy converters can be utilized in future designs.
2. Wave Observation
2.1 Selection of observation data
This study analyzed wave data provided by ocean data buoys in each sea area to consider the characteristics of the domestic coastal seas (West Sea, South Sea, and East Sea) [15]. The selected ocean data buoys are summarized in Table 1. Cases 1–21 represent coastal buoys located closer to the shore than ocean meteorological buoys, and Cases 22–33 represent ocean meteorological buoys. The location information on the latitude and longitude of the buoys installed in the sea was compiled based on information provided by the Korea Hydrographic and Oceanographic Agency (KHOA). Furthermore, to classify the characteristics of the sea area by buoy location, the West Sea (W), South Sea (S), and East Sea (E) are classified and listed in Table 1 based on the standards defined by the KHOA. The observation period of the data measured from the selected buoy was at least six years and up to 10 years. According to Cho et al. [16], if basic wave information is used for more than one year, the wave estimation error is significantly reduced, and if data are used for approximately three years, the average wave height estimation error is considered to be approximately 10%. Therefore, because wave characteristics analysis for each sea area using longer-term data was conducted, the sea area characteristics to be described later can be regarded as data that can represent wave information of the sea area.
The ocean meteorological observation buoy and ocean data buoy data provided by the meteorological data open portal of the KMA are provided at intervals of 1 h, and 1 d for each measurement point. Daily interval data have been provided since 1998; however, there is a disadvantage because the amount of data lost or not measured at each measurement point is large. Minute interval data have been provided since March 2016; therefore, the amount of data is relatively small. In the case of time interval data, since 2011, long-term data of approximately 10 years can be secured, and data loss is relatively small. In this study, data were collected at 1-hour intervals and analyzed.
To explain the provided data, they were observed at a wave height and period of 0.1 m and 0.1 s, respectively, and spectrum analysis was performed on the significant wave height and wave period. Additionally, 1,024 data points were sampled at 1 Hz. The significant wave height and wave period were calculated by spectral analysis of sea level displacement as follows, and data were produced and collected every hour.
| (1) |
where f is the frequency and E(f) is the dispersion density for each frequency obtained from the spectrum analysis of the displacement of the sea level.
2.2 Analysis of observation data
Prior to the analysis of the observation data, the wave data were provided in the form of time series data with an interval of 1 h, such as significant wave heights and peak periods at one time interval. Extreme distributions, such as the significant wave height over a long period, can be described as a trivariate Weibull distribution. In this case, the wave heights of individual waves that can occur within each section spaced by one hour should be described with a short-term probability model, such as the Rayleigh distribution [17]. When the frequencies of the component waves constituting an irregular wave are clustered near a specific value, such a wave is referred a narrow-banded wave, and most wind waves and swells belong to narrow-band waves [18]. In the case of an irregular wave belonging to a narrowband wave, it is well known that the distribution of the wave amplitude follows the Rayleigh distribution if the distribution of the waveform follows the Gaussian distribution. In the narrowband sea, the envelope changes slowly, the distribution of individual wave heights follows the Rayleigh distribution, and the definition of the Rayleigh distribution is given by Equation (2) below [19].
| (2) |
where p is the probability density per meter or the percentage of the number of times that any particular wave height (Hi) is 0<p<1. If p is 0, Hi never occurs; if p is 1, Hi occurs every time. In addition, is the mean of the squares of the wave heights defined as follows(variance).
| (3) |
where f(Hi) represents the number of occurrences of Hi.
As mentioned previously, the data provided by the KMA are in the form of a time series with a time interval of 1 h, containing information such as wave height, wave period, and wave direction. Although it is different for each observation point, the probability density function distribution was confirmed by arranging the frequency of occurrence for each wave height average value according to the 0.1 m wave height range for 40,000–80,000 data points based on data from six to 10 years. By applying Equation (2), the Rayleigh distribution was confirmed and compared. Further, through a case study on a total of 33 observation points, the probability information of the wave height and wave period of 1 year, 10 years, 50 years, and 100 years was calculated, which is meaningful in terms of engineering aspects. This was intended to be reflected in future studies on the optimal shape of overtopping wave energy converters.
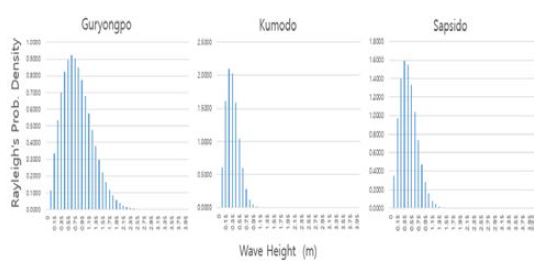
Figure 1 shows the Rayleigh distribution of the significant wave height for each sea area in the observed data using Equation (2). Evidently, the Rayleigh distribution of significant wave heights clearly matches the characteristics of the average significant wave height (wave height 0.5–2.0 m) in the Korean sea area. Further, the distribution of significant wave heights is different for each observation location.
3. Analysis Results
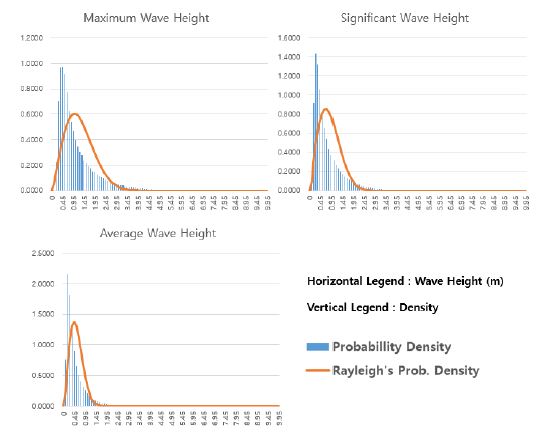
The analysis results of the observation data of the 33 types of ocean data buoys were divided into the West Sea, South Sea, and East Sea. To analyze the characteristic trend of each sea area, case study results for the two cases are presented for each sea area. Figure 2 shows the probability density function (PDF) and Rayleigh distribution of the 10-year maximum, significant, and average wave height based on the wave measurement data of the coastal buoys at Jeju Port as an example. The horizontal axis of each graph represents the wave heights from 0 to 10 m at intervals of 0.1 m, and the vertical axis represents the probability density for each wave height of the data. Further, the blue histogram of the resulting values represents the PDF and the orange distribution curve represents the Rayleigh distribution.
3.1 Results by sea area
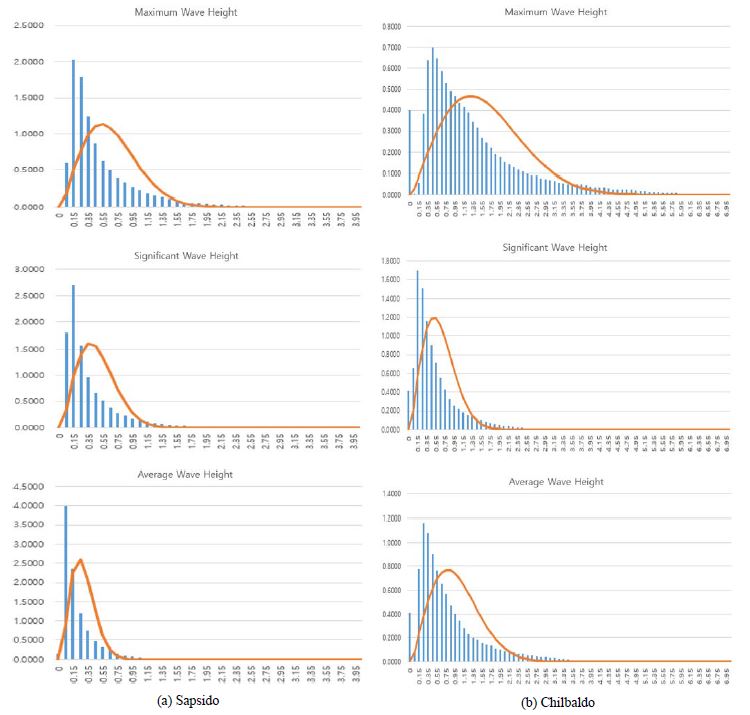
Figure 3 shows the results of the analysis of the marine data of Sapsido and Chilbaldo in the coastal sea close to the shoreline of the West Sea and the coastal seas of the West Sea, respectively. Table 2 shows the probability information about the wave heights and periods of 1, 10, 50, and 100 years for all the data measured from the ocean data buoys located in the West Sea.
Figure 4 shows the results of the analysis of sea data of Yeongok and Seogwipo in the coastal sea close to the shoreline of the South Sea and the coastal seas of the South Sea, respectively. Table 3 summarizes the probability information of the wave heights and periods of 1, 10, 50, and 100 years for all data measured from the ocean data buoys located in the South Sea.
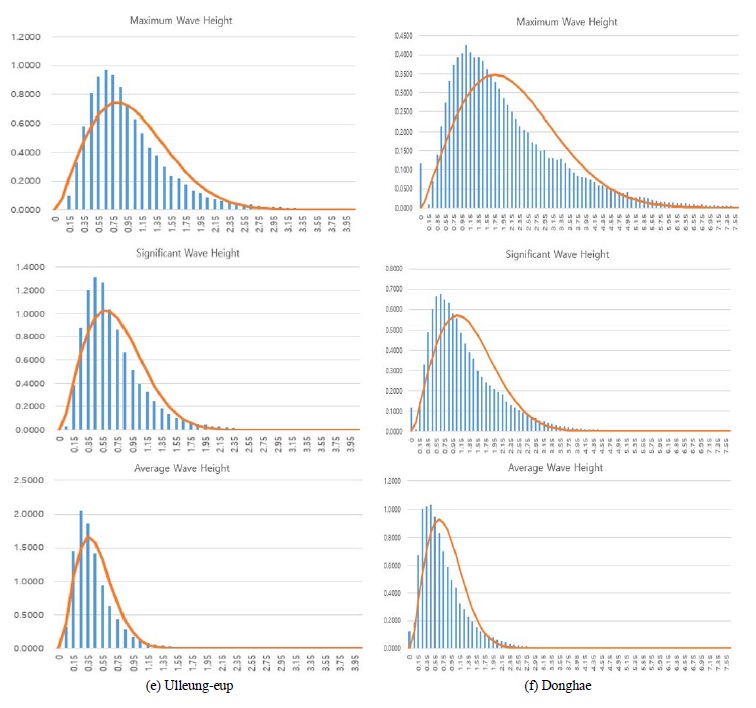
Figure 5 shows the results of the analysis of sea data of Ulleung-eup and Donghae in the coastal sea close to the shoreline of the East Sea, and the coastal seas of the East Sea, respectively. Table 4 summarizes the probability information of the wav heights and periods of 1, 10, 50, and 100 years for all data measured from the ocean data buoys located in the East Sea.
3.2 Review of the results
The optimal selection conditions of the sea area for the overtopping wave energy converters design were set as follows.
- - A sea area showing a narrowband pattern wherein the Rayleigh distribution patterns of Hmax, Hs, and Havg are clustered near a certain range.
- - In the case of a similar Rayleigh distribution, the sea area with a high wave height distribution range, which is the horizontal axis of the Rayleigh distribution
The selection conditions were set as described previously because the design requirements for wave energy converters should consider the characteristics of the sea area. Specifically, the wave power generator is installed considering the wave height of the sea area where the wave power generator will be operated. At this time, the probability of having a constant wave height is reduced in the sea area, where the wave height distribution has a wide distribution in the form of a broad band, such that the energy of the wave cannot be used properly. If the Rayleigh distribution of the wave height shows a narrow-band distribution, this is the case with the highest probability that a wave with a similar wave height will consistently affect the wave energy converter. Therefore, we preferentially selected the Rayleigh distribution with respect to the wave height to represent a narrow band form clustered around a certain range. Next, because the energy density of a wave is proportional to the square of the wave height, the sea area with a high wave height, which is the value of the distribution range, was selected as the optimal location for the wave generator design among sea areas with a narrow Rayleigh distribution range. The optimal location selection results among the 33 case studies are listed in Table 5.
4. Conclusion
In this study, to derive the optimal shape of overtopping wave energy converters, time series data of the maximum wave height, significant wave height, average wave height with 1-hour intervals, and peak period measured from ocean data buoys installed in coastal and offshore seas in Korea were used. The wave height of each wave was expressed as a short-term probability model using the Rayleigh distribution by collecting observation data for 10 years measured at intervals of one hour. Subsequently, a case study was performed and analyzed for a total of 33 sea area locations.
The criteria for selecting the optimal location for the operation of the wave energy converter to effectively reflect the wave characteristics of the sea area were as follows.
- - A sea area showing a narrowband pattern wherein the Rayleigh distribution patterns of Hmax, Hs, and Havg are clustered near a certain range.
In the case of a similar Rayleigh distribution, the sea area with a high wave height distribution range, which is the horizontal axis of the Rayleigh distribution.
As a result of analysis by sea area, the sea areas near Jeju Port, Yeongok, and Hyeoram satisfied the selection criteria. In the case of relatively distant sea areas, it was confirmed that the sea areas near Ulleungdo, Donghae, and Seogwipo satisfy the selection criteria. However, as a result of analyzing the data of the sea area located in the West Sea, it was far from the optimal location selection criteria for wave energy converter operation. This is considered to be the reason why the distribution of wave heights is not constant because wave deformation owing to the shape of the coastline, islands, and currents occurs more frequently in the West Sea than in other sea areas. Among the selected sea areas, the sea area where typhoons are frequent is a major factor in increasing the initial investment cost. This is because although it has a very high wave energy density region during a typhoon, it cannot be used for commercial power and can also require strengthening the design requirements of facilities. In addition, the additional cost of electricity transmission can be reduced when it is installed in a sea area not far from the electricity demand point. By adding additional considerations to the results of the analysis of the sea area, a location with reasonable initial investment cost, operating cost, and energy production efficiency will be selected and reflected in the design to derive the optimal shape of the overtopping wave energy converters in the future.
Acknowledgments
This work was supported by National R&D Program through the National Research Foundation of Korea (NRF) funded by the Korea government (Ministry of Science and ICT) (No. 2021R1I1A3057230).
Author Contributions
Conceptualization, G. Kim, S. An and J. Lee; Methodology, G. Kim, S. An, J. Lee; Software, S. An; Validation, G. Kim, S. An and J. Lee; Formal Analysis, G. Kim, S. An; Investigation, G. Kim, S. An; Resources, G. Kim; Data Curation, G. Kim, S. An; Writing—Original Draft Preparation, G. Kim; Writing—Review & Editing, S. An, J. Lee; Visualization, G. Kim, S. An; Supervision, J. Lee; Project Administration, J. Lee; Funding Acquisition, J. Lee.
References
-
M. -K. Ko, J. -W Choi, J. -H. Yi, and W. -M. Jeong, “Acoustic characteristics of underwater noise from Uldolmok tidal current pilot power plant,” Journal of the Acoustical Society of Korea, vol. 31, no. 8, pp. 523-531, 2012 (in Korean).
[https://doi.org/10.7776/ASK.2012.31.8.523]

- A. Garanovic, Offshore-Energy, https://www.offshore-energy.biz/eu-targets-40-gw-of-ocean-energy-and-other-emerging-technologies-by-2050, /, Accessed November 11, 2021.
-
W. -C. Koo, J. -S. Kwon, J. -D. Kim, S. -J. Kim, M. -W. Kim, and M. -K. Choi, “Experimental study of shape parameter of land-based OWC wave energy converter,” Journal of Ocean Engineering and Technology, vol. 26, no. 3, pp. 33-38, 2012 (in Korean).
[https://doi.org/10.5574/KSOE.2012.26.3.033]

- K. -P. Son, Numerical Simulation and Experiment for Shape and Power Efficiency Calculation of OWC Wave Power Generator applied to Floating Light Beacon, Ph. D. Dissertation, Department of Civil & Environmental Engineering, Wonkwang University, Republic of Korea, 2019.
- J.-S. Lee, Preliminary study for optimum shape of caisson structure embedding wave power generation, M.Sc. Dissertation, Department of Ocean Engineering, Pukyong National University, Republic of Korea, 2009.
- K.-Y. Bae, The performance of wave power generation using caisson type breakwater, M.Sc. Dissertation, Department of Ocean Engineering, Kwandong University, Republic of Korea, 2009.
-
J. Sirirat and B. -S. Hyun, “Effects of structure geometry on energy harvesting efficiency of multi-stage overtopping wave energy converters,” Journal of the Korean Society for Marine Environment & Energy, vol. 20, no. 3, pp. 136-144, 2017.
[https://doi.org/10.7846/JKOSMEE.2017.20.3.136]

- M. -S. Song, D. -Y. Kim, M. Kim, K. -Y. Hong, and K. -C. Jun, “Analysis of wave energy density for Korean coastal sea area based on long-term simulated wave data,” Journal of the Korean Society for Marine Environmental Engineering, vol. 7, no. 3, pp. 152-157, 2004 (in Korean).
-
D. -E. Kim, K. -P. Sunny, and Y. -H. Bae, “Numerical study on linear behavior of arrayed pitch motion wave energy converters,” Journal of the Korean Society for Marine Environment & Energy, vol. 23, no. 4, pp. 269-276, 2020 (in Korean).
[https://doi.org/10.7846/JKOSMEE.2020.23.4.269]

-
D. -H. Ko, S. -T. Jeong, H. -Y. Cho, and K. -S. Kang, “Comparative analysis on the design conditions for offshore wind power structures in the coastal sea of Korea,” Journal of Korean Society of Coastal and Ocean Engineers, vol. 26, no. 1, pp. 25-32, 2014 (in Korean).
[https://doi.org/10.9765/KSCOE.2014.26.1.25]

-
H. -M. Kweon, H. -Y. Cho, and W. -M. Jeong, “Wave analysis and spectrum estimation for the optimal design of the wave energy converter in the Hupo coastal sea,” Journal of Korean Society of Coastal and Ocean Engineers, vol. 25, no. 3, pp. 147-153, 2013 (in Korean).
[https://doi.org/10.9765/KSCOE.2013.25.3.147]

- T. J. Shin, J. -D. Jeong, and H. -Y. Cho, “Characteristics on the extreme value distributions of deepwater design wave heights off the Korean coast,” Journal of Korean Society of Coastal and Ocean Engineers, vol. 16, no. 3, pp. 130-141, 2004 (in Korean).
- B. -H. Choi and K. -O. Kim, “Status of wave observations at Korean coastal waters,” Proceedings of the Korean Society of Coastal and Ocean Engineers, vol. 18, no. 10, pp. 93-96, 2009.
-
J. -K. Choi and H. -T. Kim, “Numerical investigation on the applicability of wave-induced swirl water chamber for wave power generation in coastal water of Korea,” Journal of Ocean Engineering and Technology, vol. 27, no. 6, pp. 32-42, 2013 (in Korean).
[https://doi.org/10.5574/KSOE.2013.27.6.032]

- Korea Meteorological Administration (KMA), Open Data, https://data.kma.go.kr/data/sea/select-BuoyRltmList.do?pgmNo=52, , Accessed 1 August, 2021.
-
H. -Y. Cho, W. -M. Jeong, and K. -C. Jun, “Relationship analysis on the monitoring period and parameter estimation error of the coastal wave climate data,” Journal of Korean Society of Coastal and Ocean Engineers, vol. 25, no. 1, pp. 34-39, 2013 (in Korean).
[https://doi.org/10.9765/KSCOE.2013.25.1.34]

-
G. -Z. Forristall, “How should we combine long and short term wave height distributions?,” Proceedings of ASME2008 27th International Conference on Offshore Mechanics and Arctic Engineering, 2009.
[https://doi.org/10.1115/OMAE2008-58012]

- D. -E. Ko and B. -S. Jang, Ship and Offshore Structural Mechanics, Seoul, Korea: Textbooks Publisher, 2017 (in Korean).
- D. -Y. Kim, “On individual wave height distribution of ocean waves,” Proceedings of the Korea Committee for Ocean Resources and Engineering Conference, the Korean Society of Ocean Engineers, pp. 367-372, 2006 (in Korean).