시간 지연을 고려한 해상 크레인의 상하 동요 보상 시스템의 강인 제어

2.1 동역학 모델의 가정과 좌표계 설정

해상 크레인의 상하동요 보상 시스템은 해상 크레인과 유압 구동식 윈치, 탄성을 가진 로프, 그리고 로프의 끝단에 위치한 중량물로 구성된다[2]. 해상 크레인은 강체 시스템으로 간주되며, 유압 구동식 윈치의 동역학식은 1차 시스템으로 정의한다. 시스템의 상하동요 움직임만을 예측ᐧ제어하기 때문에, 중량물의 상하 운동만을 고려한 1차원 시스템으로 가정한다. 같은 이유로 선박의 동역학에서는 수평 방향 성분에 영향을 미치는 외란은 고려하지 않는다. 여기서의 상하동요 보상 시스템은 ROV(Remotely operated underwater vehicle, ROV)와 같은 중량물이 로프 끝단에 매달려서 깊은 수심에 위치하는 경우, 그 위치를 유지하는 것을 목표로 한다.

시스템의 좌표는 해수면에서 수직 아래 방향을 양의 방향으로 정하며, 중량물의 위치 제어가 목적이므로 중량물의 위치 z를 변수로 잡는다. 중량물의 위치는 로프의 길이 함수 l과 탄성력에 의한 로프의 길이 변화량 ∆l, 그리고 외란에 따른 크레인의 수직 운동이 중량물의 위치 변화에 미치는 영향력을 변수로 하는 w를 모두 고려하여 정의한다.

문제의 상황을 단순화하기 위해, 윈치와 로프는 같은 축 위에 함께 있다고 가정한다. 이 가정은 기준점의 위치 변화만 고려하게 되므로 동역학 모델의 성격을 해치지 않는다. 여기서 로프의 길이는 윈치의 윈치 각도에 종속된 변수이며 다음과 같이 표현된다.

l₀는 로프의 초기 길이값이며, r은 윈치의 반지름, 그리고 ψ(t)는 윈치의 각변위에 해당한다.

로프는 탄성을 가지며, 탄성계수는 다음과 같다.

여기서 E 는 로프의 영률(Young’s modulus)이며 A는 로프의 단면적에 해당한다.

중량물의 위치와 관련된 동역학을 구성하기 위해서는 로프의 길이 변화량을 정적(Static), 동적(Dynamic) 변화량으로 각각 나누어 살펴보아야 한다.

2.2 동역학 모델의 역학 관계식

로프 길이의 정적 변화량은 정적 평형 상태에서의 힘의 방정식으로부터 얻을 수 있다. 평형 상태에서의 힘의 방정식은 다음과 같다.

F_g, F_cr,s 그리고 F_b는 각각 중력, 로프 길이의 정적 변화에 따른 탄성력, 그리고 부력에 해당한다. 각각의 힘들은 다음과 같다.

여기서 g는 중력 상수, m_p는 중량물의 질량, m_l,r은 로프의 단위 길이당 질량, ρ_w는 물의 밀도, V는 중량물의 부피, 그리고 l_w는 물에 잠긴 로프의 길이를 나타낸다.

동역학 모델에서 중량물의 질량은 다음과 같다.

A₃₃은 수중에서 수직 방향으로 운동하는 물체가 받는 수직 방향으로의 부가질량(Added mass)에 해당한다.

로프 길이의 동적 변화는 뉴턴의 운동방정식을 적용함으로써 얻는다.

$$ \stackrel{\text{̈}}{z}$$는 중량물의 가속도 항이며, F_cr,d, F_dr, 그리고 F_d는 각각 로프 길이의 동적 변화에 따른 탄성력(Dynamic spring force), 감쇠력(Rope’s damping force), 그리고 중량물에 작용하는 항력(Hydrodynamic drag force)을 나타낸다. 각각의 힘들은 다음과 같다.

C_ds는 중량물의 항력 계수(Drag coefficient), A_p는 중량물의 수직 단면적(payload’s nominal cross-sectional area in the vertical direction), $$ {\stackrel{\text{̇}}{z}}_w$$는 중량물 주변 유체 입자의 속도를 표현한다. 본 논문에서는 깊은 수심에 있는 중량물을 두고 동역학 모델을 세우고 있으므로, $$ {\stackrel{\text{̇}}{z}}_w$$는 무시할 만큼 작다고 가정할 수 있다.

상하동요 보상 시스템에서 제어 입력은 유압 구동식 윈치 시스템에 포함되며, 윈치 동역학 식은 다음과 같다.

윈치의 각가속도항 $$ \stackrel{\text{̈}}{\psi }$$은 상하동요 보상 시스템에서 직접 제어하는 값이며, T_w는 윈치의 시간 상수, u_w는 입력 전압에 해당한다. K_v,w는 u_w의 유량 변화율에 대한 비례 상수이며, i_w는 전송률, 그리고 V_mot,w는 유압식 모터의 부피에 해당한다.

3.1 PD 제어

본 연구에서 사용된 능동형 상하동요 보상 시스템 제어는 중량물의 위치를 실시간으로 계측하여 크레인 끝단의 상하 운동을 계산한다. 중량물이 제 위치를 유지하도록 추종하는 목표 변위와 속도를 각각 정하면, 현재 변위와 속도와의 차이로부터 그 오차를 정의할 수 있다. 이렇게 정의된 오차로부터 PD 제어를 적용해 중량물의 위치가 외란으로부터 유지되도록 한다. 수중 운동체의 경우 감쇠운동을 고려하기 때문에, PD 제어를 활용하여 적절한 자세 제어를 유지하도록 한다. 유압 구동식 윈치의 동역학은 간단한 이차 미분방정식이므로, 이를 풀면 윈치의 각변위항과 제어 입력간에 관계식을 식 (15)와 같이 구할 수 있다.

제어 입력과 출력간 관계식은 선형화를 통해 식 (16)과 같이 얻어지며, 이를 통해 PD 제어의 입력을 구한다.

3.2 슬라이딩 모드 제어

앞 절에서 정립한 동역학 모델을 바탕으로 상태 공간 방정식(State space equation)으로 변환한다. 우선 상태 벡터는 식 (17)과 같이 정의된다.

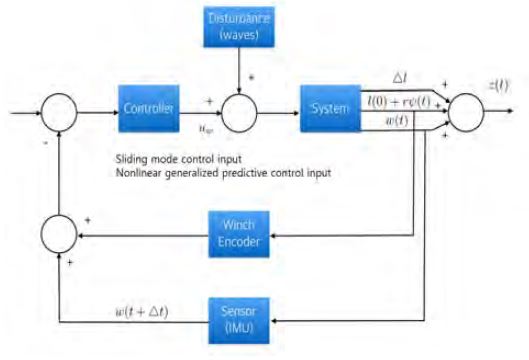
이에 따른 AHC (Active Heave Compensation) 시스템의 동역학적 특성을 갖는 상태 공간 방정식은 식 (18)과 같다. f(x)는 시스템의 동역학적 특성을 모두 담고 있는 행렬이며, g는 제어 입력에 대한 상수곱 행렬로서, 윈치의 특성을 반영한다. d(t)는 시스템에 입력되는 외란에 해당하며, C 는 시스템 전체 출력값을 정립하기 위해 필요로 되는 행렬이다[3].

외란 및 각종 변수들의 불확실성이 시스템에 큰 부분을 차지하고 있는 경우, 강인한 제어기(Robust controller)를 활용하는 것이 적합하다. 특히 본 논문에서 다루고 있는 AHC 시스템은 비선형 동역학적 특성을 가진 시스템이며, 외란에 따른 불확실성을 동시에 포함하고 있으므로, 슬라이딩 모드 제어기 (Sliding mode controller, SMC)를 활용한다. SMC는 파라미터의 불확실성 또는 외란에 강인한 제어기이며, 동시에 비선형 시스템에도 쉽게 적용할 수 있는 장점을 갖고 있다[4][5]. 따라서 본 논문에서의 AHC 시스템에 SMC를 적용하기 위해 슬라이딩 평면 s를 y와 $$ \stackrel{\text{̇}}{y}$$의 추종 위치 및 속력과의 오차로 정의하면 다음의 식 (19)와 같고

Lyapunov stability를 만족할 때 슬라이딩 평면은 0으로 수렴하며, AHC 시스템의 제어 목적이 달성되는 상황으로 들어가게 된다. 추종 위치 및 속력과의 오차 값을 각각 $$ \stackrel{\text{̃}}{y}$$, $$ \stackrel{\text{̇}}{\stackrel{\text{̃}}{y}}$$라고 하면,

식 (18)과 식 (21)로부터 오차관계식은 다음과 같이 성립된다.

$$ \stackrel{\text{̇}}{s}$$=0이 성립하기 위해 최적의 제어 입력을 $$ \widehat{u}$$(Equivalent control)이라 하면, $$ \widehat{u}$$는 다음과 같다.

이에 따른 SMC의 제어 입력은 다음과 같다.

식 (25)는 Lyapunov stability를 만족하기 위한 슬라이딩 조건에 해당한다. 불확실성을 포함하는 파라미터의 제한 조건은 식 (26)와 같다.

3.3 비선형 일반 예측 제어

외란 및 각종 변수들이 존재하는 비선형 동역학 시스템에서, 비선형 예측 제어기를 활용하면 추종하는 위치로 도달하도록 효과적으로 할 수 있다[6][7]. 다음의 식 (28)은 제어 입력을 나타낸다.

여기서 ρ는 시스템의 상대 차수(Relative degree)이며, r(t)는 추종하는 위치 함수에 해당한다. 행렬 K, M은 r(t)의 테일러 전개(Taylor expansion)와 예측 시간을 고려한 계산된 예측값을 포함하는 행렬로, 식 (29)와 같다.

식 (28)은 비선형 시스템에 대한 일반적인 예측 제어로써 활용됨과 동시에, 다른 제어기와 함께 사용될 수 있다. 강인제어기인 SMC(u_S)와 더불어 쓰일 경우 제어 입력은 다음의 식 (30)과 같이 표현된다.

이와 같은 제어기 설계를 통해, 외란에 강인하며, 시간에 따라 변하는 제어목표물의 위치 예측 제어를 동시에 수행할 수 있는 이점을 가질 수 있다.

4.1 시뮬레이션

동역학식으로부터 시스템 구현 및 제어를 위해 블록 모델을 구성했으며, 실제 운용되는 해상 크레인의 작업 환경과 유사한 시스템 구현을 위해, 시뮬레이션에서 사용된 제원 및 특성은 Table 1과 같다[8].

Table 1:

Parameters used for the simulation in analyzing numerically

시스템의 블록 선도는 Figure 1에 도시하였다.

Figure 1:

The block diagram for active heaving compensation system

시뮬레이션은 Simulink를 활용한 수치적 시뮬레이션을 설계했으며, 계산 시간은 100초, 규칙적인 외란(w(t)=0.5sin5t)이 입력되는 시스템으로 시뮬레이션을 수행했다.

4.2 시뮬레이션 결과

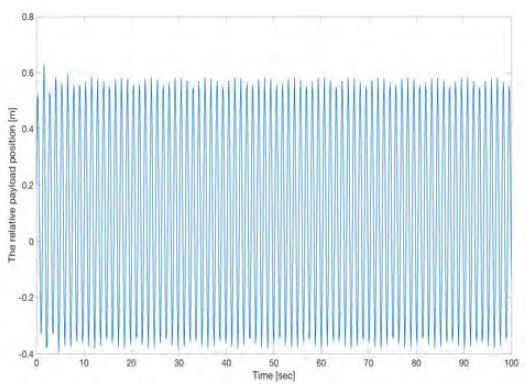
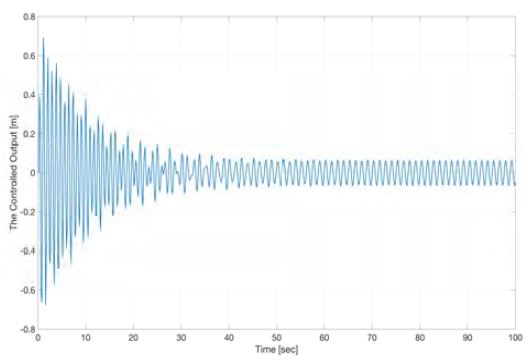
시뮬레이션을 수행한 결과, 시스템의 동역학적 특성 즉, 중량물이 외란을 받는 경우 상하동요 변위값 그래프는 Figure 2와 같이 나타났다. 중량물이 초기 위치를 기준점으로 상하로 진동하는 움직임을 보여주는 그래프로 표현했으며, 진동하는 최대 변위의 크기는 0.58m에 해당한다.

Figure 2:

The relative motion of payload in heave compensation system

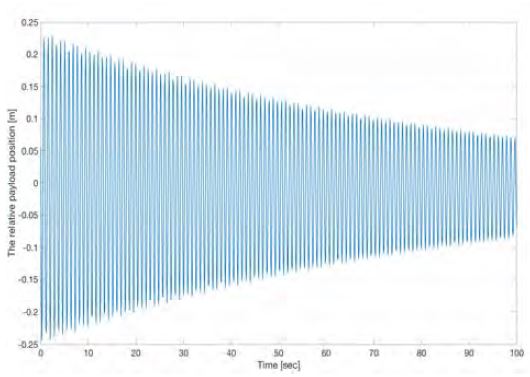
Figure 3에서는 PD제어를 이용해 중량물의 위치를 제어한 결과를 도시했다. 비레이득(K_p)은 0.52, 미분이득(K_D)은 0.12, 미분시간(T_D)는 0.05초이며, 제어 입력은 0.1초 간격으로 입력되었다. 제어 결과 최대 변위의 크기가 시간에 따라 줄어드는 것을 확인할 수 있다.

Figure 3:

The relative motion of payload in heave compensation system with PD control

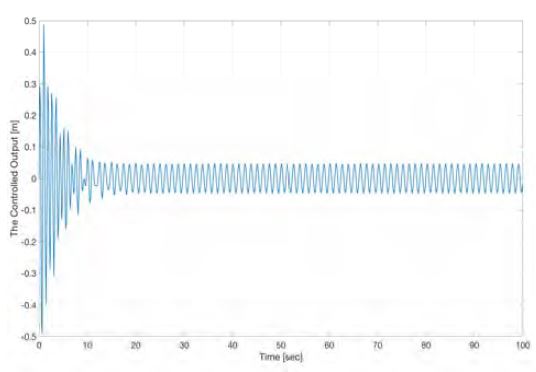
SMC를 적용한 결과를 Figure 4에서 도시하였다. 진동하는 최대 변위는 0.0602m로 감소했음을 확인할 수 있다. 강인제어기로 외란을 효과적으로 상쇄하고 있음을 나타내고 있다.

Figure 4:

The relative motion of payload in heave compensation system with sliding mode control input applied

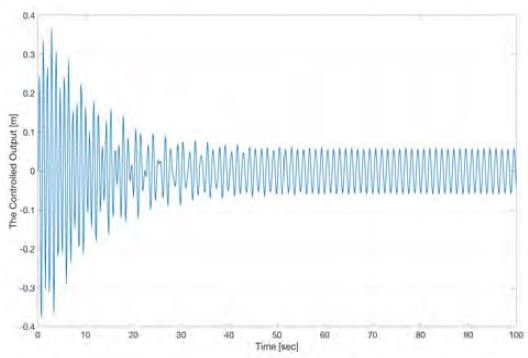
그러나 계측 장비와 입력의 신호 전달에 있어 시스템 전체에는 시간 지연이 있으므로 이를 고려해야 한다. 전체 시스템에서의 시간 지연 (Time delay)이 1s라고 가정하고, SMC만 적용한 것을 Figure 5에 도시하였다. 진폭의 큰 변화는 없으나 실제 시간 지연이 존재하는 경우 추종하는 위치로의 수렴 시간이 길어짐을 확인할 수 있다. SMC와 비선형 일반 예측 제어 입력을 함께 적용한 결과를 Figure 6에서 도시하였다. 진동하는 최대 변위가 0.0572m로 감소되었다. 시뮬레이션 시간상 초기 구간에서 진폭을 줄이는 결과를 보였다.

Figure 5:

The relative motion of payload in heave compensation system with sliding mode control input applied where ,1s time delay existing

Figure 6:

The relative motion of payload in heave compensation system with both sliding mode control input and nonlinear general predictive control input applied where 1s time delay existing