ARMA기반의 데이터 예측기법 및 원격조작시스템에서의 응용

2.1 ARMA모델

ARMA모델은 자기회기(autoregressive)부분과 이동평균(moving average)부가 결합된 형태로 식 (1)과 같은 형태로 구성된다[11].

식 (1)에서와 같이 ARMA모델은 현재의 신호 w_t가 이전에 관측된 p 개의 신호와 q개의 잔차(residual)에 대한 가중합(weighted sum)으로 결정된다. 이때 ϕ_j를 AR계수라 하고 θ_k를 MA계수라 하는데 각각 p와 q의 개수를 가진다. 일반적으로 p개의 AR계수와 q개의 MA계수로 구성된 ARMA모델은 ARMA(p,q)로 표현된다.

ARMA모델은 시계열 데이터 분석에 주로 이용된다[11][12]. 이러한 경우 가장 중요한 이슈로 다음의 두 가지를 들 수 있다. 첫째, 수집된 시계열 데이터를 가장 잘 설명할 수 있는 모델을 결정하는 것(모델 선택 문제)이며, 둘째로는 선택된 모델에 따른 계수들을 추정하는 것(모델 파라미터 추정 문제)이다[11]. 하나의 시계열 자료를 분석하는 경우, 모델 선택 및 파라미터 추정과정은 가장 적절한 모델을 얻기 위해 여러 번의 교정과 검증의 과정을 거치게 된다.

본 논문에서는 햅틱기반의 원격조작시스템에서 네트워크 환경에서 전송되는 햅틱데이터에 대한 예측을 통해 시간지연에 따르는 오차의 보상 목적으로 ARMA모델을 이용한다. 따라서 시계열 데이터는 햅틱장치가 보장하는 최소 1ms의 샘플링 시간에 대한 데이터의 획득이 가능하며, 데이터의 개수 또한 많은 특징이 있다. 따라서 모델선택은 사전에 획득된 데이터 집합으로부터 오프라인(off-line) 상에서 최적의 모델이 되도록 p와 q를 결정한다.

2.2 ARMA모델의 학습 알고리즘

ARMA 모델의 파라미터를 추정하기 위해 식 (1)을 잔차항(residual term)에 관해서 전개하면 다음과 같다.

식 (2)에서 잔차를 β에 관한 함수 형태로 간주한 것은 현재의 잔차가 과거의 잔차로부터 영향을 받기 때문이다. 즉, 현재시간에서의 잔차는 과거의 잔차에 의존되어 있다. 최적의 파라미터 β=(μ,ϕ₁,…,ϕ_p,θ₁,…,θ_q)^T를 추정하기 위해 식 (3)과 같은 목적함수(object function)를 고려하자. 즉, t>p+1의 모든 시간에서 산출되는 오차에 대한 제곱의 합이 최소가 되는 파라미터 벡터가 우리가 구하고자 하는 최적의 파라미터 벡터이다.

식 (3)의 목적함수는 식 (2)를 통해 알 수 있듯이 선형방정식이 아니기 때문에 닫힌해를 구할 수 없다. 수치해석적인 접근방법으로, 식 (3)과 같이 목적함수가 오차제곱의 합으로 정의된 경우 Gauss-Newton기법을 적용할 수 있다. 이를 위해서, 우선 파라미터 벡터 β에 대한 초기값을 β₀=(μ⁽⁰⁾,ϕ₁⁽⁰⁾,…,ϕ_p⁽⁰⁾,θ₁⁽⁰⁾,…θ_q⁽⁰⁾)^T라 하고, 오차함수 α_t(β)를 이 초기값 근방에서 1차 테일러 급수 전개를 통해 선형 근사시키면 다음과 같은 식을 유도할 수 있다.

여기서 z_t($$ \widehat{{\mathit{\beta }}_0}$$)는 오차함수 α_t(β)의 자코비안을 나타내며 식 (5)와 같이 정의된다.

다음으로, 선형 근사된 오차함수를 식 (3)에 대입하여 새로운 손실함수(loss function)를 정의하자. 우리가 구하고자 하는 최적의 β는 식 (6)으로 표현되는 손실을 최소로 하여야 한다.

이제, 식 (6)의 α_t($$ \widehat{{\beta }_0}$$)와 zt($$ \widehat{{\beta }_0}$$)는 상수로 구성된 벡터가 되므로, 식 (6)을 최소로 하는 β를 해석적으로 결정할 수 있다. β-$$ \widehat{{\mathit{\beta }}_0}$$ 관한 닫힌해는 다음과 같이 유도된다.

즉, 초기값 $$ \widehat{{\mathit{\beta }}_0}$$가 주어졌을 때, $$ {\widehat{\beta }}_{\left(1\right)}$$은 식 (8)과 같이 간단히 구할 수 있다.

여기서 ∇($$ \widehat{\beta }$$₀)는 식 (7)의 우변 항을 나타낸다. 알고리즘의 구현을 위해 식 (8)을 일반화하여 재귀적 형태로 기술하면 다음과 같다.

식 (5)의 자코비안 z_t($$ \widehat{{\mathit{\beta }}_0}$$)를 구성하는 각각의 요소들(상수항, AR항, MA항)은 오차함수에 대한 편미분을 취하여 유도할 수 있는데, 이는 식 (10) - 식 (12)와 같다.

이들은 재귀적인 형태로 표현 가능한데, 본 연구에서는 식 (10) - 식 (12)를 구하여 자코비안을 구성하기 위해 식 (13)과같은 재귀적 알고리즘을 통해 파라미터를 추정한다.

최종적으로 주어진 시계열 데이터에 대하여 ARMA(p,q)모델의 파라미터 학습을 위한 알고리즘은 Algorithm 1과 같이 정리된다. 알고리즘은 매 스텝마다 세 단계의 계산과정을 거친다. 첫째, 현재 추정된 파라미터로 구성된 ARMA모델에 대하여 모든 시계열 데이터에 대한 잔차를 구한다(line 4). 둘째, 이들 잔차들과 시계열 데이터를 이용하여 자코비안을 구한다(line 5-7). 이렇게 잔차와 자코비안이 구성되면, 마지막으로 가우스-뉴튼 기법을 통해서 파라미터 벡터를 업데이트 한다(line 10). 이러한 과정이 반복되면서 파라미터 벡터에 대한 정지조건이 만족되면 알고리즘은 종료된다.

Algorithm 1:

Learning algorithm for model parameters

2.3 예측 알고리즘

ARMA(p,q) 모델의 파라미터가 알고 있을 경우 기존의 신호들을 이 모델에 적용하면 n-스텝 (n>0) 후의 신호들의 예측이 가능하다. $$ {\widehat{w}}_{t+n}$$을 시간 t에서의 수집된 신호정보 F_t={w_t,w_t-1,w_t-2…}를 이용하여 n-스텝 후의 신호에 대한 예측치(prediction value)라 하자. 또한 $$ {\widehat{a}}_{t+n}$$을 시간 t에서 F_t에 기반하여 n-스텝 후의 잔차에 대한 추정치라 하자. 사실상 $$ {\widehat{w}}_{t+n}$$는 시간 t에서 정보 F_t가 주어졌을 경우 t+n시간에서의 신호에 대한 조건부 기대치(conditional expectation)로 간주되며 E [w_t+n|F_t]로 표현될 수 있다. 시간 t에서 n-스텝 후의 예측치는 식 (1)을 확장한 후 양변에 조건부 기대치를 적용하여 식 (14)와 같이 정리될 수 있다.

여기서 구간 1<m≤t의 경우, 이미 관측된 정보로부터 이미 신호의 값을 알고 있으므로 $$ {\widehat{w}}_m$$ = w_m 라 하자. 시간 t+n 에서 잔차의 추정치는 식 (1)을 잔차에 관한 식으로 정리한 후 조건부 기대치를 적용하여 식 (15)와 같은 정리될 수 있다.

본 논문에서는 m<t인 경우 $$ {\widehat{a}}_m$$=0으로 설정한다. 그러나 예측구간 t≤m≤t+n에서는 $$ {\widehat{a}}_m$$은 식 (15)를 통해 재귀적(recursive)으로 추정될 수 있다. 본 논문에서는 식 (14) - 식 (15)를 기반으로 데이터 예측 알고리즘을 구현하였다.

3.1 실험방법

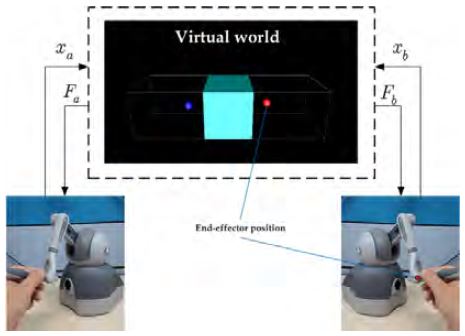
제안된 방법의 유효성을 검증하기 위하여, 본 연구에서는 Figure 1과 같은 실험환경을 구축하였다. 우선, PC환경에는 OpenGL, OpenHaptic 라이브러리를 기반으로 Visual C++언어를 이용한 프로그램을 통해 가상공간(virtual world)이 구축되었다. 두 대의 햅틱장치는 PC와 연동되어 가상공간을 통해 상호작용이 가능하도록 구현되었다. 본 연구에서 사용된 햅틱장치는 3D Systems의 Geomagic Touch 모델이 이용되었다. 가상공간에서의 정육면체 물체는 박스공간에서 1차원 물리적 운동이 가능하도록 설계되었다. 이로써, Figure 1에서와 같이 사용자가 조작 말단부(end-effector)를 통해 정육면체 물체를 밀게 되면 반력을 느끼면서 물체 또한 이동할 수 있게 된다. 따라서 두 명의 사용자는 각각의 햅틱장치를 통해 물체를 매개체로 물리적인 상호작용이 가능하다.

Figure 1:

Experiment setup

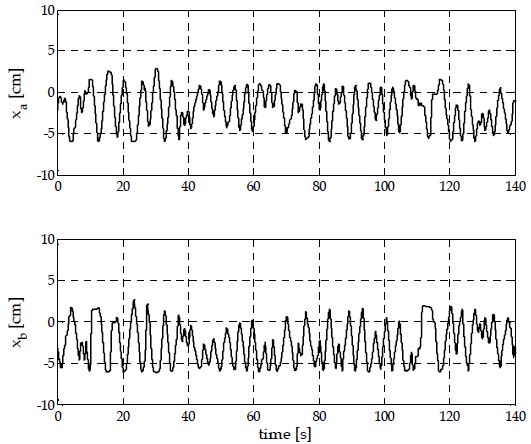
테스트 데이터 집합은 두 명의 사용자가 각각의 햅틱장치를 통해 서로 상호작용을 수행하는 동안 수집되었다. 이 때 데이터는 각각의 장치에 대하여 위치(x_α, x_b) 및 힘(F_α, F_b)에 관한 것으로 160s 동안 매 5ms마다 수집되었다. 성능평가 실험에서 정적 데이터를 배제하기 위하여, 우선 수집된 데이터 중 처음 10s와 마지막 10s에 해당하는 데이터는 제외되었다. 위치 및 힘 데이터 중에서, 본 논문은 연속성이 있는 데이터인 말단부의 위치데이터(x_α, x_b)만을 제안된 방법에 적용시켰다. Figure 2는 실험에 이용된 데이터를 출력한 것이다.

Figure 2:

Test data captured from the experiment environment during haptic interaction

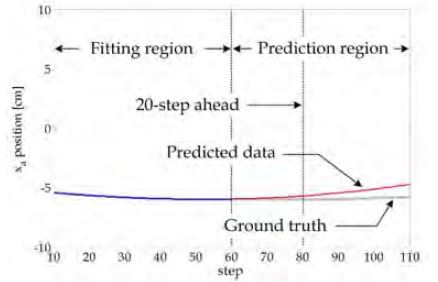
본 논문은 우선 제안된 방법의 예측오차를 기존의 예측방법과 비교하기 위한 실험을 수행하였다. n-차 다항식 회귀(n-order polynomial regression)분석 모델은 미래의 값을 예측하는데 있어 파라미터 학습 및 예측 알고리즘의 구현이 용이한 데이터 예측기법이라 할 수 있다. 이에 본 논문은 제안된 방법의 성능 비교를 위해 회귀분석 모델을 통한 예측결과를 획득하였다. 이 때, 모든 데이터에 대하여 회귀분석을 수행하는 것은 의미가 없으므로, 다음과 같은 절차로 회귀분석을 수행하고 최종적으로 RMS(root mean square)오차를 산출하였다. [단계 1] Figure 3과 같이 데이터의 일부를 회귀분석 구간(50개 샘플데이터)과 예측구간(50개 샘플데이터)으로 나눈다. [단계 2] 회귀분석 구간의 데이터를 이용하여 n-차 다항식모델의 파라미터를 추정한다. [단계 3] 추정된 회귀모델을 기반으로 미래의 값(20-step ahead)을 예측한다. [단계 4] 예측된 값과 실제 값의 오차를 구하여 저장한다. [단계 5] 한 스텝씩 이동시키면서 수집된 데이터의 전 구간에 대하여 [단계 1]~[단계 4]의 방법으로 RMS오차를 구한다.

Figure 3:

Fitting and prediction regions for polynomial regression for a given data set

본 논문에서는 미래의 값을 현재 시간으로부터 100ms후의 값(20-step ahead data)으로 간주하였고, 다항식모델의 차수를 3으로 결정하였다. 그 이유는 3차 다항식 모델로 근사한 경우에서 최소의 RMS오차를 보였으며, 이는 n-차 다항식 회귀분석에 있어 최적의 모델로 간주되기 때문이다.

3.2 실험결과

본 논문에서는 ARMA모델의 AR계수 및 MA계수에 대한 차수를 Box-Jenkins의 방법[11]을 토대로 자기상관함수(autocorrelation function) 및 부분자기상관함수(partial autocorrelation function)을 분석하여 각각 p = 10, q = 2로 설정하였다. Figure 2에서 도시된 x_α의 데이터 집합은 제안된 학습 알고리즘에 적용되어 ARMA모델 파라미터의 추정에 이용되었다.

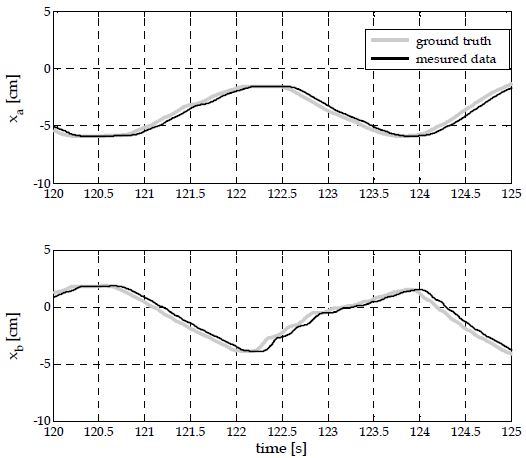
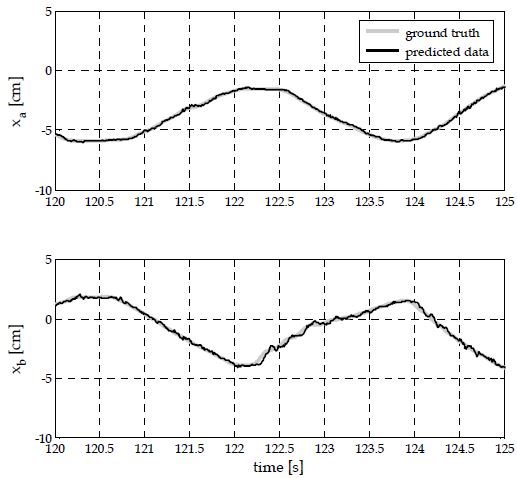
이렇게 학습된 모델은 두 햅틱데이터 집합 x_α, x_b에 각각 적용되었고, 예측 시스템을 통해 얻은 값들을 토대로 예측성능이 평가되었다. 보다 구체적으로, 본 논문에서는 시간 t에서 100ms (20 step-ahead)이후의 값을 예측할 경우에 대한 성능을 평가하였다. Figure 4는 Figure 2에 나타난 데이터를 100ms만큼 시간이동 시킨 후 원래의 데이터와 비교한 것이다. 여기서 시간 축은 120-125초의 범위를 가지도록 조정되었는데, 이는 오차의 정도를 직관적으로 확인하기 위함이다. Figure 5은 제안된 방법을 통해 예측된 결과를 나타낸다. Figure 4와 비교할 때, 제안된 방법을 통한 예측값들은 원래의 신호에 근접해 있음을 알 수 있다. Figure 5에서 x_α데이터의 예측결과에 비해 x_b 데이터의 예측결과가 평활도(smoothness) 관점에서 다소 낮아 보이는 이유는 학습과정에 있어 x_b의 데이터는 포함되지 않았기 때문이다. 그럼에도 불구하고, 이와 같은 결과가 얻어진 것은 x_b의 데이터에게도 학습된 ARMA 모델이 비교적 적합하다는 것이며 이에 따른 예측성능이 발휘되고 있음을 시사한다.

Figure 4:

Comparison between the ground truth and 100ms-shifted data

Figure 5:

Comparison between the ground truth and 100ms-ahead predicted data

Figure 6은 제안된 방법을 전체 데이터 집합에 적용한 경우의 RMS 예측오차들을 출력한 것이다. 일부 예측오차가 다소 큰 부근이 있으나 비교적 0.5cm이하에 분포하고 있음을 알 수 있다. Table 1은 전체 데이터 집합에 대한 평균 RMS 오차를 열거한 것이다. 예측성능의 비교를 위하여 3차 다항식 회귀분석 결과와 함께 나타내었다. 3차 다항식 회귀분석 결과는 RMS 평균 0.43cm정도의 예측성능을 보이고 있는 반면, 제안된 방법을 통한 ARMA 모델의 경우 RMS 평균 0.1cm이하의 예측성능을 보이고 있다. 이러한 결과는 제안된 방법이 100ms의 시간지연 범위 내에서 양호한 예측성능을 가지고 있음을 시사한다.

Figure 6:

RMS errors between the ground truth and 100ms-ahead predicted data

Table 1:

Comparison of the proposed method with cubic polynomial regression in prediction performance