자유수면과 프로펠러의 상호작용에 관한 수치적 연구

1. 서 론

최근 파랑 중 운항하는 선박은 선체의 운동뿐만 아니라 저항의 증가를 겪기 때문에 황천 중 선체 부가저항에 대한 많은 연구가 이루어져 왔다. 파랑 중 운항하는 선박의 선미에 부착된 프로펠러 또한 복잡하고 다양한 운동과 파랑 조건에 의해 침수 깊이 및 유입 유동의 조건이 수시로 변하게 된다. 침수 깊이 변화는 프로펠러와 자유수면의 상호작용을 일으키게 되어 외부 공기의 수중 유입 현상(air ventilation)뿐만 아니라 프로펠러 날개가 자유수면을 관통하는 현상(surface piercing)이 발생하기도 한다. 그리고 일반적으로 프로펠러가 자유수면 근처에서 작동 시 수면에 파도가 생성됨으로 인해 프로펠러의 추력과 토오크는 감소하게 되고 프로펠러의 추진효율은 낮아지게 되는 것으로 알려져 있다.

자유수면 근처에서 작동하는 스러스터나 프로펠러의 공기유입 현상에 대해서는 이미 많은 연구가 이루어졌다. Kozlowska et al. [1]은 자유수면 아래에서 작동하는 스러스터에 있어 공기유입 현상(air ventilation)의 발생 원리 및 종류에 대해 전진비가 0인 bollard 조건에서 자세히 연구하였다. 공기유입 현상은 프로펠러 전방의 낮은 압력에 의해 깔때기 모양의 보오텍스 기둥이 프로펠러의 흡입면에서 형성되면서 나타나게 되며, 자유수면에서 프로펠러 축까지의 깊이가 프로펠러 반지름의 약 1.4배(h/R=1.4)가 되면 공기유입 현상이 일어날 수 있다는 결과를 보인 바 있다. 반면에, Kozlowska et al. [2]은 모형실험 및 수치해석을 통해 전진비에 따라 이 보다 낮은 침수 깊이에서도 공기유입 현상이 나타나지 않을 수 있음을 검증하였다. Park et al. [3] 은 부분 침수된 프로펠러가 자유수면을 관통하면서 나타나는 추력 및 토오크의 변화에 대한 실험을 수행하여 경험식을 제안하였으며, RANS를 활용하여 부분 침수 프로펠러의 추력 변화에 대해 연구하였다. Califano and Steen [4][5]는 팁 보오텍스가 프로펠러의 공기유입 현상에 중요한 역할을 함을 주장하였으며, 프로펠러의 동적부하 해석을 통해 공기유입이 일어나는 영역에 대해서도 조사하였다. Savio et al. [6]은 선박의 후류에서 작동하는 모형과 실선 프로펠러의 공기유입 현상에 대해 연구하였다. 그리고 Li et al. [7]는 RANS를 이용하여 프로펠러의 기울기에 따른 자유수면의 영향 및 추력과 토오크에 대한 변화를 연구하였다.

대부분의 연구들은 전진비가 거의 0에 가까운 조건에서 공기유입 현상에 대한 연구에 집중되어 있는 반면, Paik et al. [8]은 전진비가 J=0.72인 조건에서 선박해양플랜트연구소에서 설계된 KP505 프로펠러를 대상으로 PIV(Particle Image Velocimetry)를 이용하여 계측함으로써 자유수면 아래에서 회전하는 프로펠러에 의한 자유수면의 변화에 대한 연구를 수행하였다. Park [9]와 Paik et al. [10]은 수치해석을 통해 동일 프로펠러를 대상으로 자유수면과 고정벽면 등이 프로펠러 주위 유동에 미치는 영향에 대해 조사한 바 있다. 그리고, Lee et al. [11]은 선박의 흘수 변화를 통해 프로펠러 침수깊이에 따른 영향을 실험으로 보여주었다.

본 연구에서는 Paik et al. [8]이 실험한 동일한 조건에서 자유수면의 파형을 비교하여 수치해석 기법을 검증하였다. 그리고 침수깊이 및 유입유속에 따른 자유수면의 파형과 프로펠러의 추력 및 토오크 변화를 관찰함으로써, 자유수면 근처에서 작동하는 프로펠러와 자유수면의 상호작용에 대해 살펴보았다.

2. 수치해석 기법

2.2 대상 프로펠러 및 격자계

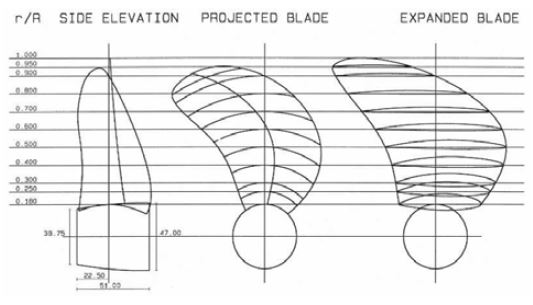
본 연구에 사용된 대상 프로펠러는 한국해양플랜트연구소에서 컨테이이너선을 대상으로 설계된 KP505 프로펠러이다. 본 연구에 사용된 KP505 모형 프로펠러의 주요 제원 및 형상은 Table 1 및 Figure 1과 같다. Paik et al.[8]의 모형시험에서 사용된 것과 동일한 크기의 모형을 본 연구에도 사용함으로서, 모형시험 결과와 비교를 통해 수치해석의 정확도를 검증하였다.

Table 1:

Principal particulars of KP505 model propeller

Figure 1:

Propeller drawing of KP505 model propeller

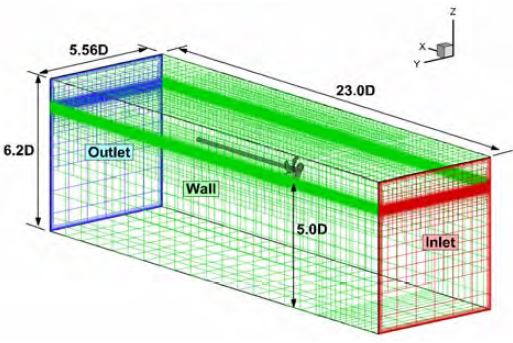
수치해석을 위한 계산영역은 Paik et al. [8]에서 사용한 회류수조와 동일한 조건을 적용하였다. 회류수조 관측부의 크기는 1.2m×0.3m×0.25m로 수심은 프로펠러 직경의 약 5배에 해당한다. 본 연구에 적용된 수치해석의 영역은 벽면 및 수심 등의 효과를 동일하게 모사하기 위해 회류수조 관측부 크기에 해당하는 영역을 Figure 2와 같이 설정하였으며, 계산영역의 측면에는 벽면조건을 적용하였다.

Figure 2:

Computational domain and boundary conditions

프로펠러 주위 격자는 trimmer 격자 생성법에 의한 비정렬 격자로 구성하였고, 프로펠러 날개 표면의 경계층은 프리즘 격자를 사용하여 y⁺<1이 되도록 구성하였다. 자유수면이 있는 경우에는 sliding mesh 기법을 적용하여 프로펠러의 비정상 회전운동을 모사하였다. 그리고 자유수면이 있는 곳과 프로펠러 팁 및 허브 보오텍스가 발생하는 곳에 Figure 3에 보인 바와 같이 격자를 집중시켰다. 본 연구에 사용된 격자수는 회전하는 프로펠러 영역에 약 1.6M 그리고 프로펠러 후류와 자유수면을 포함한 나머지 영역에 약 5.3M으로, 총 약 6.9M의 격자수가 사용되었다. 반면, 자유수면이 없는 경우에는 프로펠러 영역과 나머지 영역에 각각 약 2.0M과 3.2M의 격자가 사용되었다. 침수깊이비(h/R)는 Figure 3에 도시된 바와 같이, 자유수면에서 프로펠러 축 중심까지의 거리(h)를 프로펠러 반지름(R)에 대한 비로 나타낸 것이다.

Figure 3:

Grid system for propeller wake and free surface

3. 수치해석 결과

3.1 침수깊이비에 대한 영향

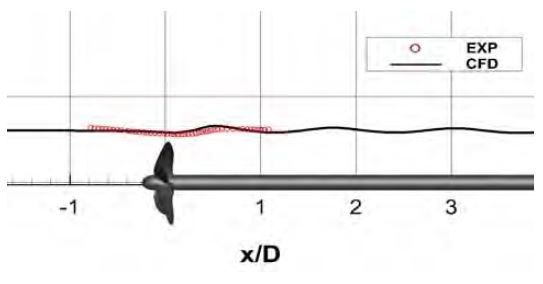
먼저 수치해석의 유효성을 검증하기 위해 Paik et al. [8]의 모형시험 결과와 수치해석 결과의 자유수면 파형을 Figure 4에 비교하였다. 시험과 해석 모두 전진비(J=V/nD)는 J=0.72에 해당하며, 프로펠러의 회전수는 8.37rps이고 유입유속은 0.325m/s이다. 이 때 침수깊이비는 h/R=1.2로 전진비가 낮은 상태에서는 프로펠러의 부하가 증가하기 때문에 공기유입현상이 일어날 수도 있다. 비정상 상태에서의 수치해석은 2.0°의 프로펠러 회전각에 대응하는 시간 간격으로 계산되었다.

Figure 4:

Comparison of wave profile at y/D = 0 with experimental data

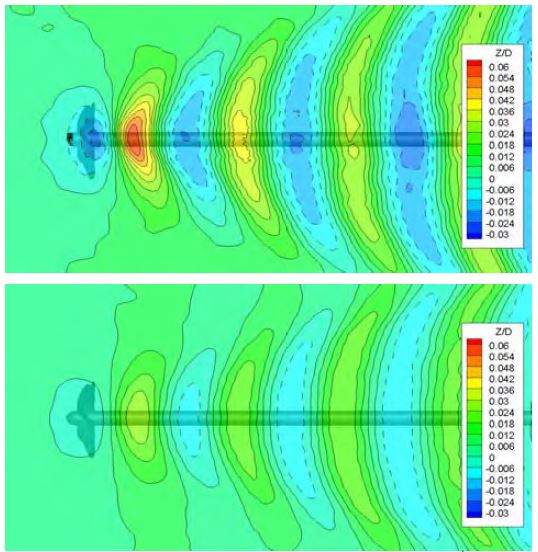
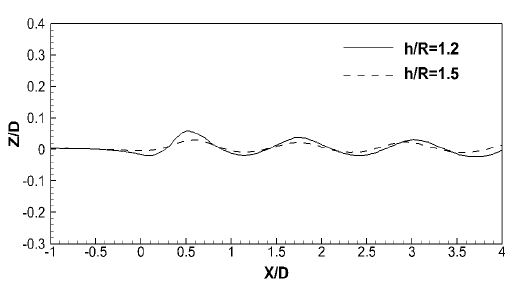
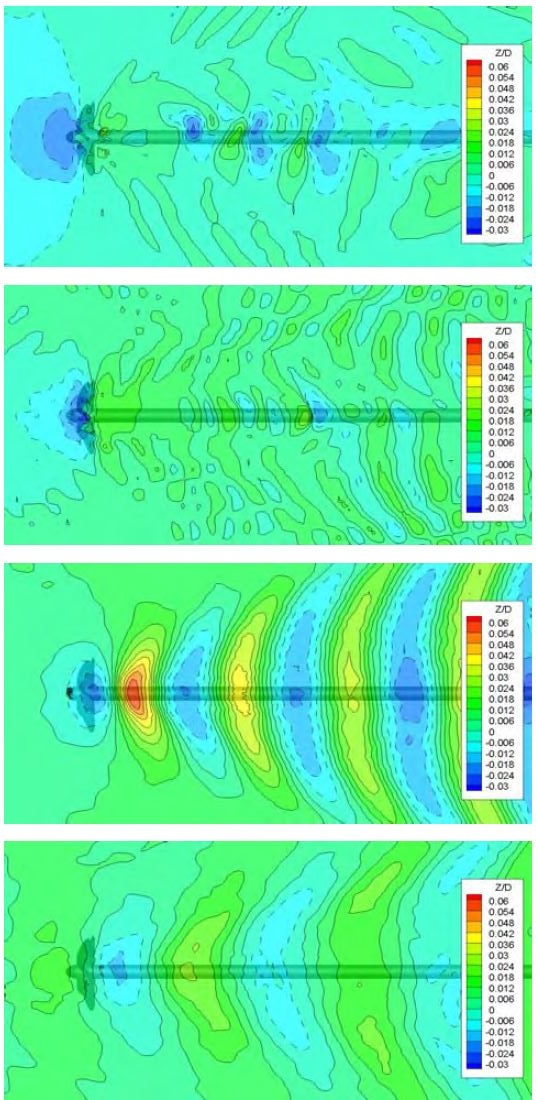
침수깊이비에 대한 영향을 파악하기 위해 h/R=1.5에서 해석된 자유수면 파형을 Figure 5에 비교하였다. 자유수면의 파형은 전형적인 Kelvin파의 모양을 띄고 있으며, 두 조건의 유입속도가 동일하기 때문에 침수깊이비에 따른 자유수면의 파장은 거의 유사하게 나타나지만 파고에는 다소 차이를 보이고 있다.

Figure 5:

Instantaneous free surface contours at h/R = 1.2 (top) and h/R = 1.5 (bottom)

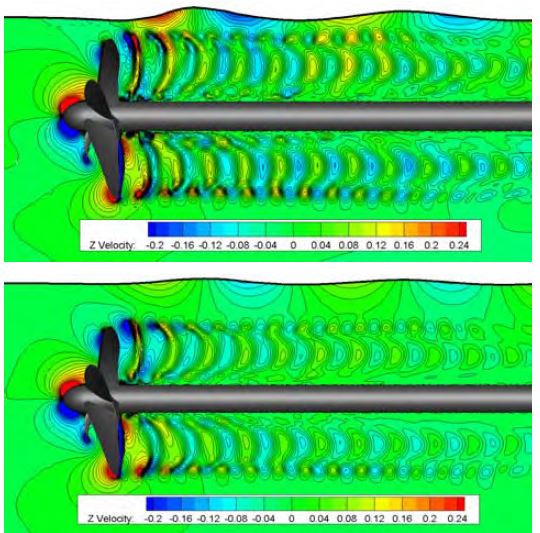
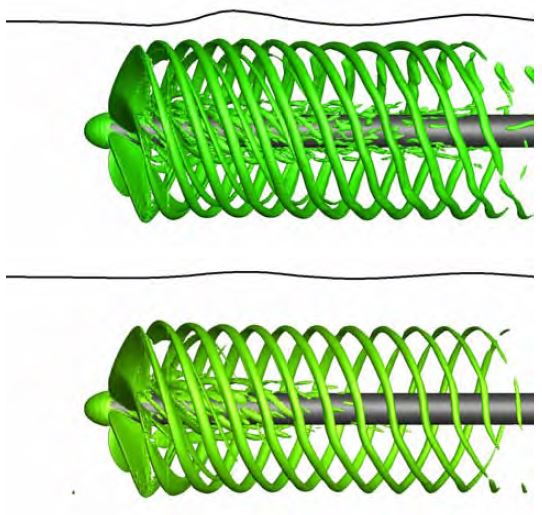
프로펠러 주위 유동의 수직방향 속도성분을 Figure 6에 비교하였다. 여기서, 수직방향 속도는 유입유속으로 무차원화된 값이다. 자유수면 파형이 형성되는 영역의 수면 하부의 수직방향 성분이 침수깊이비에 따라 확연한 차이로 보이고 있을 뿐만 아니라, 프로펠러 후류의 수직방향 성분도 차이를 보이고 있다. Figure 7에 나타난 Q-criterion iso-surface에서도 프로펠러와 자유수면의 상호작용에 의한 이러한 차이를 확인할 수 있다.

Figure 6:

Instantaneous vertical velocity contours at h/R = 1.2 (top) and h/R = 1.5 (bottom)

Figure 7:

Instantaneous iso-surfaces of Q-criterion (Q = 500) at h/R = 1.2 (top) and h/R = 1.5 (bottom)

프로펠러 축이 위치한 y/D=0.0에서의 파형을 Figure 8에 침수깊이비에 따라 비교하였다. 앞서 설명한 바와 같이 두 침수깊이비에 따라 파장은 거의 차이가 없으나, 파고는 다소 큰 차이를 보이고 있다. 특히, 프로펠러 날개 상부에서 발생하는 최초 파저의 크기에서 큰 차이를 보이고 있다.

Figure 8:

Comparison of wave profile according to submerged depth at y/D = 0

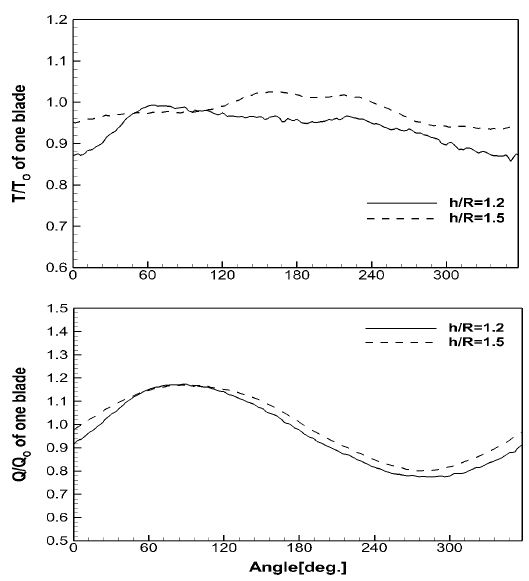
두 조건 모두에서 자유수면의 파형은 생성되었으나, 공기유입 현상은 발생하지 않았다. 따라서 프로펠러 추력 및 토오크의 변화는 오로지 자유수면 파형과의 상호작용에 의해서만 발생한다. Figure 9는 프로펠러 날개 한 개가 일회전하는 동안의 추력 및 토오크의 변화를 자유수면이 없는 경우(h/R=∞)의 추력 및 토오크에 대한 비로 나타낸 것이다. 날개 각도 별 추력 변화가 두 조건에서 약간 상이한 결과를 보인다. 이는 Figure 8에 보인 바와 같이 h/R=1.2에서는 프로펠러 상부에서 파저가 뚜렷하게 나타난 반면, h/R=1.5에서는 프로펠러 상부에서 파저가 나타나지 않고 하류에서 파정이 바로 나타나는 자유수면 파형의 특성 차이로 인한 것으로 판단된다. 하지만 토오크의 변화는 두 경우 모두에서 거의 유사한 경향을 보이고 있다. Table 2에 요약된 바와 같이, 평균 추력 및 토오크가 h/R=1.2에서는 각각 6.1%, 3.7% 감소하였으며, 상대적으로 자유수면의 영향을 적게 받는 h/R=1.5에서는 각각 2.1%, 0.1% 감소하였다.

Table 2:

Thrust and torque ratios according to submerged depth

Figure 9:

Angular variations of thrust (top) and torque (bottom) ratios according to submerged depth

3.2 전진비에 대한 영향

침수깊이비가 h/R=1.2인 상태에서 전진비에 따른 자유수면 파형, 프로펠러 주위 유동 및 프로펠러 성능 변화를 조사하기 위해, 전전비 J=0.3,0.5,0.72,0.9에서 수치해석을 수행하였다. 전진비는 프로펠러 회전수를 8.37rps로 고정하고 유입유속을 변경을 통해 변화시켰다.

전진비의 변화에 따른 자유수면 파형의 모양을 Figure 10에 비교하였다. 전진비 J=0.3 및 J=0.5에서는 유입유동의 속도가 낮기 때문에 J=0.72에서와 같이 일정한 파형이 생성되지 않는다. 그리고 전진비 J=0.9에서는 파형이 생성되지만, 유입유동이 속도가 빠르기 때문에 상대적으로 파장이 길고 파고는 낮다. 한 가지 특이한 현상은 프로펠러 주위에 발생하는 최초 파저의 위치가 전진비에 따라 변한다는 것이다. 전진비 J=0.3에서는 프로펠러 흡입면의 전방에서 파저가 발생하고, 전진비가 증가하면서 파저의 위치는 조금씩 뒤로 이동하게 된다. 그리고 전진비 J=0.9가 되면 파저는 압력면의 하류에서 발생함을 알 수 있다.

Figure 10:

Instantaneous free surface contours at J = 0.3,0.5,0.72,0.9 (from top to bottom)

이러한 현상은 Figure 11에 도시된 수직방향 속도분포에서 더욱 자세히 설명될 수 있다. 전진비가 낮은 J=0.3에서의 속도분포를 보면, 자유수면 근처에 위치한 프로펠러 날개 흡입면의 전방에는 아래 방향으로 향하는 속도성분이 그리고 가장 아래에 위치한 날개 흡입면에는 위로 향하는 속도성분이 강하게 나타난다. 이는 프로펠러 날개 압력면에서 흡입면으로 감아 돌아가는 팁 보오텍스에 의해 발생하는 것이다. 이러한 팁 보오텍스는 날개의 후류에 발생하는 음과 양의 수직방향 속도성분의 쌍으로 나타난다. 전진비가 증가하면서 날개 흡입면에 발생하는 수직방향 속도의 크기는 점점 감소하게 되고, 프로펠러 부하가 적은 전진비 J=0.9에서는 날개 흡입면의 속도보다 후연 보오텍스에서의 속도 성분이 더욱 크게 나타난다. 즉, 프로펠러 날개의 부하에 따라 날개 흡입면에서 발생하는 수직방향 속도성분의 크기가 바뀌게 되고, 이로 인해 자유수면의 파저가 발생하는 위치도 변경됨을 알 수 있다.

Figure 11:

Instantaneous vertical velocity contours at J = 0.3,0.5,0.72,0.9 (from top to bottom)

Kozlowska et al. [2]에서 전진비에 따라 침수깊이비가 h/R=1.4보다 낮은 침수 깊이에서도 공기유입 현상이 나타나지 않을 수 있음을 지적한 바와 같이, 본 연구에서 전진비 J=0.3에서도 공기유입 현상은 나타나지 않았다.

전진비에 따른 프로펠러 날개 표면의 압력분포는 Figure 12과 같다. 앞에서 설명한 바와 같이, 전진비가 낮은 영역에서는 날개 흡입면과 압력면의 압력차이 커서 팁 보오텍스가 강하게 발생하게 되며, 전진비가 높은 영역에서는 압력차이가 상대적으로 적어 팁 보오텍스가 약하게 발생하게 됨을 확인할 수 있다. 그리고 자유수면과의 상호작용에 의해 상부에 위치한 날개의 압력 크기가 하부에 위치한 날개의 압력 크기보다 작음을 관찰할 수 있다. 이것으로부터 프로펠러 날개에 작용하는 추력과 토오크가 날개의 위치에 따라 변화됨을 예측할 수 있다.

Figure 12:

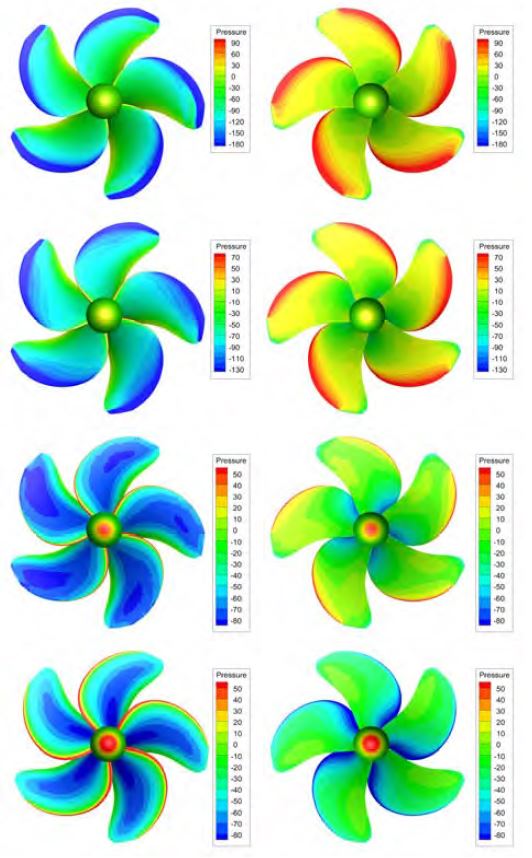
Instantaneous pressure distributions on suction (left) and pressure (right) sides of propeller blade at J = 0.3,0.5,0.72,0.9 (from top to bottom)

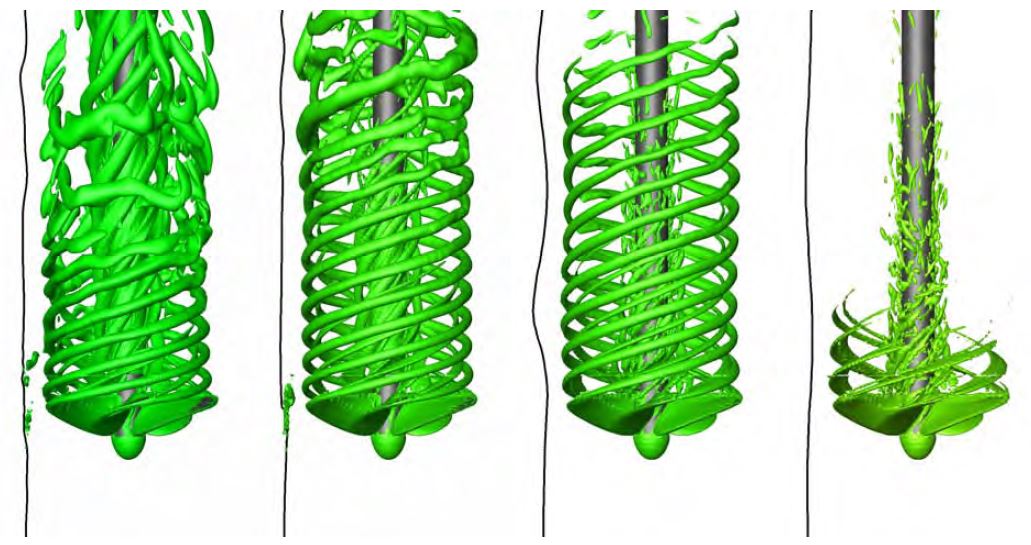
전진비 변화에 따른 Q-criterion iso-surface를 Figure 13에 비교하였다. Figure 11과 Figure 12에서 관찰한 바와 같이 낮은 전진비에서는 강한 팁 보오텍스가 발생하고, 높은 전진비에서는 팁 보오텍스가 아주 약함을 관찰할 수 있다. 전진비 J=0.5와 J=0.72에서는 팁 보오텍스가 길게 빠져나가는 반면, J=0.3과 J=0.9에서는 팁 보오텍스의 길이가 상대적으로 짧게 나타났다. J=0.3은 전진비가 작아 프로펠러 후류가 길게 빠져나지 못하기 때문이고, J=0.9에서는 팁 보오텍스의 강도가 너무 약해 후류에서 쉽게 소산되기 때문으로 판단된다.

Figure 13:

Instantaneous iso-surfaces of Q-criterion (Q = 500) at J = 0.3,0.5,0.72,0.9 (from top to bottom)

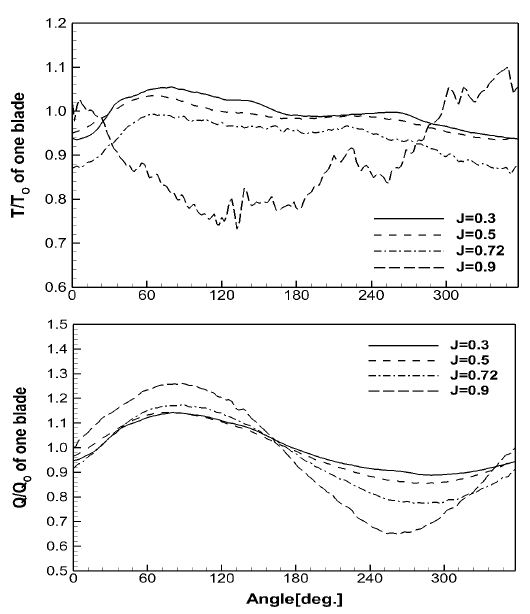
프로펠러 날개 한 개가 일회전 하는 동안의 추력 및 토오크의 변화를 자유수면이 없는 경우(h/R=∞)와 비교하여 Figure 14에 도시하였다. 전진비 J=0.9를 제외하고 모든 경우에서 프로펠러 날개 위치에 따른 추력 변화가 동일한 경향을 보이고 있다. Figure 10의 자유수면 파형에서 살펴본 바와 같이 전진비 J=0.9에서는 최초 파저 위치가 프로펠러 날개 후류에 위치하기 때문에 프로펠러 날개와 자유수면이 느끼는 상호작용에 위상차가 나타나는 것으로 판단된다. 반면에 토오크는 모든 전진비에서 유사한 형태로 변화되고 있다.

Figure 14:

Angular variations of thrust (top) and torque (bottom) ratios of h/R = 1.2 to h/R = ∞

자유수면이 없는 조건(h/R=∞)에 대비한 h/R=1.2에서의 추력과 토오크의 비를 Table 3에 요약하였다. 낮은 전진비(J=0.3,0.5)에서의 추력과 토오크의 감소량은 2% 이내이며, 추진효율의 변화는 거의 없다. 하지만, J=0.72에서는 추력과 토오크가 각각 6.1%, 3.3% 감소하여 추진효율은 2.4% 감소하게 된다. J=0.9에서의 추력 및 토오크 감소량은 더욱 증가하여 각각 11.0%, 3.4%이고, 추진효율은 7.8% 감소한다. 즉, 공기유입 현상이 발생하지 않는 조선에서는 전진비가 높아질수록 자유수면과의 상호작용에 의해 프로펠러의 추력 및 토오크의 감소량은 증가하고, 추력의 감소량이 토오크이 감소량보다 커서 추진효율의 감소량도 증가함을 알 수 있다.

Table 3:

Thrust and torque ratios of h/R = 1.2 to h/R = ∞

4. 결 론

본 논문에서는 자유수면 근처에서 작동하는 프로펠러의 성능대해 수치해석을 통해 연구하였다. 수치해석은 RANS를 적용하였으며, 자유수면의 효과를 확인하기 위해 VOF 기법을 사용하였다. 수치해석 기법은 KP505 프로펠러로 회류수조에서 계측된 자유수면 파형과 비교함으로써 검증하였다.

침수깊이비에 따른 자유수면 파형 및 프로펠러 추력 및 토오크의 변화를 확인하기 위해 h/R=1.2와 h/R=1.5에서 수치해석을 수행하였다. 두 경우 모두 Kelvin파를 형성하며, 유사한 파장을 가지고 있지만 파고에서는 상당한 차이를 보였다. 그리고 침수깊이비가 작을수록 자유수면과의 상호작용이 증가하여 추력 및 토오크의 감소량이 증가함을 확인하였다.

전진비에 따른 영향을 검토하기 위해 침수깊이비 h/R=1.2에서 전전비를 J=0.3,0.5,0.72,0.9로 바꾸어 가며 수치해석을 수행하였다. 전진비가 가장 낮은 J=0.3에서도 공기유입 현상은 관찰되지 않았지만, 전진비에 따른 프로펠러 주위 유동 특성에 따라 자유수면의 파형이 바뀌게 됨을 확인하였다. 특히, 전진비가 증가함에 따라 팁 보오텍스의 크기는 약해지고, 이로 인해 자유수면의 최초 파저 위치가 프로펠러 후류 방향으로 이동하게 됨을 관찰하였다. 그리고 공기유입 현상이 발생하지 않는 조건에서는 전진비가 증가할수록 추력 및 토오크의 감소량이 증가하게 됨을 확인하였다. 추력의 감소량이 토오크이 감소량보다 급격하게 증가하여 프로펠러의 효율도 감소하게 됨을 확인하였다.

향후 수치해석 결과를 모형시험을 통해 검증하는 연구를 수행할 예정이며, 특히 동일 전진비에서 유입유속 및 프로펠러 회전수를 변경에 따른 영향을 연구함으로써 낮은 전진비에서 공기유입 현상이 발생할 수 있는 물리적 조건에 대한 연구가 추가적으로 수행되어야 할 것으로 판단된다.

Acknowledgments

본 논문은 산업통상자원부 해양플랜트특성화대학의 지원을 받아 수행되었습니다.

References

• A. M. Kozlowska, S. Steen, and K. Koushan, “Classification of different type of propeller ventilation and ventilation inception mechanism”, First International Symposium on Marine Propulors, smp’09, June, Trondheim, Norway, (2009).
• A. M. Kozlowska, K. Wöckner, S. Steen, T. Rung, K. Kousan, and S. J. B. Spence, “Numerical and experimental study of propeller ventialtion”, Second International Symposium on Marine Propulors, smp’11, June, Hamburg, Germany, (2011).
• H. G. Park, T. G. Lee, K. J. Paik, and S. H. Choi, “Study on the characteristics of thrust and torque for partially submerged propeller”, Journal of the Korean Society for Marine Environmental Engineering, vol. 14(no. 4), p264-272, (2011). [https://doi.org/10.7846/JKOSMEE.2011.14.4.264]
• A. Califano, and S. Steen, “Numerical simulations of a fully submerged propeller subject to ventilation”, Ocean Engineering, vol. 38(no. 14-15), p1582-1599, (2011). [https://doi.org/10.1016/j.oceaneng.2011.07.010]
• A. Califano, and S. Steen, “Identification of ventilation regimes of a marine propeller by means of dynamic- loads analysis”, Ocean Engineering, vol. 38(no. 14-15), p1600-1610, (2011). [https://doi.org/10.1016/j.oceaneng.2011.07.009]
• L. Savio, S. Spence, K. Koushan, and S. Steen, “Full scale and model scale porpeller ventilation behind ship”, Third International Symposium on Marine Propulors, smp’13, May, Tasmania, Australia, (2013).
• Y. Li, E. Martin, T. Michael, and M. Carrica, “A study of propeller operation near a free surface”, Journal of Ship Research, vol. 59(no. 4), p190-200, (2015). [https://doi.org/10.5957/JOSR.59.4.150042]
• B. G. Paik, J. Y. Lee, and S. J. Lee, “Effect of propeller immersion depth on the flow around a marine propeller”, Journal of Ship Research, vol. 52(no. 2), p102-113, (2008).
• I. R. Park, “Numerical analysis of flow around propeller rotating beneath free surface”, Journal of Ocean Engineering and Technology, vol. 29(no. 6), p427-435, (2015). [https://doi.org/10.5574/KSOE.2015.29.6.427]
• B. G. Paik, C. M. Lee, and S. J. Lee, “Comparative measurements on the flow structure of a marine propeller wake between an open free surface and closed surface flows”, Journal of Marine Science and Technology, vol. 10(no. 3), p123-130, (2005). [https://doi.org/10.1007/s00773-004-0190-x]
• J. Y. Lee, B. G. Paik, and S. J. Lee, “PIV measurements of hull wake behind a container ship model with varying loading condition”, Ocean Engineering, vol. 36(no. 5), p377-385, (2009). [https://doi.org/10.1016/j.oceaneng.2009.01.006]
• F. R. Menter, “Two-equation eddy-viscosity turbulence models for engineering applications”, AIAA Journal, vol. 32(no. 8), p1598-1605, (1994). [https://doi.org/10.2514/3.12149]