A study on hydrodynamic coefficients estimation of modelling ship using system identification method

1. Introduction

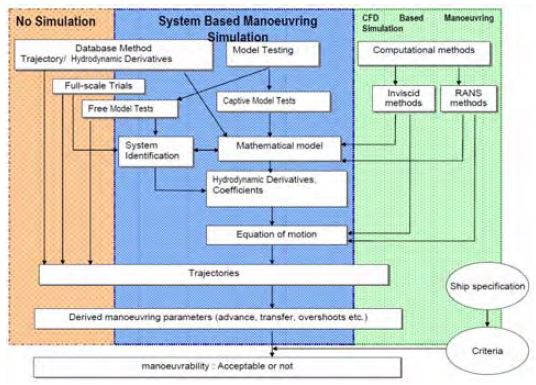
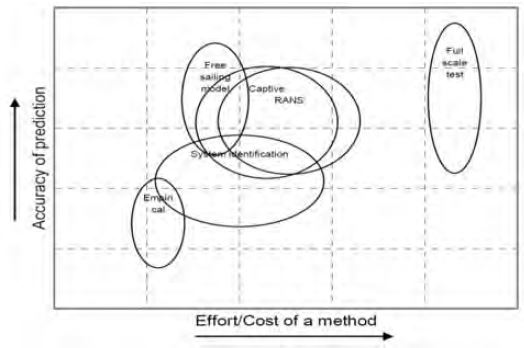
Mathematical modelling is one of the important part to predict ship’s manoeuvrability. Especially for the submerged part of the hull, the forces and moments acting on the hull can be presented by hydrodynamic coefficients. As shown in Figure 1, International Towing Tank Conference (ITTC) summarized different methods to estimate hydrodynamic coefficients for the ship’s manoeuvrability[1]. Figure 2 shows that each method has its own accuracy to effort/cost characteristics and Captive model test and Computational Fluid Dynamics (CFD) method are common at design stage[2][3]. These methods are the most reliable source of hydrodynamic coefficients excluding full scale trials, but the relatively high cost and calculation time are required than empirical method and system identification.

Figure 1:

Overview of manoeuvring prediction methods

Figure 2:

Effort/cost versus accuracy of manoeuvring prediction methods

This paper examines a new estimation method which is based on the system identification method with full scale sea trial data. This method estimates the hydrodynamic coefficients in a ship’s mathematical model by using mathematical optimization algorithm. The algorithm conducts manoeuvring simulation and compares with benchmark data, such as sea trial data, at every iteration and it provides updated target variables to be optimized.

Various ideas on the system identification has been studied with the progress of computational calculation. Abkowitz [4] conducted full scale sea trial and firstly applied Extended Kalman Filter (EKF) and Rhee et al. [5] and Zhang et al. [6] applied System Based (SB) free running tests with the EKF algorithm. Tran et al. [7] introduced SQP and BFGS algorithms to get optimal results.

As a preliminary study, a set of simulation result, which used manually tuned double ended ferry ship model corresponding to sea trial data, is selected as a benchmark data to be optimized. The Interior-point algorithm optimizes four linear hull coefficients and presents optimization results and corresponding simulation results.

This paper presents a system identification method based on a new optimization algorithm and its optimization results. Comparison among the benchmark data, the initial condition of the optimization process and finally tuned data are also presented in this paper.

2. Ship modelling and benchmark data

2.1 Mathematical model

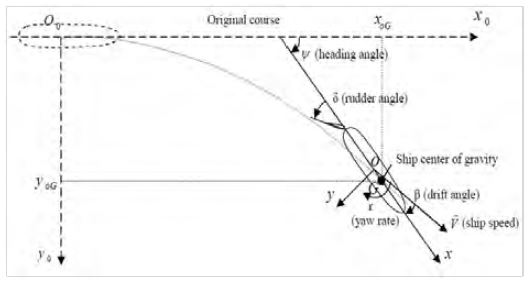
3-Degrees-of-Freedom (DOF) of the ship-fixed and earth-fixed coordinate systems are adopted in this study as shown in Figure 3 [8]. The O₀-x₀y₀ plane and the O-xy plane lie on the undisturbed free surface, with the x₀ axis pointing in the direction of the original heading of the ship, whereas the z₀ axis and the z axis point downwards vertically. The angle between the directions of the x₀ axis and the x axis is defined as the heading angle, ψ.

Figure 3:

Coordinate system of the vessel

In the simulation of optimization process, mathematical model of Rheinmetall Defence simulator is used to predict ship’s manoeuvrability. When a ship is considered as a massive and rigid body, forces and moment acting on the hull and on the ship-fixed coordinate system on the ship’s center of gravity can be described as Equation (1), according to the Newtonian law of motion.

$\[ \begin{array}{c}X=m\left(\stackrel{\text{̇}}{u}-\mathit{vr}\right)\\ Y=m\left(\stackrel{\text{̇}}{v}-\mathit{ur}\right)\\ N=I_z\bullet \stackrel{\text{̇}}{r}\end{array} \]$

(1)

Forces and moment of the model are consisted with multiple modules as Equation (2): hull, propeller, rudder and other external forces and moments. The external factors are not considered in this study.

$\[ \begin{array}{c}X=X_H+X_P+X_R\\ Y=Y_H+Y_P+Y_R\\ N=N_H+N_P+N_R\end{array} \]$

(2)

Equation (3) shows the composition of the hydrodynamic forces and moment acting on the hull. In this model, the empirical regression formulas of Norrbin[9] and Clarke [10] are applied to calculate the initial hydrodynamic coefficients. Each hydrodynamic coefficients can be expressed the function of ship’s main dimension as Equation (4): length, beam, draught and displacement of the ship. Y_non and N_non are non-linear components of sway force and yaw moment. These non-linear components are dependent on the position of the ship’s turning point.

$\[ \begin{array}{c}{X}_H^{\text{'}}=X_{up}\stackrel{\text{̇}}{u}+X_{vr}^{\text{'}}vr+X_{uu}^{\text{'}}u\left|u\right|+X_{u4}^{\text{'}}{u}^3\left|u\right|+X_{uvvv}^{\text{'}}{uv}^2\left|v\right|\\ Y_H^{\text{'}}=Y_{vp}^{\text{'}}\dot{v}+Y_{rp}^{\text{'}}\dot{r}+Y_{ur}^{\text{'}}ur+Y_{uv}^{\text{'}}\left|u\right|v+Y_{non}^{\text{'}}\\ N_H^{\text{'}}=N_{rp}^{\text{'}}\dot{r}+N_{vp}^{\text{'}}\dot{v}+N_{ur}^{\text{'}}\left|u\right|r+N_{uv}^{\text{'}}uv+N_{non}^{\text{'}}\end{array} \]$

(3)

$\[ \left\{Y_{\mathit{uv}}^{\text{'}},Y_{\mathit{ur}}^{\text{'}},N_{\mathit{uv}}^{\text{'}},N_{\mathit{ur}}^{\text{'}}\right\}=f\left(L,B,T,△\right) \]$

(4)

2.2 Benchmark data

Motor ferry ‘Prins Richard’ is adopted as a benchmark vessel to conduct optimization trials and Figure 4 shows the vessel. This RoPax (Roll-on Roll-off Passenger) and on-board railway vessel offers liner service between Puttgarden, Germany and Rødby, Denmark. It applies the ‘double-ended ferry’ structure, which has a specific hull form and a propulsion system, allowing ahead and astern manoeuvring without turning the vessel. These hull forms can save manoeuvring time or berthing in the harbour. Due to its specific character, the identical shapes of the bow and stern, the term “astern manoeuvre” does not exist for this type of vessel. They are typically on short crossing routes, which have confined ferry terminals and shallow channel conditions [11].

Figure 4:

M/F Prins Richard

As shown in Table 1, the technical table of the vessel, this ferry equips two pairs of podded contra-rotating propulsion units, which are combined systems for the steering and propulsion modules.

Table 1:

Main particular of M/F Prins Richard

The benchmark data of the optimization process is provided by the simulation software, programmed by MATLAB/ Simulink. Technical data and model data of the benchmark ship is brought from Maritime Simulation Center Warnemünde (MSCW) and ISSIMS Institute of Hochschule Wismar in Germany.

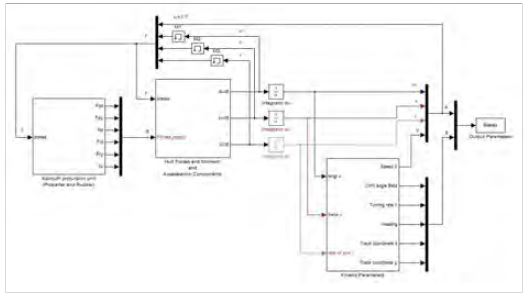
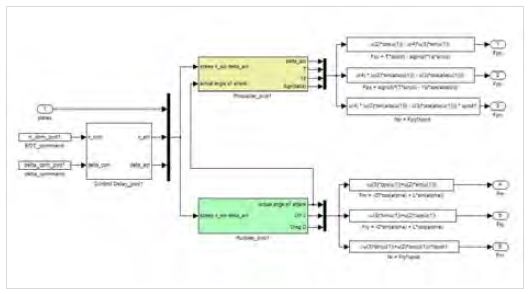
The simulation software consists three modules as shown in Figure 5: Pod, Hull and Kinetic parameter. Figure 6 shows the module of pod unit. Maximum four podded units are allowed to use and each unit has two subunits, propulsion and rudder. Contrary to conventional propeller and rudder ships, the command angle of the podded propulsion unit controller manoeuvres in the opposite direction due to its thrust. Thus, a rudder command angle should be given in the opposite direction to the direction to be manoeuvred. When the rudder and RPM commands are given to the model, the propeller/rudder forces and moments are calculated through this part. The kinetic parameter module returns ship's speed, drift angle, turning rate, heading and track coordinates through the velocity components on each axis.

Figure 5:

Overview of simulation software

Figure 6:

Podded propulsion module

Table 2 shows a comparison of four linear hydrodynamic coefficients of sway force and yaw moment. The value 'Benchmark' is the coefficients which are manually tuned for the MSCW simulator and 'Norrbin' is the calculated coefficients according to the empirical regression formulas of the MSCW simulator.

Table 2:

Benchmark data and regression values of hydrodynamic coefficients

3. Optimization of hydrodynamic coefficients

3.1 Mathematical optimization

Mathematical or numerical optimization is the minimization or maximization of a function subject to constraints on its variables[ 12]. This can be written as Equation (5):

$\[ \underset{x\in R^n}{\mathrm{minf}\left(x\right),}\mathrm{subject\; to} \]$

(5)

c_i(x) ＝ 0, i ∈ E

c_i(x) ≥ 0, i ∈ I

where,

- x is the variable, which has to be optimized and normally it should be a form of vector;
- f is the objective function, a function which returns scalar and it contains the information of minimization or maximization;
- c_i are constraints, which sets equations and inequality condition those the variable x must satisfy during whole optimization process.

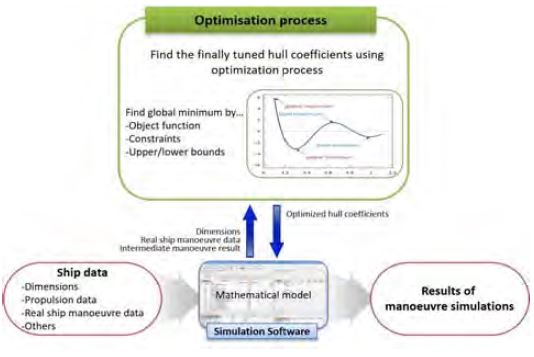
Optimization Toolbox of MATLAB calculates various kinds of optimization problems, such as constrained problems, unconstrained continuous and discrete problems, through widely used optimization solvers and algorithms. Figure 7 shows the whole process of the mathematical optimization to get tuned hydrodynamic coefficients.

Figure 7:

Concept flow of the mathematical optimization

The solvers need a certain objective function, which provides a minimum or a maximum value relating to the optimization of target values. In order to improve the reliability and accuracy of the result of the optimization process, additional constraints in the toolbox may be required. Lower and upper bound, linear and nonlinear equalities and linear and nonlinear inequalities are representational constraints of the optimization process.

3.2 Optimization conditions

Table 3 shows an overall condition of the optimization process. The interior point method is one of the algorithms to solve linear and nonlinear convex optimization problems. It provides an optimal solution by traversing the interior of the feasible region. In this study, four linear hydrodynamic coefficients of sway force and yaw moment are selected as input variables and seven different objective function and constraints are provided to the optimization process. Turning manoeuvre with 10 degrees and 35 degrees of rudder angle and zigzag manoeuvre with 10 degrees of rudder angle are used for the optimization. Advance and tactical diameter of the turning manoeuvre, first and second overshoot angle of the zigzag manoeuvre are the detailed items to be compared with the objective and constraint functions.

Table 3:

Detailed conditions of optimization

where,

- Obj: Objective function
- Con: Nonlinear equality constraints
- Adv :Advance from turning manoeuvre
- Tac: Tactical diameter from turning manoeuvre
- Ovst: Overshoot angle from zigzag manoeuvre

The initial variable and lower and upper bounds are also important conditions of the optimization. They limit the range of the variables of the optimization. The initial variable is the value of 'Norrbin' in Table 2. The optimization will start from the original regression value. The values of lower and upper bounds are calculated –50% and 200% of ship's original dimensions, which affects the calculation of hydrodynamic coefficients, respectively.

4. Verification of optimization results

Table 4 shows the optimization results and compares their manoeuvre characteristics with the benchmark data and initial regression data. Manoeuvring data from the turning circle test with rudder angle 10 and 35 degrees and the zigzag test with rudder angle 10 degrees were used for comparison. As shown in the table, result of Case 1 is almost the same with the benchmark data. Results of Case 5 and Case 7 are also close to the benchmark data than others. It is supposed that at least two different manoeuvres with various rudder angle are required to get successful optimization results. However Case 6 showed that the overshoot angles of the zigzag manoeuvre are not proper for the condition of the objective function. Results of Case 1, 5 and 7 are similar with the benchmark data. Other results show restricted manoeuvring characteristics corresponding to their conditions of the objective function and constraints, respectively.

Table 4:

Optimization results

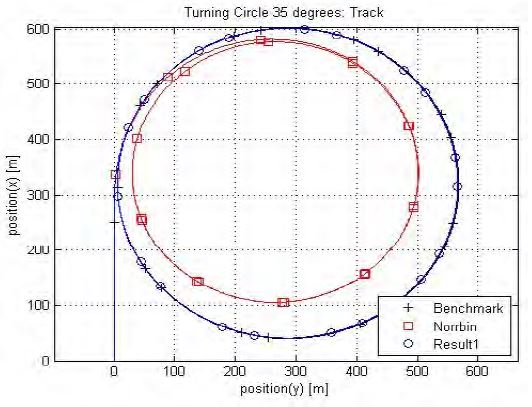
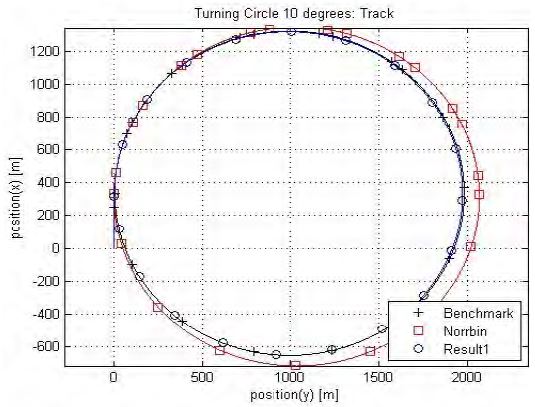
Figures 8-10 compare simulation results of the benchmark data, results using the Norrbin coefficients and the results of the optimization results of case 1. The optimized simulation is fitted to the trajectory of the benchmark data.

Figure 8:

Result of optimization: Turning circle 35

Figure 9:

Result of optimization: Turning circle 10

Figure 10:

Result of optimization: Zigzag 10/10

Table 5 and Figure 11 show how long the algorithm needs to find the optimal results. During 35 steps of the overall optimization process, actual optimization is completed near the 10th step. After that, minor corrections to find the minimum between the benchmark data and the optimized data are continuing until the end of the process.

Table 5:

Optimization histories of coefficients

Figure 11:

Optimizing histories of coefficients

5. Conclusion

This paper studied an optimization process to suggest a tuning process for ship modelling. The turning manoeuvre with rudder angel 35 degrees and 10 degrees and zigzag manoeuvre with rudder angle 10 degrees were carried out to compare between the benchmark data and the optimized data. A short brief of this study is as follows:

Firstly a double-ended ferry with two pairs of azimuth propulsion units was adopted as the target vessel. Prior to the optimization process, modelling the vessel was carried out by MATLAB/Simulink. The mathematical model was borrowed from the model of MSCW simulator in Germany.

Secondly, an optimization algorithm and multiple optimal conditions of the objective function and nonlinear equality constraints, were provided to be verified. Turning manoeuvre and zigzag manoeuvre and their manoeuvre characteristics were used to the optimization conditions and verification.

Finally, optimized results for easy case are compared with the benchmark simulation data. The optimal conditions which apply at least two different manoeuvres with various rudder angle showed satisfactory simulation results compared to the benchmark data. There was a limit for other optimization conditions where the simulation result could not satisfy for all manoeuvres.

However, the target values of this study were limited to four linear hydrodynamic derivatives and even though these four values have dominant influence on the manoeuvring characteristics of certain vessels, there is a need for additional research to optimize more hydrodynamic derivatives for certain mathematical models. Also the environmental influence should be considered in the future studies.

References

• International Towing Tank Conference, “The manoeuvring committee: Final report and recommendations to the 25th ITTC”, Proceedings of 25th ITTC, vol. 1, p145-152, (2008).
• P. Oltmann, “Identification of hydrodynamic damping derivatives - A progmatic approach”, International Conference on Marine Simulation and Ship Manoeuvrability, vol. 3(Paper 3), p1-9, (2003).
• J. Seils, Die Identifikation der hydrodynamischen Parameter eines mathematischen Modells fur die gesteuerte Schiffsbewegung mit Verfahren der nichtlinearen Optimierung, Ph.D Dissertation, Fakultät für Mathematik, Natur- und Technikwissenschaften, Hochschule für Seefahrt Warnemünde-Wustrow, Germany, (1990), (in German).
• M. A. Abkowitz, “Measurement of hydrodynamic characteristics from ship maneuvering trials by system identification”, Society of Naval Architects and Marine Engineers, vol. 88, p283-318, (1980).
• K. Rhee, and K. Kim, “A new sea trial method for estimating hydrodynamic derivatives”, Journal of Ship and Ocean Technology, vol. 3(no. 3), p25-44, (1999).
• X. Zhang, and Z. Zou, “Identification of Abkowitz model for ship manoeuvring motion using ϵ-support vector regression”, Journal of hydrodynamics, vol. 23(No. 3), p353-360, (2011). [https://doi.org/10.1016/S1001-6058(10)60123-0]
• K. T. Tran, A. Ouahsine, F. Hissel, and P. Sergent, “Identification of hydrodynamic coefficients from sea trials for ship maneuvering simulation”, Proceedings of Transport Research Arena 5th conference, (2014).
• Z. Zou, Ship manoeuvring and seakeeping, Shanghai, China, Shanghai Jiao Tong University, (2006).
• N. H. Norrbin, Theory and Observations on the Use of a Mathematical Model for Ship Manoeuvring in Deep and Confined Waters, Technical report of Swedish Steel Producers Association (SSPA), No. 68, Gothenburg, Sweden, (1971).
• D. Clarke, P. Gedling, and G. Hine, “The application of manoeuvring criteria in hull design using linear theory”, Royal Institution of Naval Architects, Vol. 125, p45-68, (1983).
• A. Minchev, C. Simonsen, and R. Zilcken, “Double-ended ferries: propulsive performance challenges and model testing verification”, Proceedings of the second International Symposium on Marine Propulsor, Hamburg, (2011).
• J. Nocedal, and S. J. Wright, Numerical optimization, Second edition, Springer, (2006).