밀리미터파 기반 상향링크 하이브리드 빔포밍 시스템을 위한 빔선택 방법

1. 서 론

초고속 데이터 전송 무선 시스템에 대한 수요 증가에 따라[1], 밀리미터파 (millimeter-wave) 주파수 대역의 풍부한 가용 주파수자원을 이용한 밀리미터파 통신 기술이 주목을 받고 있다[2]. 밀리미터파 통신 기술은 데이터 전송 용량을 획기적으로 개선할 수 있는 기술이긴 하나, 높은 주파수 대역으로 인한 전송 손실이 크다는 단점이 있다[3]. 이러한 전송 손실은 밀리미터파의 짧은 파장을 이용해 대용량 안테나를 집적함으로써 보상할 수 있다. 이에 맞춰 최근에 아날로그와 디지털 신호 처리를 결합한 하이브리드 빔포밍 (hybrid beamforming) 다중 안테나 기술에 대한 연구가 활발하다 [4]-[6]. 하이브리드 빔포밍 기술로는 아날로그 하드웨어의 제약; 아날로그 위상 조절기의 이득 제약, 위상 제어기 낮은 해상도 등을 극복하기 위해, 채널의 공분산을 이용하는 방법[6], 주요 고유벡터 (dominant eigenvector) 를 이용하는 방법[4][7] 등이 알려져 있다. 이러한 하이브리드 빔포밍 방법은 대부분 하향링크 시스템을 전제로 연구되었다.

본 논문에서는 아날로그 하드웨어의 회로적 제약을 감안해 상용 통신 방식인 3GPP (3rd generation partnership project) LTE (Long-term evolution) 규격에서 도입한 이산 푸리에 변환 행렬 기반 고정형 빔을 적용한 상향링크 하이브리드 빔포밍 시스템의 구조를 소개하고[8], 상향링크 사용자간 간섭을 제거하는 제로-포싱 (zero-forcing) 기지국 수신기 구조를 제안한다. 사용자 단말기의 전력 제약 및 하드웨어 복잡도를 고려해 각 단말기가 여러 개의 빔 중 하나를 선택해 신호를 전송하는 빔포밍 시스템에서 전송용량을 개선할 수 있는 빔 선택 방법을 제안한다. 또한 제안하는 빔 선택 방법의 전송 용량 개선 효과를 컴퓨터 시뮬레이션을 통해 확인한다.

본 논문에서의 표기법은 다음과 같다. 굵은 대문자와 소문자는 각각 행렬과 벡터를 표시한다. 임의의 행렬 X에 대해, X^T, X^*, X^H는 각각 X의 transpose, conjugate, 그리고 Hermitian transpose를 의미한다. 또한 임의의 벡터 x에 대해 diag(x)는 x를 대각 성분으로 갖는 대각행렬을 나타낸다. In은 크기 n×n인 identity 행렬을 의미한다.

2. 시스템 모델

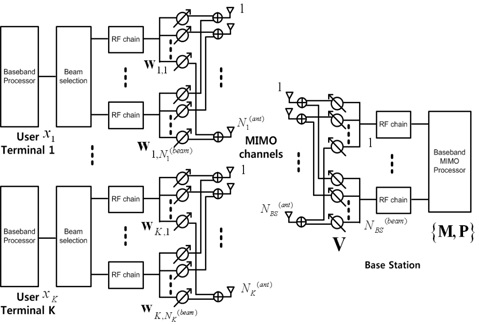
본 논문에서는 Figure 1과 같은 밀리미터파 기반 다중 송수신 안테나 상향링크 시스템을 고려한다. 다수의 사용자가 해당 단말기의 빔 (beam) 을 이용해 신호를 전송하고, 기지국은 다수의 빔으로 신호를 수신한다. 기지국은 $$ N_{\mathit{BS}}^{\left(\mathit{ant}\right)}$$ 개 안테나를 이용해 생성한 $$ N_{\mathit{BS}}^{\left(\mathit{beam}\right)}$$ 개 빔으로 K명 사용자 단말기가 동시에 전송하는 상향링크 신호를 수신한다. 이 때 임의의 k (1≤k≤K) 번째 사용자 단말기는 $$ N_k^{\left(\mathit{ant}\right)}$$ 개의 안테나와 무선주파수대역에서 생성한 빔으로 신호를 전송한다. 본 논문에서는 무선주파수대역 하드웨어 복잡도 및 전력 소비를 고려해 기지국 및 단말기의 아날로그 빔 개수는 해당 안테나 개수보다 작다고 가정한다, 즉, $$ N_{\mathit{BS}}^{\left(\mathit{beam}\right)}\le N_{\mathit{BS}}^{\left(\mathit{ant}\right)},N_k^{\left(\mathit{beam}\right)}\le N_k^{\left(\mathit{ant}\right)}$$, ∀k[4][7].

Figure 1:

Milimeter wave based uplink hybrid beamforming systems

임의의 k 번째 단말기의 기저대역 (baseband) 신호 x_k에 대해 빔선택기 출력 신호는 다음과 같다.

여기서 $$ e_k^{\left(j\right)}$$는 크기 $$ N_k^{\left(\mathit{beam}\right)}$$×1의 벡터로 j 번째 성분만 ‘1’ 이고 나머지는 모두 ‘0’ 이다.

상기 빔 선택기를 통해 x_k는 j 번째 빔포밍 계수 $$ w_k^{\left(j\right)}$$ 로 빔포밍되어 전송된다. 아날로그 및 디지털 빔포밍을 함께 수행하는 하이브리드 빔포밍 시스템에서 아날로그 빔포밍 계수는 채널의 공분산 행렬을 이용하는 방법과 고유벡터를 이용하는 방법[4][7] 등이 있다. 본 논문에서는 상용 셀룰러 통신 규격인 3GPP LTE에서 사용하는 이산푸리에변환 행렬 기반 빔 계수를 적용한다[8][10][11]. 즉 각각의 빔 계수는 이산푸리에변환 행렬의 열(column) 벡터로 한다. 여기서 N-point 이산푸리에변환 행렬 D_N의 i 행, j 열 성분은 다음과 같이 나타낼 수 있다.

본 논문에서는 무선주파수대역 하드웨어의 복잡도를 고려해, 호 설정 (call-setup) 이후 통신이 종료될 때까지 아날로그 빔 계수 {$$ w_k^{\left(j\right)}$$}가 일정한 ‘고정형’ 아날로그 빔포밍으로 가정한다. 기지국은 다음 식과 같이 상향링크 무선 채널을 통해 각 단말기의 송신 신호를 수신한다.

여기서 $$ {\mathrm{W}}_{\mathrm{k}}=\left\{{\mathrm{w}}_{\mathrm{k}}^{\left(1\right)},\cdots ,{\mathrm{w}}_{\mathrm{k}}^{\left({\mathrm{N}}_{\mathrm{k}}^{\left(\mathrm{beam}\right)}\right)}\right\},{\gamma }_k=\sqrt{P_k/{\sigma }_x^2}$$는 k번째 사용자 단말기의 송신 전력 계수, P_k는 최대 송신 전력, $$ \mathrm{E}\left\{{\left|x_k\right|}^2\right\}={\sigma }_x^2$$, n은 백색 가우시안 잡음 (additive white Gaussian noise) 으로 각 성분의 평균은 ‘0’, 분산은 $$ {\sigma }_k^2$$, 그리고 H_k는 기지국과 k번째 단말기간의 무선 채널을 나타내며 quasi-static 모델로 가정한다. 전파의 산란이 많이 발생하는 특성을 갖는 2 GHz 대역의 셀룰러 채널과 달리 밀리미터파 대역 채널은 제한된 산란 특성을 갖는다[1][2]. 밀리미터파 대역 채널은 기하학적 채널 모델을 이용해 다음과 같이 모델링할 수 있다. L개 산란 매체가 있을 때, 각 산란 매체는 기지국과 단말기 사이에 하나의 전송 경로를 형성함을 가정하면 k번째 사용자 단말기와 기지국간 채널은 다음과 같이 나타낼 수 있다.

여기서 ρ_k와 $$ {\alpha }_l^{\left(k\right)}$$는 각각 기지국과 k번째 단말기간의 경로 손실과 l번째 경로의 복소 이득을 나타낸다 (1≤l≤L). 경로 별 진폭은 레일레이 분포를 따른다 가정한다. 즉 $$ {\alpha }_l^{\left(k\right)}$$ 는 평균 ‘0’ 분산 $$ \overline{P_R}$$의 정규 분포를 따른다. $$ \overline{P_R}$$는 평균 전력 이득을 의미한다. 변수 $$ {\theta }_l^{\left(k\right)}\in \left[\mathrm{0,2}\pi \right]$$와 $$ {\varphi }_l^{\left(k\right)}\in \left[\mathrm{0,2}\pi \right]$$는 각각 기지국에서 k번째 단말기 사이의 l번째 경로에 대한 도달각 (Angle of arrival) 와 시작각 (Angle of departure)를 의미한다¹⁾. 그리고 $$ a_{\mathit{MS}}\left({\theta }_l^{\left(k\right)}\right)$$ 와 $$ a_{\mathit{BS}}\left({\varphi }_l^{\left(k\right)}\right)$$는 각각 단말기와 기지국의 안테나 배열 응답 벡터 (antenna array response vector) 이다. 본 논문에서 제안하는 알고리즘과 결과는 임의의 안테나 배열 구조에 대해 적용가능하다. 편의상 본 논문의 시뮬레이션 결과는 등간격 선형 배열 (uniform linear arrray) 안테나를 사용한다. 상기 안테나를 가정할 경우, 기지국 안테나 배열 응답 벡터 $$ a_{\mathit{BS}}\left({\varphi }_l^{\left(k\right)}\right)$$는 다음과 같이 나타낼 수 있다.

여기서 λ는 신호의 파장, d는 각 성분 안테나간 거리, 그리고 $$ {\Delta }_l^{\left(k\right)}=j\frac{2\mathit{\pi d}\mathit{sin}\left({\varphi }_l^{\left(k\right)}\right)}{\lambda }$$ 의미한다. 단말기의 안테나 배열 응답 벡터, $$ \left\{a_{\mathit{MS}}\left({\theta }_l^{\left(k\right)}\right)\right\}$$도 같은 방법으로 표현할 수 있다. 상기 채널 모델은 다음과 같이 행렬을 이용해 간결히 표현할 수 있다.

여기서 $$ a^{\left(k\right)}=\sqrt{\frac{N_{\mathit{BS}}^{\left(\mathit{ant}\right)}{N}_k^{\left(\mathit{ant}\right)}}{{\rho }^{\left(k\right)}}}{\left[{\alpha }_1^{\left(k\right)},\cdots ,{\alpha }_L^{\left(k\right)}\right]}^T$$ 로 정의한다. 그리고 $$ A_{\mathit{BS}}^{\left(k\right)}=\left[a_{\mathit{BS}}\left({\varphi }_1^{\left(k\right)}\right),a_{\mathit{BS}}\left({\varphi }_2^{\left(k\right)}\right),\cdots ,a_{\mathit{BS}}\left({\varphi }_L^{\left(k\right)}\right)\right]$$ 와 $$ A_{MS}^{\left(k\right)}=\left[a_{MS}\left({\theta }_1^{\left(k\right)}\right),a_{MS}\left({\theta }_2^{\left(k\right)}\right),\cdots ,a_{MS}\left({\theta }_L^{\left(k\right)}\right)\right]$$는 각각 기지국과 k번째 단말기의 L개 전송 경로에 대한 안테나 배열 응답 벡터를 포함한 행렬이다.

식 (6)을 이용해 수신 신호 (3-2)는 다음과 같이 행렬 형태로 표현할 수 있다.

여기서 $$ \mathrm{H}=\left[{\mathrm{H}}_1,\cdots ,{\mathrm{H}}_{\mathrm{K}}\right],\mathrm{W}=\left[{\mathrm{w}}_1^{\left(\mathrm{j}\right)},\cdots ,{\mathrm{w}}_{\mathrm{K}}^{\left(\mathrm{j}\right)}\right],\mathrm{\Gamma }=\mathrm{diag}\left\{{\mathrm{\gamma }}_1,\cdots ,{\mathrm{\gamma }}_{\mathrm{K}}\right\}$$, 그리고 $$ \mathrm{x}={\left[x_1,\cdots ,x_K\right]}^T$$ 이다 (각 단말기가 선택한 빔포밍 계수는 j번째 빔으로 가정하고, W에서 j에 대한 표시는 생략한다).

3. 밀리미터파 기반 상향링크 하이브리드 빔포밍 시스템 설계

본 절에서는 제로-포싱 기반 기지국 기저대역 수신기를 설계하고 더불어 시스템 전송 용량을 증대하는 단말기 빔 선택 알고리즘을 제시한다.

3.2 전송 용량 증대를 위한 단말 빔 선택 방법

앞에서 구한 전송 용량 (13)은 모든 사용자 단말기가 해당 단말의 아날로그 빔 중 j 번째 빔을 선택하는 것으로 가정하고 유도하였다. 그러나 각 사용자 별로 임의의 빔을 선택할 수 있도록 행렬 W²⁾을 일반화 하면 다음과 같다.

$\[ W\left(\left\{e_k^{\left(j\right)}\right\}\right)=\left[\left[w_1^{\left(1\right)},\cdots ,w_1^{\left(N_1^{\left(beam\right)}\right)}\right]\ddots \left[w_1^{\left(1\right)},\cdots ,w_1^{\left(N_k^{\left(beam\right)}\right)}\right]\right]\times \left[e_1,\cdots ,e_K\right] \]$

(14)

여기서 k 번째 단말기의 빔 선택 벡터 $$ e_k\in R^{N_k^{\left(\mathit{beam}\right)\times 1}}$$은 하나의 성분만 ‘1’이고 나머지 모든 성분은 ‘0’이다. 단말기의 빔선택 방법에 따라 전송 용량은 달라지므로, 여기서는 다음과 같은 최적화 문제를 만들 수 있다.

$\[ \begin{array}{c}\left\{e_k^{*}\right\}={\mathrm{argmaxR}}_{\mathrm{\Sigma }}\\ \mathit{s.t.}\left\{e_k^{\left(j\right)}\right\}\end{array} \]$

(15)

최적화 문제 (15)는 비선형 그리고 non-convex 문제이므로, 분석적 해 (analytical solution)을 구하기가 어렵다. 대신에 포괄적 검색 (exhaustive search)방법, 즉 각 단말기 별로 가능한 모든 빔포밍 벡터를 대입해 해를 찾는 방법으로 최적 해를 구할 수 있다. 하지만 이 방법은 사용자 단말기 개수 K와 선택 가능한 빔 개수 $$ N_{MS}^{\left(\mathit{beam}\right)}$$가 증가할수록 탐색 공간 (search space)의 크기 $$ K_{\mathit{BS}}^{N^{\left(\mathit{beam}\right)}}$$가 커지므로, 사용자 단말기 개수가 많거나 선택 가능한 빔 개수가 많은 경우 사용하기 어렵다.

수신 신호 (9)에서, 수신기 기저대역 유효 채널 (effective channel) 을 다음과 같이 정의할 수 있다.

$\[ H_{\mathit{eff}}={\mathit{MV}}^H\mathit{HW}\left(\left\{e_k\right\}\right)\Gamma \]$

(16)

제로-포싱 수신기 적용시, 유효 채널 H_eff의 각 열 벡터가 서로 직교하면 유효 채널에 대한 의사 역변환 연산은 단순한 회전 연산이 되어 수신 채널 이득의 손실은 거의 없게 된다[12]. 이를 이용해 사용자간 유효 채널 벡터가 서로 직교에 가깝게 되도록 빔을 선택하는 Algorithm 1을 제안한다.

Algorithm 1의 동작 원리는 다음과 같다. Step 2에서 Φ_i의 각 사용자별 유효채널을 {g₍₁₎,⋯,g_(i-1)}에 대한 직교 여공간 (orthogonal complement) 으로 투영 (projection) 한다. 이전 반복 연산에서 {g₍₁₎,⋯,g_(i-1)}에 부분직교(semi-orthogonal)하지 않는 사용자별 유효채널벡터는 Φ_i에서 제거했으므로, Φ_i의 각 사용자별 유효채널벡터는 {g₍₁₎,⋯,g_(i-1)}에 부분직교하다. Step 3에서 유효채널 벡터 중 투사된 값(norm)이 가장 큰 벡터를 선택하고, 이것이 다음 기준 (basis) 벡터 g_(i)가 된다. 이러한 과정에 대한 반복 연산이 종료되면, Ψ₀에는 각 사용자별로 선택된 빔포밍 벡터 색인자 (index) 가 저장된다.

Algorithm 1과 같은 부분 직교 기반 빔포밍 벡터 선택 방법, 또는 스케쥴링 (scheduling) 방법은 다중 사용자 하향링크 시스템에서 이미 알려져 있다[12]. 제안하는 Algorithm 1과 참고 문헌[12]의 알고리즘은 Step 1 ~ Step 3까지 유사하다. 그러나 기존 방법은 하향링크 빔포밍 사용자를 찾는 알고리즘으로 각 사용자별 오직 한 개 벡터를 찾는다. 반면 제안하는 알고리즘은 상향링크에서 사용자별 한 개 이상의 빔과 그것들로 구성된 유효 채널 벡터 집합을 구하는 것이다. 그래서 기존 방법과 달리 제안하는 알고리즘은 단계 4 에서 각 사용자별로 선택된 유효 채널 벡터 개수의 합을 각 사용자별로 지원 가능한 빔 개수와 비교해 처리하는 과정이 필요하다. 만약 사용자별로 선택된 빔 개수가 지원 가능한 빔 개수를 초과하면 해당 사용자의 나머지 빔들은 다음 반복 연산 과정의 Φ_i+1에서 제외된다.

4. 시뮬레이션 결과

제안하는 빔선택 방법의 성능을 확인하기 위해 다음과 같은 밀리미터파 상향링크 채널에 대해 시뮬레이션을 수행한다. 2 절에서 설명한 채널 모델에서 $$ {\overline{P}}_R=1$$, 산란 경로 개수 L=3 으로 한다. 시작각과 도달각은 [0,2π]에서 일정하게 분포 (uniformly distributed) 한다 가정한다. 그리고 밀리미터파 전송 시스템의 반송파는 28 GHz, 대역폭은 100 MHz, 그리고 경로 손실 계수 (pass loss exponent)는 3 으로 가정한다. 기지국 안테나 개수 $$ N_{BS}^{\left(\mathit{ant}\right)}=32$$, 기지국 빔 개수 또는 기지국 무선주파수 대역 빔 수신기 개수 $$ N_{BS}^{\left(\mathit{beam}\right)}=4$$, 사용자 단말기 개수 K=4, 사용자 단말기의 안테나 개수 $$ N_k^{\left(\mathit{ant}\right)}=8$$, ∀k 그리고 단말기의 송신 전력 P_k=1, ∀k, 단말기에서 선택할 수 있는 최대 빔의 개수 $$ N_k^{\left(\mathit{beam}\right)}=1$$, ∀k 로 가정한다. 안테나는 간격이 λ/2인 등간격 선형 배열 (uniform linear arrary) 안테나를 적용한다 (여기서 λ는 28 GHz 에 해당하는 파장을 의미한다).

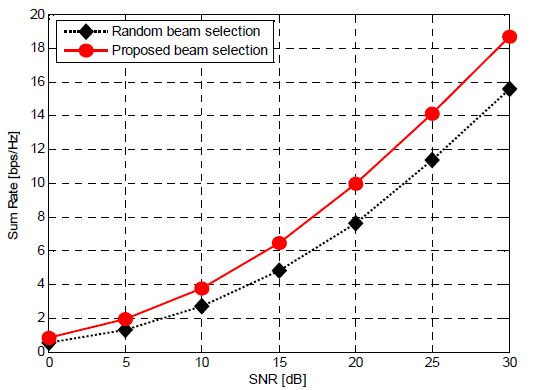
Figure 2는 상기한 실험 환경에서 구한 전송 용량이다. 사용자 단말기가 임의의 빔을 선택해 적용하는 무작위 (random) 빔선택 방법과 성능을 비교한다. 제안하는 빔선택 방법은 각 사용자간 빔을 서로 직교에 가깝게 선택함으로써, 30 [dB]의 신호 대 잡음비 (signal-to-noise ratio; SNR) 에서 무작위 빔선택 방법 대비 약 30 % 의 전송 성능 향상 효과를 확인할 수 있다.

Figure 2:

The sum-rate performances

5. 결 론

본 논문에서는 밀리미터파 기반 상향링크 하이브리드 빔포밍 시스템의 송수신기 구조 및 전송 용량 개선을 위한 빔선택 방법을 제안하였다. 각 송수신기는 무선주파수 대역의 하드웨어의 제약을 고려해, 이산푸리에변환 행렬 기반 고정형 아날로그 빔포밍 방법을 적용하였다. 상향링크 다중 사용자간 간섭을 제거하기 위해 기저대역 기지국 다중 안테나 프로세서로 제로-포싱 (zero-forcing) 수신 방법을 적용하였고, 상향 링크 유효 채널, 즉 무선채널과 빔포밍 행렬의 곱이 서로 직교 (orthogonal)에 가깝도록 선택함으로써 전송 용량을 개선하는 방법을 제안하였다. 또한 시뮬레이션을 통해 제안하는 빔선택 방법의 성능 개선 효과를 확인하였다.

References

• Y. Guo, D. Liu, and N. Bird, “Guest editorial for the special issue on antennas and propagation aspects of 60–z90 GHz wireless communications”, IEEE Transactions on Antennas and Propagation, vol. 57(no. 10), p2817-g2819, (2009). [https://doi.org/10.1109/TAP.2009.2032587]
• R. Daniels, and R. Heath, “60 GHz wireless communications: Emerging requirements and design recommendations”, IEEE Vehicular Technology Magazine, vol. 2(no. 3), p41-z50, (2007). [https://doi.org/10.1109/MVT.2008.915320]
• S. Rangan, T. S. Rappaport, and E. Erkip, “Millimeter-wave cellular wireless networks: Potential and challenges”, Proceedings of IEEE, vol. 102(no. 3), p366-385, (2014). [https://doi.org/10.1109/JPROC.2014.2299397]
• A. Alkhateeb, O. Ayach, G. Leus, and R. W. Heath, “Channel estimation and hybrid precoding for millimeter wave cellular systems”, IEEE Journal on Selected Areas in Communications, vol. 8(no. 5), p831-846, (2014). [https://doi.org/10.1109/jstsp.2014.2334278]
• J. Nsenga, A. Bourdoux, and F. Horlin, “Mixed analog/digital beamforming for 60 GHz MIMO frequency selective channels”, Proceedings of the IEEE International Conference on Communications, p1-z6, (2010). [https://doi.org/10.1109/icc.2010.5502689]
• A. Adhikary, J. Nam, J. Ahn, and G. Caire, “Joint spatial division and multiplexing –The large-scale array regime”, IEEE Transactions on Information Theory, vol. 59(no. 10), (2013). [https://doi.org/10.1109/TIT.2013.2269476]
• E. Ayach, S. Rajagopal, S. Abu-Surra, Z. Pi, and R. W. Heath, “Spatially sparse pecoding in millimeter wave MIMO systems”, IEEE Trans. on Wireless Communications, vol. 13(no. 3), p1499-1513, (2014). [https://doi.org/10.1109/TWC.2014.011714.130846]
• Results on zero-forcing MU-MIMO, Freescale Semiconductor, 3rd Generation Partnership Project Technical Specification Group Radio Access Network Working Group 1 Technical Report, R1-071511, (2007).
• G. H. Golub, and C. F. V. Loan, Matrix Computation, Baltimore, U.S.A., Johns Hopkins, (1996).
• Evolved Universal Terrestrial Radio Access (E-UTRA), 3rd Generation Partnership Project Technical Specification 36.211, Version12.4.5 (Release 12), (2015).
• D. Yang, L. Yang, and L. Hanzo, “DFT-based beamforming weight-vector codebook design for spatially correlated channels in the unitary precoding aided multiuser downlink”, Proceedings of the IEEE International Conference on Communications, p1-5, (2010). [https://doi.org/10.1109/icc.2010.5502350]
• T. Yoo, and A. Goldsmith, “On the optimality of multiantenna broadcast scheduling using zero-forcing beamforming”, IEEE Journal on Selected Areas in Communications, vol. 24(no. 3), p528-541, (2006). [https://doi.org/10.1109/JSAC.2005.862421]