전산유체역학을 이용한 해양작업지원선의 빌지킬 유무에 따른 횡동요 성능에 관한 연구
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 상용 점성 유동 해석 소프트웨어인 Star-CCM+를 이용하여 110m급 해양작업지원선의 빌지킬 효과에 따른 횡동요 성능에 관한 연구를 수행하였다. 해양작업지원선에 관한 연구에 앞서 DTMB 5512 선형에 대한 수치 시뮬레이션을 통해 실험과 비교 검증하였다. 검증된 결과를 바탕으로 빌지킬 유무에 따른 해양작업지원선의 자유 횡동요 시뮬레이션을 수행하였으며, 이를 통해 각각의 무차원 감쇠 계수와 횡동요 응답진폭함수를 산출하였다.
Abstract
In this study, numerical simulations on the effects of bilge keel on roll motion were conducted. The numerical simulations were performed on a 110 m class PSV using the commercial viscous flow analysis software Star-CCM+. Before conducting the study on the 110 m class PSV, an additional simulation of DTMB 5512 was performed and compared with the experimental results to validate the feasibility of the numerical simulation. In the simulation on PSV, a nondimensional damping coefficient was calculated using a free roll decay simulation, and the response amplitude operator (RAO) for the roll motion was calculated with a nondimensional damping coefficient at two conditions (with/without bilge keel).
Keywords:
Platform supply vessel, Bilge keel, Free roll motion, Numerical simulation, Non-dimensional damping coefficient키워드:
해양작업지원선, 빌지킬, 자유 횡동요, 수치 시뮬레이션, 무차원 감쇠 계수1. 서 론
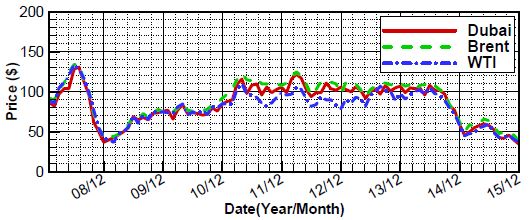
최근 세계적인 경기 침체와 셰일가스와 같은 대체 에너지 개발로 인해 Figure 1과 같이 유가는 지속적으로 하락하고 있으며, 저유가의 영향으로 해양자원 개발과 관련된 프로젝트 등이 중단되는 등 해양 자원 개발에 어려움을 겪고 있다[1]. 하지만 육상에 한정된 에너지 자원은 점차 고갈될 것이며, 이에 따라 미래의 안정적인 에너지 자원 확보를 위해서라도 해양 자원 개발은 필수적이다. 또한 해양자원 개발을 위한 구조물들은 선박이 건조되어 온 기간에 비해 상대적으로 짧기 때문에 경제성 확보를 위해서도 지속적인 연구개발이 필요하다.
해양자원을 개발하기 위한 선박 및 구조물은 한 곳에 오랜 기간 동안 계류되거나 고정되어 작업을 수행함에 따라 이동이 어렵다[2]. 따라서 작업 기간 동안 유지보수 및 물자를 공급받기 위해서는 별도의 운반용 선박이 필요하며, 이런 작업을 수행하는 선박을 해양작업지원선이라 한다.
이런 해양작업지원선은 해상에서 작업을 수행함에 따라 파도, 조류, 바람 등과 같은 해상상태에서 안정적으로 작업성을 유지하기 위해 선박의 내항성능이 중요하며, Seo et al. [3]는 해양플랜트지원선의 내항성능과 관련된 연구로 26m급 해양플랜트지원선에 대하여 저항성능 및 운동성능을 파악하기 위해 상용소프트웨어를 사용하여 다양한 해상조건에서 저항성능 및 운동성능을 추정하였다.
선박의 내항 성능은 주로 실험적 방법 및 시뮬레이션을 이용한 방법 등을 통해 평가되고 있다. 실험적 방법은 다른 방법들에 비해 상대적으로 많은 시간과 금액이 소요되나 정확도가 높으며 시뮬레이션 방법은 포텐셜 이론을 이용한 방법이 널리 이동되고 있다. 하지만 상대적으로 점성의 영향이 크게 작용하며 비선형성이 강하게 나타나는 횡동요의 경우 포텐셜 이론을 이용한 선박의 운동 성능 추정에 한계가 있으며, 이를 보완하기 위해 자유 횡동요 감쇠실험을 통해 산출되는 감쇠계수를 이용하는 방법이 사용하고 있다. 이와 관련된 연구로 Kim et al. [4]은 선박의 자유 횡동요 실험을 통해 다양한 횡동요 감쇠계수 산출방법에 따른 감쇠계수를 비교 분석하여 장단점을 파악하였으며, Irvine et al. [5]은 DTMB 5512 모델을 이용한 수조 실험 자료를 기반으로 선박의 횡동요에 대한 연구를 수행하였다. 그리고 Jung et al. [6]은 사각형 바지선의 횡동요 성능 파악을 위한 실험적 연구로 입사파에 따른 횡동요 성능에 관한 연구를 수행하였다.
또한 상대적으로 비용과 시간이 많이 소요되는 실험을 대체하기 위한 수단으로 점성 효과를 고려할 수 있는 전산유체역학을 적용한 연구로, Bae et al. [7]은 상용 소프트웨어인 Fluent의 이동격자법(Sliding mesh)을 이용하여 2차원 해석 시 감쇠계수가 과도하게 크게 산출되는 현상을 해결하기 위한 방법으로 보정계수 적용 방법을 검토하였으며 3차원 해석 시 발생할 수 있는 배수량의 변화를 고려하기 위해 2자유도(횡동요, 상하동요)를 고려한 자유 횡동요에 관한 연구를 수행 하였다. Jung et al. [8]은 Jung et al. [6]의 실험결과와 2차원 수치 시뮬레이션 결과를 비교하여 해석 기법의 검증을 수행하였다. Heo et al. [9]는 CFD의 활용 가능성을 검토하기 위해 2차원 문풀에 대한 수치 시뮬레이션을 수행하여 그 결과를 실험 및 선형 포텐셜 이론과 비교하였다. 또한 Wilson et al. [10]과 Park et al. [11]은 CFDSHIP-IOWA를 이용하여 3차원적 방법으로 다양한 속도조건에서 빌지킬 유무에 따른 선박의 자유 횡동요 실험에 대한 수치 시뮬레이션을 수행하여 실험과 비교 분석을 통한 적용 가능성을 확인하였으며, Araki et al. [12]는 중첩격자계 방법을 이용한 수치 시뮬레이션을 적용하기 위해 격자수에 따른 비교 및 자유 횡동요 감멸곡선을 통한 선박의 자유 횡동요 수치 시뮬레이션을 실험 결과와 비교 검증하였다.
본 연구에서는 일반적으로 실험적 방법을 통해 산출되는 횡동요 감쇠계수를 대체하기 위한 연구로 일정 속도로 항주하는 110m급 해양작업지원선의 빌지킬 부착 유무에 따른 자유 횡동요 수치 시뮬레이션을 수행하였으며, 또한 수치 시뮬레이션으로 산출된 각각의 무차원 감쇠 계수를 바탕으로 상용 운동해석 소프트웨어인 MMA(Maxsurf motions advance)를 이용하여 빌지킬 유무에 따른 선박의 운동 해석을 수행하여 횡동요 감소 효과를 연구하였다.
2. 횡동요 감쇠계수
선박은 3가지 병진운동(Surge, Sway, Heave)과 3가지 회전운동(Roll, Pitch, Yaw)의 6자유도 운동을 하며, 일반적으로 선박의 폭이 길이에 비해 짧기 때문에 선박의 안정성 측면에서 폭방향 회전운동인 횡동요(Roll)가 종동요(Pitch)에 비해 상대적으로 중요하다. 일반적으로 선박의 횡동요가 생길 경우 선박은 복원력에 의해 기존 상태로 회복되지만 과도한 횡동요가 발생 시 선박은 복원력을 잃어 본래의 위치로 돌아오지 못하고 전복하게 된다. 특히 파라메트릭 횡동요(Parametric rolling)와 같이 일정 조건에서 발생하는 과도한 횡동요로 인해 선박이 전복되는 등 사고가 발생할 수 있으며, IMO(International Maritime Organization) 보고서에 의하면 1998년 북태평양을 항해 중이었던 Post-Panamax급 컨테이너선에 최대 35~40도의 횡동요가 발생하여 약 800개의 컨테이너가 유실 또는 손상되었으며, 2003년에는 북대서양을 항해 중이었던 PCTC(Pure car truck carrier) 선박에 최대 횡동요가 50도까지 나타났다고 한다[13][14]. 이런 선박의 횡동요를 줄이기 위해 다양한 방법들이 제안되고 있으며, 대표적인 방법으로 선체에 빌지킬을 부착하는 방법과 선내에 설치된 탱크에 물을 넣어 선체의 동요와 물의 이동간의 위상차를 이용하는 감요수조(Anti-rolling tank, ART)를 이용하는 방법이 있다.
선박의 횡동요는 식 (1)과 같이 나타낼 수 있으며, 포텐셜 이론을 이용한 운동 성능 해석은 빌지킬 등과 같은 부가물을 직접적으로 반영하여 해석하기 보다는 횡동요 감쇠계수(Damping coefficient)를 이용하여 부가물의 영향을 고려하기 때문에 정확한 감쇠계수 추정이 중요하며 일반적으로 실험을 통해 얻어진 수치나 경험치 등을 이용한다.
| (1) |
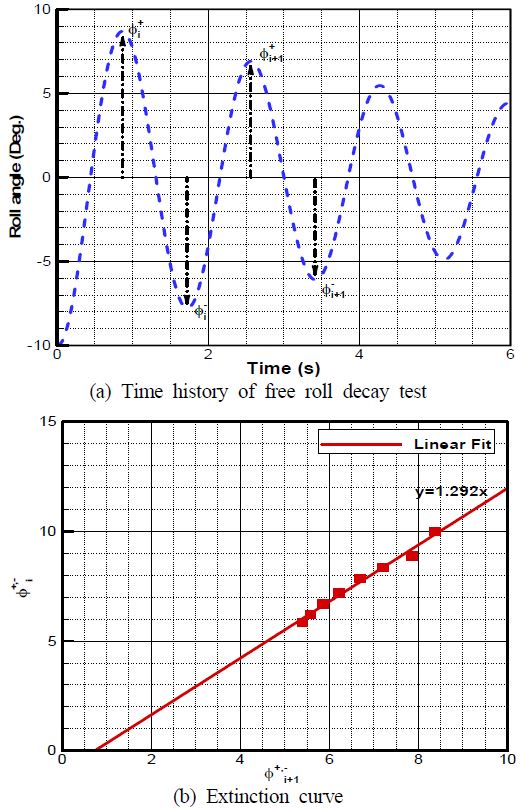
이 때 I는 질량관성모멘트, A는 부가질량관성모멘트, B44는 감쇠계수, C는 복원력계수, F(t)는 외력, 는 가속도, 는 속도, φ는 변위, 하첨자 44는 횡동요를 나타낸다. 본 연구에서 운동해석을 위해 사용하는 MMA에서는 I44=∇ρ, A44는 Vugts [15], Lloyd [16]에서 제시된 값들의 평균값인 0.3I44, C44=GMt∇ρg 그리고 B44는 자유 횡동요 실험을 통해 식 (2), 식 (3)과 같이 계산되어 진다. 이 때 kxx는 횡동요 관성반경, ∇는 배수용적, ρ는 밀도, g는 중력가속도, GMt는 횡방향 경심높이, β44는 무차원 횡동요 감쇠 계수 그리고 Grad는 Figure 2 (b)와 같이 선형 근사한 그래프의 기울기이다.
| (2) |
| (3) |
실험을 통한 감쇠계수 산출은 선박을 초기 횡경사 각도까지 강제로 기울인 뒤 외력을 가하지 않고 자유롭게 운동하도록 하는 자유 횡동요 감쇠실험을 통해 산출된다. 이 때 측정되는 결과는 Figure 2 (a)과 같이 시간에 따른 횡동요량이며 각 주기의 양의 극값()과 음의 극값()의 양쪽 극값을 이용하는 방법 등을 통해 감쇠 계수를 산출 할 수 있다[4].
3. 수치 시뮬레이션 방법 및 조건
3.1 수치 시뮬레이션 방법
본 연구에 이용된 지배방정식은 식 (4) 와 식 (5)와 같이 연속 방정식과 RaNS(Reynold-averaged Navier-Stokes) 방정식으로 비정상, 비압축성 및 점성 유동을 가정하였다. 여기서 U는 평균속도벡터, x는 좌표계, t는 시간, p는 압력, μ는 점성계수, 는 난류전단응력으로 난류모델에 의해 결정되며 B는 체적력이다. 본 연구에서는 점성의 영향이 상대적으로 큰 선박의 횡동요를 고려하기 위해 경계층 내부유동은 k-ω 난류모델을, 경계층 외부유동은 k-ϵ 난류모델을 이용하는 SST k-ω 난류모델을 이용하였다. 또한 본 연구에서는 부유체의 횡동요를 고려하기 위해 식 (6)과 같이 각운동량 방정식을 고려하였다. 이 때 은 부유체에 작용하는 모멘트의 합이며 는 회전축에 대한 각속도이다.
| (4) |
| (5) |
| (6) |
상술한 지배방정식은 유한체적법(Finite-volume method, FVM)에 의해 이산화되며 확산항 및 대류항은 2차 상류차분법(Upwind)이 각각 적용되었으며, 압력과 속도의 연성(Pressure-velocity coupled)에는 SIMPLE-type 알고리즘이 적용되었다.
3.2 초기 조건 및 경계 조건
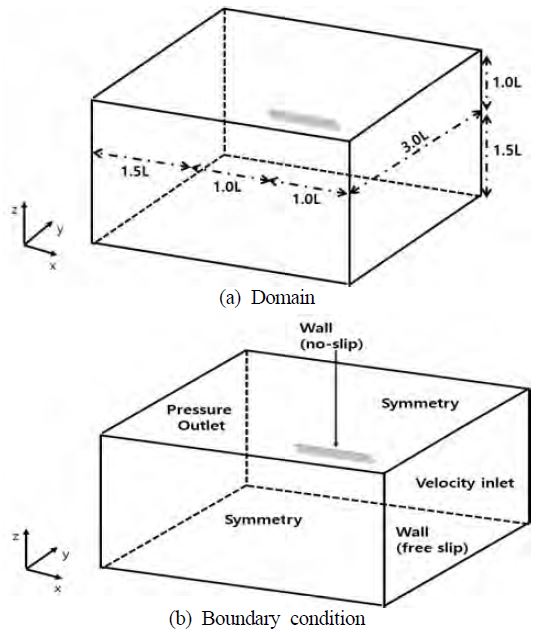
수치 시뮬레이션을 위한 계산영역은 Figure 3 (a)와 같이 길이 방향 3.5L, 폭 방향 3.0L 그리고 높이 방향 2.5L로 설정하였으며, 이 때 L은 수선간장(LBP) 으로 무차원화된 길이이다. 각 영역의 경계조건은 Figure 3 (b)와 같이 상용 소프트웨어에서 이용 가능한 조건들로, 유동이 유입되는 입구경계에는 속도유입조건인 Velocity inlet 조건을, 반대편 출구경계에는 유동이 빠져 나갈 수 있도록 유출조건인 Pressure outlet 조건을, 좌우면은 대칭조건인 Symmetry 조건을, 선박은 벽 경계조건인 Wall(No-slip) 조건 그리고 나머지 부분은 벽 경계 조건인 Wall(Free-slip)을 이용하였다.
수치 시뮬레이션은 비정상상태로 시간에 대해 2차 정확도의 음해법을 적용하였으며, 일정한 속도로 항주하는 선박의 횡동요로 인해 발생할 것으로 예상되는 수면파를 고려하기 위해 2차 정확도의 HRIC(high resoilution interface capturing) 알고리즘을 적용한 VOF(Volume-of-fluid) 방법을 이용하였다. 또한 중첩 격자계(Overset grid)를 사용함에 따라 외부격자와 내부격자간의 물리량 보간은 보다 정확도가 높다고 알려진 최소자승법(Least square method)를 이용하였다.
본 연구에서는 먼저, 해양작업지원선의 수치 시뮬레이션에 앞서 설정된 시뮬레이션 조건을 확인하기 위해 Figure 4에 나타낸 DTMB-5512 모델을 이용하여 실험과 비교를 통한 검증을 수행하였다. 이 때 이용된 DTMB-5512 모델은 DTMB-5415 모델과 동일한 선형에 축척비가 상이한 선형으로 상세 제원은 Table 1과 같으며, 시간증분량(1.0E-2s, 5.0E-3s, 1.0E-3s, 5.0E-4s)과 시간증분량 당 반복 횟수(5, 10, 15, 20)의 각각 4가지 조건에 대하여 수치 시뮬레이션을 수행하여 최적의 조건을 결정하였다.
수치 시뮬레이션에 이용되는 해양작업지원선의 빌지킬의 유무에 따른 형상은 Figure 5에 보이는 바와 같으며, 1:32의 축척비로 상사된 모형선 크기를 이용하였다. 이때 상세 제원은 Table 2에 정리하였다.
3.3 격자계
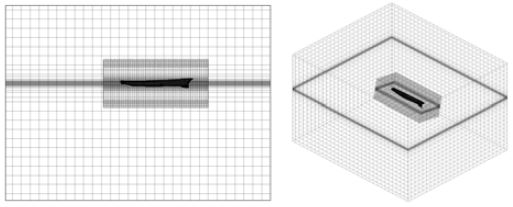
수치 시뮬레이션을 위한 격자계는 자동격자생성 방법(Surface Remesher, Prism Layer, Trimmer)을 이용하여 격자를 생성하였으며, 선박의 횡경사에 따른 운동을 표현하기 위해 중첩 격자 방법을 적용하였다. 이 방법은 수치 시뮬레이션의 제어 체적(Control volume) 전체를 움직이는 것이 아닌 지정된 영역(Overset area)만을 움직여 계산하는 방법으로 고정되어 있는 외부격자 혹은 배경격자(Background grid)와 움직이는 영역인 내부의 중첩 격자로 구성되어 서로 다른 2가지 격자계가 제어 체적 내에 존재하게 된다. 중첩 격자의 영역은 선박의 각 방향으로 0.2L으로 설정하였으며, 선체 주위의 점성 유동장의 경우 표면의 법선방향으로 4개의 layer를 별도로 생성하여 고려하였으며, 자유표면의 경우 자유표면 부근에 추가적으로 격자를 조밀하게 배치하여 VOF 함수의 수치적 확산에 의한 정확도를 확보할 수 있도록 조정하였다. DTMB-5512 선형의 경우 수치 시뮬레이션에 이용된 격자계는 Figure 6과 같이 중첩 격자가 약 60만개, 배경 격자가 약 10만개로 총 약 70만개의 격자가 사용되었으며, 해양작업지원선은 중첩 격자가 약 80만개, 배경 격자가 약 10만개로 총 약 90만개의 격자가 사용되었다.
4. 수치 시뮬레이션 결과
4.1 수치 시뮬레이션 조건 평가
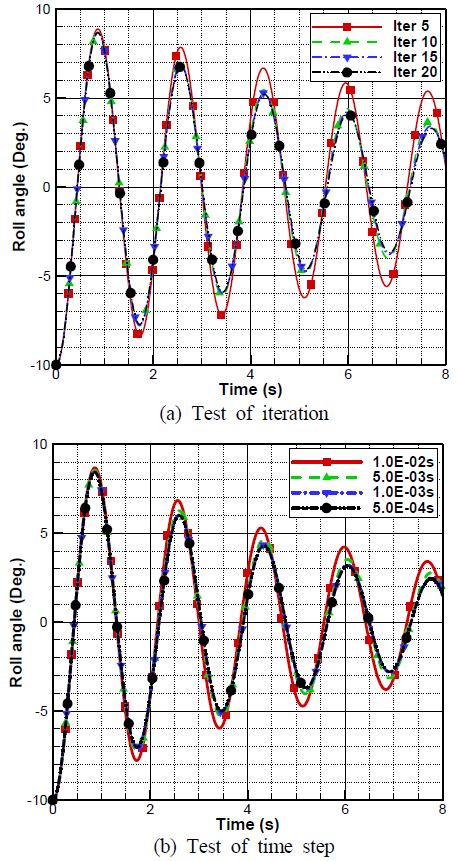
3.2절에서 전술한 바와 같이 해양작업지원선의 수치 시뮬레이션에 앞서 수치 시뮬레이션 조건을 검증하기 위해 DTMB 5512 선형을 이용하여 시간증분량 당 계산 횟수와 시간 증분량에 대한 검증을 수행하였으며, 그 결과는 Figure 7과 같다. 이 때 시간증분량 당 계산횟수 테스트의 시간 증분량은 0.01s이다.
시간증분량 당 반복 계산횟수의 경우 Figure 7 (a)과 같이 계산 횟수가 증가함에 따라 첫 번째 음의 극치 값부터 횡동요 감쇠량의 차이가 발생하고 있으며, 주기가 증가할수록 감쇠량의 차이가 증가한다. 하지만 계산 횟수가 10번부터는 점차 수렴해가는 경향을 보이며, 15번과 20번의 경우 차이가 미미하다. 다만, 각각의 양과 음의 극치가 나타나는 횡동요 주기는 반복 계산횟수에 대한 영향이 없이 일정하게 나타나고 있다. 따라서 시간증분량 당 계산 횟수는 수치 시뮬레이션 계산 시간을 고려할 때 15번이 가장 적합하다고 판단되며, 추후 수행되는 수치 시뮬레이션에 15번의 반복 계산횟수를 적용하였다. 시간 증분량 테스트의 경우, Figure 7 (b)에 보이는 바와 같이, 반복 계산횟수 테스트와 동일하게 시간 증분량이 작아짐에 따라 횡동요 주기는 크게 변화가 없이 일정한 경향을 보이지만, 극치값의 경우 주기가 반복될수록 차이가 증가하고 있다. 하지만 시간 증분량이 5.0E-03s부터는 시간 감소량에 따른 상대 오차가 줄어들며 점차 수렴하고 있으며, 1.0E-03s 와 5.0E-04s의 차이는 무시 가능할 정도로 미미하다. 따라서 시간증분량의 경우 1.0E-03s를 추후 수행되는 수치 시뮬레이션에 적용하였다.
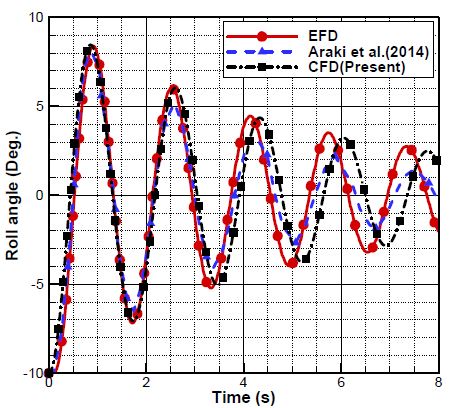
전술한 테스트를 통한 얻어진 시간증분량 당 반복 계산횟수와 시간 증분량 조건들을 적용하여 수치 시뮬레이션을 수행하였으며 그 결과를 실험 및 Araki et al. [12]의 수치 시뮬레이션과 상호 비교를 통해 본 연구에서 수행한 수치 시뮬레이션의 정확도를 확인하였다. 그 결과 Figure 8과 같이 각각의 극치 값은 실험과 수치 시뮬레이션이 정량적으로 유사한 결과를 보이고 있으며, Araki et al. [12]의 수치 시뮬레이션 결과에 비해 상대적으로 향상된 결과를 확인 할 수 있다. 다만 횡동요 주기의 경우 감쇠운동이 반복 될수록 수치 시뮬레이션이 상대적으로 횡동요 주기가 길어져 실험과 차이가 발생하고 있다. 이런 주기의 차이는 본 연구에 이용된 실험이 유속이 없는 정수중에서 수행되는 일반적인 자유 횡동요 실험과 달리 선박의 속도가 고려된 상태에서 수행된 실험이기 때문에 모형실험 시 모형선의 횡동요를 제외한 선박의 움직임을 완전히 구속하는데 어려움이 있어 6 자유도 모든 운동에 대하여 동요량이 발생하였지만, 수치 시뮬레이션에서는 횡동요만을 고려함으로써 발생하는 오차라 사료된다. 또한 수치 시뮬레이션에 사용된 유속조건은 실험 계측시간 동안 측정된 평균값이기 때문에 이로 인해 발생할 수 있는 오차도 포함하고 있을 것이다[17].
4.2 해양작업지원선 수치 시뮬레이션
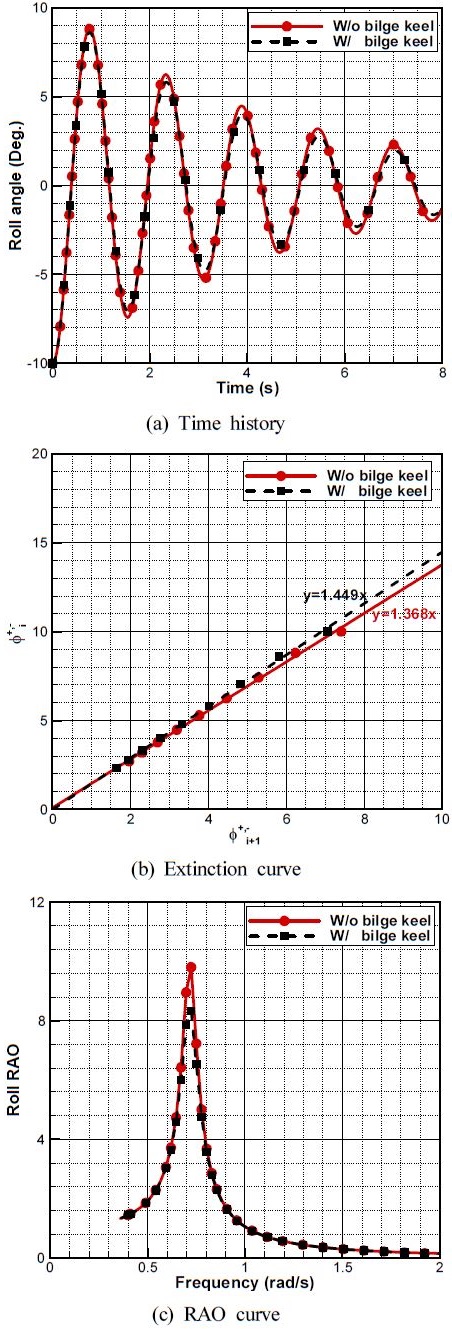
4.1절에서 DTMB 모델을 이용한 수치 시뮬레이션으로 결정된 조건들을 이용하여 해양작업지원선의 자유 횡동요 수치 시뮬레이션을 수행하였다. 그 결과 Figure 9 (a)와 같이 빌지킬이 있는 경우와 빌지킬이 없는 경우 극치 값이 나타나는 주기는 큰 차이가 없지만 횡동요량은 첫 번째 음의 극치부터 차이가 발생하여 각 주기마다 차이가 나타나고 있다. Figure 9 (b)와 같이 각각의 극치값을 이용하여 기울기를 선형 근사(Linear fitting)할 경우 그래프의 기울기는 각각 1.449와 1.368로 계산되며, 식 (2)에 사용될 무차원 횡동요 감쇠계수는 빌지킬이 없는 경우 0.050, 빌지킬이 있는 경우 0.059으로 산출된다.
이후, 산출된 각각의 무차원 감쇠 계수를 이용하여 MMA를 이용한 선박의 운동 해석을 수행하였다. 단 이 때 MMA에서는 2D 스트립 방법을 이용하였으며 일반적으로 횡동요가 가장 크게 나타나는 파향이 선체와 수직인 방향에 대한 해석을 수행하였다. MMA를 이용한 해석 결과 Figure 9 (c)와 같이 선체에 빌지킬이 부착된 경우 횡동요의 응답진폭함수(Response Amplitude Operator)의 극치값이 약 15%가량 감소되는 것을 알 수 있다.
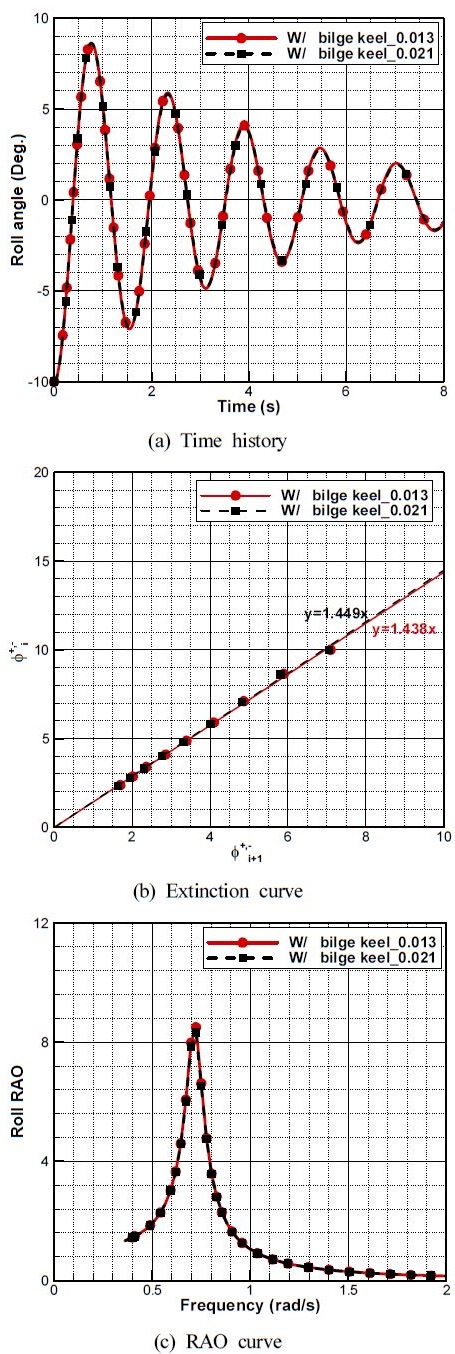
하지만 선체에 부착된 빌지킬의 경우 횡동요 성능 측면에서는 효과가 있지만 저항 측면에서는 저항을 증가시키는 부가물로 그 크기가 작을수록 저항성능이 우수하다. 따라서 효율적인 빌지킬 크기 선정을 위해서는 빌지킬 크기에 따른 운동성능과 저항성능을 모두 고려할 필요가 있으며, 이를 위해 추가적으로 빌지킬의 Height/Breadth 비가 약 40% 작은 0.013에 대하여 수치 시뮬레이션을 수행하였다. 그 결과는 Figure 10과 같이 자유 횡동요 수치 시뮬레이션의 경우 각 주기의 극치 값의 차이는 크지 않으며, 이를 이용해 산출된 무차원 감쇠 계수를 이용한 운동 해석 결과 Table 3에 정리된 것과 같이 응답진폭함수의 극치 값이 빌지킬의 Height/Breadth 가 0.021일 때와 비교하여 약 1.7% 감소하였다. 이 때, 저항성능의 경우 Table 4와 같이 빌지킬이 짧은 경우 총 저항 계수가 0.26% 감소하였고, 이 수치는 ITTC에서 선체의 침수표면적(S)과 빌지킬의 침수표면적(SBK)의 비로 빌지킬의 저항 성능(Rbilge)을 고려하기 위해 제안한 식 (7)을 이용해 산출된 계산결과인 0.27%와 유사한 결과를 보인다.
| (7) |
5. 결 론
본 연구에서는 일정한 속도로 항주하는 해양작업지원선의 빌지킬 유무에 따른 횡동요 운동성능에 대한 연구로 통상적으로 실험적 방법으로 산출되는 무차원 횡동요 감쇠 계수를 대체하기 위한 방법으로 상용 점성유동 해석 프로그램인 Star-CCM+를 이용하여 자유 횡동요 수치 시뮬레이션을 수행하였으며, 이를 통해 횡동요 무차원 감쇠 계수를 추정하였다. 또한 산출된 감쇠 계수를 이용하여 2차원 스트립 이론을 이용한 운동 해석을 통해 빌지킬 유무에 따른 선박의 횡동요 운동 성능 차이를 검토하였다. 단, 운동 해석의 경우 일반적으로 횡동요가 가장 크게 나타나는 파향이 90도인 경우에 대한 시뮬레이션을 수행하였다.
해양작업지원선의 빌지킬 유무에 따른 수치 시뮬레이션의 경우 빌지킬 유무에 따라 횡동요 응답진폭함수의 극치값이 약 15% 차이를 보이며, 이를 통해 빌지킬이 횡동요 성능에 미치는 정량적 효과를 확인할 수 있었다. 또한 선체에 부착되는 빌지킬의 크기에 따른 횡동요 성능을 파악하기 위해 빌지킬 크기를 변경하여 추가적인 수치 시뮬레이션을 수행하여 그 차이를 파악하였으며, 그 결과 빌지킬의 크기를 약 40% 감소시켰을 때 극치값의 차이는 1.7% 내외로 차이가 크지 않아 줄어든 크기에 비해 상대적으로 운동성능의 효과가 적지 않은 것으로 확인되었다. 또한 이 때 수치 시뮬레이션과 ITTC 계산방법에 따른 저항 감소율은 서로 유사한 결과를 나타내며, 빌지킬이 짧은 경우 약 0.3% 저항성능이 우수하다.
본 연구를 통해 서론에 전술한 바와 같이 빌지킬 유무에 따른 선박의 횡동요 운동성능을 파악하기 위기 위하여 일반적으로 실험적 방법을 통해 산출되는 횡동요 감쇠계수를 CFD를 이용한 수치적 방법으로 대체하였으며, 이에 따른 적용가능성을 확인 할 수 있었다. 하지만 본 연구에서 실험과 차이를 보였던 횡동요 주기의 경우는 추가적인 연구를 통한 검증이 필요할 것이며, 이를 바탕으로 추후 다양한 선박의 운동 해석에 적용될 수 있을 것으로 사료된다.
Acknowledgments
본 연구는 2015년도 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다(No. 20153030024010).
References
- Opinet, Available at : http://www.opinet.co.kr Accessed January 5, 2016.
- Y. D. Ha, Offshore Structural Designs and Subsea System, 1st Edition, Seoul, Korea, GSintervision, (2015).
-
K. C. Seo, O. S. Gim, Y. C. Ryu, M. Atlar, and G. W. Lee, “The evaluation of hydrodynamic resistance and motion response characteristics of platform supply vessel”, Journal of the Korean Society of Marine Environment & Safety, vol. 19(no. 4), p397-402, (2013).
[https://doi.org/10.7837/kosomes.2013.19.4.397]

-
N. W. Kim, Y. J. Kim, and Y. R. Ha, “Experimental study of the free roll decay test for the evaluation of roll damping coefficients”, Journal of the Society of Naval Architects of Korea, vol. 52(no. 6), p460-470, (2015).
[https://doi.org/10.3744/SNAK.2015.52.6.460]

-
M. Irvine, J. Longo, and F. Stern, “Forward speed calm water roll decay for surface combatant 5415: Global and local flow measurements”, Journal of Ship Research, vol. 57(no. 4), p202-219, (2013).
[https://doi.org/10.5957/JOSR.57.4.110043]

-
K. H. Jung, S. B. Suh, and H. H. Chun, “Experimental study on the eddy making damping effect at the roll motion of a rectangular barge”, Journal of the Society of Naval Architects of Korea, vol. 44(no. 3), p267-278, (2007).
[https://doi.org/10.3744/SNAK.2007.44.3.267]

- J. H. Bae, C. B. Hong, and H. U. Kwak, “A study on 3D roll damping of a ship by numerical analysis using moving grid”, Proceedings of the The Korean Association of Ocean Science and Technology Societies, p632-640, (2009).
-
J. H. Jung, H. S. Yoon, H. H. Chun, I. W. Lee, and H. Park, “Numerical simulation of wave interacting with a free rolling body”, International Journal of Naval Architecture and Ocean Engineering, vol. 5(no. 3), p333-347, (2013).
[https://doi.org/10.2478/IJNAOE-2013-0137]

-
J. K. Heo, J. C. Park, and M. H. Kim, “CFD analysis of two-dimensional floating body with moon pool under forced heave motion”, Journal of Ocean Engineering and Technology, vol. 25(no. 2), p36-46, (2011).
[https://doi.org/10.5574/KSOE.2011.25.2.036]

-
R. V. Wilson, P. M. Carrica, and F. Stern, “Unsteady RANS method for ship motions with application to roll for a surface combatant”, Computers & fluids, vol. 35(no. 5), p501-524, (2006).
[https://doi.org/10.1016/j.compfluid.2004.12.005]

-
I. R. Park, S. H. S. Hosseini, and F. Stern, “Numerical analysis of ship motions in beam sea using unsteady RANS and overset grid methods”, Journal of the Society of Naval Architects of Korea, vol. 45(no. 2), p109-123, (2008).
[https://doi.org/10.3744/SNAK.2008.45.2.109]

- M. Araki, K. Ohashi, and N. Hirata, “An analysis of bilge keel effects using RANS with overset grids method”, The 14th Inernational Ship Stability Workshop (ISSW), Kuala Lumpur, Malaysia, p216-228, (2014).
- International Maritime Organization(IMO), Sub-committee on Stability and Load Lines and on Fishing Vessels(SLF), Review of the Intact Stavility Code-Head sea parametric rolling and its influence on container lashing systems, Submitted by the United states, SLF 45/6/7, (2002).
- International Maritime Organization(IMO), Sub-committee on Stability and Load Lines and on Fishing Vessels(SLF), Review of the Intact Stavility Code-Recordings of head sea parametric rolling on a PCTC, Submitted by Sweden, 47/INF.5, (2004).
- J. H. Vugts, “The Hydrodynamic Coefficients for Swaying, Heaving and Rolling of Cylinders in a Free Surface”, Netherlands Ship Research Centre TNO Report 112 S, (1968).
- A. R. J. M. Lloyd, Seakeeping: Ship behaviour in rough weather, 2nd Edition, Ellis Horwood Limited, West Sussex, (1998).
- Iowa Institute of Hydraulic Research, (2010), Available at : http://www.iihr.uiowa.edu/shiphydro/efd-data/5512-roll-decay Accessed January 2016.