[ Original Paper ]

Journal of the Korean Society of Marine Engineering - Vol. 40, No. 9, pp.786-790

ISSN: 2234-7925 (Print) 2234-8352 (Online)

Print publication date Nov 2016

Received 14 Jul 2016 Revised 02 Sep 2016 Accepted 11 Nov 2016

DOI: https://doi.org/10.5916/jkosme.2016.40.9.786

자연대류 냉각되는 경량고성능 할로우 하이브리드 휜 히트싱크의 열성능에 대한 방향 영향의 전산연구

니코 스띠아완 에벤디¹ ; 김경준^†

Computational study of orientation effects on thermal performance of natural convection cooled lightweight high performance hollow hybrid fin heat sinks

Nico Setiawan Effendi¹ ; Kyoung-Joon Kim^†

1Department of Mechanical Design Engineering, Pukyong National University, Tel: 051-629-6168 nicose1609@gmail.com

Correspondence to: ^†Department of Mechanical Design Engineering, Pukyong National University, 365 Sinseon-ro, Nam-gu, Busan, 48547, Korea, E-mail: kjkim@pknu.ac.kr, Tel: 051-629-6168

Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록

본 연구는 자연대류상의 할로우 하이브리드 휜 히트싱크 (HHFHS) 의 열성능에 대한 방향 영향의 전산연구결과에 대해 논한다. HHFHS 는 휜 베이스 근처에 천공을 포함하는 중공 핀 휜과 판 휜의 결합형 휜들의 배열로 구성된다. HHFHS 의 베이스면적기반, 질량기반 열성능에 대한 방향영향이 0 ~ 180도의 방향각에 대해서 수치적으로 연구되었고, 유사구조의 핀 휜 히트싱크 (PFHS) 와 비교되었다. PFHS 와 달리 HHFHS 의 열저항은 직립상태에서 45도까지 변화가 미미하며, 이후 증가하여 90도에서 최대이며, 이후로는 180도까지 감소함을 보인다. 이러한 열저항 특성의 차이는 HHFHS의 중공 휜의 내부유동에 의한 열펌핑 효과의 영향으로 사료된다. 다양한 방향각에도 HHFHS 의 질량기반 열저항은 약 30% 정도 PFHS 보다 작음을 보여주는데 이 결과는 자연대류 상의 전자장치에 대한 HHFHS 의 경량열관리 적용 가능성을 보여준다.

Abstract

This paper discusses numerically explored orientation effects on the thermal performance of hollow hybrid fin heat sinks (HHFHSs) under natural convection. A HHFHS consists of an array of hollow pin fins concatenated with plate fins and having perforations near the fin bases. Orientation effects on the footprint-based and mass-based thermal performance of the HHFHS were numerically studied for orientation angles ranging from 0° to 180°. The performance of the HHFHS was compared with that of a pin fin heat sink (PFHS) having similar physical parameters. The results show that the thermal resistance of the HHFHS did not vary considerably from 0° to 45°. The thermal resistance increased from 45° to 90°, reached its maximum at 90°, and decreased consistently from 90° to 180°. Dissimilar behaviors of the thermal resistance of the HHFHS vs. the PFHS resulted mainly from the effect of heat pumping induced by the internal flows of the hollow fins. Despite various orientations, the mass-based thermal resistance of the HHFHS was found to be nearly 30% smaller than that of the PFHS. This result shows the feasibility of the HHFHS for the lightweight thermal management of electronics under natural convection.

Keywords:

Hollow hybrid fin heat sink, Orientation effect, Lightweight thermal management, Natural convection, CFD

키워드:

할로우 하이브리드 휜 히트싱크, 방향영향, 경량열관리, 자연대류, 전산유체역학

1. 서 론

LED 등, remote radio transceiver, 실외 방산용 전자장치와 같이 고에너지효율이 요구되거나 전력망으로부터 고립된 전자 및 광전자장치의 열 및 온도관리에는 자연대류 냉각이 적합하다. 히트싱크는 지속가능하고, 강건하며, 경제적인 자연대류 냉각 해결법이지만, 히트싱크의 무게는 제조비와 열관리되는 시스템의 구조적 안정성에 영향을 주는 주요 변수이다[1][2]. 더불어 자연대류 상의 히트싱크의 성능은 방향에 종속적이다[3].

선행연구에서는 LED 거리등의 냉각을 위해 제안된 관통형 하이브리드 휜 히트싱크 (PHFHS) 의 가능성 연구를 수행하였고[4][5], PHFHS는 내부유로와 관통형 판 휜을 지니는 할로우 핀 휜들로 구성되며, 각 휜 베이스 근처에는 천공이 존재한다[5]. PHFHS는 Elshafei[6]가 연구한 할로우 핀 휜 히트싱크와는 상이한 독창적 구조를 지닌다. 연구된 가능성에도 불구하고, PHFHS는 복잡한 휜 구조로 인해 제조과정이 도전적이다. 따라서 상대적으로 단순한 하이브리드 휜 구조들이 제안 되었고, 열성능이 연구되었으며[7][8], 경량화에 적합한 직립상태의 할로우 하이브리드 휜 히트싱크 (HHFHS)의 열성능도 수치적으로 연구되었다[9]. 본 연구에서는 선행연구에서 수행하지 않았던 HHFHS의 성능에 미치는 방향 영향을 조사한다. 연구 결과를 논하기 위해, 첫째로 HHFHS 의 다양한 방향에 대한 열성능을 조사하기 위해 적용된 전산열유동모델과 모델링 기법에 대해 설명한다. 둘째로 대표적 조건에서 수치적으로 가시화된 HHFHS 의 온도장과 유동장을 핀 휜 히트싱크 (PFHS) 와 상대비교 한다. 마지막으로 HHFHS 의 베이스 면적 대비 열성능과 질량대비 열성능에 대한 방향 영향을 수치적으로 조사한 결과를 제시하고, PFHS 의 결과와 비교하여 물리적 의의를 해석한다.

2. 할로우 하이브리드 휜 히트싱크

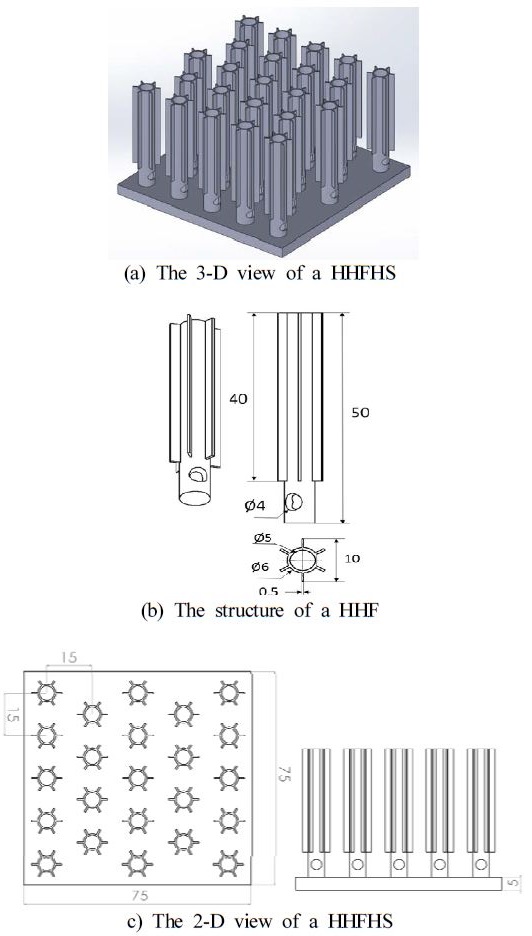
본 연구에서 해석 대상인 HHFHS 의 기준 구조와 수치는 Figure 1에 제시되어 있고, 모든 단위는 mm이다. Figure 1 (b) 에 도식화 되어 있는 것처럼 할로우 하이브리드 휜 (HHF)은 휜 베이스 근처에 천공이 존재하는 중공 핀 휜과 방사형 판 휜의 결합으로 이루어진다. Figure 1 (c)는 HHF의 엇갈림 배열로 구성되는 HHFHS 의 구조를 설명한다.

Figure 1:

The structure of a HHFHS

Figure 1 (b)에 제시되어 있는 것처럼 휜의 총 길이는 50mm, 외경은 6mm, 내경은 5mm, 천공 직경은 4mm 이고, 판 휜의 길이는 40mm, 폭은 2mm이며, 휜 두께는 0.5mm 이다. 휜 공간은 15mm, 히트싱크 베이스 면적은 75mm × 75mm, 베이스 두께는 5mm 이며, 알루미늄이 기본 소재로 선택되었다. 열성능을 상대비교하기 위해 PFHS 가 선택되었고, 이때 휜 길이는 50mm, 직경은 6mm 이며, 베이스 면적과 두께, 휜 공간은 HHFHS 와 동일하며, HHFHS 와 PFHS 의 수치는 다음의 Table 1에 잘 비교되어 있다.

Table 1:

Dimensions (mm) of the HHFHS and the PFHS

3. 열유동모델

HHFHS 와 비교 대상인 PFHS 의 열성능에 미치는 방향영향을 해석하기 위해 3-D 열유동모델이 생성되었다. ANSYS ICEM CFD 를 활용하여 생성된 약 200만개의 격자를 사용하였고, ANSYS FLUENT [10]을 이용하여 열유동장을 계산하였다.

히트싱크의 크기, 표면상태, 휜 공간 등의 기하학적 조건을 고려하여 모델의 자연대류유동에 대해 정상, 비압축성 유동 조건과, Boussinesq 간략화가 선택되었다.

계산격자와 공기영역의 크기가 히트싱크 열저항에 미치는 영향을 상세히 고찰하여 모델의 격자독립성과 공기영역크기에 대한 독립성을 검증하였고, 이는 수치해석 결과의 신뢰도를 정성적으로 보증한다.

열유동장 해석에 대한 지배방정식은 다음의 식 (1)-(5)에 제시되어 있다. 여기에서 식 (1)은 연속방정식, 식 (2)-(4)는 운동량방정식, 식 (5)는 에너지 방정식이다[11].

∂ u ∂ x + ∂ υ ∂ y + ∂ w ∂ z = 0

(1)

u ∂ u ∂ x + υ ∂ u ∂ y + w ∂ u ∂ z = - 1 ρ ∂ P ∂ x + ν ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 + ∂ 2 u ∂ z 2

(2)

u ∂ υ ∂ x + υ ∂ υ ∂ y + w ∂ υ ∂ z = - 1 ρ ∂ P ∂ y + ν ∂ 2 υ ∂ x 2 + ∂ 2 υ ∂ y 2 + ∂ 2 υ ∂ z 2

(3)

u ∂ w ∂ x + υ ∂ w ∂ y + w ∂ w ∂ z = - 1 ρ ∂ P ∂ y + ν ∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2 + ∂ 2 w ∂ z 2 + gβ T - T ∞

(4)

u ∂ T ∂ x + υ ∂ T ∂ y + w ∂ T ∂ z = α ∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 + ∂ 2 T ∂ z 2

(5)

여기에서 u, v, w 는 각각 x, y, z 방향의 속도 (m/s), ρ는 밀도(kg/m³), P 는 압력(Pa), ν는 점성계수 (m²/s), g는 중력가속도(m/s²), β는 체적열팽창계수(1/K), T는 온도(K), T_∞ 는 주변 유체 온도(K), α는 열확산율 (m²/s)이다.

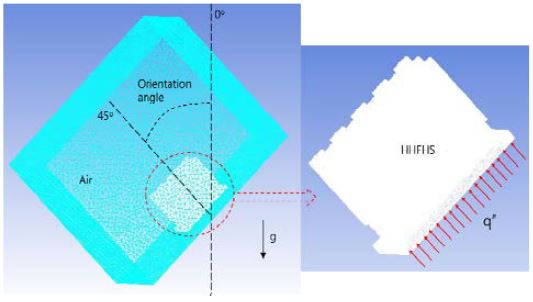
Figure 2는 HHFHS의 열유동모델과 경계조건을 제시하는데, 베이스 아랫면에 균일한 열유속 부하가 설정되었고, 주변공기온도는 25°C의 실온으로 가정되었다. HHFHS의 소재는 히트싱크 소재로 광범위하게 사용되는 알루미늄으로 설정되었다.

Figure 2:

The CFD model and boundary conditions of a HHFHS

4. 열특성

본 장에서는 0 ~ 180 도의 방향각에 대해서 열유동모델에 의해 해석된 엇갈림 배열과 정열배열 HHFHS 와 PFHS 의 footprint 기반과 질량기반 열성능을 논한다.

히트싱크의 열성능 지표로 footprint 기반 열저항, R_th, 질량기반 열저항, R_th M 을 정의하였으며, 다음의 식으로 표현된다.

R th = T b - T a q

(6)

R th M = T b - T a M q

(7)

여기서 q는 히트싱크 베이스에 공급되는 총 열전달률(W), T_b는 히트싱크 베이스의 평균 온도(℃), T_a는 주변의 공기온도(℃), M은 히트싱크의 질량이다.

4.1 온도장과 유동장

본 절에서는 전산모사된 HHFHS, PFHS의 대표적 온도장과 유동장을 가시화하여 해석의 정성적 합리성을 확인하고, 대표적인 온도장과 유동장 특성을 이해함이 주목적이다.

온도장과 유동장을 대표적으로 가시화하기 위하여 15mm 휜 공간, 30W 열소산, 45도 방향각에서의 결과를 Figure 3과 Figure 4에서 제시한다.

Figure 3:

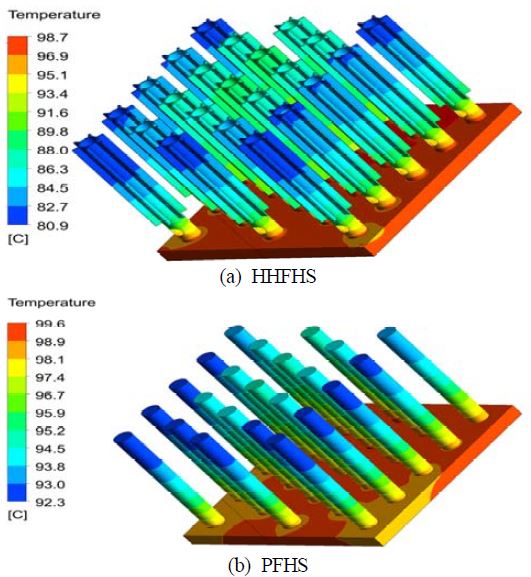
Temperature fields of a HHFHS and a PFHS with a heat dissipation of 30W at an orientation angle of 45°

Figure 4:

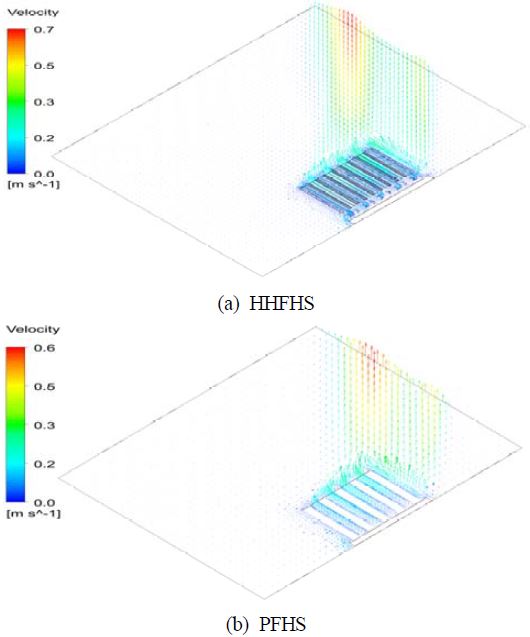
Air velocity fields of a HHFHS and a PFHS with a heat dissipation of 30W at an orientation angle of 45°

가시화된 휜 온도구배, 히트싱크 베이스에서 온도 분포의 대칭성과 에지 (edge) 효과, 유동의 속도분포는 해석결과의 정성적 합리성을 설명한다.

온도장 해석결과는 HHFHS가 PFHS 보다 평균 베이스 온도가 약간 낮음을 보이고, 유동장 해석결과에 의하면 HHFHS의 유로를 통한 내부유동이 거의 0.1m/s의 속도로 원활함을 알 수 있다.

4.2 방향 영향

본 절에서는 HHFHS와 PFHS 의 열성능에 미치는 방향영향에 대해서 논한다. Figure 5는 히트싱크 footprint 기반 열특성, Figure 6은 히트싱크 질량기반 열특성에 대한 방향영향 결과를 제공한다.

Figure 5:

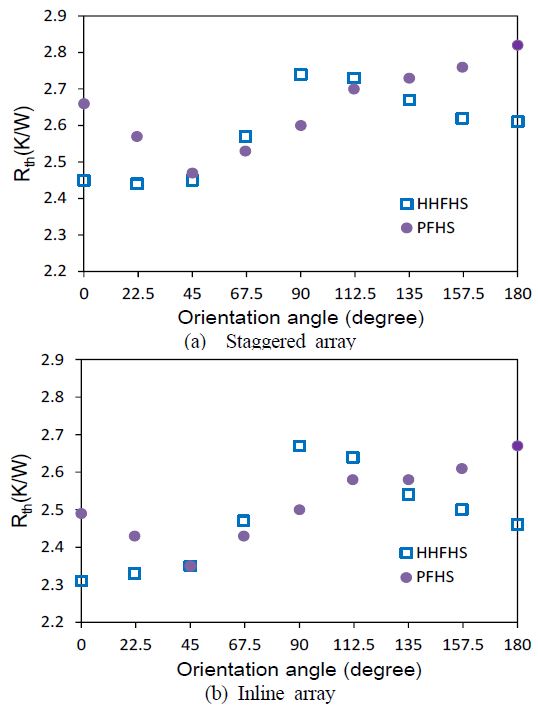
Footprint-based thermal performances of staggered and inline HHFHSs and PFHSs as a function of orientation angle at 30W

Figure 5 와 Figure 6 에서 각각 (a)는 엇갈림배열 (b)는 정렬배열 경우의 결과이며 이때 열소산은 30W 이다. 해석 결과는 PFHS 에서 두 배열 모두 방향각이 45도 일 때 열저항이 최소이고, 45도 이후로 열저항이 증가함을 보인다. 반면에 HHFHS 경우는 방향각 45도 이후로 열저항이 급격하게 증가하여 90도에서 최대값을 지니고, 그 이후로 감소함을 보인다.

Figure 6:

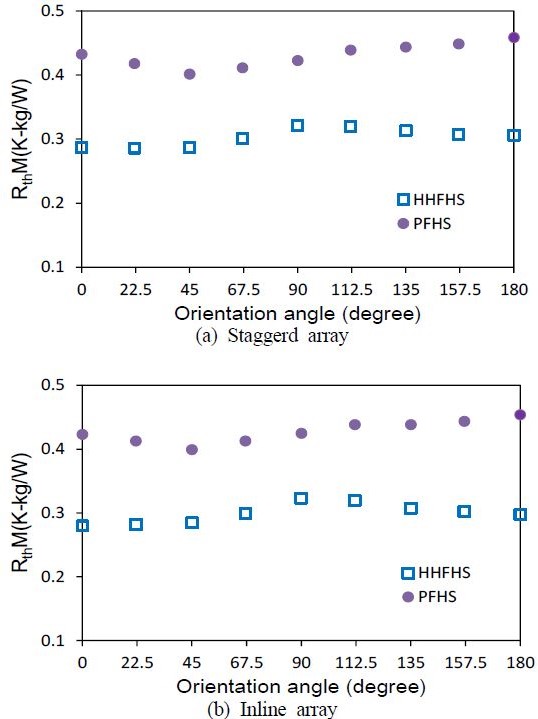
Mass-based thermal performances of staggered and inline HHFHSs and PFHSs as a function of orientation angle at 30W

방향각이 0도인 직립상황에서 45도까지 열저항 값이 뚜렷한 감소를 보이는 PFHS 와 상이하게 HHFHS 열저항 값의 변화는 미미하다. 이러한 결과는 방향각의 증가에 의한 중공 휜 내부유동의 약화에 기인하는 내부 열펌핑 효과의 감소가 외부 유동에 의한 열전달 증가를 감쇄시키기 때문으로 해석이 가능하다. 방향각 90도에서 180도까지 열저항 값이 증가하는 PFHS 와 상반되게 HHFHS 열저항 값은 감소하는데, 이는 방향각의 증가에 따라 내부유동의 활성화에 의한 내부 열전달 효과의 증가에 기인한 것으로 보인다.

Figure 6 에 제시된 것처럼, PFHS 대비 HHFHS의 질량기반 열저항은 약 30% 정도 작다. 이 결과는 휜 내부유로에서 내부유동에 의한 열펌핑 효과와 휜 내부공간에 의한 무게 감소에 기인한다. PFHS 와 HHFHS 의 질량기반 열저항 프로파일의 차이는 각 히트싱크의 열저항 프로파일의 차이와 유사하고 기 언급한 물리적인 이유로 설명할 수 있다.

엇갈림배열과 정렬배열의 열저항 프로파일은 정성적으로 매우 유사한 흥미로운 결과를 제시한다. 이 결과는 각 배열의 휜 공간이 동일하기 때문으로 보인다. 하지만 열저항 결과 값은 정렬배열의 경우가 엇갈림배열 대비 다소 작음을 보인다. 정렬배열 히트싱크의 휜 수가 엇갈림배열 히트싱크의 휜 수보다 더 많기 때문에 정렬배열 경우의 휜 표면적이 약 17% 더 넓다. 배열에 따르는 열저항 차는 이러한 휜 표면적 차이에 기인한다.

5. 결 론

본 연구에서는 할로우 하이브리드 휜 히트싱크 (HHFHS)의 열성능에 대한 방향영향의 연구결과에 대해 논한다. HHF는 방사형으로 위치한 판 휜을 지니는 중공 핀 휜이며, 휜 베이스에는 천공이 존재하고, HHFHS는 HHF 의 배열로 구성된다. 본 연구에서 3차원 CFD 모델을 적용하여 0 ~ 180도의 방향각에 대해서 수치연구를 수행하여 베이스면적기반 열성능과 질량기반 열성능에 대한 HHFHS 의 방향 영향을 조사하였고, 열성능에 대한 방향 영향을 상대비교하기 위해 PFHS에 대한 수치연구도 병행되었다. 휜 배열의 영향도 조사하기 위해 동일한 휜 공간에 대해서 엇갈림배열과 정렬배열상의 HHFHS 와 PFHS 의 열성능도 해석되었다.

본 연구에서는 다음의 흥미로운 연구결과가 도출되었다. PFHS 의 열저항은 방향각 45도에서 최소이며 이후에는 지속적으로 증가함을 보이는데, HHFHS의 열저항은 직립상황에서 45도까지 변화가 미미하며, 이후로 증가하여 90도에서 최대값을 지니며, 그 이후로는 감소함을 보인다. 45도까지 미미하게 변하는 HHFHS의 열저항은 방향각의 증가에 따라 내부 열펌핑 효과가 감소하여 외부 열전달 효과를 상쇄시키게 되어 초래되는 결과로 보인다. 또한, 방향각 90도에서 180 도까지 HHFHS 열저항의 감소는 방향각의 증가에 따라 내부 열펌핑 효과가 증가하기 때문으로 해석된다. PFHS 대비 HHFHS의 질량기반 열저항은 약 30% 정도 작은데 이는 내부 열펌핑 효과와 중공에 의한 무게 감소에 기인한다. 엇갈림배열과 정렬배열상의 각 히트싱크의 열저항 프로파일은 정성적 유사성을 보이는데 이 결과는 동일한 휜 공간에 기인한 것으로 보인다.

Acknowledgments

이 논문은 부경대학교 자율창의학술연구비(2015년)에 의하여 연구되었음.

References

K. J. Kim, “Numerically-investigated thermal performances of hybrid fin heat sinks for lightweight thermal management of LED modules under natural convection”, Journal of the Korean Society of Marine Engineering, vol. 39(no. 6), p586-591, (2015), (in Korean). [https://doi.org/10.5916/jkosme.2015.39.6.586]
K. J. Kim, “Numerical study on the thermal behavior of a natural convection hybrid fin heat sink”, Journal of the Korean Society of Marine Engineering, vol. 37(no. 1), p35-39, (2013), (in Korean). [https://doi.org/10.5916/jkosme.2013.37.1.35]
E. M. Sparrow, and S. B. Vemuri, “Orientation effects on natural convection/radiation heat transfer from pin-fin arrays”, International Journal of Heat and Mass Transfer, vol. 29(no. 3), p359-368, (1986). [https://doi.org/10.1016/0017-9310(86)90206-1]
H. Kim, K. J. Kim, and Y. W. Lee, “Thermal performance of smart heat sinks for cooling high power LED modules”, Proceeding of the 13th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronics Systems, p62-67, (2012).
K. J. Kim, “Performance of hybrid fin heat sinks for thermal control of light emitting diode lighting modules”, Journal of Electronic Packaging, vol. 136(no. 1), p011002, (2014).
E. A. M. Elshafei, “Natural convection heat transfer from a heat sink with hollow/perforated circular pin fins”, Energy, vol. 35(no.7), p2870-2877, (2010). [https://doi.org/10.1016/j.energy.2010.03.016]
M. S. Jeon, and K. J. Kim, “Numerical study on the thermal performance of passively cooled hybrid fins”, Journal of the Korean Society of Marine Engineering, vol. 37(no. 8), p816-821, (2013), (in Korean). [https://doi.org/10.5916/jkosme.2013.37.8.816]
K. J. Kim, “Orientation effects on the performance of natural convection cooled hybrid fins”, 20th International Workshop on Thermal Investigations of ICs and Systems, Greenwich, UK, September), (2014. [https://doi.org/10.1109/therminic.2014.6972512]
N. S. Effendi, and K. J. Kim, “Thermal behaviors of passively cooled hybrid fin heat sinks for lightweight and high performance thermal management”, Proceedings of the ASME 2015 InterPACKICNMM, IPACK2015-48630, (2015). [https://doi.org/10.1115/ipack2015-48630]
ANSYS Inc, ANSYS Fluent User’s Guide, (2016).
K. A. Hoffmann, and S. T. Chiang, Computational Fluid Dynamics Volume I, 3rd Ed, Wichita, KS, Engineering Education System, (1998).