축계진동 저감을 위한 동흡진기의 제안
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
선박의 주기관으로 통상 사용되는 디젤기관은 터빈기관과 같은 회전기관과 달리 왕복동기관이기 때문에 실린더의 폭발력과 피스톤의 왕복관성력에 의한 불평형 관성력 및 관성모멘트, 실린더내의 주기적인 변동가스압력 등으로 인하여 본질적인 진동문제를 안고 있다. 이것은 엔진의 진동은 소음의 원인이 되고, 선체구조나 인접구조물에 전달되어 2차진동이 발생시키는 경우가 많다. 본 연구는 선박의 엔진과 축계의 자유진동해석과 엔진 폭발에 의한 강제진동해석을 하고, 나아가서 플라이휠에 부진동 장치인 동흡진기를 설치하여 진동을 줄이는 방법을 제안하고자 한다.
Abstract
Ship’s diesel engines have intrinsic problem to make vibrations caused by cylinder explosion and unbalanced rotating mass. These vibrations might induce noises, are transferred to hull and neighboring structures and cause secondary vibrations. This paper suggests the use of an additional dynamic absorber with a sub-vibration system to reduce the aforementioned vibrations. This dynamic absorber is designed based on an analysis of the free vibration of the engine shafting system and the forced vibrations.
Keywords:
Shaft vibration, Reciprocating rotating inertia, Inertia moment, Dynamic absorber, Sub vibration system키워드:
축계진동, 왕복관성력, 관성모멘트, 동흡진기, 부진동장치1. 서 론
선박의 진동은 선체진동, 기관 및 축계진동, 국부진동으로 크게 나누어진다. 선체진동이 문제가 되어 선체가 절단되는 일은 거의 없고, 또한 국부진동이 선체 강도에 크게 영향을 미치는 일은 없지만 국부적인 진동과 소음을 발생시킨다. 기관 및 축계진동은 기관이나 축계 나아가서는 선체에 치명적인 영향을 미칠 수 있는 중요한 위해 요소이다. 따라서 국제해사기구(IMO)와 각 선급[1][2]에서도 선박의 진동·소음의 문제에 대하여 규칙으로 강제 규정하고 있다. 또 주요 선급에서는 여기에 대한 학술회의[3]도 개최하여 그 중요성을 강조하고 있다. 선박소음은 선체의 강도에는 그다지 큰 영향을 미치지는 않으나 승무원이나 여객에는 심각한 정신적인 피해를 줄 수 있어서 IMO에서는 MSC 부속서에서 세세하게 규정하고 있다[4].
Moon et al. [5]은 비틀림 진동에 의한 선박용 2행정 저속엔진으 크랭크축 파단 현상을 해석한 바 있고, Park et al. [6]은 추진축계 비틀림 진동 감쇠를 위한 점성 댐퍼의 최적 설계에 대하여 연구하였고, Lee et al. [7]은 비틀림진동에 의한 주기관의 진동현상을 연구한 바가 있고, Barro[8] 등은 빙하의 충격 토크 의한 선박용 디젤 엔진 추진축계의 비틀림 진동의 과도응답에 대하여 연구한 바 있다.
축계진동의 고유진동해석은 오랫동안 Holzer 법[9]으로 해석하여 지금도 Holzer 표를 만들어 고유진동수를 구하고 있는데 Holzer 법의 계산 방법의 태생적 문제 때문에 고차의 고유진동수를 계산할 수 없는 단점이 있다. 그래서 저차의 2, 3 개의 고유진동수만을 계산하고 이를 선주에게 제공하고 있다. 행렬을 이용한 고유치 해석법을 이용하면 수학적으로는 거의 오차 없이 해석 자유도만큼의 고유진동수와 고유진동형을 찾을 수 있다.
모델의 정확도만 좋다면 강제진동의 해석도 행렬의 연산에 의하여 정확하게 계산 가능하다.
본 연구에서는 축계진동의 고유진동 해석과 강제진동 해석을 수학적으로 일목요연하게 정리하고, 교과서에 나와 있는 예제 문제에 적용하여 그 실효성을 보이고, 새로운 동흡진기를 제안하여 축계진동의 저감을 실현하고자 한다.
2. 이 론
2.1 1자유도계의 동흡진기
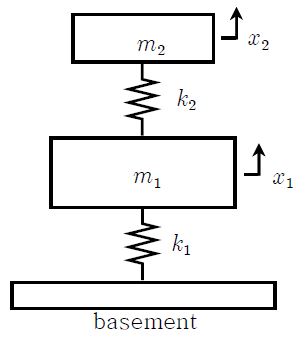
Figure 1에 1자유도 시스템에 동흡진기를 장착한 모형을 보인다. 주 시스템의 질량이 m1이고, 스프링 상수가 k1인 스프링에 의하여 바닥에 고정된 모습이다. 내부에 표시된 시스템은 진동 흡수를 위한 부진동 장치(동흡진기)로 질량이 m2이고 스프링 상수가 k2이다. 이 시스템은 2자유도 시스템이다.
A model of 1 DOF machine system with dynamic absorber
2자유도계의 운동방정식은 다음과 같이 쓸 수 있다.
| (1) |
이 시스템의 해는 다음과 같은 조화함수로 표시할 수 있다.
| (2) |
질량 m1과 m2의 정상상태 진폭을 다음과 같이 구할 수 있다.
| (3) |
우리의 주목적은 시스템의 진폭(X1)을 감소시키는 데에 있다. 질량 m1의 진폭을 0으로 만들기 위해서는 식 (3)의 첫째 식의 분자가 0이 되어야 한다. 즉 다음과 같은 관계를 만족하는 동흡진기를 선택하면 된다.
| (4) |
2.2 축계장치의 고유진동수와 고유진동모드
통상 축계장치의 고유진동수와 고유진동모드는 Holzer법을 쓰고 있으나 Holzer법은 고유진동수를 가정하고, 한쪽 끝단의 고유진동모드를 1로 출발하여 모든 회전체의 관성토크를 합한 값을 구한다. 축계장치는 양단이 자유단이기 때문에 관성토크의 합이 0이 되어야 하지만 가정한 고유진동수가 실제 시스템의 고유진동수가 아니기 때문에 관성토크의 합이 0이 되지 않는다. 그래서 고유진동수를 조금씩 변경시켜 가면서 관성토크의 0이 되는 고유진동수를 찾아가는 방법으로 시간도 많이 걸리고, 각 절점에서의 계산 값이 다음 절점으로 계속하여 승계되기 때문에 오차의 누적이 일어나고, 따라서 실제로 계산을 해보면 관성토크의 합이 0이 되지 않는다.
그러나 운동방정식을 행렬로 표시하여 고유치해석을 하면 거의 0에 수렴시킬 수 있다. 따라서 여기에서는 고유치해석법을 쓰기로 한다.
다자유도 비감쇠운동방정식을 쓰면 다음과 같이 된다.
| (5) |
여기에서 [M]은 질량행렬이고, [K]는 강성행렬이고, {f}는 외력벡터이다. 외력이 없으면 자유진동이 되어 다음과 같은 조화함수 형태의 해가 구해진다.
| (6) |
이것을 식 (5)에 대입하여 정리하면 eiωnt는 0이 될 수 없으므로 이 식은 다음과 같이 되어 일반고유치문제가 된다.
| (7) |
이 고유치문제를 풀면 자유도 수만큼의 고유진동수와 고유진동모드를 구할 수 있다.
2.3 축계장치의 강제진동 해석
여기에서는 다음과 같은 조화력이 작용하는 경우에 대하여서만 생각하기로 한다.
| (8) |
이 시스템은 선형이므로 여러 개의 힘이 작용하여도 이를 따로따로 풀어서 더하면 된다. 따라서 1점에 조화력이 작용하는 경우에 대하여서만 고려하고, 여러 개의 힘이 동시에 작용하는 경우에는 따로따로 계산하여 합하면 된다. 1점에만 힘이 작용하는 경우이므로 {F0}는 한 요소만 F0이고 나머지 요소는 전부 0이다. 그러면 식 2.14는 다음과 같이 된다.
| (9) |
이 운동방정식의 해는 다음과 같다.
| (10) |
이를 식 (9)에 대입하여 정리하면 다음과 같이 된다.
| (11) |
양변을 cosωt로 나누면
| (12) |
따라서
| (13) |
이 되어 해를 구할 수 있다. 여러 개의 힘이 동시에 작용하면 같은 방법으로 구하여 전부 더하면 된다.
3. 선박 축계에의 적용[10]
3.1 축계의 개괄
축계에의 적용은 H. J. Jeon and D. C. Lee [11]의 추진축계 진동론에 나와 있는 2행정 단동 과급 9 실린더인 선박 주기관의 추진축계에 대하여 적용하였다. 주기관의 요목은 Table 1과 같고, 축의 요목은 Table 2와 같고, 프로펠러의 요목은 Table 3과 같다.
Specifications of applied main engine
Specifications of shafting system
Specifications of propeller
3.2 축계의 고유진동수와 고유진동모드
축계의 관성모멘트와 강성은 앞에서 인용한 문헌의 자료를 그대로 써서 식 (7)의 고유치해석 하면 고유진동수와 고유진동모드를 구할 수 있다.
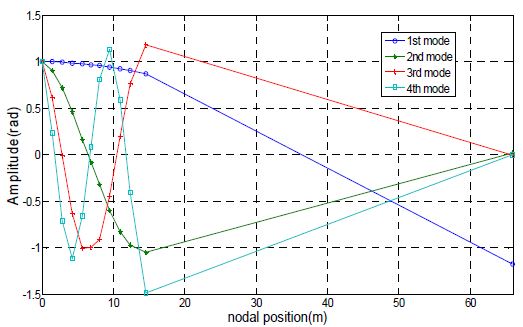
Figure 2에 고유진동모드를 보인다.
Natural vibration modes of the shaft system
Table 4는 위 문헌에서 실측한 고유진동수와 문헌에서 Holzer 법으로 구한 고유진동수와 식 (7)에 의한 고유치해석법을 이용하여 구한 고유진동수를 비교한 것이다.
Comparison of N.F. in various cases unit: Hz
표에서 알 수 있듯이 1차와 2차의 고유진동수는 모두 실측값과 잘 맞음을 알 수 있다. 또 고유치해석법을 이용하면 고차까지 고유진동수를 구할 수 있으나 Holzer법으로는 3차 이상은 구하기 어려움을 알 수 있다.
Table 5은 Holzer법을 이용한 경우와 고유치해석법을 이용한 경우의 관성토크 합을 보인다.
Summation of inertia torque
Table 5에서 알 수 있듯이 Holzer법을 사용하면 관성토크의 합이 1차에서 78,100, 2차에서 308,000 정도로 0에 수렴하지 않은 정도가 아닐 뿐만 아니라 상당히 큰 값임을 알 수 있는데, 같은 문제를 고유치문제로 풀면 최고차인 11차에서도 관성토크의 합이 –0.0279로 거의 0에 수렴한다.
3.3 축계의 강제진동 해석
3.2에서는 자유진동해석을 하여서 고유치해석법의 정확성을 보였다. 실험과 해석이 거의 일치한다는 사실은 질량관성모멘트와 강성의 계산이 제대로 이루어졌다는 것을 의미한다. 따라서 외력만 제대로 추정하면 강제진동도 정확히 예측할 수 있을 것으로 기대할 수 있다.
외력은 폭발에 의한 성분과 운동부의 관성에 의한 성분으로 나눌 수 있다.
| (14) |
여기에서 {Texp}는 폭발력에 의한 토크이고, {Tmoi}는 왕복관성력에 의한 성분이다. 폭발력에 의한 토크는 제작사가 제공하는 하모닉스 곡선에서 구하고, 왕복관성력에 의한 토크는 다음 식을 이용하기로 한다.
| (15) |
여기에서 Mrec는 피스톤, 크로스 헤드, 가이드 슈, 피스톤 냉각기, 연접봉의 왕복질량 등 전체 왕복질량을 나타내고, r은 크랭크샤프트의 회전반경이고, ω는 회전각속도를 나타낸다.
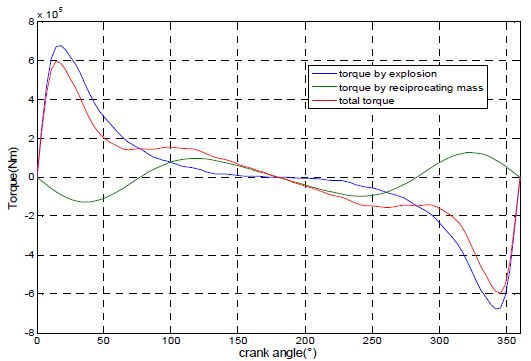
Figure 3에 토크 곡선을 보인다. 파란색이 폭발에 의한 토크이고, 녹색이 왕복질량에 의한 토크이고, 빨간 색이 이들의 합인 전체 토크를 나타낸다.
Torque curves
여기에서 외력인 토크 {T}는 엔진의 폭발순서가 1-6-7-3-5-8-2-4-9이므로 다음과 같이 쓸 수 있다.
여기에서 Tn은 n번째 하모닉스 성분을 나타내고, 모두 16개의 하모닉스 성분으로 나누고, 각 실린더에 적용하는 것이다. 이 시스템은 선형이므로 각각의 실린더에 대하여 따로 풀어서 전부 더하면 가해진 힘에 대한 응답을 구할 수 있다.
| (16) |
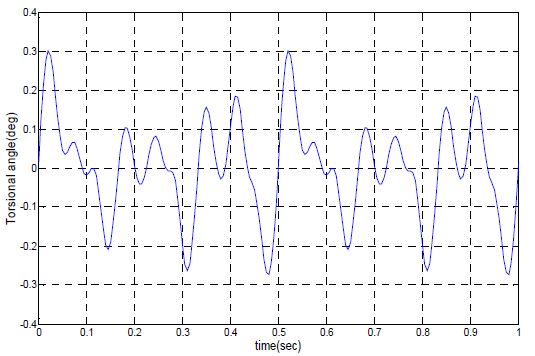
Figure 4는 200rpm으로 운전할 경우의 1번 크랭크샤프트의 응답을 보인다.
Forced vibration result of No.1 crank shaft at 120rpm
3.4 흡진기에 의한 진동 저감
여기에서는 흡진기에 의한 진동 저감 효과를 보인다.
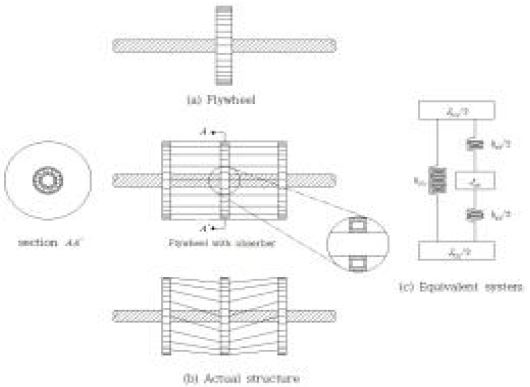
Figure 5에 제안한 동흡진기를 보인다. Figure 5 (a)는 통상의 플라이휠이고, Figure 5 (b)가 제안한 흡진기이다. 플라이휠을 둘로 나누어 설치하고, 중간에 자유롭게 회전할 수 있는 휠을 삽입하고 이를 양쪽으로 나뉜 플라이휠에 강선으로 고정시킨 형태이다. 외력이 작용하면 관성에 의하여 이 삽입된 휠은 원래의 위치를 고집하기 때문에 플라이휠과 위치가 틀어지게 되지만 강선의 장력에 의하여 원래의 위치로 돌아가게 되는 부진동장치가 되는 것이다. 이 부진동장치가 축진동 방향과 반대로 움직이면 제진장치가 되는 것이다. 이 부진동장치 즉 흡진기의 고유진동수는 휠의 질량관성모멘트와 강선의 강성에 의하여 결정된다. 강선의 강성은 강선에 걸리는 장력, 강선의 길이, 휠의 반지름에 의하여 결정되는데 소각도 진동한다면 다음과 같다.
Suggested flywheel dynamic absorber
| (17) |
여기에서 T는 강선에 걸리는 장력, L은 양쪽 플라이휠 사이의 거리, r은 휠의 반지름, n은 강선의 개수이다. 따라서 흡진기의 고유진동수는 다음과 같이 된다.
| (18) |
여기에서 ωabsb는 흡진기의 고유진동수, kabsb는 흡진기의 회전강성, Jabsb는 흡진기의 질량관성모멘트이다.
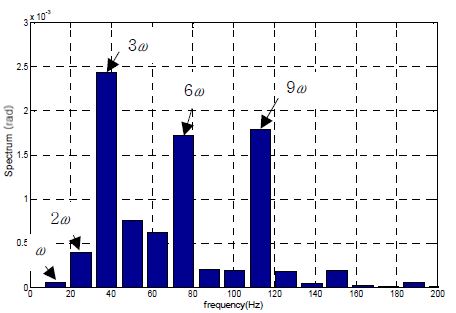
흡진기는 모든 진동을 잡아줄 수는 없고, 특정한 주파수의 진동을 잡아주는 것이다. 여기에서는 MCR에서 운전 중일 때의 진동을 줄이는 것을 목표로 한다. 9번 크랭크샤프트의 진동이 가장 컸으므로 9번을 해석 대상으로 한다. Figure 6는 9번 크랭크샤프트의 진동에 대한 스펙트럼을 보인다. MCR의 3배, 6배, 9배 성분이 매우 도드라지게 큼을 알 수 있다. 이 세 성분을 다 잡으려면 세 종류의 흡진기를 설치하여야 하지만 이것은 구조를 매우 복잡하게 하므로 여기에서는 이 중에서 하나만 선택하기로 하였다. 시도하여 본 결과 6ω의 고유진동수를 가지는 흡진기를 설치하는 것이 효과가 가장 좋았다.
Spectrum of response of No.9 crankshaft
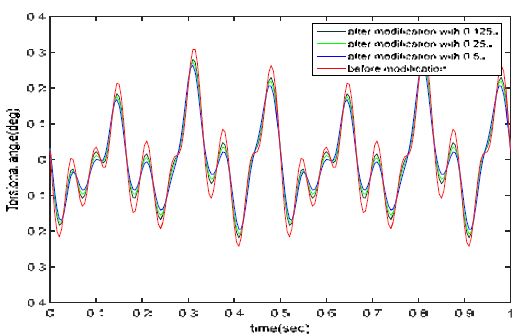
Figure 7이 9번 실린더에 흡진기를 장착한 경우의 진동 감소 효과를 보인다. 붉은색이 흡진기를 설치하기 전이고, 파란색이 플라이휠의 1/8에 해당하는 질량관성모멘트를 장착한 것이고, 녹색이 1/4, 검은색이 1/2의 질량관성모멘트를 가지는 흡진기를 설치한 경우에 대한 시뮬레이션 결과이다. 당연한 결과이지만 더 큰 질량관성모멘트의 감쇠기를 장착하면 다 좋은 결과를 보임을 알 수 있다.
The damping effects of suggested absorber at No. 9 crank shaft
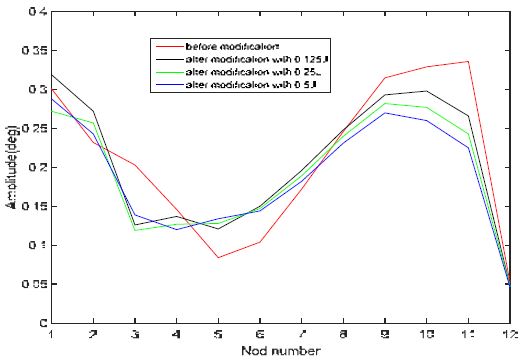
Figure 8은 각 절점에서의 진동 최대값을 보인다. 붉은색이 흡진기를 장착하기 전이고, 검은색이 플라이휠의 질량관성모멘트의 1/8에 해당하는 흡진기를 설치한 경우이고, 주황색이 1/4, 파란색이 1/2 짜리의 질량관성모멘트를 가지는 흡진기를 설치한 경우이다. 진동이 가장 큰 9번 크랭크샤프트에서의 진동이 1/8짜리는 10%, 1/4짜리는 16%, 1/2짜리는 21% 가량 줄어듦을 알 수 있다.
Vibration reduction effects of absorbers with various moment of inertia at each node.
4. 결 론
본 논문에서는 6기통 엔진의 진동해석과 동흡진기의 제안에 대하여 연구하여 다음과 같은 결론을 얻었다.
- 1. 엔진의 고유진동수를 Holzer법 대신 고유치해석법을 이용하여 고차까지 정확한 고유진동수를 구하여서 Holzer법으로는 저차의 2, 3 차 고유진동수까지 밖에 구할 수 없는 단점을 보완하였다.
- 2. 엔진 제작자가 제공한 하모닉스 표를 이용하여 강제진동 해석하는 법을 제시하고 그림으로 나타내었다.
- 3. 플라이휠을 변형하여 플라이휠 본연의 역할과 감쇠기의 역할을 할 수 있게 제안하여 좋은 감쇠 효과가 있음을 보였다.
제안한 감쇠기는 모든 운전 영역에서 효과를 발휘하는 것은 아니고 정속 운전을 하는 회전기기에 효과가 크다는 점을 밝혀둔다.
Acknowledgments
이 논문은 2015년 한국해양대학교 대학원 기관시스템공학과 박경일의 석사학위논문에서 발췌한 것입니다.
References
- Germanischer Lloyd, “Rules for Classification and Construction I Ship Technology”, (2013).
- ABS, “Guidance Notes on Ship Vibration”, (2006, April).
- J. S. Carlton, and D. Vlasic, “Ship vibration and noise: Some topical aspects”, 1st International Ship Noise and Vibration Conference, London, p1-11, (2005).
- IMO, “Adoption of The Code on Noise Levels on Board ships, Annex 1, Resolution MSC.337(91)”, (2012, November).
-
J. H. Moon, and J. R. Kim, “Study of two stroke low speed diesel engine crankshaft crack phenomenon by torsional vibration calculation & measurement”, Transactions of the Korean Society for Noise and Vibration Engineering, vol. 24, p452-461, (2014).
[https://doi.org/10.5050/KSNVE.2014.24.6.452]
-
S. Y. Park, K. H. Han, J. M. Park, S. H. Kwon, and O. S. Oh, “Optimum design of viscous fluid damper for reducing the torsional vibration of propulsion shaft system”, Transactions of the Korean Society for Noise and Vibration Engineering, vol. 25, p666-613, (2015).
[https://doi.org/10.5050/KSNVE.2015.25.9.606]
-
D. C. Lee, Q. D. Vuong, and T. K. Nam, “Torsional vibration phenomenon due to pulse torque of variable speed induction motor on rotating systems”, Transactions of the Korean Society for Noise and Vibration Engineering, vol. 25, p666-613, (2015).
[https://doi.org/10.5050/KSNVE.2015.25.6.414]
-
R. D. Barro, K. T. Eom, and D. C. Lee, “Transient torsional vibration response due to ice impact torque excitation on marine diesel engine propulsion shafting”, Transaction of Korean Society for Noise and Vibration Engineering, vol. 25, p321-328, (2015).
[https://doi.org/10.5050/KSNVE.2015.25.5.321]
- S. S. Lao, Translated by N. G. Park, Mechanical Vibration 4th Ed, NJ, USA, Pearson, p578-580, (2005).
- K. I. Park, Studies on the Analysis of Forced Torsional Vibration and the Design of Dynamic Absorber, M.S. Thesis, Department of Marine System Engineering, Korea Maritime and Ocean University, Korea, (2015).
- H. J. Jeon, and D. C. Lee, Vibration of Propulsion Shafting, Busan, Korea, Dasom publishment, p173-220, (2003).