상용 소프트웨어를 이용한 스파크 점화 기관의 시뮬레이션에 관한 연구
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
연료 경제와 유해 배출 가스 저감을 목적으로 최근 들어 LNG 또는 합성 가스를 사용하는 박용 가스 기관이 주목받고 있다. 예혼합 연소를 하는 오토 사이클로 작동하는 가스 기관을 구현할 경우 EGR 또는 SCR을 적용하지 않고도 Tier III의 규제를 충족할 수 있는 것으로 확인되고 있다. 본 연구에서는 오토 사이클로 작동하는 기관에 대한 시뮬레이션 기술을 산업 기술 현장에 제공하기 위한 목적으로, 실험적으로 접근이 용이한 소형 가솔린 기관을 대상으로 상용 소프트웨어인 BOOST를 이용한 시뮬레이션을 시행하였다. 이 연구는 두 단계로 구성되어 이미 시행한 첫 번째 단계에서는 흡기 및 배기 계통에 대한 최적의 모델링 방법에 관한 연구가 수행되었다. 이번 연구는 이전의 연구에서 선정된 흡·배기 계통의 해석 모델을 적용한 상황에서 실린더 내 과정을 해석하고 최종적으로 주요 성능 인자들을 계산하는 방법을 정립하였다. 이 연구를 통하여 실험에의 의존이 적은 연소 및 열전달 모델과 밸브 유량계수 모델을 선정하고 관련 상수들을 결정하는 방법을 확립하였다. 이들을 이용하여 실린더로 유입되는 공기량, 실린더 내 순간 압력 변화 및 도시평균유효압력을 효과적으로 예측할 수 있음을 확인하였다.
Abstract
In recent years, gas engines fueled with LNG or synthetic gas have been attracting considerable attention for marine use owing to their potential to facilitate better fuel economy and to reduce emissions. It has been confirmed that gas engines using the Otto cycle, which involves premixed combustion, can satisfy Tier III regulations without the EGR or SCR system. The objective of this study is to acquire simulation technologies for predicting gas engine performances in industrial fields. Using the commercial software BOOST, the simulation is conducted on a gasoline engine rather than a marine engine due to the gasoline engine’s easier accessibility. This study consists of two stages. In the first stage published previously, the optimal modeling techniques for representing the behavior of the gas in the intake and exhaust systems were determined. In the current study, we formulated a method to evaluate the combustion and heat transfer processes in the cylinder and to ultimately determine the major performance parameters, given that the analytical model derived from the previous stage has been applied. Through this study, we were able to determine a combustion and heat transfer model and a valve discharge coefficient that are less reliant on empirical data: we were also able to formulate a methodology through which relevant constants are decided. We confirmed that the values of transient cylinder pressure variation, indicated mean effective pressure, and air supply can be successfully predicted using our modeling techniques.
Keywords:
Gas engine, Otto cycle, BOOST, Simulation, Performance prediction키워드:
가스기관, 오토 사이클, 부스트, 시뮬레이션, 성능예측1. 서 론
선박의 추진과 보기 구동에 있어서 연료 경제와 유해 배출 가스 저감을 목적으로 최근 들어 LNG 또는 합성 가스를 사용하는 가스 기관이 주목되고 있다. 주⦁보기용 4행정 사이클 기관에 이어 최근에는 주기관용 2행정 사이클 기관에도 가스 연료가 적용되어 출시된 바 있다. 박용 가스 기관은 기본적으로 기존의 디젤 기관을 원형으로 하므로 가스를 연료로 하는 경우에도 우선적으로 디젤 사이클로 작동하도록 설계되었다. 그러나 예혼합 연소를 전제로 하는 오토 사이클로 작동하는 가스 기관을 구현할 경우 EGR 또는 SCR을 적용하지 않고도 Tier III의 규제를 충족할 수 있는 것으로 확인되고 있다[1]-[3].
오토 사이클로 작동하는 가스 기관에 관한 연구 개발에 있어서는 박용 기관의 특성 상 시뮬레이션을 통한 성능 해석이 필수적이다. 그러나 주로 디젤 기관을 다루었던 박용 기관 제작사의 입장에서는 오토 사이클 기관에 대한 해석 경험이 적은 편이다. 현재의 주요 박용 기관은 일부를 제외하고는 대부분 해외 설계 회사와의 기술 제휴에 의해 이루어진다. 우리 제작사의 입장에서는 개발 설계 또는 성능 개선을 위한 설계 변경 단계에서 자체적인 사이클 해석을 통해 우리의 의견을 적극 반영하여야 하나, 오토 사이클에 대한 해석 경험이 일천한 관계로 자체의 해석 결과를 신뢰 받지 못하고, 신뢰성이 검증된 상용 소프트웨어를 이용하도록 요구 받고 있으며, 이와 함께 소프트웨어 운용에 있어서도 외국 용역 회사에 의한 성능 해석 결과를 제출할 것을 요구 받고 있는 실정이다. 이에 제작 현장에는 계속적으로 상용 소프트웨어를 이용한 시뮬레이션 기술에 대한 경험을 축적하여 우리의 역량을 인정받을 필요를 절감하고 있다. 특히 해석 경험이 일천한 오토 사이클의 성능 해석에 대한 경험 축적이 시급하게 요구된다.
본 연구에서는 기술 현장에서 오토 사이클로 작동하는 기관에 대한 시뮬레이션 기술을 확보하고 경험을 축적하기 위한 목적으로 시행되었다. 최종적인 목표는 가스를 연료로 하는 박용 기관이지만 이 기관에 대한 직접적인 실험이 곤란하므로 열역학적으로 동일한 원리로 작동하고 비교적 접근이 용이한 소형 가솔린 기관을 대상으로 하여 시뮬레이션 기술, 특히 성능 해석 방법을 확보하고 이의 검증을 위해 해석 결과를 실험값과 비교하였다.
기관에 대한 성능 해석은 실린더 내의 과정에 대한 해석과 함께 흡⦁배기 계통에서의 해석으로 이루어진다. 이 두 가지 계통의 해석은 서로 영향을 미칠 수 있으므로 저자들은 이전의 연구[4]에서 실린더 내 압력 변화를 실험값으로 부여한 상태에서 최적의 흡⦁배기 계통 모델을 설정하는 연구를 수행하였다. 본 연구에서는 이전의 연구를 토대로 흡⦁배기 계통의 해석 모델을 선정, 적용한 상황에서 실린더 내 과정을 해석하는 방법에 대한 연구를 수행하였다. 실린더 내 과정을 해석하기 위해서는 연소과정과 열전달 과정에 대한 모델을 설정하여야 한다. 아울러 실린더 내로 유입한 동작유체의 양을 정확히 산정하기 위해 흡⦁배기 계통에 대한 적절한 모델링과 함께 흡⦁배기 밸브 유량계수의 값이 적절히 적용되어야 한다.
연소 과정의 해석을 위해서는 여러 가지 방법들이 제안되고 있지만, 효과적인 시뮬레이션을 위해서는 대상 기관과 해석 목적에 따라 적합한 모델의 설정과 함께 그에 포함되는 실험 또는 보정 상수들을 적절히 선정하여야 한다. 특히 모델에 포함된 상수를 대상 기관에 맞게 선정하는 것은 성능 해석에 있어서 매우 중요한 기술 중의 하나이다. 본 연구에서는 대상 기관의 성능을 해석하기 위해 박용 기관 제작사에서 널리 사용하고 있는 상용 소프트웨어 중의 하나인 AVL BOOST를 사용하였다. 본 연구에서는 최소한의 제한된 자료를 가지고 연소를 포함한 실린더 내 과정을 해석하는 방법을 시도하였다. 일반적으로 기관의 개발 과정에서는 목표로 하는 평균유효압력과 함께 유사한 기존 기관으로부터 도출할 수 있는 실린더 최고 압력의 예상값을 가지고 있다. 그러므로 기준 운전조건에서의 평균유효압력과 실린더 최고 압력을 가지고 연소 모델과 열전달 모델에서 요구되는 상수를 결정하는 방법을 사용하여 연소 모델과 열전달 모델에 포함되는 상수들을 별도의 실험 없이 결정함으로써 기술 현장에서 용이하게 사용할 수 있는 시뮬레이션 기법을 제공하고자 하였다.
2. 이론해석
실린더 내에서 크랭크 각에 따라 변화하는 가스의 상태량을 계산하기 위해 열역학 제1법칙 등을 적용하여 정리하면 크랭크 각에 따른 실린더 내 가스의 온도 변화를 나타내는 다음 식을 구할 수 있다[5][6].
| (1) |
위의 식에 의해 크랭크 각에 따른 온도 변화율이 계산되면 적절한 적분 기법에 의해 매 시간(크랭크 각) 단계에서의 실린더 내 가스의 온도가 결정되고 이상기체 상태식에 의해 동일한 시간 단계에서의 압력이 결정된다.
식 (1)의 우변 두 번째 항은 연료의 연소에 의한 열발생율을 나타내며, 세 번째 항은 벽면 및 피스톤으로의 열손실을 나타낸다. 네 번째와 다섯 번째 항은 실린더로 또는 실린더로부터의 질량의 유출입에 따른 에너지 유출입을 나타내고 있다. 실린더 내에서의 상태 변화를 정확히 계산하기 위해서는 이들 항을 적절히 모델링하는 것이 중요하다.
저자들의 이전 연구[4]에서 흡·배기 계통에서의 시뮬레이션에 관련한 이론적 내용을 이미 설명하였기 때문에 본 논문에서는 실린더 내의 열역학적 과정에 대한 시뮬레이션에 대해 설명하며 그 중에서도 특히 연소과정에 대한 모델링과 열전달과정에 대한 모델링 및 밸브 유량계수의 산정에 대하여 설명한다.
2.1 열발생율의 계산
식 (1)의 두 번째 항인 열발생율을 계산하기 위해서는 실린더 내에서의 연소 과정을 적절히 모델링하여야 한다. BOOST에서 오토 사이클을 해석하기 위하여 제공하는 연소과정 모델링은 Wiebe Model, Wiebe Two Zone Model, Hire et al Model, Fractal Combustion Model 등이 있으며, 이 모델들에 대해서 간단히 살펴보면 다음과 같다.
열발생율을 가장 편리하게 나타내는 방법으로 사용되는 Wiebe 함수는 연소 질량분(Burnt Mass Fraction)을 다음과 같은 식으로 나타내고 있다[7][8].
| (2) |
여기서 y는 총 연소지속기간 중에서 이미 연소가 일어난 기간이 차지하고 있는 비율을 표시한다. Wiebe 함수가 가지는 변수는 Wiebe 계수 a와 형상인자 m, 연소지속기간 ∆αc 및 연소시작점 등이다. 연소의 완결성(Completeness of Combustion)을 나타내는 Wiebe 계수 a는 완전연소의 경우 6.9의 값을 가진다[7][8]. 이외 3개의 상수들은 기관부하나 기관회전속도에 따라 상수 값들을 다르게 정해 주게 된다. 이 값들의 적절성 여부가 성능 예측에 있어서 주요한 문제가 된다.
Wiebe Two Zone Model은 Wiebe 연소함수를 기본으로 하며 실린더 내를 기연영역(Burnt Zone)과 미연영역(Unburnt Zone)의 두 영역으로 나누어 생각한다. 각각의 영역에서 압력은 동일하지만 온도는 영역별로 다른 것으로 간주한다. 이 모델을 사용할 경우 이론적으로는 보다 정교한 계산이 가능하고 노크의 발생을 고려할 수 있다는 이점이 있으나 상수가 많아지고 이들 값의 결정이 어려운 단점이 있으므로 학술적인 연구가 아닌 경우는 활용성이 떨어진다[7].
기관 내에서의 열발생 특성은 운전조건마다 달라진다. 그러므로 흡기관 압력과 기관 회전속도 등의 운전조건이 달라짐에 따라 서로 다른 열발생율 곡선을 입력하여야 한다. Hire 등은 연소지속기간과 점화 지연 기간을 운전조건에 따라 산정하는 식들을 다음과 같이 제시하였다[7][9].
| (3) |
| (4) |
기준으로 삼은 운전 조건에 대해 BOOST에서 연소지속기간, 연소 개시 시점에서의 피스톤과 실린더 헤드 사이의 거리 및 층류화염속도 등을 계산하면 위의 관계식들에 의해 주어진 운전조건에서의 연소지속기간과 점화지연을 계산할 수 있다.
이 모델은 예혼합연소에서 열발생율을 예측하도록 고안된 모델로 열발생율을 예측하기 위해 연소실 형상, Spark Plug의 위치, 실린더 내 가스의 화학적 조성 및 실린더 내에서의 가스의 유동과 난류 등을 고려한다[7]. 이 모델을 사용하기 위해서는 자세한 연소실 형상을 입력해 주어야한다. 아울러 점화지연에 관련한 두 개의 상수, 난류강도를 결정하기 위한 세 개의 상수와 벽면 연소(Wall Combustion)에 관련한 한 개의 상수를 결정해 주어야 한다. 이 상수들 중 세 개는 추천값으로 정해질 수 있으나 나머지 상수들을 결정하기 위해 상당히 복잡한 과정과 자료를 요구하게 되므로 현장에서 최소한의 자료를 가지고 주요 성능 인자를 예측하고자 하는 본 연구의 목적과는 부합하지 않는다.
2.2 열손실의 계산
식 (1)의 세 번째 항에 나타난 연소실 벽면 및 피스톤 상면으로의 열전달은 다음 식으로 계산한다[10][11].
| (5) |
손실되는 열에너지는 실린더 헤드와 실린더 벽면(또는 라이너가 있는 경우 라이너 벽면) 및 피스톤 크라운으로의 열전달을 각각 따로 계산해야 하며 이를 위해 열전달 계수 를 결정해 주어야 한다.
열전달과정을 해석하기 위하여 BOOST에서 제공되는 열전달 모델들에 대해서 간단히 살펴보면 다음과 같다.
열전달 계수는 압축, 팽창의 고압 사이클 부분과 흡기 및 배기의 가스 교환 과정에 대해서 각각 다른 열전달 계수를 적용한다. 고압 사이클에서의 열전달 계수는 다음과 같이 나타낸다[7][10].
| (6) |
여기서
| (7) |
C2는 직접 분사 기관의 경우 0.00324의 값을 갖는다. 가스 교환 과정에 대한 열전달 계수는 다음 식과 같이 계산된다.
| (8) |
여기서 C3은 다음 식으로 표시된다.
| (9) |
이 모델은 부분 부하 조건에서 열전달을 보다 정확하게 계산하기 위해 Woschni 1978 모델을 수정한 모델로서 고압 사이클의 계산에서 도시평균유효압력(IMEP:Indicated Mean Effective Pressure)의 값이 설정값 이하로 작아지게 되면 열전달 계수의 값을 다음과 같이 수정하도록 한 것이다[7].
| (10) |
이 때 다음의 조건에서는 열전달 계수로서 식 (6)을 사용한다.
| (11) |
가스 교환 과정에 대해서는 Woschni 1978 모델과 동일한 관계식을 사용한다.
Hohenberg 모델은 Woschni 모델과 유사하나 보다 단순화된 형태를 가지고 있다[7].
| (12) |
AVL 2000 모델은 Woschni식을 가스교환과정에 대해 수정한 식으로 가스교환과정 중의 열전달 해석을 보다 정확하게 나타내고 있다. 이 모델에서는 포트 길이에 따라 포트의 직경이 변화하는 양상을 자세히 입력하여야 한다.
2.3 밸브를 통한 에너지 유출입의 계산
실린더로 출입하는 동작유체의 유량을 정확히 산정하기 위해서는 흡·배기 계통에서의 상태량을 정확히 계산하는 것과 함께 흡기 및 배기밸브에서의 밸브유량계수의 값을 적절하게 산정하여야 한다.
흡·배기 계통에서의 상태량을 계산하기 위해 흡·배기 계통에서의 위치와 시간에 따른 상태량의 변화를 Wave Action 모델을 사용하여 계산하였으며 이는 저자들의 이전의 연구[4]에서 설명한 바 있다.
3. 기관의 모델링과 실험
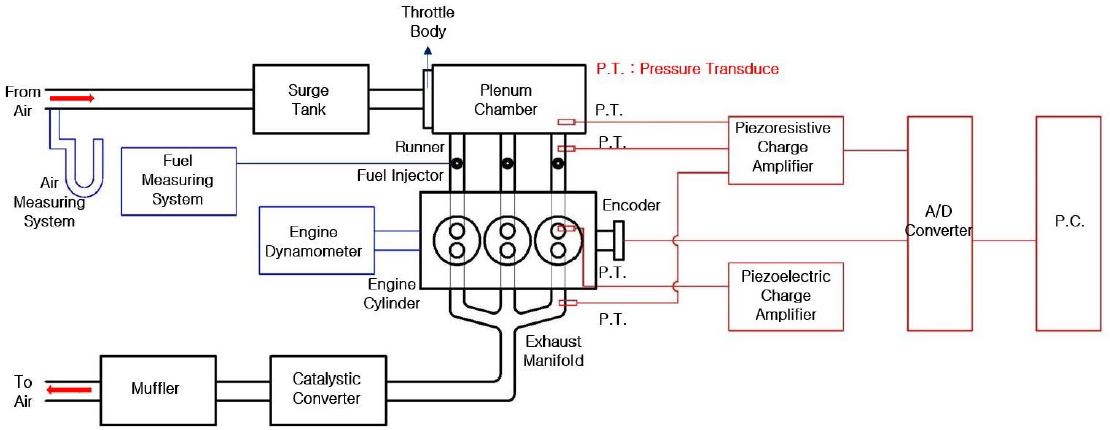
해석의 대상으로 삼은 기관은 3개의 실린더를 가진 수냉식 MPI 가솔린 기관으로서 흡기 계통은 서지탱크와 스로틀 바디, 플레넘 체임버, 연료 인젝터 및 흡기 러너로 구성되어 있으며 배기 계통은 배기 매니폴드와 촉매 변환기 및 소음기로 이루어져 있다. Figure 1은 본 연구에서 해석의 대상인 기관과 실험 장치를 나타내고 있다.
Schematic Diagram of Test Engine
3.1 흡·배기 계통의 모델링
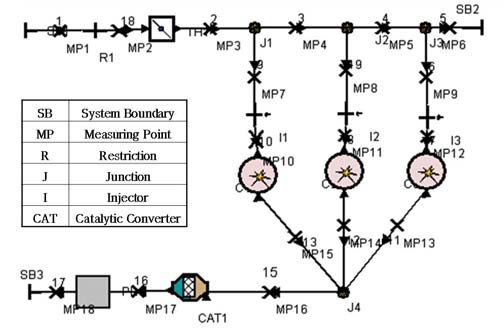
본 연구에서 대상으로 삼은 기관은 플레넘 체임버가 스로틀 바디 하류에 위치하고 있으며 여기서 신기는 러너를 통하여 3개의 실린더 각각으로 유동하도록 되어 있다. 이중 플레넘 체임버를 모델링하는 방법으로는 플레넘 체임버를 한 개의 경계점으로서 일정한 체적을 가진 하나의 탱크로서 모델링하는 방법과 플레넘 체임버를 여러 점에서 러너와 연결된 관으로서 모델링하는 두 가지 방법이 있다. 선행된 연구[4]에서는 두 경우의 계산의 정확도가 거의 비슷한 결과를 나타내었다. 본 연구에서는 흡기계통에서의 압력파의 거동을 보다 자세히 관찰하기 위해 플레넘 체임버를 관으로 간주하여 모델링하였다. 배기 매니폴드 및 소음기를 해석하기 위해 여러 모델을 시험하였으며 이 결과 배기 매니폴드는 3개의 관이 한 지점에서 하나의 관으로 합쳐지는 것으로 모델링하였다. 소음기의 경우도 이전의 연구 결과에 따라 커다란 체적을 가지는 하나의 관으로 모델링하였다. 이상과 같이 모델링한 형상을 Figure 2에 나타내었다.
Modeling Configure of Test Engine
3.2 밸브 유량계수의 결정
실린더 내의 상태량과 함께 밸브 전후에서의 상태량이 정확히 계산되었다 하더라도 실린더를 출입하는 질량 유량을 정확하게 계산하기 위해서는 밸브 유량 계수를 정확하게 산정하여야 한다. 밸브 유량계수는 해당 기관의 밸브를 대상으로 별도의 실험 장치를 구성하고 실험에 의하여 도출하는 것이 가장 바람직하며 이에 관한 여러 연구 결과들이 제시된 바 있다[12]. 그러나 기술 현장에서는 이 자료를 확보할 수 없는 경우가 많다. Benson et al. [13]은 밸브 유량계수에 관한 자료가 없을 경우 실험에서 나타난 실린더 공급 공기량이 계산값과 일치할 때까지 밸브 유량계수를 시행착오에 의해 찾아내는 방법을 시도하기도 하였다. 이 방법은 밸브 유량계수에 대한 실험 자료가 없을 경우 편리하게 적용할 수는 있으나 공급 공기량에 관한 실험 자료에 의존하여야 하고 또한 사이클 전체에 걸쳐 일정한 유량계수 값을 적용하여야 하는 단점이 있다. Noyes [14]는 Poppet Valve에 대해 기존에 나와 있는 유량 계수의 자료들을 분석, 종합하여 밸브의 유량계수를 밸브 양정과 유동 방향 및 밸브 전후 압력비 등의 함수로서 나타내었다. Noyes의 식은 다음과 같이 표시된다.
| (13) |
여기서 상수 a, b, c, e, r 및 f는 밸브의 종류(흡기 및 배기), 유동방향(유입 및 유출)과 밸브 전후의 압력비 그리고 Seat Angle에 따라 다른 값을 갖는다. 각 경우에 따른 상수들의 값은 참고문헌에 수록되어 있다. 본 연구에서는 밸브 유량계수를 산정하는데 있어서 별도의 실험을 통하지 않고 Noyes의 식을 사용함으로써 실험 자료에의 의존을 최소화하고자 하였다.
Noyes의 식은 실제 유동이 일어나는 밸브 포트의 측면적을 기준으로 하고 있다. 반면 BOOST에서 적용되는 유량계수는 포트 면적을 기준으로 하고 있으므로 다음과 같이 Noyes 식을 수정하여 적용하였다.
| (14) |
3.3 연소과정 모델링
본 연구에서는 BOOST에서 제공하는 여러 가지 연소과정 모델링 중 실험자료에 많이 의존하여야 하는 Fractal Combustion Model은 배제하고 Wiebe Model과 Hire et al Model을 조합하여 적용하였다.
Wiebe 함수를 이용한 모델은 다른 연소모델과 비교하면 비교적 간단하기 때문에 정밀하고 정확한 값을 예측하기 어려울 수 있다. 그러나 대상 기관에 대한 자료가 제한되어 있는 상태에서 시뮬레이션을 할 경우에는 상수가 적게 포함되어 있는 Wiebe 함수를 사용하는 것이 유리하다.
식 (2)에 나타난 바와 같이 Wiebe Model에 포함되는 상수는 Wiebe 계수인 a와 형상인자 m 및 연소지속기간 등이 포함된다. 이 값들은 대상 기관의 특성 및 운전조건에 따라 다른 값이 부여되어야 한다. BOOST에서는 완전연소의 경우 a의 값으로 6.9를 추천하고 있으며 m의 값은 운전조건의 변화에 따라 달리 정해주기도 한다[7]. BOOST에서는 SI 기관의 경우 m의 값으로서 2.5를 추천하고 있으며 본 연구에서는 이 값을 모든 운전조건에 대해 동일하게 적용하였다. 따라서 사용자가 정해주어야 하는 상수는 운전조건에 따라 달라지는 연소지속기간 하나로 압축할 수 있었다.
본 연구에서는 대상 기관에 대한 연소 및 열전달 관련 상수를 실험적으로 결정할 수 없는 상황에서 간접적으로 정해주는 방법을 시도하였다. 새로운 기관의 설계는 현존하는 유사한 기관을 원형으로 이에 대한 설계 변경에서부터 시작한다. 새로운 기관에 대해서는 역학적으로 한계가 되는 실린더 최고 압력이 설정되어 있으며 평균유효압력은 원형이 되는 기관과 거의 같거나 또는 새로운 목표값이 설정된다. 즉 대상이 되는 기관의 실린더 최고 압력과 평균유효압력은 설계값으로 주어지는 경향이 있으므로 이 값을 만족하도록 하는 연소 및 열전달 상수를 간접적으로 찾아내는 방법을 사용하였다. 이를 위해 먼저 연소지속기간과 열전달 관련 상수가 실린더 최고압력, 평균유효압력 및 공기공급량 등 주요 성능인자에 미치는 영향을 검토하였다.
Table 1은 연소지속기간의 변화에 따른 성능인자의 값을 비교하여 나타내고 있다. Table 1에서 보듯 연소지속기간이 증가할수록 실린더 최고압력은 감소하는 결과를 나타내고 있다. 연소지속기간의 변화가 도시평균유효압력과 공기량의 계산에 미치는 영향은 유효숫자 범위 내에서 거의 없음을 확인할 수 있다.
Effect of Combustion Duration on Performances. (2500 rpm, -100 mmHg)
3.4 열전달 모델링
본 연구에서는 BOOST에서 제공하는 여러 가지 열전달과정 모델링 중 Ryu의 연구[15]를 통해 가장 정확도가 높았던 Woschni 1990 Model을 적용하였다. 이 모델에 포함되어 있는 각종 상수들은 그대로 적용하되 최종적으로 계산된 열전달량 전체에 대한 보정은 따로 해 주어야 한다. 이 역할을 하는 것이 열전달 보정계수이며 보정계수로 인해 열전달 모델에 의해 계산되는 열전달 값을 증가하거나 감소하여 적용할 수 있다. Table 2는 열전달 보정계수가 실린더 최고 압력, 도시평균유효압력 및 공기량의 계산값에 미치는 영향을 나타낸 것이다.
Effect of Heat Transfer Calibration Factor on Performances. (2500 rpm, -100 mmHg)
Table 2에서 확인할 수 있듯이 열전달 보정계수는 실린더 최고 압력, 도시유효평균압력 및 공기 공급량의 계산 모두에 영향을 미치는 것으로 나타나고 있다.
정량적으로 살펴보면 열전달량이 4배가 증가할 경우 실린더 최고 압력은 12 % 정도 변화하고 있는데, 도시평균유효압력은 37 % 정도 변화하고 있다. 아울러 공기량의 계산에 미치는 영향은 아주 작은 것을 알 수 있다. 따라서 열전달 보정계수는 우선적으로 도시평균유효압력에 큰 영향을 미치며 부차적으로 실린더 최고압력에도 일부 영향을 미치고 있는 것으로 판단할 수 있다.
이상과 같은 경향을 볼 때 특정 운전조건에서 실린더 최고 압력과 도시평균유효압력의 실험값을 고려하여 연소지속기간과 열전달 보정계수를 정할 수 있다. 특정의 기준 운전조건에 대해 실린더 최고 압력과 도시평균유효압력을 고려하여 열전달 보정계수의 값을 정하고 이 값을 전 운전조건에 대해 동일하게 적용하였다. 이 조건에 대해 실험에서 나타난 (또는 목표 설정값에 해당하는) 실린더 최고 압력을 나타나게 하는 연소지속기간이 결정되면 다른 운전조건에서의 연소지속기간은 식 (3)에 의해 결정하도록 하였다. 따라서 연소 모델링에 필요한 자료가 절대적으로 모자라는 기술 현장에서 실험 상수에의 의존을 최소화하도록 하였다.
3.5 실험
시뮬레이션을 위하여 적용한 모델들과 상수의 적합성을 검증하기 위해 여러 운전조건에서 실린더 내와 흡·배기 계통 주요 지점에서의 순간 압력의 변화, 도시평균유효압력, 실린더로 유입한 동작유체의 양 등의 변화를 측정하고 이를 시뮬레이션을 통한 계산값과 비교하였다. 운전조건은 전부하 운전조건(W.O.T.)과 함께 부분 부하 운전조건인 흡기관 압력 –100 mmHg 및 –200 mmHg에서 기관회전속도를 1500 rpm에서 4000 rpm으로 변화시킨 경우에 대하여 검토하였다. 모든 운전조건에서 혼합비는 이론혼합비를 유지하였으며, 아울러 각 운전조건에서 MBT 점화시기를 유지하였다. 실린더 내의 순간 압력 변화는 압전형 압력변환기(Piezoelectric Pressure Transducer: Kistler 601A)를 실린더 헤드에 삽입하여 측정하였으며, 흡·배기 주요 계통에서의 순간 압력 변화는 절대 압력의 변화를 직접 측정할 수 있는 압저항형 압력변환기(Piezoresistive Pressure Transducer: Kistler 4075A10)들을 사용하여 측정하였다.
4. 결과 및 고찰
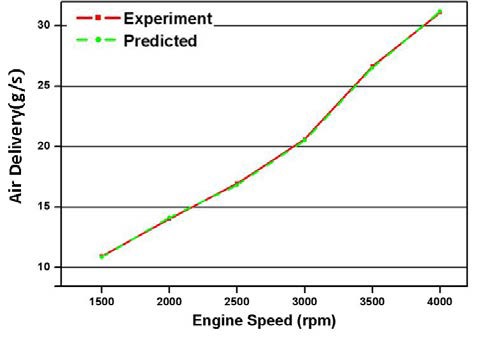
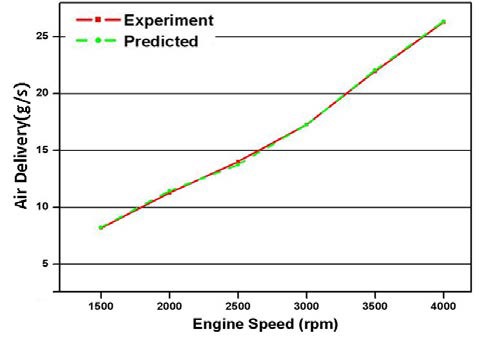
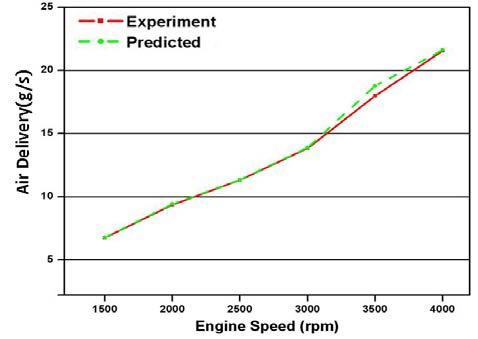
Figure 3 ~ Figure 5는 전부하 운전조건과 흡기관 압력을 각각 –100 mmHg 및 –200 mmHg로 유지한 상태에서 기관 회전속도를 1500 rpm에서 4000 rpm까지 운전시켰을 경우 실린더 내로 공급된 동작유체의 질량을 계산한 값을 실험값과 비교하여 나타낸 것이다. 대부분의 운전조건에 대하여 운전조건에 따른 동작유체의 질량의 변화 경향이 계산값에 잘 반영되고 있으며, -200 mmHg에서 3500 rpm인 운전조건을 제외하면 대부분 실험 결과에 정량적으로도 잘 일치하고 있다.
Air Delivery(W.O.T.)
Air Delivery(-100 mmHg)
Air Delivery(-200 mmHg)
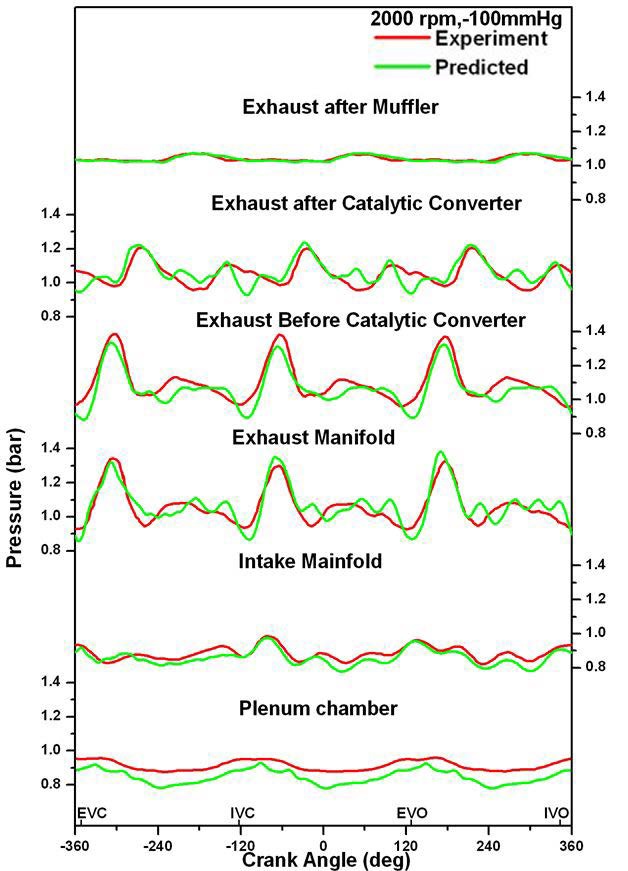
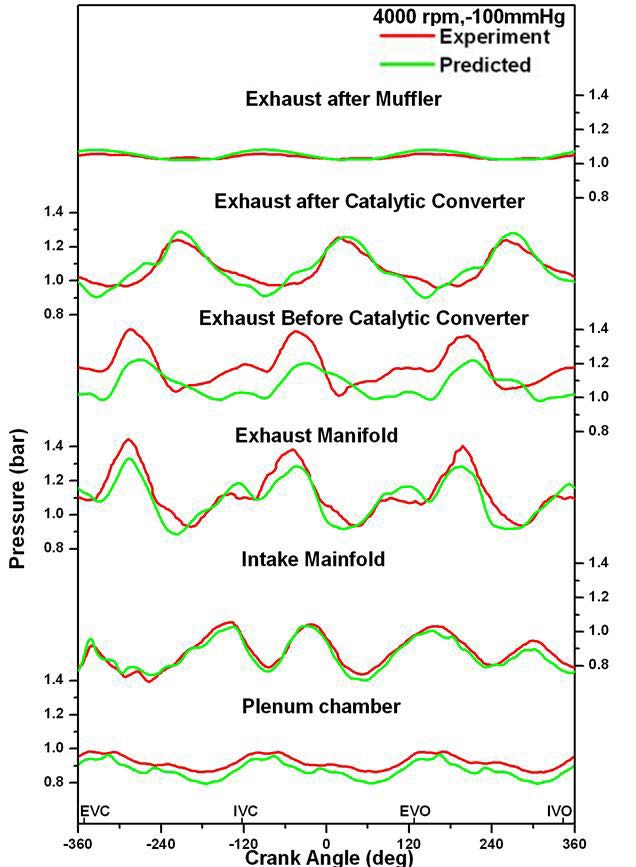
Figure 6과 Figure 7은 흡기관 압력 –100 mmHg인 부하 조건에 대해 기관회전속도 2000 rpm과 4000 rpm의 두 가지 경우에 대해 흡·배기 계통 주요 지점들에서의 순간 압력 변화를 보여주고 있다. 일부 지점에서 미세한 차이를 보이는 부분이 있으나 전반적으로 실험에서 나타난 압력파의 변화 경향이 계산에 비교적 잘 반영되고 있음을 나타내고 있다.
Pressure Variations at Various Locations in the Intake and Exhaust Systems(2000rpm,-100mmHg)
Pressure Variations at Various Locations in the Intake and Exhaust Systems(4000rpm,-100mmHg)
이상의 결과는 흡·배기 계통에 대한 여러 모델링 기법의 적용과 밸브 유량계수의 산정이 비교적 적절하게 이루어졌음을 뒷받침하는 것으로 판단된다. 특히 공기 공급량의 예측 결과를 볼 때 성능예측을 위한 시뮬레이션에 있어서 밸브 유량계수에 대한 실험 자료가 없을 경우 Noyes의 식이 훌륭한 대안이 될 수 있는 것으로 판단할 수 있다.
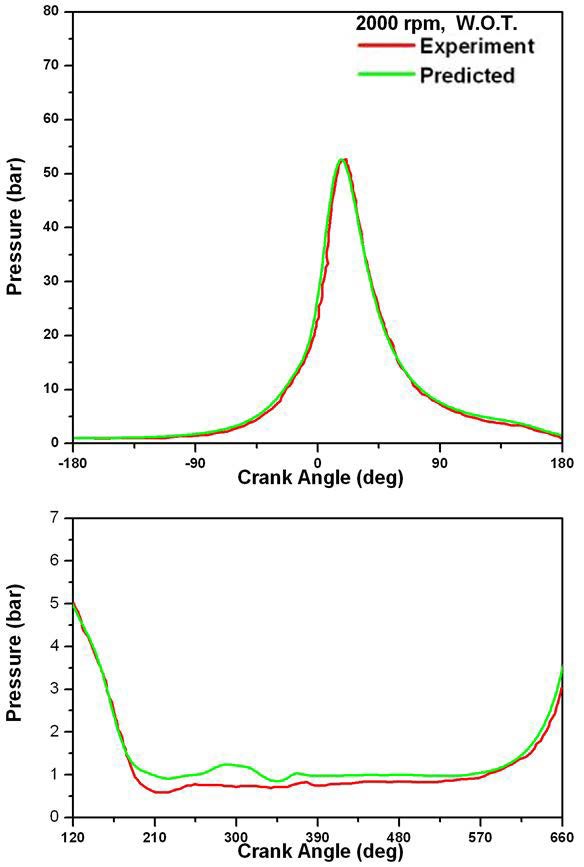
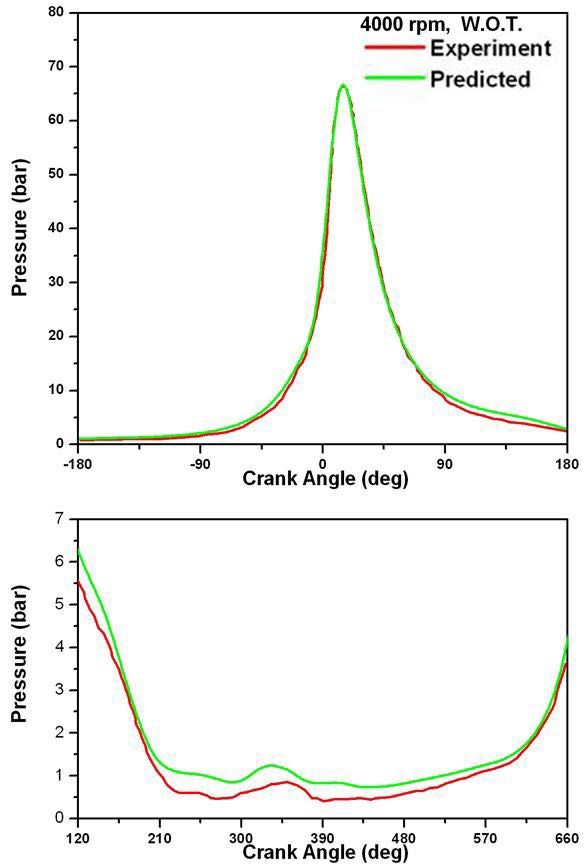
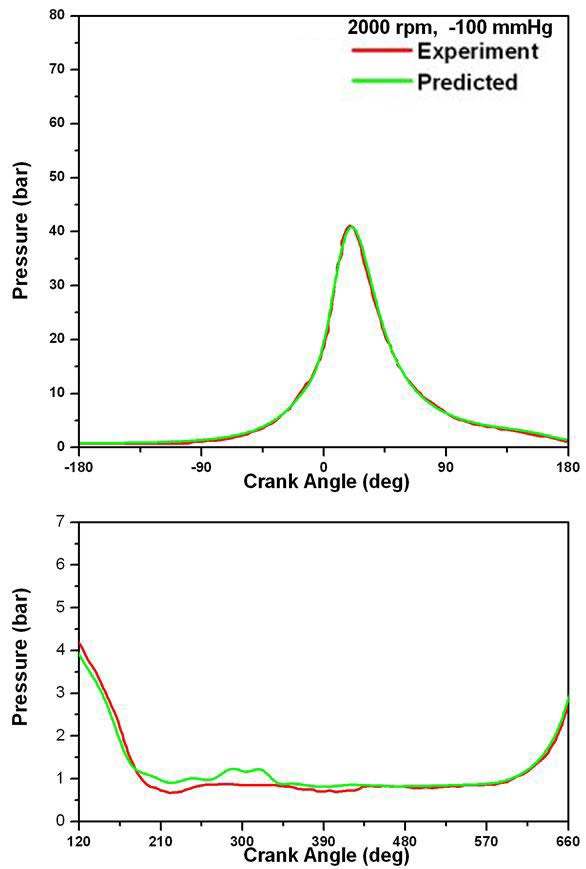
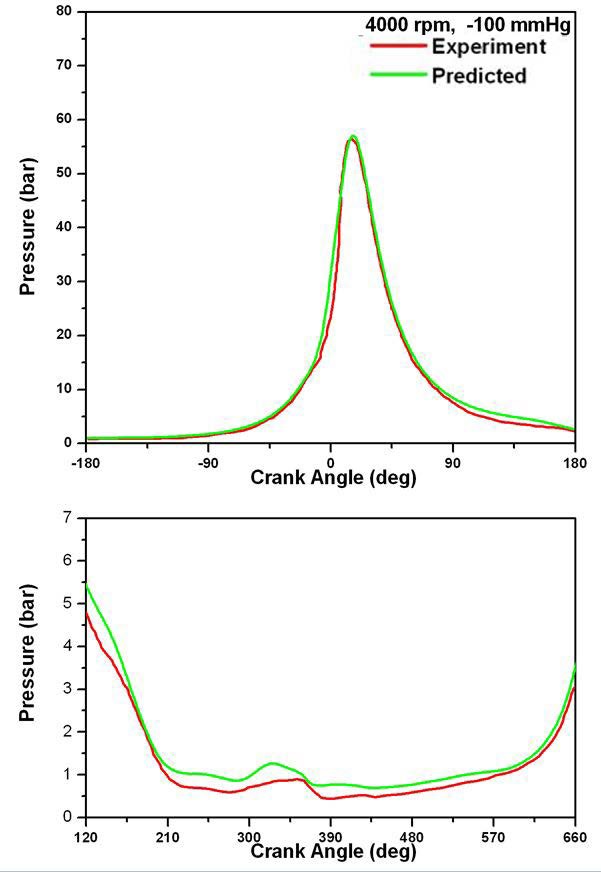
Figure 8 ∼ Figure 11은 몇 가지 운전조건에 대해 기관회전속도의 변화에 따른 실린더 내의 압력변화를 고압 사이클 부분과 흡·배기 과정 부분으로 나누어 도시한 것이다. 그림에 나타난 모든 조건에 대하여 실린더 최고 압력 및 최고 압력이 나타난 이후의 팽창과정은 잘 계산되고 있다. 하지만 압축과정 중의 압력 상승이 실험값에서 나타난 것 보다 약간 빠르게 이루어짐을 알 수 있다. 압축 과정에서는 연소의 영향이 없음을 감안할 때 이 과정에서의 오차는 열전달에 관련된 것으로 추정할 수 있다. 흡·배기 과정에서의 실린더 압력변화도 실험에서 나타난 경향을 잘 예측하고 있다. 흡·배기 과정 중의 압력변화의 예측값은 실험에서 보다 다소 높게 나타나고 있다. 그러나 이 부분에서의 압력 눈금이 크게 확대되어 있음을 고려할 때 정량적으로 우려할만한 오차는 아닌 것으로 생각된다.
The Variation of Cylinder Pressure (2000 rpm, W.O.T.)
The Variation of Cylinder Pressure (4000 rpm, W.O.T.)
The Variation of Cylinder Pressure (2000 rpm,-100 mmHg)
The Variation of Cylinder Pressure (4000 rpm,-100 mmHg)
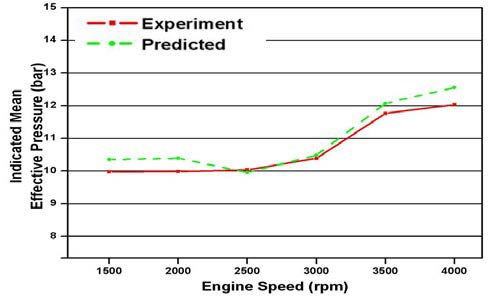
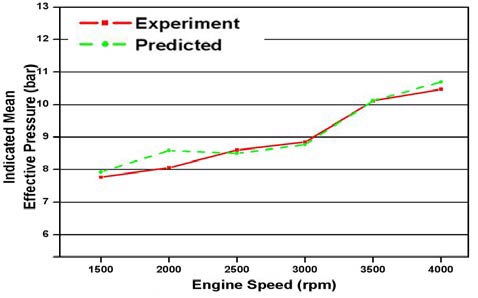
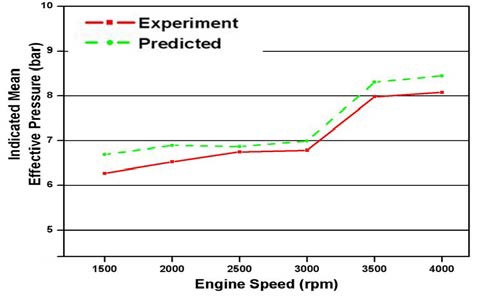
Figure 12 ~ Figure 14은 여러 가지 운전 조건에서 도시평균유효압력의 실험값과 예측값을 비교하여 도시한 것이다. 일부 운전 조건에서 도시평균유효압력의 예측값이 5 % 내외의 오차를 보이는 것을 제외하면, 대부분의 다른 운전조건에서는 3 % 이내의 정확도로서 도시평균유효압력을 계산하고 있다. 앞서의 압력-크랭크 각 선도에서 나타난 압축과정에서의 차이와 흡⦁배기 과정에 있어서의 근소한 차이는 출력 성능 인자의 예측에 있어서 우려할 만한 차이를 보이지는 않는 것으로 판단할 수 있다. 따라서 본 연구에서적용한 연소모델과 열전달 모델 및 이에 관련한 상수결정 방법들은 그 단순함에도 불구하고 대상 기관의 도시성능을 비교적 잘 나타내고 있는 것으로 볼 수 있으며 이와 같은 결정 과정은 실험 자료가 적은 기술 현장에서 유용하게 사용될 수 있을 것으로 판단된다.
Indicated Mean Effective Pressure (W.O.T.)
Indicated Mean Effective Pressure (-100 mmHg)
Indicated Mean Effective Pressure (-200 mmHg)
5. 결 론
다중 연료분사식 가솔린 기관의 성능을 예측하기 위해 AVL BOOST를 이용하여 시뮬레이션을 시행하였다. 계산 결과를 실험값과 비교, 검토한 결과를 다음과 같이 요약할 수 있다.
- (1) 흡기 및 배기 계통 주요 위치에서의 크랭크 각에 따른 관내 압력 변화는 실험값과 예측값이 전반적으로 잘 일치하고 있으며 실린더 내로의 공기 공급량도 비교적 잘 예측되고 있다. 이는 본 연구에서 적용한 흡·배기 모델링과 Noyes 식에 의한 밸브유량계수의 산정이 유용함을 나타낸다.
- (2) Wiebe 연소 모델에서 연소지속기간의 값은 실린더 최고압력의 값에 직접적인 영향을 미치며 다른 성능 인자에 미치는 영향은 크지 않다.
- (3) 열전달 보정계수를 변화시킬 경우 실린더 내 최고압력과 도시평균유효압력이 모두 영향을 받으나 도시평균유효압력의 값에 보다 직접적으로 영향을 미치고 있다.
특정 운전조건에서 도시평균유효압력을 이용하여 열전달 보정 계수를 선정하고 이를 다른 운전조건에 그대로 적용하고, 실린더 최고 압력을 이용하여 연소지속기간을 산정하고 Hire 관계식을 통해 다른 운전 조건에 확장 적용하였다. 이 결과 주요 성능 인자의 예측에 있어서 만족할 만한 결과를 얻을 수 있었다. 이 방법은 실험 자료가 적은 기술 현장에 있어서의 시뮬레이션에 유용하게 사용될 수 있을 것으로 판단된다.
Nomenclature
| a : | Wiebe parameter |
| A : | Area |
| Cd : | Discharge coefficient |
| cm : | Mean piston speed |
| cu : | Circumferential velocity |
| cv : | Constant volume specific heat |
| D : | Diameter |
| f : | Piston to head distance at ignition timing |
| h : | Enthalpy |
| ID : | Ignition delay |
| m : | Mass or Wiebe shape parameter |
| m : | Engine speed |
| p : | Pressure |
| Q : | Heat transfer |
| s : | Laminar flame speed |
| T : | Temperature |
| V : | Volume |
| x : | Mass fraction burned or distance |
| α : | Crank angle |
| αw : | Heat transfer coefficient |
| θ : | Seat angle |
Acronyms
| c : | Cylinder or Combustion |
| e : | Outflow |
| F : | Fuel |
| i : | Inflow |
| IVC : | Intake valve closure |
| o : | Motored condition |
| p : | Pipe |
| ref : | Reference condition |
| TDC : | Top dead center |
| v : | Valve |
| w : | Wall |
Acknowledgments
이 논문은 2015~2016년도 창원대학교 자율연구과제 연구비 지원으로 수행된 연구결과임.
이 논문은 정창식의 학위논문(“BOOST를 이용한 가솔린 기관의 성능해석에 관한 연구, 창원대학교 산업대학원”)을 개선한 것임.
References
-
H. S. Jang, J. W. Lee, K. K. Lee, and J. S. Choi, “Prediction of NOx emission for marine gas engine”, Journal of the Korean Society of Marine Engineering, vol. 38(no. 6), p658-665, (2014), (in Korean).
[https://doi.org/10.5916/jkosme.2014.38.6.658]
- M. Ott, “X-DF Low-pressure dual-fuel engine technology”, WinGD Licensees Conference 2015, Interlaken, (2015).
-
K C. Noh, D. I. Seol, K. M. Hu, and S. H. Kim, “Development and performance evaluation for 1.6 MW gas engine”, Journal of the Korean Society of Marine Engineering, vol. 36(no. 2), p230-237, (2012), (in Korean).
[https://doi.org/10.5916/jkosme.2012.36.2.230]
-
D. K. Lee, K. S. Yoon, S. P. Ryu, S. K. Woo, and H. G. Seong, “Study on the simulation of the intake and exhaust systems of a gasoline engine using BOOST”, Transactions of the Korean Society of Automotive Engineers, vol. 21(no. 4), p23-32, (2013).
[https://doi.org/10.7467/KSAE.2013.21.4.023]
-
R. S. Benson, W. J. D. Annand, and P. C. Baruah, “A simulation model including intake and exhaust system for a single cylinder 4-stroke Cycle S. I. engine”, International Journal of Mechanical Sciences, vol. 17(no. 2), p97-124, (1975).
[https://doi.org/10.1016/0020-7403(75)90002-8]
- R. S. Benson, The Thermodynamics and Gas Dynamics of Internal-Combustion Engines, vol. 1, Oxford, Clarendon Press, (1982).
- AVL, BOOST User’s Guide Version 2014 Theory, (2014).
-
J. I. Ghojel, “Review of the development and applications of the Wiebe function: a tribute to the contribution of Ivan Wiebe to engine research”, International Journal of Engine Research, vol. 11(no. 4), p297-312, (2010).
[https://doi.org/10.1243/14680874JER06510]
- S. D. Hires, R. J. Tabaczynski, and J. N. Novak, “The prediction of ignition delay and combustion intervals for a homogeneous charge spark ignition engine”, SAE paper 780232, (1978).
- G. Woschni, “A universal applicable equation for the instantaneous heat transfer coefficient in the internal combustion engine”, SAE paper 670931, (1967).
- J. B. Heywood, Internal Combustion Engine Fundamentals, vol. 1, New York, McGraw-Hill, (1988).
-
S. W. Park, I. S. Choi, K. C. Rho, S. P. Ryu, K. S. Yoon, “An experimental study on measurement of flow coefficient using the steady-flow test rig”, Journal of the Korean Society of Marine Engineering, vol. 36(no. 4), p423-429, (2012), (in Korean).
[https://doi.org/10.5916/jkosme.2012.36.4.423]
-
R. S. Benson, P. C. Baruah, and Ir. R. Sierens, “Steady and non-steady flow in a simple carburettor”, Proceedings of Institution of Mechanical Engineers, vol. 188, p537-548, (1974).
[https://doi.org/10.1243/PIME_PROC_1974_188_066_02]
- R. N. Noyes, Analytical Prediction of Discharge Coefficients for Engine Poppet Valves, GM Report-3376, General Motors, USA, (1980).
- S. P. Ryu, Study for Prediction of Pressure Variation in the Combustion Chamber of the Marine Diesel Engine, M.S. Thesis, Department of Mechanical Engineering, Changwon National University, Korea, (2007), (in Korean).