전산 유체 해석을 이용한 어선의 속도 성능 추정

2.1 대상선 및 해석 조건

본 연구에서 사용한 대상선의 주요 치수는 Table 1과 같다. LPP는 선미와 선수의 수선간 거리이며, TF와 TA는 각각 선수와 선미의 흘수이다. DISP는 대상선의 배수량을 나타내며, LCB는 선미 수선에서 부심까지의 거리이다.

Table 1:

Particulars of the present objective ship

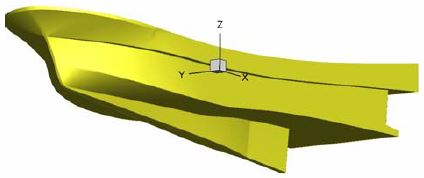
대상선의 3차원 형상은 Figure 1에 나타내었으며, 5개의 선속에 대해 각 흘수에서 저항 계산을 수행하였다. 계산 조건은 Table 2와 같다. 향후 예인 수조 모형 시험에 사용할 모형선의 축척비는 1/6.4이므로 모형선의 속도는 프루드 수의 상사성에 기반하여 정해진다.

Figure 1:

Three dimensional geometry of hull

Table 2:

Ship speeds simulated in the present study

2.2 수치 기법

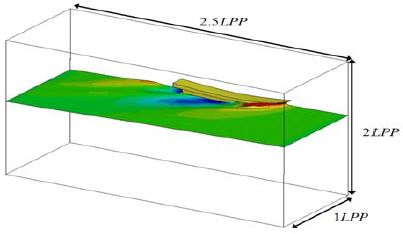
본 수치 해석은 주요 목적은 예인 수조에서 계측하는 모형선 저항을 정도 높게 예측하는 것이므로 계산 영역, 격자의 크기는 모두 모형선을 기준으로 하였다. 본 계산을 위하여 적용된 좌표계 및 계산영역은 Figure 2에서 보는 바와 같이 유동방향이 양(+)의 x축이고 선박의 우현이 양의 y축이며 중력의 반대방향이 양의 z축으로 하는 직교 우수 좌표계를 사용하였다. 좌표계의 원점은 선체 중심면과 중앙면 그리고 자유수면(free surface)이 만나는 점에 위치한다. 계산 영역은 원점에서 선수부 방향으로 1.0LPP, 선미부 방향으로 1.5LPP이며 폭 방향으로 1.0LPP 이다. 자유수면에서 수심 깊이는 1.2LPP 이며, 공기에 해당하는 영역의 높이는 0.8LPP이다.

Figure 2:

Numerical domain and coordinate system

U_i(i = 1, 2, 3)를 Reynolds 평균된 각 방향의 속도 성분으로 정하고, 유동의 지배방정식을 Reynolds 평균할 경우 연속방정식과 운동량 방정식은 다음과 같다.

또한 운동량 방정식인 Reynolds averaged Navier-Stokes 식은 다음과 같이 표현된다.

여기서 p는 Reynolds 평균 및 무차원화된 정압, RN은 선체 길이(Lpp), 모형선의 속도(V_M) 및 물의 밀도(ρ) 및 점성(μ)으로 무차원화된 Reynolds 수(R_N = ρ × Lpp × V_M/μ)이며, $$ -\overline{u_i{u}_j}$$은 단위 밀도에 대한 무차원화된 Reynolds 응력이다. Reynolds 응력에 대한 난류 종결(turbulent closure)을 위해 7-equation Reynolds stress model (Reynolds stress equations + ε equation)을 사용하였다. Reynolds stress 방정식 중에서 pressure-strain 항에 대해서는 linear model을 사용하였다. 효율적인 격자 구성을 위해 선체 표면 근처에서는 벽 함수를 이용하였기 때문에, 벽면 근처에서 계산한 난류 운동 에너지(k)로부터 벽면 마찰속도를 추정하는 벽면 처리를 적용하였다 (Park et al. 2013). 자유 수면에 대해서는 VOF를 적용하였으며, HRIC(high resolution interface cap-turing) scheme을 이용하여 공간 차분하였다. 본 연구에서는 상용 프로그램인 STAR-CCM+에서 상기의 수치 조건을 적용하여 선체 저항을 해석하였다.

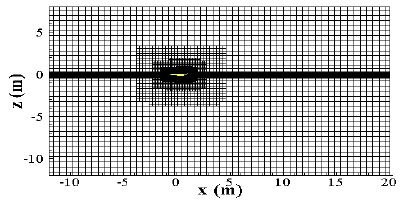
선체표면 및 공간격자 생성은 기존 연구에서 사용한 격자와 동일하게 트리머(trimmed mesh)와 경계층 격자(prism layer)를 사용하였다. 모형선 길이 6-8m 및 ±1° 이하인 동적 트림 각도에 최적화된 기존의 검증된 격자계를 사용할 경우 Figure 3에서 보는 바와 같이 약 349,265개의 격자가 생성된다. 이러한 격자계는 모형선의 크기가 작을 경우 격자수를 줄일 수 있고 경계면에서 자유수면이 반사되는 수치 오차를 줄일 수 있는 장점이 있으나, 서두에서 언급한 바와 같이 길이 2m 수준의 모형선을 적용할 경우 동적 트림의 회전 중심에서 계산 영역의 입구 경계까지 거리가 너무 멀고 자유수면에 밀집된 격자 영역이 충분하지 못하기 때문에 동적 트림이 ±1°를 초과할 경우 선체 저항이 불안정한 수치 결과를 얻게 된다.

Figure 3:

Grid system used in the previous studies

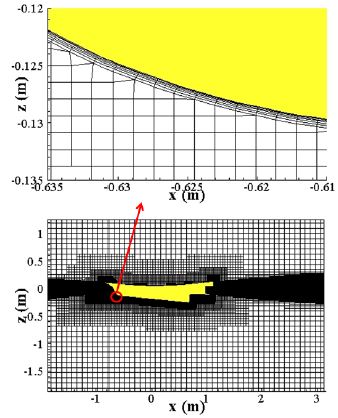
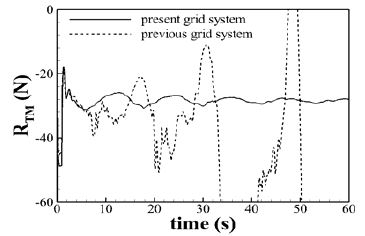
이러한 수치적 불안정성을 해결하기 위해 본 대상선의 특성에 적합한 격자계를 Figure 4에서와 같이 구성하였다. 동적 트림의 회전 중심에서 계산 영역의 입구 및 출구 경계까지 거리를 감소시키고, 동적 트림에 의해 계산 영역 전체가 ±4°까지 회전하더라도 자유수면의 위치가 밀집된 계산 영역에 포함될 수 있도록 하였다. 이러한 격자 구성을 취할 경우 선체 근처의 격자수가 증가하고, 자유수면를 모사하기 위한 수직 격자가 증가함으로써 약 354만개의 격자가 생성되는 단점이 있으나, Figure 5에서 보는 바와 같이 수치적 안정성과 정도가 개선되어 안정적인 선체 저항을 얻을 수 있는 장점이 있다. 그림에서 점선은 기존의 격자를 사용하여 수치 해석을 수행한 결과이며, 실선은 새로운 격자 시스템에서 저항 해석을 수행한 결과이다. 새로운 격자 시스템에서 선체 저항은 시간이 지남에 따라 안정적으로 수렴하는 반면, 기존 격자 시스템을 사용할 경우 선체 저항이 발산하는 것을 볼 수 있다.

Figure 4:

Grid system used in the present study

Figure 5:

Comparison of numerical convergence between the present and previous grid systems

2.3 저항 계수 계산

점성 유동해석 결과로부터 선체의 수직방향 응력과 수평방향 응력으로부터 선체에 작용하는 전저항(RTM)을 식 (3)으로부터 구할 수 있다.

여기서 S는 선체의 접수면적, CP는 압력을 속도와 밀도로 무차원화한 압력 계수, nX는 선체 표면의 법선 단위 벡터 중 선체 진행 방향 성분, Cfx는 점성 마찰 저항 벡터 중 선체 진행 방향 성분, CTM은 선체 표면에 작용하는 전저항 계수이다.

3.1 속도 및 흘수별 동적 트림

본 연구에서 사용한 Figure 4의 격자계는 대상선의 동적 트림이 ±4° 범위 내에 있을 경우 자유수면이 밀집된 격자 영역에 존재하도록 생성되었다. 따라서 설계 흘수와 밸러스트 흘수에서 Table 2의 속도 범위(Fn = 0.3738~0.8011)일 때 트림 각도가 ±4° 범위 내에 있는지를 알기 위해 동적 운항 자세를 Table 3에 정리하였다. 표에서 sinkage의 (-) 부호는 대상선이 선체에 작용하는 압력에 의해 아래로 움직이는 병진 운동을 의미하며, 트림(trim)의 (-) 부호는 부심을 중심으로 대상선의 선수부가 아래로 움직이는 선수 트림 상태을 의미한다. 표에서 알 수 있는 바와 같이 대상선의 최대 동적 트림 각도는 밸러스트 흘수, 선속은 7노트일 때 –3.3°가 되므로 본 연구에서 사용한 격자계가 유효하게 적용될 수 있다.

Table 3:

Dynamic sinkage and trim

3.2 속도 및 흘수별 전저항 계수 (CTM)

각 흘수별로 속도에 따른 전저항 계수를 계산해보면 Table 4와 같다. 전체 저항에서 압력 저항과 마찰 저항의 기여도를 함께 정리하였다. 표에서 보듯이 속도와 흘수에 따라 다소 차이는 있으나 전체 저항 중 72%~78%가 압력 저항에 기인한다. 이러한 경향은 일반적인 대형 상선과 매우 다르기 때문에 일반적인 대형 상선을 추정하는 격자나 수치 해석 기법으로는 어선의 저항을 추정하기 어려운 이유가 된다.

Table 4:

Coefficients of total resistance

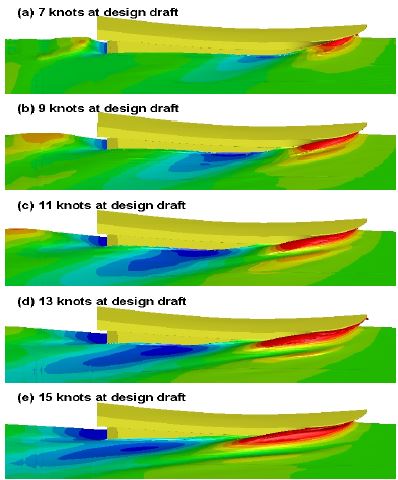
압력 저항이 크게 발생하는 원인은 선체 주변에서 발생하는 자유수면을 통해 보다 명확하게 알 수 있다. Figure 6은 설계 흘수에서 각 선속 별로 자유수면의 높이를 나타낸 그림이다. 자유수면은 물의 체적율(volume of fluid)이 0.5가 되는 면으로 추출하였으며, 자유수면의 높이는 –0.04m(파란색)부터 +0.04m(붉은색)까지 iso-contour로 표현하였다. 그림에서 보듯이 모든 속도에서 매우 높은 선수파가 발생하고 있으며 속도가 높아질수록 선수파가 더 강해진다. 이렇게 발생하는 선수파는 선수부에서 강한 압력 저항으로 작용하기 때문에 Table 4에서 보는 바와 같이 모든 속도에서 전체 저항의 72%~78%가 압력 저항에서 기인하게 된다.

Figure 6:

Wave patterns at design draft

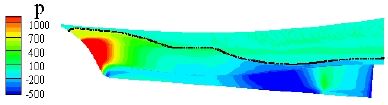
이러한 압력 저항은 선체 표면에서의 압력 값 분포로부터 자세히 추정할 수 있다. Figure 7은 계산에서 얻어진 압력(p_CFD)으로부터 식 (4)를 통해 정수 압력을 제거한 결과를 선체 표면에서 iso-contour로 표현한 그림이다.

Figure 7:

Pressure distribution on hull at 11 knots (design draft)

식에서 α_water는 각 격자에서 물의 체적율을 나타내며, ρ_water, ρ_air는 각각 물과 공기의 밀도를 의미한다. g와 z는 중력 가속도와 각 격자의 수직 방향 위치를 의미하는데, 정수 상태를 기준으로 수면 아래쪽은 음수가 되며 수면 위는 양수가 된다. 그림은 대표적으로 선속 7노트, 설계 흘수일 때 압력 분포를 보여 준다. 그림에서 압력은 –500Pa에서 1000Pa까지 나타내었으며, 검은 선은 선측 파형을 보여준다. 그림에서 보듯이 선수파에 의해 선수부에 매우 강한 압력이 작용함을 알 수 있다.

3.3 유효마력, 제동마력 및 속도 성능 추정

CFD로부터 계산된 2가지 흘수에서의 전저항(R_TM)을 이용하여 ITTC-1978 2차원 해석법에 따라 저항 해석을 수행 하였다(ITTC-1978). 유효마력(effective power, PE) 결과는 Table 5에 나타내었으며, 계수들에 대한 정의는 ITTC-1978을 참조 바란다.

Table 5:

Resistance and propulsive performance prediction employing the total resistance(RTM) based on CFD

준 추진효율 계수(ETAD, ηD)는 유사선종의 모형시험 자료로부터 Design 흘수에서는 0.60 그리고 Ballast 흘수에서는 0.61로 추정 하였다. 제동마력(brake power, BP) 추정과정에서는 마력 보정은 없는 것(CP = 1.0)으로 하였으며, 해상상태(Sea Margin)는 연안을 감안하여 0%를 사용하였다. 축 손실 계수는 1%로 하였다. 이러한 값들을 바탕으로 2가지 흘수에서 제동마력을 추정하였다. 그 결과는 Table 5에 정리하였다.