전송효율 향상을 위한 위성 및 수중 통신의 효율적인 융합 모델 연구
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 논문은 인접 심볼 간의 간섭이 발생하지 않는 최대 데이터 전송률인 Nyquist 속도 보다 빠르게 데이터를 전송하여 전송량을 증가시키는 FTN(Faster Than Nyquist) 기법을 위성 및 수중 통신의 융합 시스템에 적용하여 효율적인 송수신 모델을 제안한다. FTN 신호 전송 시 발생하는 ISI(Inter-Symbol Interference)를 최소화하기 위해 위성통신에서는 BCJR 기법을 이용한 비터비 등화기와 LDPC 복호기간의 반복으로 이루어진 터보 등화 기법을 이용하여 복호하며, 수중통신에서는 DFE 등화기와 LDPC 복호기와 연접한 터보등화 기법을 적용하여 각 노드에서의 성능 향상을 확인할 수 있었다.
Abstract
In this paper, we analyzed efficient decoding scheme with FTN(Faster than Nyquist) method that is transmission method faster than Nyquist theory and increase the throughput. Applying the FTN method to satellite and underwater communication, we proposed an efficient transceiver model. To minimize ISI(Inter-Symbol Interference) induced by FTN signal, turbo equalization algorithms that iteratively exchange probabilistic information between Viterbi equalizer based on BCJR algorithm and LDPC decoder are used in satellite communication. In others, for underwater communication, DFE equalizer and LDPC decoder are concatenated to improve performance.
Keywords:
FTN(Faster than nyquist), Turbo Equalization, LDPC codes, Satellite and underwater communication키워드:
터보등화 기법, LDPC 부호, 위성 및 수중통신1. 서 론
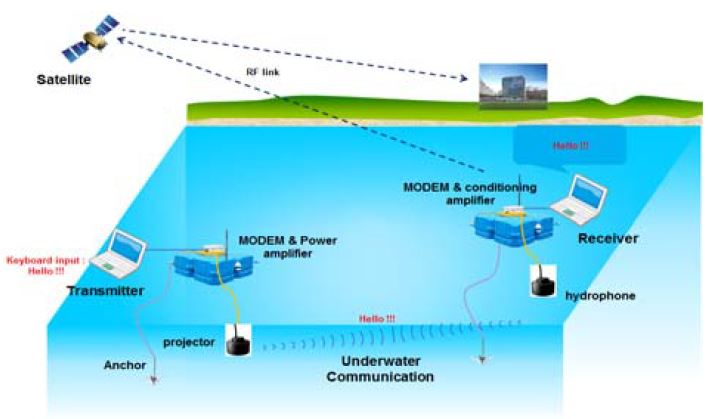
수중에서 획득한 데이터를 위성을 이용하여 지상으로 전송하기 위한 수중과 위성의 융합 시스템은 현대에 연구되어지는 관심분야이다. 더구나 Figure 1과 같이 해상 작전에서 잠수함 대 잠수함/수상함 통신, 수중 무인 잠수정 위치추적 및 원격 제어와 광해역 장거리 정보 송·수신 등의 통신 수단은 매우 중요한 요소이다. 수중에서 교환되는 정보를 위성으로 전송 또는 위성의 정보를 수중으로 전송하는 수중과 위성간의 통신 체계는 현대의 융합분야의 핵심기술이다[1]. 그러나 전파를 이용하는 위성 통신과는 달리 수중에서는 음파를 이용하여 통신을 하며, 해양의 상태, 온도, 염분도, 수심 등의 다양한 환경 요소에 따라 음파의 전달이 제한되고 육상 무선 통신에 비해 상대적으로 저주파 대역을 사용하기 때문에 대역폭이 크게 줄어들어 높은 전송률을 기대하기 어렵다.
가장 큰 문제점은 위성 통신은 표준안이 개발되어 활발히 연구 중에 있으나 수중 통신은 표준안이 확립되지 않아 수중 통신에서의 전송 방식은 채널 환경에 따라 적용 방식이 다르다. 따라서 수중 통신과 위성 통신간의 융합 모델을 확립하는 것은 매우 어렵다. 또한 수중에서의 대역폭 또한 위성 통신과는 차이가 많아 변조 방식 및 채널 부호화 방식을 각각 다르게 적용하고 있다. 따라서 본 논문에서는 위성통신에서 개발되고 있는 표준안을 수중통신에 적용시켜 수중 - 위성간의 융합 모델을 연구하고자 한다. 위성통신의 대표적인 표준안 DVB-S3(Digital Video Broadcasting-Satellite 3)은 전송효율 향상에 초점을 맞추어 제안되고 있다. 채널 부호화 방식으로는 LDPC(Low Density Parity Check) 부호를 적용시키고 변조 방식에서도 기존의 QPSK(Quadrature Phase Shift Keying), 8PSK, 16APSK에서 보다 고차변조 방식인 4/128/256 APSK 적용방식을 고려하여 표준안 채택을 위하여 제안한 기법들을 발표하고 있다[2][3]. 이러한 가운데 DVB-S3에서는 전송률 향상을 위해 주파수대역에서 주어지는 Nyquist 속도보다 빠르게 신호를 전송하여 전송률을 향상시키는 기법인 FTN(Faster Than Nyquist) 방식이 대두되고 있다[4][5].
FTN은 1/T bits/s를 전송하였을 때 이를 최적으로 수신하기 위해 1/2T Hz의 기저대역 대역폭이 요구되는 Nyquist 판별법의 한계를 넘어, 동일한 대역폭에서 Nyquist 속도보다 더 빠른 속도로 전송하여 전송효율을 증대시키는 기술로 1975년도에 Mazo[6]를 통해 제안되었고 높은 구현 복잡도로 인하여 실용화 되지 않았으나, 최근에 동일 대역폭에서 Nyquist 속도 기반의 전송 대비 전송률이 30~100% 까지 향상될 수 있음을 제시하고 있다[7][8].
수중통신에서는 다중 경로로 인한 심한 왜곡이 발생하기 때문에 수중 통신에서 전송률 향상을 위해 고차 변조 방식의 적용은 어려움이 따른다. 따라서 본 논문에서는 전송률 향상을 위해 위성통신에서 적용하는 FTN 기법을 적용하여 고전송 효율을 갖는 위성 - 수중 통신 융합 모델을 제시한다. 그러나 FTN 기법 적용으로 인한 ISI(Inter-Symbol Interference) 가 발생하여 성능 저하를 야기하는데, 이를 해결하기 DVB-S3에서는 비터비 등화기를 이용하여 LDPC 복호기와 연접한 터보 등화 기법을 시도하고 있다. 터보 등화기법은 BCJR(Bahl, Cocke, Jelinek and Raviv) 기법을 이용하여[9][10] LDPC 복호기와 연접한 터보 등화 기법을 사용하는 방식을 나타내며, 수중으로의 적용 시 성능 분석 및 효율적인 모델을 제시하여 그에 따른 융합 모델을 제시한다. 위성 전송방식에 적용되는 FTN 전송 방식을 수중 음향 통신 단말기에 융합 적용하면 수중에서도 멀티미디어 데이터와 같은 대용량 고품질 서비스를 제공할 뿐만 아니라 기술적인 측면에서 반복 터보 등화 기법을 이용한 간섭 제거 및 성능 향상을 가져올 수 있다. 따라서 본 논문에서는 실제 수중 통신 환경에서 실험을 통하여 FTN 방식을 수중으로 적용 시 성능의 효율성을 입증하였다.
2. FTN 신호 모델링
FTN 전송 방법은 주파수 대역에 의해 주어지는 Nyquist 속도보다 빠르게 신호를 전송하는 방법이다. 예를 들어 어느 정해진 시간동안 Nyquist 속도에 따라 전송하면 10000개의 데이터를 전송한다고 했을 때, FTN 방식을 사용하여 50%로 축소하면 동일한 시간동안 20000개의 데이터를 전송할 수 있다. 그로 인해 필연적으로 ISI가 발생하게 된다. 간섭된 신호의 전송신호 s(t)는 식 (1)과 같이 나타낼 수 있다.
| (1) |
여기서 an은 n시점에서 부호화된 비트열을 나타내며, h(t - nτT ) 는 저대역 필터 응답을 나타낸다. τ는 FTN으로 인해 Nyquist 속도 보다 얼마큼 빠르게 보내는 간섭 점을 나타낸다. 예를 들어 τ가 1일 때는 기존의 Nyquist 속도와 동일하게 전송하는 것을 의미하며, 이의 간섭비율은 0%이다. 간섭비율 τ′은 식 (2)와 같이 나타 낼 수 있다.
| (2) |
간섭비율은 다르게 정의하면 τ′만큼의 전송률 향상을 의미한다. 주기T 에 할당된 샘플 수 Ns에서 간섭되는 샘플 수 는 간섭비율 τ′과의 관계는 식 (3)과 같다.
| (3) |
FTN 전송 신호에 대한 수신신호는 아래 식 (4)와 같이 나타낼 수 있다.
| (4) |
p((n - k)τT ) 는 수신신호 nτ시점에서의 정합필터 값을 나타내며, n′(nτT ) 는 nτ시점에서의 잡음을 나타낸다. 이의 간섭 및 잡음으로 왜곡된 신호는 오류정정 부호화 방식을 적용하여 보상할 수 있으나 한계가 있다.
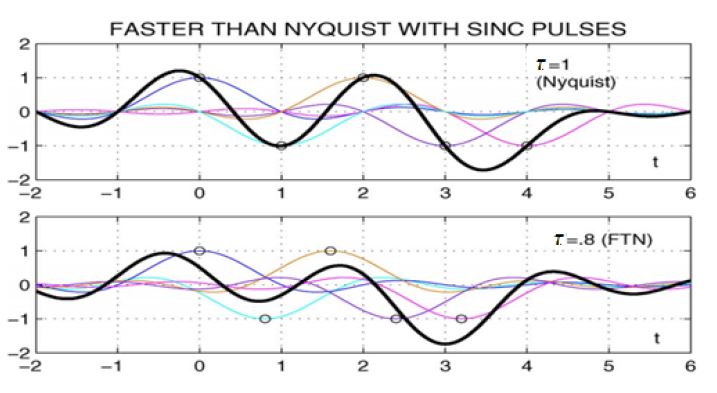
Figure 2에서 τ = 1인 경우에는 Nyquist 속도에 따라 전송되므로 ISI가 생기지 않는 것을 알 수 있다. 그러나 τ = 0.8인 경우에는 FTN으로 인해 인접 심볼들이 서로 영향을 주어 데이터의 결정 시점 마다 원으로 표시된 부분이 원 데이터에 첨가 되어 데이터에 영향을 주므로 간섭으로 인한 파형의 변화가 있음을 알 수 있다. ISI로 인해 신호의 파형이 왜곡 되지만 이를 해결할 수 있다면 동일한 시간에 20%의 전송률을 향상 시킬 수 있음을 알 수 있다. 수중 및 위성에서 ISI로 인한 왜곡된 신호를 복호 할 수 있는 효율적인 복호 모델은 3장에서 제시한다.
3. 융합 모델 요소 분석 및 성능
수중과 위성간의 융합 모델을 제안하기 위해서는 위성과 수중으로 음파를 전달하기 위한 중계기와 수중 센서와 수중에서 획득한 데이터를 위성으로 전달하기 위한 수중 중계기간의 모델이 우선적으로 정립되어야 한다. 이러한 융합 시스템의 모델을 정립하기 위해서 본 장에서는 각 노드간의 최적의 송수신 구조 및 성능 분석을 한다.
3.1 위성과 수중 중계기간의 모델 및 성능
기존의 DVB-S2 표준안에서는 복호 방식을 LDPC 부호화 방식을 적용하고 있으나 이는 2장에서 설명한 FTN 기법 적용으로 인한 ISI를 해결하기에 어려움이 있다. 따라서 DVB-S3에서는 FTN 적용으로 인한 ISI를 제거하기 위해서 비터비 등화기를 이용하여 LDPC 복호기와 연접한 터보 등화 기법을 시도하고 있다. 적용되는 비터비 등화기는 이미 널리 알려진 것과 같이 경판정 된 비트가 출력되므로 이를 LDPC 복호기의 입력으로 사용되면 성능 저하를 초래한다. 따라서, BCJR 알고리즘을 이용하여 비터비 등화기를 구성하였다. 비터비 등화기에서 출력되는 연판정 값을 LDPC 복호기에 입력하여 반복구조로 구성한 터보 등화 기법을 사용하는 방식이다. 이는 Figure 3과 같으며, Kim et al. [11]에서 제시된 알고리즘 및 성능을 간략히 분석한다.
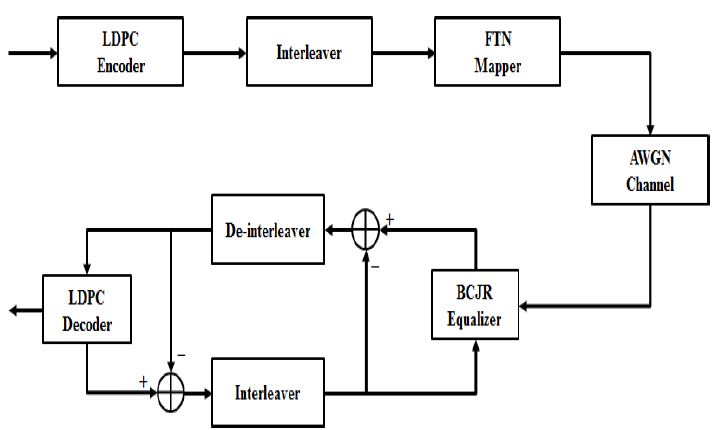
Structure of encoder and decoder included Viterbi Equalizer based on BCJR method and Turbo Equalization
Figure 3의 블록도에서 LDPC 부호화기로 데이터를 부호화시키고 인터리버를 통과한 뒤 FTN mapper를 이용하여 τ′만큼 간섭비율을 발생하여 AWGN(Additive White Gaussian noise) 채널을 통과한다. τ′만큼 간섭비율의 의미는 τ′만큼 전송률이 증가됨을 의미한다. 그리고 BCJR 기법을 이용한 비터비 등화기를 이용하여 FTN으로 인한 ISI를 보상해준 다음 디인터리빙하고 LDPC 복호기를 이용해 복호한다. 그리고 반복을 통하여 성능을 향상시킨다. AWGN 통과 전의 FTN에 의한 ISI만을 포함하는 데이터는 수신 측에서 예측이 가능하다. 그 이유는 τ′에 따라 ISI로 인해 어느 정도의 값을 가지게 되는지 알 수 있기 때문이다. BCJR기법을 이용한 비터비 등화기는 이 데이터를 이용하여 BM(Branch Metric)을 구하고 BSM(Backward State Metric), FSM(Forward State Metric), 그리고 LLR(Log Likelihood Ratio)을 구하여 ISI를 보상한다[12][13]. Figure 3의 모델에서 FTN 신호를 AWGN 채널을 통과시킨 뒤 비터비 등화기 없이 오로지 LDPC 복호기만을 이용하여 복호하였을 때의 시뮬레이션 결과는 다음 Figure 4와 같다.
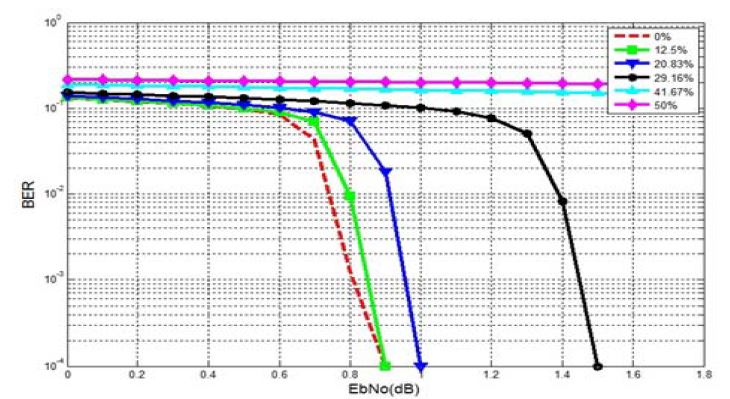
Figure 4를 보면 간섭비율이 10% 일 때는 0%와 성능이 거의 비슷하며, 대략 20% 정도의 FTN의 성능은 0.1dB 정도로 성능 차이가 크게 나지 않지만 그 이상의 FTN을 사용하면 성능이 악화되다가 약 40%이상으로 축소하게 되면 과도한 ISI로 인해 Eb/No가 커지더라도 복호하지 못하는 것을 알 수 있다. 즉, ISI가 성능에 큰 영향을 끼치게 되므로 이를 보상해주는 것이 필요하다.
본 논문에서는 이를 보상하기 위해 BCJR 기법을 이용한 비터비 등화기를 사용한다. BCJR 기법의 비터비 등화기 성능을 측정하기 위한 시뮬레이션 파라미터는 다음과 같다. LDPC 부호화율은 1/2이며 DVB-S2 규격에 따라 부호화 입력 비트 수는 32400개, 부호화된 비트 수는 64800 개로 설정하였다. 필터는 roll-off factor 가 0.35, 샘플링 간격이 24, 필터 탭이 1인 SRRC(Square Root Raised Cosine filter) 필터를 사용했다. 그리고 반복 수는 시뮬레이션 결과 최적이었던 내부 반복(LDPC 복호기) 60회, 외부반복 (터보 등화 기법) 4회로 고정하였다. 여기서 τ′ 이 12.5%는 필터의 샘플수 Ns가 24개 이므로 간섭되는 샘플수 는 3임을 의미한다.
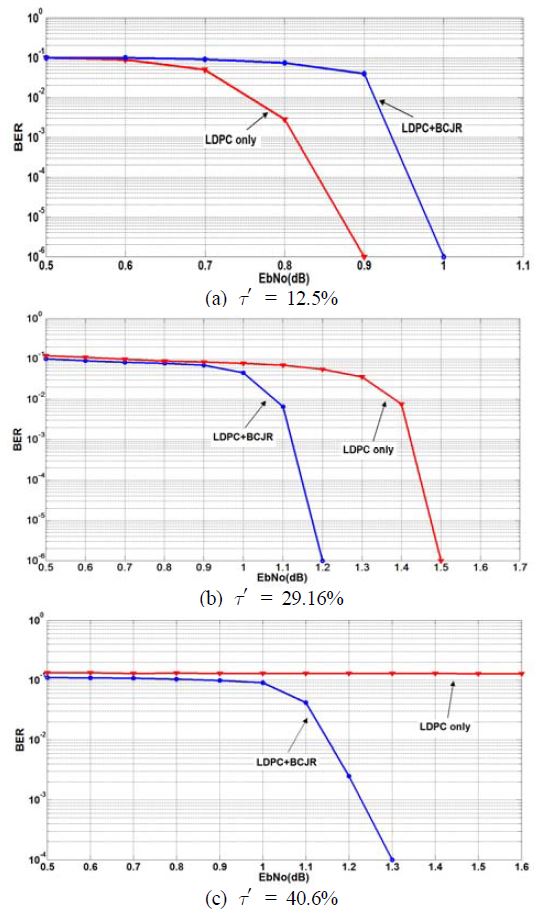
Figure 5는 τ′에 따른 BCJR등화기와 LDPC 복호기를 적용하여 Figure 3과 같이 본 논문에서 제시한 성능과 LDPC 복호기만 적용한 경우의 성능 비교 그림이다. τ′ = 12.5% 인 경우에는 본 논문에서 제시한 BCJR등화기를 적용 할 때, 0.1dB의 손실이 발생하는데 이는 BCJR 등화기에서 BM을 계산하여 복호 시 수신신호와 branch symbol간의 거리를 구하는 차이가 크지 않아 오히려 잘못된 복호 값이 출력되어 LDPC 복호기로 입력되기 때문이다. 그러나 τ′이 어느 정도 큰 값이 입력되면, branch symbol간의 거리를 구하는 차이가 커져 BCJR 등화기의 성능이 효과를 나타낸다. τ′이 30%의 경우 0.2dB 향상되며, τ′이 40% 일 때는 성능의 차이가 두드러짐을 알 수 있다. Figure 4 의 τ′ = 0%와 비교하면 τ′ = 40%의 경우 FTN을 적용시키지 않은 시스템에 비해 성능이 약 0.4dB 손실을 가져오지만 전송률을 약 두 배 가까이 높임으로써 고속으로 전송 시에는 유리한 장점을 갖고 있다.
3.2 수중센서와 수중 중계기간의 모델 및 성능
현대 통신의 융합체계의 핵심인 수중과 위성간의 연계시스템을 구성할 때, 위성통신의 전송 방식을 수중에서도 동일하게 적용하여야 한다. 따라서 수중통신의 전송률 향상을 위하여 FTN 기법을 적용하였다. 수중에서 전파는 급격한 감쇠특성을 갖기 때문에 수중에서의 무선통신에는 위성 통신과는 달리 음파를 이용하여 통신을 하게 된다. 음향 채널의 경우 전달 과정에서 잔향 및 다중경로 등에 의해 크게 왜곡되며 ISI를 야기하여 통신 시스템의 성능을 저하시키게 되며, 음파 통신의 단점은 낮은 대역폭으로 인해 전송률을 증가시킬 수 없다[14][15]. 이에 본 논문에서는 다중 경로 환경에서 원활한 통신과 함께 수신 신호의 성능을 향상시키기 위하여 낮은 SNR(Singnal to Noise Ratio)에서 우수한 성능을 보이며, 다중 경로로 인해 왜곡된 데이터를 보상하기 위한 기법인 결정 궤환 등화기 (DFE : Decision Feedback Equalizer) [16][17]가 결합된 터보 등화기구조를 고려하였다. 또한, 고 전송률의 문제를 해결하기 위해 앞서 연구한 FTN 기법을 경북 문경시 경천호에서 실제 수중 실험을 통하여 성능을 비교 분석하였다.
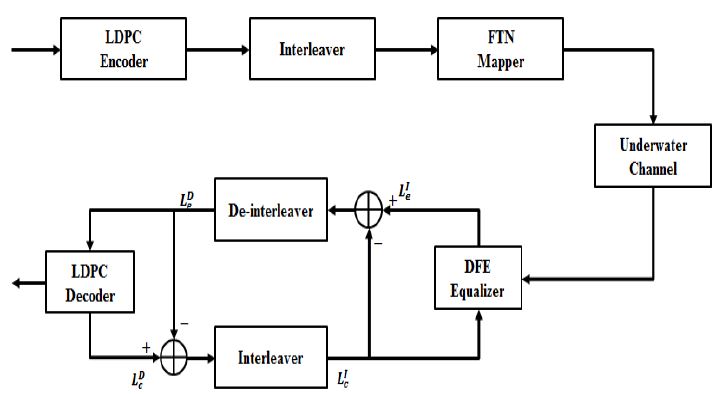
실제 수중 통신 실험 시, 열악한 수중 채널 환경에 의해 무선 통신에서와 같이 이미 알고 있는 BM 값을 이용한 BCJR 등화기를 사용할 수 없다. 그러므로 적절한 τ′ 값을 적용하고, 이에 따른 ISI를 수중에서 발생한 다중 경로 채널에 의한 ISI에 추가된 ISI로 생각하여 BCJR 등화기가 아닌 결정 궤환 등화기를 이용하여 수중에서 발생하는 ISI와 FTN으로 인한 ISI를 보상한다. 등화기에 추정된 값을 업데이트를 하기 위해서 LDPC 복호기의 외부 정보 값을 이용하였다. 본 논문에서는 Figure 6과 같이 기존의 BCJR 등화기가 아니라 결정 궤환 등화기를 갖는 터보 등화기를 고려하였다.
기저대역으로 변환한 후 LeI 는 결정 궤환 등화기의 출력값으로 수신 신호로부터 등화기에서 추정된 extrinsic 값이다. y[k]를 k시점에서의 등화기 입력 값이라 하면, 등화기의 출력은 다음 식 (5)와 같이 정의할 수 있다.
| (5) |
Cj [k], bi [k]는 k시점에서의 포워드 및 백워드 탭 계수이며, 는 성상도 상에서 LeI [k]에 가장 가까운 점들인 slicer 출력 값이다. 결정 궤환 등화기의 출력으로부터 추정된 LeI [k]와 slicer 출력 값인 의 오차를 이용하여 피드백을 통하여 결정 궤환 등화기의 출력 오차를 줄이는 계수 값인 ci [k + 1], bj [k + 1]을 갱신하기 위하여 사용된다. 외부정보 값 LcD는 복호기의 출력 값으로써 사후 확률 값을 계산하여 0 또는 1의 오류 값을 보정할 수 있는 값이다. 이러한 LcD와 LeD 의 차이 값을 인터리빙한 LcI 가 결정 궤환 등화기에 입력된다. LcI 를 업데이트 하여 오류 값을 보정하는 방법을 취하게 되는데, 반복횟수가 늘어남에 따라 업데이트 하는 오류 보정 값이 송신하고자 하는 원 신호에 가깝게 되어 성능이 향상되게 된다.
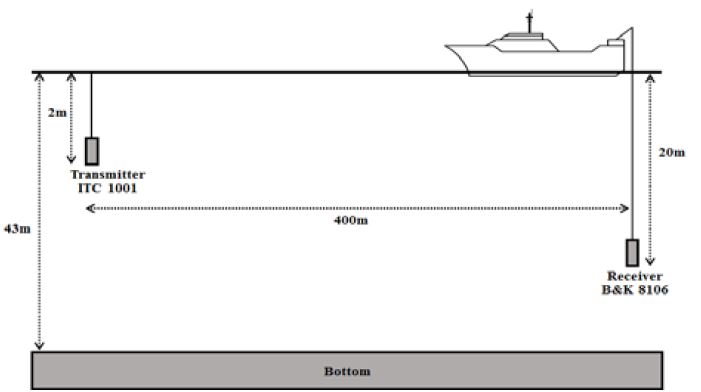
Figure 7과 같은 환경에서 실제 수중 실험을 수행하였다. 송신기로는 ITC 1001을 사용하였고 수신기로는 B&K 8106을 사용하였다. 실험은 경북 문경시 경천호에서 수행되었다. 실험 시기는 2015년 5월말로 수면상태는 바람에 의한 파도가 있었으며 송수신기 사이의 거리는 최대 400 m로 하였다. 그리고 송신기는 수면 아래 2 m, 수신기는 20 m 아래 위치하였다. 반송파 주파수와 샘플링 주파수는 각각 16 kHz 및 192 kHz로 하였으며, 전송률은 1 Kbps로 하였다.
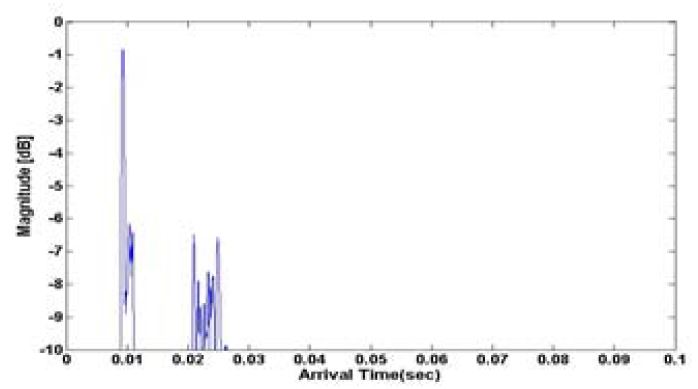
Figure 8은 실험 해역에서 측정한 채널 전달 특성을 나타낸 것이다. 측정을 위해 약 2 kHz 대역폭을 갖는 0.2 sec 길이의 LFM (Linear Frequency Modulation) 신호를 주기적으로 약 1000회 가량 송신하였다. 그림은 송수신된 LFM 신호의 상관관계를 이용하여 모델링 한 것으로 다중경로에 따른 영향을 받는 것을 확인할 수 있다. 이는 수면에 반사되는 반사파 그리고 바닥에서 반사되어 들어오는 신호들이 있다는 것을 의미한다.
수중 통신에서 또한 고 전송률을 얻기 위한 방식으로 앞서 설명한 FTN 전송 기법을 적용하여 실제 수중 통신 실험을 통해 성능을 비교분석한다. 본 논문에서는 수중 통신에는 τ′ 값을 10%와 30%를 설정하여 실험을 진행하였다.
Table 1은 수중 통신 환경에서 FTN 신호 처리 기법을 사용한 시스템의 오류 횟수를 나타낸다. 먼저 τ′ = 30% 인 FTN 기법을 적용하였을 경우, 수신된 신호인 LDPC부호화된 비트 64800 비트 중 bit 중 13,219 비트의 오류가 발생하였고, 등화기를 통해 다중경로에 의한 ISI를 보상하면 7,776 비트, 그리고 Iteration 1회에 777비트, Iteration 2회에 error free가 됨을 알 수 있었다. 그리고 τ = 10% 인 FTN 기법을 적용하였을 경우에도 오류 개수 차이는 생기더라도 2회 반복시 error free가 됨을 알 수 있었다. 이 같은 결과는 FTN 신호처리 기법 또한 고 전송률을 요구하는 수중 통신에 매우 효과적으로 작용함을 알 수 있다.
수중 채널이 시변하기 때문에 수신 신호에 발생한 오류의 양이 달라서 완벽한 비교는 할 수 없지만, 고 전송률을 달성함에 있어서 FTN 신호 처리 기법이 효과적으로 작용하는 것은 성능을 통해 쉽게 알 수 있다.
4. 고전송 효율을 갖는 수중 및 위성 융합 모델 제시
본 장에서는 이전의 3장과 4장에서 연구된 결과를 토대로 효율적인 수중 및 위성의 융합 모델을 제시하고자 한다. 수중에서 획득된 정보를 위성으로 전송 또는 위성의 정보를 수중으로 전송하는 수중과 위성간의 통신 체계에 대한 기본 블록도는 Figure 9와 같다.
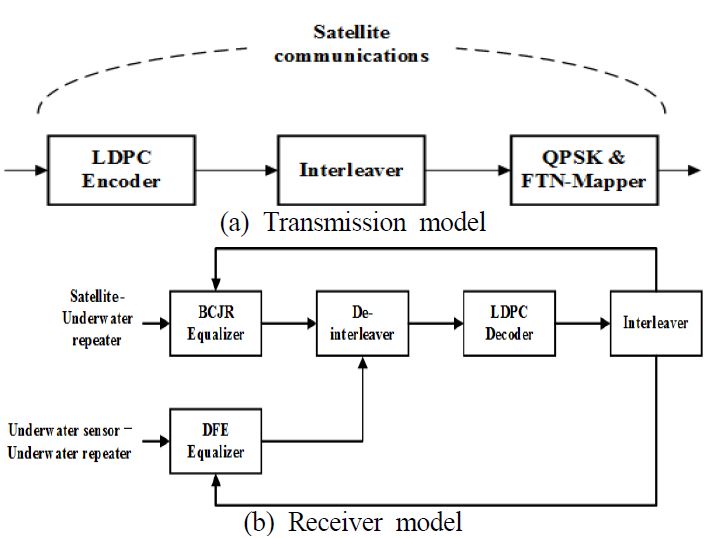
수중 중계기의 역할은 위성으로 전송된 신호를 수중으로 전송하기 위한 전파를 음파로 변환시키는 역할을 한다. 또는 수중에서 획득된 정보를 전파로 변환하여 위성으로 전송하는 역할을 한다. Figure 9와 같이 수중과 위성간의 연계시스템을 구성할 때, 위성통신의 전송 방식을 수중에서도 동일하게 적용하였을 때 각 부분에 대한 블록도는 Figure 10과 같다.
Figure 10 (a)는 수중 및 위성 통신의 융합 모델의 송신부로 위성과 수중에서 동일한 송신 구조를 갖는다. 송신부에서는 LDPC 부호화기로 데이터를 부호화시키고 인터리버를 통과한 뒤 QPSK 변조 시킨 후 FTN mapper를 이용하여 간섭 비율을 발생하여 데이터를 전송한다. Figure 10 (b)의 수신부의 구조는 위성과 수중 중계기, 수중센서와 수중 중계기로 나눌 수 있다. 위성과 수중 중계기를 통한 통신에서는 FTN 적용으로 인한 ISI를 제거하기 위해 BCJR 알고리즘을 이용한 터보 등화기법을 사용하고, 수중센서와 수중중계기에서는 결정 궤환 등화기를 사용한 터보 등화기법을 사용하여 다중 경로 채널에 의한 ISI와 FTN으로 인한 ISI를 보상한다. ISI를 보상한 뒤 디인터리빙하고 LDPC 복호기를 이용해 복호한다. 복호 된 데이터를 다시 인터리빙하고 등화기에 입력하고 이를 반복하여 성능을 향상시키는 구조이다.
5. 결 론
수중에서 획득한 데이터를 위성을 이용하여 지상으로 전송하기 위한 수중과 위성의 융합 시스템은 해상 작전에서 잠수함 대 잠수함/수상함 통신, 수중 무인 잠수정 위치 추적 및 원격 제어와 광해역 장거리 정보 송·수신 등에 활용되는 매우 중요한 요소이다. 수중에서 교환되는 정보를 위성으로 전송 또는 위성의 정보를 수중으로 전송하는 수중과 위성간의 통신 체계는 현대의 융합분야의 핵심기술이다. 그러나 위성 통신 분야와는 달리 수중 통신 분야는 음파를 이용하여 성능 및 전송 효율 관점에서는 아주 미비하게 연구되고 있으며, 표준안 자체도 이루어지지 않는 실정이다. 따라서 본 논문에서는 DVB-S3 표준안에 고전송률을 위한 FTN 적용을 위성과 수중의 융합 시스템으로 적용하여 최적의 송수신 모델을 제시하였다. 비터비 등화 모델을 BCJR 기법을 이용하여 LDPC 복호기와 연접한 터보 등화 기법을 구성하여 FTN 신호에 대한 복호 모델을 제시하였으며, 이를 수중에서도 효율적임을 실험을 통하여 입증하였다. 위성 통신의 경우에는 다중경로가 발생하지 않아 FTN으로 인한 간섭을 보상하는 BCJR 등화기를 이용한 터보 등화 구조가 최적이며, 수중에서는 다중 경로 환경에서 원활한 통신과 함께 수신 신호의 성능을 향상시키기 위하여 다중 경로로 인해 왜곡된 데이터를 보상하기 위한 기법인 결정 궤환 등화기가 결합된 터보 등화기 구조를 사용하였다. 향후 전송률 향상을 위한 위성과 수중 통신의 융합시스템에서 FTN 기법이 유용하게 사용할 수 있으리라 사료된다.
Acknowledgments
본 연구는 2015년도 정부(교육부)의 재원으로 한국 연구재단의 지원을 받아 수행된 기초 연구 사업입니다.(NRF-2015R1D1A1A01060931)
References
- U. S. Kim, “Concept of tactical data link employment and next C4ISR system”, The Quarterly Journal of Defense Policy Studies, p49-83, (2006), (in Korean).
-
D. J. C. Mackay, and R. M. Neal, “Near shannon limit performance of low-density parity-check codes”, Electronics Letters, 32, p1645-1646, (1997).
[https://doi.org/10.1049/el:19961141]

-
I. Lee, D. Chang, and D. Oh, “Multi-level modulation LDPC decoding algorithm for new generation DVB-S2 system”, Proceedings of the 24th AIAA International Communications Satellite Systems Conference, p1-4, (2006).
[https://doi.org/10.2514/6.2006-5464]

-
A. D. Liveris, and C. N. Georghiades, “Exploiting faster-than-Nyquist signaling”, IEEE Transactions on Communications, 51(9), p1502-1511, (2003).
[https://doi.org/10.1109/TCOMM.2003.816943]

-
F. Rusek, and J. B. Anderson, “Multistream faster than nyquist signaling.”, IEEE Transactions on Communications, 57(5), p1329-1340, (2009).
[https://doi.org/10.1109/TCOMM.2009.05.070224]

-
J. E. Mazo, “Faster than nyquist signaling”, Bell System Technical Journal, 54(8), p1451-1462, (1975).
[https://doi.org/10.1002/j.1538-7305.1975.tb02043.x]

-
D. Dasalukunte, F. Rusek, and V. Öwall, “An iterative decoder for multicarrier faster-than-Nyquist signaling systems”, Proceedings of the 2010 IEEE International Conference on Communications (ICC), 1(5), (2010).
[https://doi.org/10.1109/ICC.2010.5502554]

-
A. Prlja, and J. B. Anderson, “Reduced-complexity receivers for strongly narrowband intersymbol interference introduced by faster-than-Nyquist signaling”, IEEE Transactions on Communications, 60(9), p2591-601, (2012).
[https://doi.org/10.1109/TCOMM.2012.070912.110296]

-
L. Bahl, J. Cocke, F. Jelinek, and J. Raviv, “Optimal decoding of linear codes for minimizing symbol error rate”, IEEE Transactions on Information Theory, IT-20(2), p284-287, (1974).
[https://doi.org/10.1109/TIT.1974.1055186]

-
J. B. Anderson, A. Prlja, and F. Rusek, “New reduced state space BCJR algorithms for the ISI channel”, Proceedings of the IEEE International Symposium on Information Theory, p889-893, (2009).
[https://doi.org/10.1109/isit.2009.5205622]

-
T. H. Kim, I. K. Lee, and J. W. Jung, “A study on efficient viterbi equalizer in FTN channel”, Journal of Korea Institute of Information and Communication Engineering, 18(6), p1323-1329, (2014), (in Korean).
[https://doi.org/10.6109/jkiice.2014.18.6.1323]

-
C. Douillard, M. Jezequel, C. Berrou, A. Picart, P. Didier, and A. Glavieux, “Iterative correction of intersymbol interference: turbo equalization”, European Transactions on Telecommunications, 6(5), p507-511, (1995).
[https://doi.org/10.1002/ett.4460060506]

-
J. B. Anderson, and A. Prlja, “Turbo equalization and an M-BCJR algorithm for strongly narrowband intersymbol interference”, Proceedings of the 2010 International Symposium on Information Theory and its Applications (ISITA), p261-266, (2010).
[https://doi.org/10.1109/ISITA.2010.5648949]

-
D. B. Kilfoyle, and A. B. Baggeroer, “The State of the Art in Underwater Acoustic Telemetry”, IEEE Journal of Oceanic Engineering, 25(1), p4-27, (2000).
[https://doi.org/10.1109/48.820733]

-
M. Stojanovic, J. Catipovic, and J. Proakis, “Phase coherent digital communications for underwater acoustic channels”, IEEE Journal of Oceanic Engineering, 19(1), p100-111, (1994).
[https://doi.org/10.1109/48.289455]

-
K. Berberdis, T. Rontogiannis, and S. Theodoridis, “Efficient block implementation of the LMS based DFE”, Proceeding of the 13th International Conference on Digital Signal Processing, 1, p143-146, (1997).
[https://doi.org/10.1109/ICDSP.1997.627995]

-
J. Salz, “Optimum mean-square decision feedback equalization”, Bell System Technical Journal, 52(8), p1341-1373, (1973).
[https://doi.org/10.1002/j.1538-7305.1973.tb02023.x]