반복제어기법을 이용한 무궤도 이동랙 동기화제어기 설계

1. 서 론

정보화·과학화 사회로 급격한 변화가 이루어지는 21세기는 “디지털 혁명”시대라 할 만큼 IT(Information Technology) 기술이 급속히 발전을 하고 있다. 물류 산업에서도 정보기술을 기반으로 하는 무인자동화시스템의 정착이 빠르게 진행되고 있으며 이를 통해 물류비용을 최소화하여 보다 싸게, 좀 더 빠르게 서비스하기 위한 물류관리체계가 발전되고 있다.

이와 같은 물류관리체계의 발전은 증가하는 인터넷 쇼핑 및 홈쇼핑의 다품종 소량 주문에 신속함과 정확도에 부흥하고 있으며, 의약품 등 고부가가치 물류 서비스에 대한 수요에 크게 기여하고 있다. 그러나 물류관리체계의 하드웨어인 대부분의 첨단장비 및 물류 설비는 고가의 수입제품에 의존하고 있는 실정이다.

최근 우리나라에서도 화물의 다양성 및 입출고의 다빈도를 고려한 고속화, 유연화, 경량화에 대한 물류작업 속도 향상 기술 실현의 필요성이 증대되고 있다. 또한, 제품을 보관하는 기능 외에 다양한 제품의 저장, 분류 및 입출고의 정확성과 신속성까지 겸비한 종합시설로의 발전이 요구되고 있다. 이러한 시설을 통해 보관창고에서 운영 인력을 50% 절감시키는 효과와 보관효율 향상으로 40% 면적절감 효과를 가져오고 있다[1].

현재, 고정식 선반으로 인해 공간효율이 낮아지는 단점이 최근 부각되고 있으며, 일본, 유럽 및 국내 등에서는 일부 관련 제품을 출시하고 있지만 물류창고에서 활용 사례는 아직 많지 않다. 또한 국내에서 판매되는 전동식 이동랙은 단순하게 레일에 전후 이동용 모터 및 관련 안전장치 부착으로 한정된 경우가 많다.

이에, 본 연구에서는 다양한 형태로 설치가 가능한 무궤도 이동랙에 대하여 구조 및 상태를 분석하고 이를 통하여 수학적 모델링을 통해 해당 시스템이 가지고 있는 특성을 확인한다. 이동랙의 수학적인 모델링을 위하여, 팔레트 3단 적재형을 가정하고 화물의 무게, 이동랙 베이스 무게 및 관련사항을 고려하여 선형미분방정식 및 상태방정식을 도출하도록 한다.

이후에는 이동랙에 대한 동기화 제어기 설계를 구성하기 위해 파라미터 변동에 대해 강건한 강인 서보 제어계를 구성하여 시뮬레이션 검토를 행하도록 한다. 또한 이동랙의 좌측과 우측모터의 동기화 주행제어를 위한 반복제어계를 설계하여 시뮬레이션 검증을 한다. 이후, 서보제어계와 반복제어계를 이용한 동기화제어 알고리즘을 블록선도로 제안하고, 시뮬레이션 및 실험을 통하여 유효성을 입증하도록 한다.

2. 이동랙 모델링

2.1 이동랙 모델

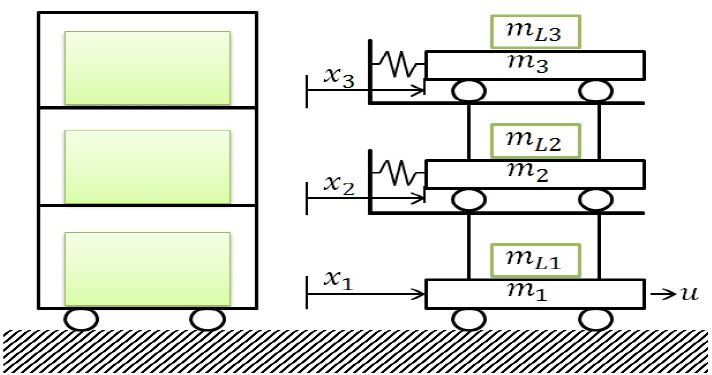
본 연구에는 3단 이동랙으로서 구동부 및 동력 전달부는 이동랙 베이스에 위치하고 있으며, 상부의 랙은 화물적재로 인하여 파라미터가 크게 변동되고 있다.

본 이동랙 모델링은 실제로 사용되고 있는 이동랙을 기준으로 설계되어진 무궤도 이동랙의 구조 방식으로서, 상부 랙의 재질을 통해 탄성계수를 계산하고 이를 적용하여 전체적인 모델링을 행한다.

이동랙의 개념적 모형 및 수학적 도식화는 Figure 1에 나타낸다. 이동랙의 수학적 모델링에서는 미분방정식을 이용하여 동적인 특성을 통하여 미분방정식으로 식 (1)과 같이 나타낼 수 있다[2]-[4].

이때, 이동랙의 베이스 모듈 및 각 층의 랙 무게 그리고 각 층에 적재된 화물의 무게를 고려하며 높이와 이동랙의 재질에 따른 탄성계수를 고려하였다.

Figure 1:

Simplified 2D drawing and it's the modeling of mobile rack

$\[ \begin{array}{c}{m}_{1L3}\ddot{x_1}+k\left(x_1-x_2\right)+B\dot{x_1}=u\hfill \\ m_{2L3}\ddot{x_2}+k\left(x_2-x_1\right)+k\left(x_2-x_3\right)=0\hfill \\ m_{3L3}\ddot{x_3}+k\left(x_3-x_2\right)=0\hfill \end{array} \]$

(1)

여기서, m_1L3 = m₁ + m_L1 + m₂ + m_L2 + m₃ + m_L3 , m_2L3= m₂ + m_L2 + m₃ + m_L3, m_3L3 = m₃ + m_L3 , $$ k=2\left(\frac{3EI}{L^3}\right)$$이며, E 는 수직구조물 재료의 탄성계수이며 I 는 단면 2차 모멘트를 나타낸다. 이때, $$ I=\frac{d_2{d}_1^3-\left(d_2-d_t\right){\left(d_1-d_t\right)}^3}{12}$$,d₁ = d₂ 은 단면길이를 나타내며 d_t 는 두께를 나타낸다.

2.2 이동랙 상태방정식

상기의 미분방정식을 상태방정식으로 나타내면 식 (2)과 같이 나타낼 수 있다[5][6].

$\[ \begin{array}{c}\dot{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right)\hfill \\ y\left(t\right)=Cx\left(t\right)\hfill \end{array} \]$

(2)

여기서,

$$ \begin{array}{cc}A=\left[\begin{array}{cc}\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}& \begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\\ \begin{array}{ccc}\frac{-k}{m_{1L3}}& \frac{k}{m_{1L3}}& 0\\ \frac{k}{m_{2L3}}& \frac{-2k}{m_{2L3}}& \frac{k}{m_{2L3}}\\ 0& \frac{k}{m_{2L3}}& \frac{-k}{m_{3L3}}\end{array}& \begin{array}{ccc}\frac{-B}{m_{1L3}}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\end{array}\right],\hfill & B=\left[\begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ \begin{array}{c}1\\ \frac{1}{m_{1L3}}\\ 0\end{array}\end{array}\right]\\ C=\left[\begin{array}{cc}\begin{array}{ccc}1& 0& 0\end{array}& \begin{array}{ccc}0& 0& 0\end{array}\\ \begin{array}{ccc}0& 1& 0\end{array}& \begin{array}{ccc}0& 0& 0\end{array}\\ \begin{array}{ccc}0& 0& 1\end{array}& \begin{array}{ccc}0& 0& 0\end{array}\end{array}\right],\hfill & x=\left[\begin{array}{c}\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\\ \begin{array}{c}\dot{x_1}\\ \dot{x_2}\\ \dot{x_3}\end{array}\end{array}\right]\end{array}$$

본 연구에서의 시뮬레이션 및 제어계 설계를 위하여 대상으로 하는 이동랙의 파라미터를 Table 1과 같이 고려한다.

Table 1:

Parameters of mobile rack

3. 동기화 제어기 설계

물류센터에서는 작업 스케쥴에 의하여 여러 가지 상태의 화물 적재가 이루어 질 수 있다. 화주의 요구에 의해 이동랙의 크기도 각각 다를 것이며 이동랙의 형태와 적재되는 적재물의 무게가 변할 수 있다. 또한 모듈별로 구성된 이동랙을 작업 스케쥴러에 의해 여러 개의 이동랙을 상호 동기화시켜 동시에 이동시켜야 할 필요성도 있다.

이때 각 이동랙에 고전적인 고정된 제어계를 설계하여 상호 동기화를 시키고자 한다면, 각 이동랙의 파라미터 변화폭(하중 변화)이 너무 커서 서보제어계로 제어가 어려울 수 있다[7].

한편으로 GA 기반의 슬라이딩 모드 제어를 이용한 동기화제어기법이 연구되었으나[8], 프로그램의 간소화 등을 고려하여 본 연구에서는 파라미터 변화가 큰 경우에도 동기화제어가 가능하도록 강인서보계와 반복제어계를 이용한 동기화제어기를 제안하고자 한다. 이를 위해 우선 강인서보계 설계 및 반복제어계를 구성하고, 이를 이용한 동기화 제어기를 설계하고자 한다.

3.1 강인 서보계 설계 및 시뮬레이션

우선 적재화물의 변동에 대해서 강건성을 지닐 수 있는 강인서보계를 구성하고자 한다.

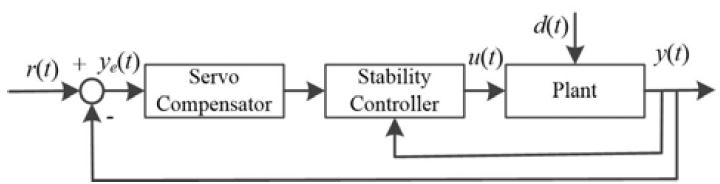
강인서보계 설계법은 그 루프내에 목표 입력이나 외란 입력의 발생 기구에 대한 모델(내부모델)을 포함하고 있어야 하며, 본 연구에서는 강인서보계를 Figure 2와 같이 구성하도록 한다[9].

Figure 2:

Servo System considering parameter variations

[정리 1][9]

가제어성 및 가관성을 만족하는 n차 m 입력 p 출력 선형시불변시스템 제어대상에 대하여 임의의 정수 l_i(≧ 0; i = 1,⋯,p)에 대하여 [l₁ ⋯ l_p ]형 제어계가 구성가능하기 위한 필요충분조건은 다음 식을 만족하는 것이다.

$\[ rank\left[\begin{array}{cc}A& B\\ C& 0\end{array}\right]=n+p \]$

(3)

상기 정리1을 만족하는 경우에, 강인서보보상기는 다음과 같이 구해진다.

본 연구에서의 이동랙은 상기 [정리 1]을 만족하므로, 다음과 같은 절차에 의해 강인서보계를 설계할 수 있다[9].

[Step 1] 확대계를 구한다. 평가함수 Q_e 및 R_e를 구한다.

$\[ \begin{array}{cc}\begin{array}{cc}{A}_e=\left[\begin{array}{cc}A& B\\ 0& 0\end{array}\right],& B_e=\left[\begin{array}{c}0\\ I_m\end{array}\right],\end{array}& \begin{array}{cc}{D}_e=\left[\begin{array}{c}{I}_n\\ 0\end{array}\right],& C_e=\left[\begin{array}{cc}C& 0\end{array}\right]\end{array}\end{array} \]$

(4)

[Step 2] 평가함수 하중계수 Q_e 및 R_e를 설정한다. 여기서 Q_e는 (n + m) × (n + m)의 반정정대칭행렬, R_e는 m × m 대칭행렬로 정의하며 Q_e = C_e^TC_e로 둘 수 있다.

[Step 3] 리카치방정식을 푼다

$\[ A_e^T{P}_e+P_e{A}_e+Q_e-P_e{B}_e{R}_e^{-1}{B}_e^T{P}_e=0 \]$

(5)

[Step 4] 최적게인 F_e를 구한다.

$\[ F_e=R_e^{-1}{B}_e^T{P}_e \]$

(6)

[Step 5] 최적 제어게인 K₁과 K₂를 구한다.

$\[ F_e{Z}^{-1}=\left[\begin{array}{cc}{K}_1& K_2\end{array}\right] \]$

(7)

단, $$ Z=\left[\begin{array}{cc}A& B\\ C& 0\end{array}\right]$$

[Step 6] 최적 게인을 이용하여 제어입력 u(t)를 구한다.

$\[ u\left(t\right)=-K_{1}x\left(t\right)+K_2{\int }_0^t{y}_e\left(t\right)dt+K_{1}x\left(0\right) \]$

(8)

상기 과정을 통하여 최적제어게인 K₁과 K₂는 다음과 같이 구해질 수 있다.

$\[ \begin{array}{c}{K}_1=\left[\begin{array}{ccc}\begin{array}{cc}59.0445& 0.1108\end{array}& \begin{array}{cc}0.0554& 6.4153\end{array}& \begin{array}{cc}3.7690& 1.8850\end{array}\end{array}\right]\hfill \\ K_2=1.7321\hfill \end{array} \]$

(9)

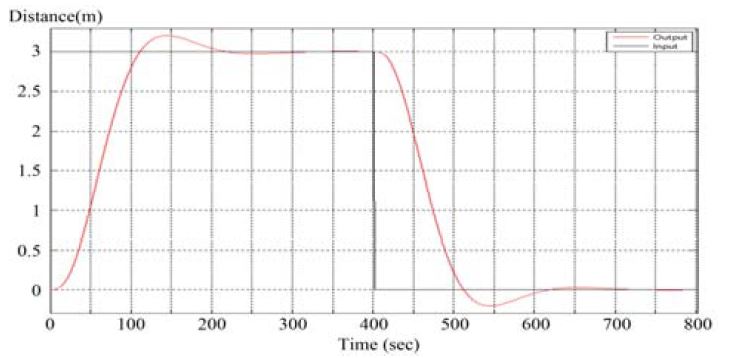
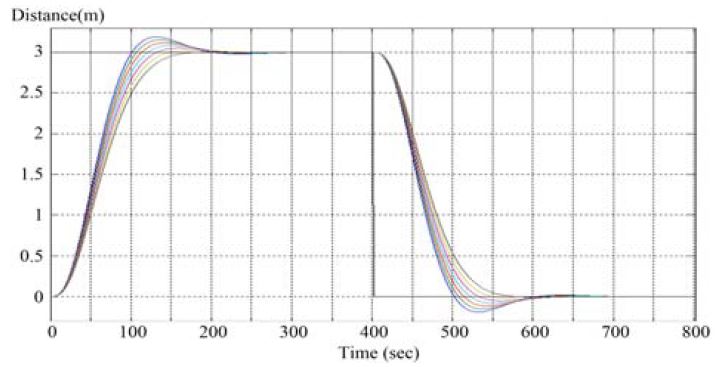
식 (9)와 같이 구해진 최적제어계인을 이용하여 강인서보제어기를 구성할 수 있으며, Matlab을 이용한[10][11] 시뮬레이션 결과는 Figure 3과 같이 나타낼 수 있다.

여기에서는 화물의 중량을 고려한 경우로서 오버슈트가 발생되고 있으나, 이는 하중계수 조절에 의해 개선될 수 있으며, 또한 반복제어계 설계를 통해서 개선될 수 있다.

Figure 3:

Step response of robust servo control system

3.2 반복 서보제어기 설계

임의의 주기의 목표신호를 추종하는 경우, 내부모델원리를 고려하여 일정한 주기를 가지는 주기신호를 내부에서 생성되도록 하는 기구가 만들어져야 한다. 이를 위해 일정주기마다 이전주기에서 생성된 제어입력과 새로운 에러 신호를 고려하여 새로운 제어입력을 생성할 수 있어야 한다.

이러한 주기함수 발생기를 반복보상기(Repetitive compensator)라고 하고 반복보상기를 이용하여 구성한 제어계를 반복제어계(Repetitive control system)라고 한다[7][12]-[14].

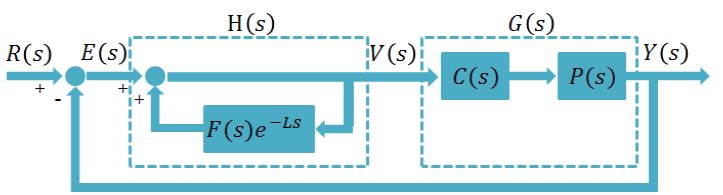
Figure 4는 반복제어계의 블록다이어그램을 나타낸 것으로 P (s ) 는 플랜트를 나타내며, C (s ) 는 제어기의 안정화를 위한 강인서보제어기, H (s ) 는 반복제어기, 그리고 F (s )는 반복제어기의 입력의 필터링을 위한 필터를 나타낸다. 본 연구의 반복제어계에서 반복보상기는 비례게인만 사용하였고 필터링은 고려하지 않았다.

Figure 4:

Repetitive Control system

반복제어계 시뮬레이션에서는, 첫 번째 루프에서는 초기에 설정된 값을 이용하여 계산을 하며, 초기값은 ‘0’으로 둘 수 있다. 각 루프에서 제어를 행할 때에는, 각 제어 샘플링 주기에 맞추어 전체 데이터 베이스를 구성하고, 이를 반복하여 한 루프 동안 시뮬레이션을 행하도록 한다.

첫 번째 사이클의 주행이 끝난 결과와 이때 전 샘플링 주기에 이용된 저장 Data(Input data, Output data and error data)를 통해 해당 주기의 입력 및 피드백 값을 조절하여 새로운 데이터를 생성하며, 이와 같은 흐름을 반복하여 전체 루프에서의 제어를 행하도록 한다.

반복제어계의 핵심 원리는 반복적으로 이전 주기의 정보 즉, 입력, 출력 및 오차 값들을 통해 현재의 제어입력을 결정하여 시스템으로 들어가는 신호를 조절하는 것이다. 이때 반복적으로 측정되어진 출력값의 최대치가 목표치와 가까운 출력이 나타나게 되면 오차가 거의 없는 것이 되어 반복제어는 완료가 되고 해당 제어계는 상태를 유지하여 일정한 출력을 나타내게 된다.

본 연구에서는 5회를 반복하는 반복제어계를 구성하여 시뮬레이션을 행하였으며, 시뮬레이션 결과는 Figure 5에서 확인할 수 있다. Figure 5에서 첫 번째 반복주기에 발생하였던 오버슈트는 반복제어계에 의해 5회 반복되는 중에 없어짐을 알 수 있다.

Figure 5:

Step response of Repetitive Control system

3.3 반복제어계를 이용한 동기화제어

본 연구에서의 동기화제어계를 구성하는 경우, 각 이동랙의 마스터 및 슬레이브를 정하고, 마스터의 주행경로를 목표입력으로 설정하여 슬레이브가 제어를 통하여 마스터의 주행경로에 동기화하도록 한다. 이를 위해 이동랙의 동기화제어에는 내부동기화 및 외부동기화로 구분되며, 내부동기화는 각 이동랙의 구동휠을 상호 동기화하는 부분이며, 외부동기화는 이동랙과 이동랙의 주행시의 동기화를 행하는 부분으로 한다.

3.3.1 동기화제어 방법

내부동기화시에 마스터와 슬레이브를 정할 때에, 적재화물이 많이 가해지는 부분의 구동부는 상대적으로 반응속도가 느리게 되므로, 이를 마스터로 하며, 나머지 부분은 슬레이브로서 지정하도록 한다. 즉, 이는 일정한 토크가 구동부에 주어져도 이동한 거리(구동휠 간의 동기화는 각 휠의 회전각도)가 작은 이동랙이 있다면 이는 적재 화물의 무게가 많이 나가거나, 기계의 내부적인 요소 그리고 주변 환경 등의 외부적인 요소로 인해 속도(구동휠 간의 동기화에서는 각 휠의 각속도)가 평균보다 낮아지기 때문에 이를 마스터로 지정하는 것이다.

내부동기화에서는 주행중인 구동휠 사이의 오차를 측정하여 동기화 반복제어계를 적용한다면, 제어를 적용하기 전보다는 주행 궤적과 구동부의 작동 결과 사이의 오차가 많이 줄어들 것이다. 하지만 이것만으로는 주행 궤적과 최종 작동 결과를 정확히 일치시켜 최종 목표에 달성하기는 어려움이 있다. 아무리 오차를 줄인다고 해도 줄여나가는 상황에서의 오차로 인해 조금은 차이가 남아 있는 것이다

외부동기화 제어방법에서는 4대의 이동랙을 가정하여 외부동기화 제어계를 구성하고자 한다. 이때 1대의 이동랙은 마스터가 되며, 나머지 3대는 슬레이브로서 구성될 수 있다.

3.3.2 동기화제어 알고리즘

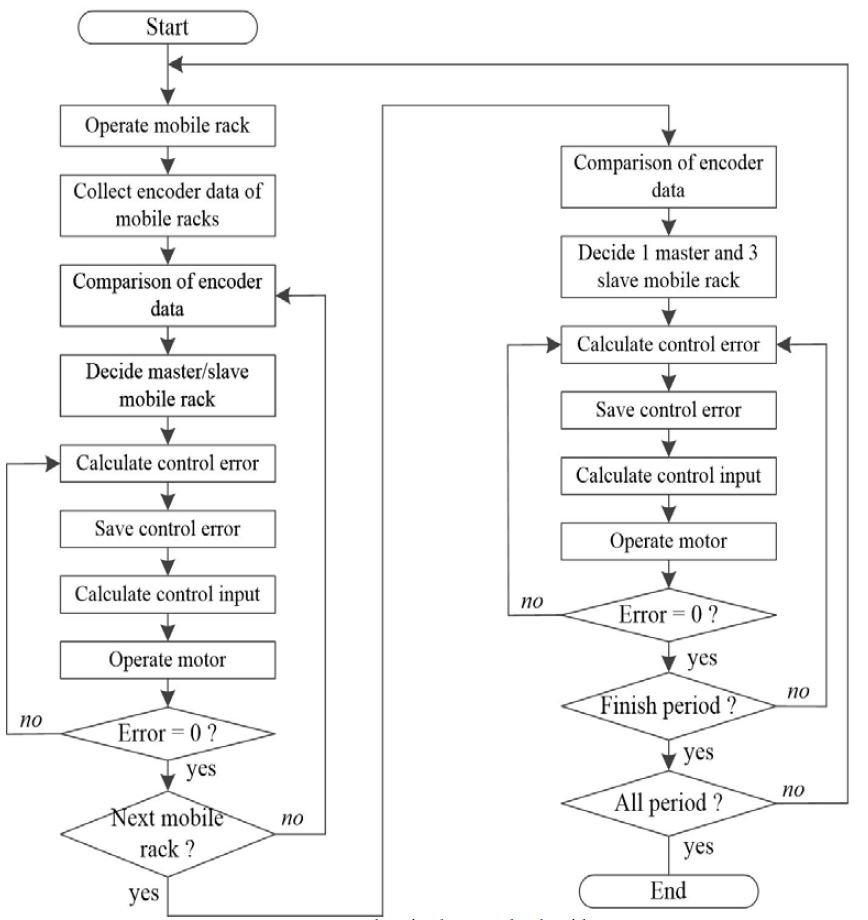
동기화제어 알고리즘에서는 Figure 6과 같이 내부동기화 및 외부동기화를 순차적으로 반복제어계를 구성하도록 한다. 이때, 화물의 하중분포를 고려하여 시나리오별로 구성하며, 각 시나리오별로 순차적으로 반복제어계를 구성하여 시뮬레이션을 행하며, 이때의 반복제어계의 파라미터를 저장하도록 한다.

Figure 6:

Synchronized Control Algorithm

3.3.3 동기화제어 시뮬레이션

상기 동기화 제어 알고리즘을 통하여, 단일 이동랙의 주행 결과가 정해진 주행 궤적을 추종할 수 있도록 제어하고자 한다. 시뮬레이션은 MATLAB을 이용하여 시뮬레이션을 행하며, 동기화 제어를 적용하기 전과 후로 나누어 실험결과를 비교하도록 한다.

Figure 7과 8은 동기화제어기를 이용하기 전과 후의 시뮬레이션 결과로서, 이동 목표치를 1[m]로서 내부동기화를 고려하여 시뮬레이션을 행한 MATLAB 결과이다. 이때 화물의 불균형을 고려하여 한쪽은 적재되는 화물의 파라미터 값을 임의로 조절하여서 좌우의 부하가 다르게 하여 시뮬레이션을 행하였다. 시뮬레이션 결과에서 알 수 있듯이 초기의 좌우측의 주행 편차가 있음을 알 수 있다.

Figure 7:

Control response of Repetitive Controller without Synchronized Control Algorithm

Figure 8:

Control response of Repetitive Controller with Synchronized Control Algorithm

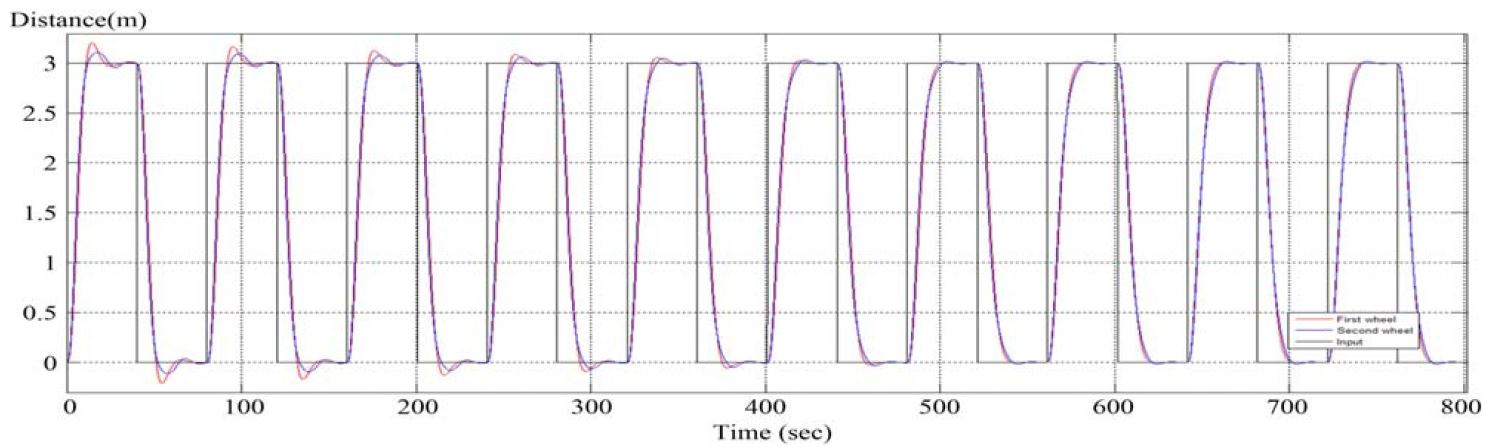
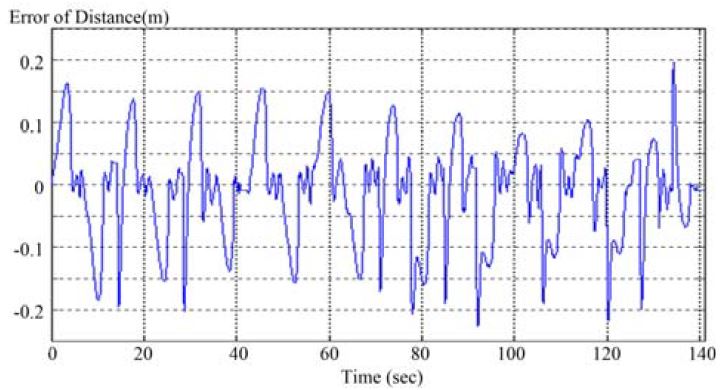
또한, Figure 9와 10은 동기화제어 전후의 결과로서, Figure 9결과에서는 주기를 반복할수록 목표값에 가까워지는 결과를 보이고 있으나, 이는 두 구동휠 사이의 오차가 많이 줄어든 것처럼 보일 뿐 중간 과정에는 여전히 오차가 존재하는 것을 알 수 있다.

Figure 9:

Control response of Repetitive Controller without Synchronized Control Algorithm

Figure 10:

Control response of Repetitive Controller with Synchronized Control Algorithm

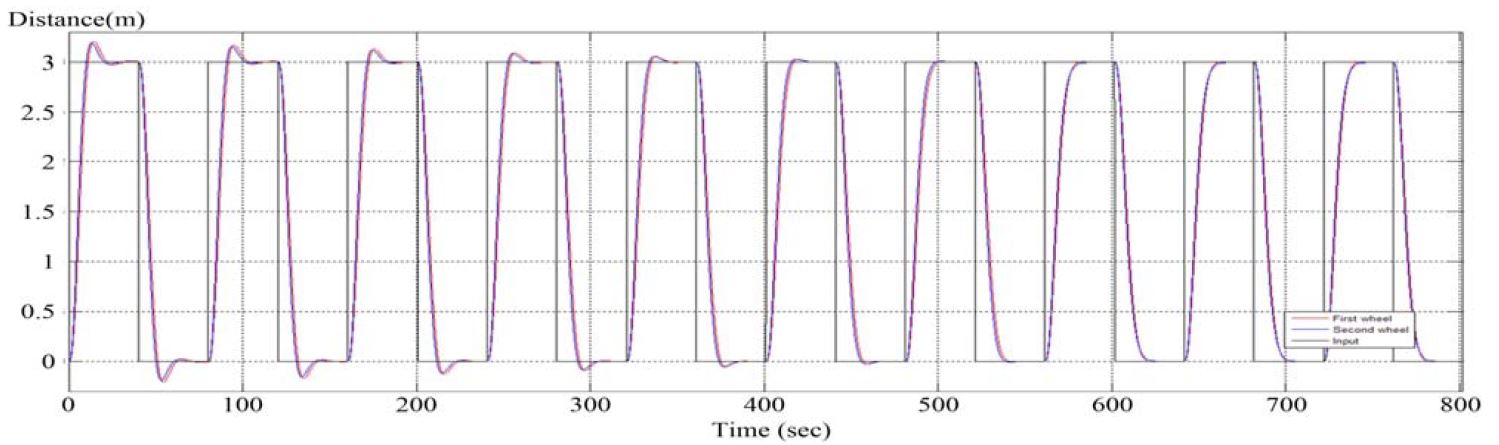
그러나 Figure 10에서는 내부동기화를 고려한 동기화제어계의 결과로서, 반복제어를 통해 각 주기내에서 목표값과 출력값 사이의 오차도 줄여가는 것을 확인할 수 있으며, 약 10회의 주기에서는 오버슈트도 없어지며 동기화 효과가 43%이상 향상됨을 볼 수 있다.

4. 동기화제어 실험 및 고찰

4.1 이동랙 실험장치 구성

본 연구에서는 전절에서 시뮬레이션으로 보여 진 제어알고리즘 효과를 실험으로서 입증하고자 한다. 이를 위해서 실제 이동랙의 1/8크기의 4개의 이동랙으로 2 × 2형태로 구성하여 Figure 11과 같이 2개 열에 각각 2개의 이동랙이 설치되었다.

이동랙 베이스 모듈은 구동부와 컨트롤 파트로 나뉘며, 전후, 좌우에 4개의 모터와 휠로 구성되고 있으며, 2단 적재랙으로 구성되고 있다.

Figure 11:

Experimentation equipments

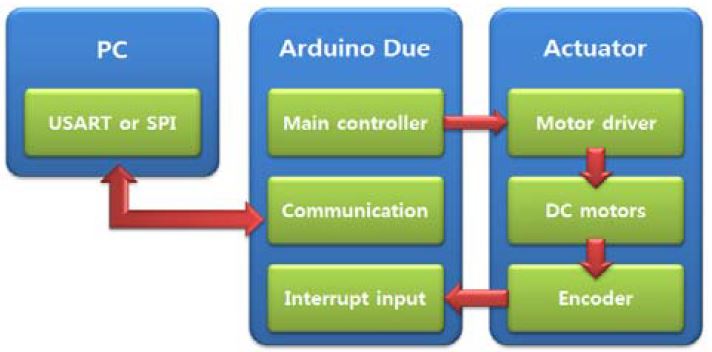
본 실험 장치는 Figure 12와 같이 PC, Arduino Due 및 Actuator로 구성되며, 각 이동랙에는 Actuator가 이동랙 구동을 담당하며, 각 이동랙의 제어를 위해 Arduino Due가 사용되었으며[15][16], 상위 프로그램으로서 PC를 이용하여 통제하도록 한다.

PC에서는 Arduino Due를 통제하여 각 이동랙 구동에 의한 엔코더 데이터 결과를 Xbee 통신에 의해 전송받는다. 또한, Arduino Due는 PC의 명령에 따라 이동랙에 제어 신호를 보내게 되는데 Analog Output을 통해 모터 작동 PWM을 출력하고 Digital Output을 통해 모터가 구동될 방향에 대한 정보를 출력하여 모터를 구동시킨다.

모터의 엔코더 데이터를 측정하기 위해서 Digital Input에 인터럽트을 적용하여 엔코더 펄스를 측정하도록 한다.

Figure 12:

System Configuration of Experimental model

4.2 이동랙 실험결과

본 실험에서는 이동랙의 무부하 상태에서 한쪽에만 약간의 하중을 인가한 상태로서 반복적으로 이동하도록 한다.

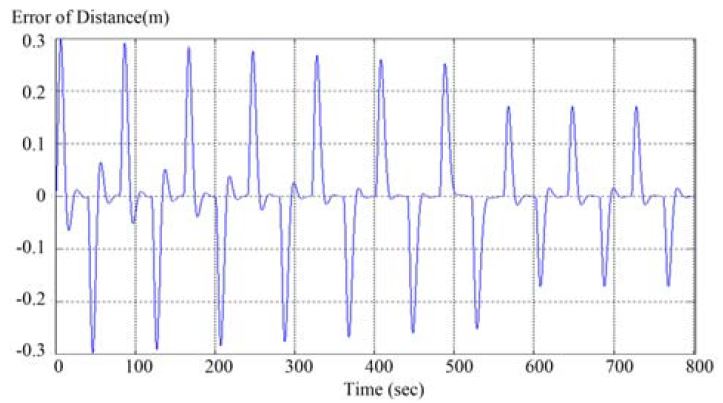
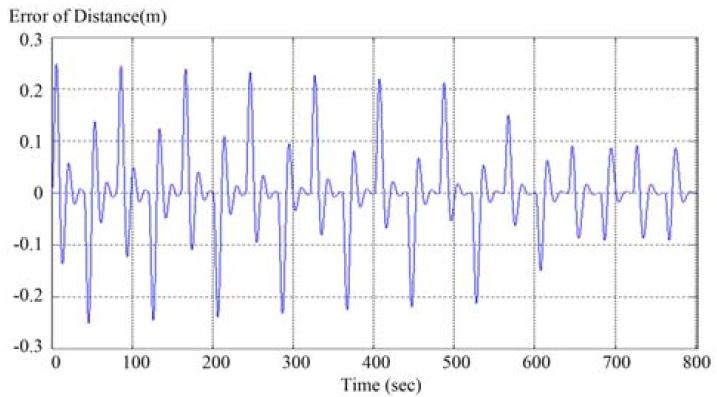
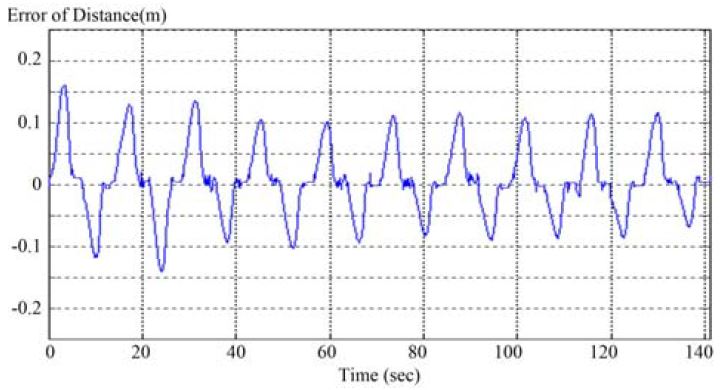
Figure 13와 14는 동기화제어를 행하기 전과 후의 주행모터의 엔코더의 동기화제어 오차 결과를 나타내고 있다.

Figure 13:

Control response of Repetitive Controller without Synchronized Control Algorithm

Figure 14:

Control response of Repetitive Controller with Synchronized Control Algorithm

동기화제어기를 행하지 않은 Figure 13 에서는 오차의 수렴정도가 불규칙하게 나타나며, 전진 및 후진시의 오차 편차가 크게 나타나는 것을 알 수 있다.

그러나 동기화제어기를 행한 Figure 14 에서는 초기의 오차가 Figure 13 과 유사하나, 반복을 행함으로서 점차 오차수렴이 진행되는 것을 알 수 있으며 특히 전진과 후진시의 오차 편차가 적음을 알 수 있다.

동기화제어기 초기 게인 설계시, 시스템의 관성 등과 관련이 있으므로 오차의 수렴정도를 고려하여 반복하면서 점차 적정 게인으로 조정할 필요가 있다.

5. 결 론

본 논문에서는 무궤도 이동랙에 대해 내부적동기화 및 외부적 동기화를 행하는 동기화알고리즘을 반복제어계를 바탕으로 제안하였다. 또한, 이때 반복제어계의 안정화제어기는 파라미터 변동에 강건한 강인서보제어계를 이용하여 설계하였다.

이동랙의 수학적 모델링을 이용하여 화물하중 변동에 강건한 강인서보 제어계, 이를 이용한 반복제어계 및 구동휠간의 반복 주행특성을 고려한 동기화제어계에 대하여 MATLAB을 이용하여 시뮬레이션을 행하여 그 유효성을 검증하였다. 또한, 검증된 시뮬레이션 결과를 통하여 실제 1/8 크기의 모형을 통하여 실험을 행하였으며, 실험결과에서도 ± 12[mm] 이내에 수렴함을 확인할 수 있었다.

그러나 본 연구에서 사용된 이동랙은 동력전달계 및 하부 프레임의 진동으로 인하여 실험오차가 크게 영향을 미쳤으며, 향후 이러한 동력전달계 및 플렉시블한 구조물의 특성을 고려한 모델 보완 및 이를 위한 제어계 설계기법 개발이 필요할 것으로 사료된다.

Acknowledgments

본 연구는 국토교통부 교통물류연구개발사업의 연구비지원(과제번호 15LRP-B079281-02)에 의해 수행된 연구결과이며, 박진의 석사학위논문(“반복제어계를 이용한 무궤도 이동랙 동기화제어계 설계, 한국해양대학교 대학원”)에 근거한 것이다.

References

• Ministry of Land, Infrastructure and Transport, “Multi-mobile rack technology for storage efficiency”, p441, (2016), (in Korean).
• A. S. Raymond, S. F. Jerry, and V. Chris, College Physics, (8th Edition), Cengage Learning, Books-Hill Publishers, (2011), (in Korean).
• H. S. Kim, and S. Kawaji, “Modelling and its characteristics for AS/RS stacker crane in high rack automated warehouse system”, Korean Society of Power Engineering, p369-374, (1999), (in Korean).
• H. S. Kim, and S. Kawaji, “Position control of AS/RS Stacker Crane by Using Gain-Scheduled Control Method in Automated High Rack Warehouse System”, Procedure of the 14th KACC, E, p198-201, (1999).
• K. Ogata, Modern Control Engineering, (4th edition), Cyber Media Publisher, (2003), (in Korean).
• S. B. Kim, and J. S. Ha, Basic Control Theory, Hanmi Publishers, (1990), (in Korean).
• I. K. Kim, T. K. Yeu, H. S. Kim, and S. B. Kim, “NOx reduction control for SCR system using repetitive control method in a refuse incineration plant”, Journal of Korean Society of Mechanical Engineering, 24(11), p2762-2770, (2000), (in Korean).
• M. O So, Y. H. Lee, S. J. Oh, K. G. Jin, and B. G. Jeong, “Synchronization of pehlivan chaos system using GA-based sliding mode control”, Journal of the Korean Society of Marine Engineering, 38(4), p424-429, (2014), (in Korean). [https://doi.org/10.5916/jkosme.2014.38.4.424]
• K. Furuta, S. Kawaji, B. Mita, and S. Hara, Mechanical Control, O-Mu Publishers, (1984), (in Japanese).
• S. Jung, Analysis of Control system and Application of Matlab and Simulink, ChungMunGak Publishers, (2010), (in Korean).
• W. J. Palm, Matlab 7 for Engineer, Kyobobooks Publisher, (2009), (in Korean).
• M. Nakano, M. Inoue, T. Yamamoto, and S. Hara, Repetitive control, Book Series of SCIE, (in Japanese).
• H. S. Kim, “AGC controller design by using repetitive control nethod”, The 2003 International Symposium on Mechatronics, p27-30, (2003).
• H. S. Kim, J. S. Park, S. D. Lee, K. J. Lee, and S. K. Park, “Repetitive compensation control for AGC system by using pre-pass rolling data”, Proceedings of International Conference on Control, Automation and Systems, p1040-1043, (2001).
• K. Y. Hye, Skech-up for Imagination of Aduino, J-Pup Publisher, (2014), (in Korean).
• M. Michael, and S. B. Yun, Learn of Aduino by Cookbook Recipe, J-Pup Publisher, (2014), (in Korean).