호버링 타입 자율무인잠수정 'OCTAGON'의 테스트베드 개발

1. 서 론

육상의 비재생 자원들의 고갈로 인해 인류는 많은 자원들이 존재하는 해양으로의 관심이 커지게 되었다. 하지만 접근성이 낮고 외란에 대한 불확실성이 큰 바다에서 인간이 작업하기는 쉽지 않았다. 따라서 무인잠수정을 활용하여 해양탐사 및 자원채취 등의 작업을 수행해 왔다.

이러한 무인잠수정은 크게 ROV(Remotely Operated Vehicle)와 AUV(Autonomous Underwater Vehicle)로 나눌 수 있으며, 그 중 AUV는 넓은 지역을 탐사하기 위한 항주형 타입 AUV와 특정 지역을 조사하고 수중에서의 작업을 수행하는 호버링 타입 AUV로 분류 할 수 있다[1]. 그 중 호버링 타입 AUV는 국부영역을 정밀 탐사하고 수중작업을 수행하기 위하여 자세제어 및 위치제어 기능이 매우 중요하다.

대표적인 호버링 타입 AUV로는 8개의 추진기를 장착하여 6자유도 운동을 제어할 수 있는 하와이대학교의 ‘ODIN’이 있다. ‘ODIN’은 수중항법을 위해 IMU(Inertial Measure Unit)를 사용하며 위치제어를 위한 센서로 소나를 사용한다[2]. 동경대학교에서도 호버링 타입 AUV의 연구를 활발하게 수행하고 있다. 1999년 정밀관측용 AUV인 ‘Tri-Dog 1’을 건조하였고, 6개의 추진기와 광학카메라를 이용하여 다양한 실해역 실험을 성공하였다[3]. 국내에서도 호버링 타입 AUV에 관한 연구가 활발히 진행되고 있으며, 대표적으로 제주대학교의 ‘NOAH’는 수중탐사용 호버링 타입 AUV의 Test-bed로써 4개의 추진기를 사용하여 4자유도 운동을 제어한다. 사용센서로는 압력계와 컴파스가 있으며 위치제어 및 항법을 위하여 SBL(Short Base Line) 위치측정시스템을 적용하기도 하였다[4][5].

본 연구의 최종 목표는 매니퓰레이터를 장착한 수중 작업용 호버링 타입 AUV의 개발이며, 본 논문에서는 이를 위한 기초 연구로써 호버링 타입 AUV의 test-bed를 제작하였다. 무인잠수정이 수중에서 작업 시 가장 중요한 기능은 조류외란 하에서 자세 및 위치를 유지하는 것이므로 본 논문 에서는 잠수정의 수심제어와 방향각 제어에 대한 연구를 수행하였다. 아래의 Figure 1은 실제 제작된 호버링 타입무인잠수정의 외형을 나타낸다.

본 논문의 2장에서는 개발된 호버링 타입 무인잠수정의 하드웨어 구성에 대해 기술하였고, 3장에서는 운동성능 확인을 위한 수학적 모델링과 위치 및 자세제어를 위한 제어기 설계과정을 설명하였다. 4장에서는 설계된 제어기의 성능 확인을 위한 시뮬레이션을 수행하였으며, 5장에서는 실제 무인잠수정의 제어성능을 확인하기 위해 실해역 성능실험을 수행하였고, 마지막 6장에서 결론을 언급하였다.

Figure 1:

Hovering-type AUV

2. 무인잠수정의 하드웨어 구성

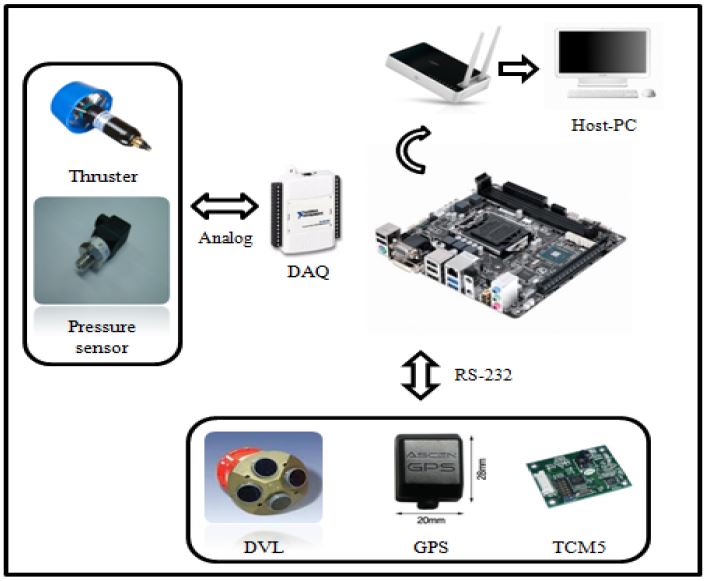
본 논문에서 설계된 무인잠수정은 호버링 타입 무인잠수정의 기초적인 운동성능 확인과 제어실험을 위한 Test-bed로서 무인잠수정의 수중항법시스템 또는 알고리듬 개발을 연구하기 위한 목적으로 Figure 2와 같이 시스템의 구성장치들이 설계 및 구성되었다. 제작된 무인잠수정의 제원은 Table 1과 같고, 다양한 계측센서 및 통신모듈 장착의 편리성을 위해 오픈 프레임 구조를 가지며 복원성 증가를 위해 상부에 부력재를 탑재하는 등 전통적인 방법을 사용하였다.

2.1 기구 시스템

제작된 무인잠수정의 외곽프레임은 스테인레스 스틸 재질을 사용한 8각형 형태이며, 프레임에 설치될 내압용기의 크기와 추진기의 크기를 고려하여 폭은 736mm, 높이는 600mm으로 설계하였고, 내부에 베터리 및 전장부를 적재하기 위해 알루미늄 6061 재질을 이용하여 외경 400mm, 내경 380mm, 높이 280mm의 내압용기를 설계하였다. 호버링 타입 무인잠수정은 다수의 추진기를 제어하여 원하는 운동을 수행하게 되는데, 본 연구에서는 수평추진기로 Tecnadyne사의 Model 300을 사용하였고, 수직추진기는 동일 회사의 Model 280을 사용하였다. 추진기의 입력전압은 24V이며 ±5V 아날로그 제어명령으로 전·후진 추력을 발생한다. 현재는 수평추진기 2대와 수직추진기 2대를 사용하고 있으며 추후 외란을 극복하는 추진력을 얻기 위해 수평추진기 4대와 수직추진기 4대를 장착할 계획이다.

Table 1:

Specifications of hovering-type AUV

2.2 계측 시스템

수중에서 무인잠수정의 위치와 자세를 제어하기 위해서는 무인잠수정의 상태 값을 측정하는 센서들이 필요하다. 따라서 본 연구에서는 수심을 측정할 수 있는 압력센서, 위치와 속도 측정을 위한 GPS 및 DVL(Doppler Velocity Log), 그리고 방향각을 측정하는 TCM-3 센서를 사용하였다. 또한 압력센서의 디지털 측정값을 얻고 추진기의 제어신호 입출력을 위해 DAQ 보드를 이용하였다. Figure 2는 전체 시스템 구성에 대한 블록다이어그램을 나타낸다.

제작된 호버링 타입 무인잠수정은 육상의 호스트 PC로부터 무선으로 명령을 전송받고 이후 무인잠수정은 제어기에 의해서 명령을 수행하게 된다. 전원은 25.7V-6.6Ah 리튬 폴리머 베터리 6팩을 사용하였으며 3시간 구동이 가능하도록 설계되었다.

Figure 2:

System configuration

3. 무인잠수정의 수학적 모델 및 제어기 설계

무인잠수정은 운용자에 의해 조종되는 것이 아니고 주어진 명령에 따라 스스로 원하는 자세를 유지하고 목표 위치에 도달하여야 하며, 주위환경의 변화를 감지하여 주행경로를 판단하는 잠수정이므로 제어시스템이 필수적이다. 이런 제어시스템을 개발하기 위해서는 여러 번의 설계와 실험을 반복해야 하고 적지 않은 인력과 시간이 소모된다. 따라서 무인잠수정을 설계하기 위해서는 우선 무인잠수정의 운동을 수학적 모델을 이용하여 운동성능이나 제어성능을 해석하는 과정이 필요하다. 따라서 본 논문에서는 무인잠수정의 운동 상태를 해석할 수 있도록 6자유도 비선형운동 방정식을 유도하고, 이 운동방정식을 이용하여 다양한 입력과 환경 하에서 무인잠수정의 운동성능을 확인하였다.

3.1 좌표계 설정 및 무인잠수정의 수학적 모델

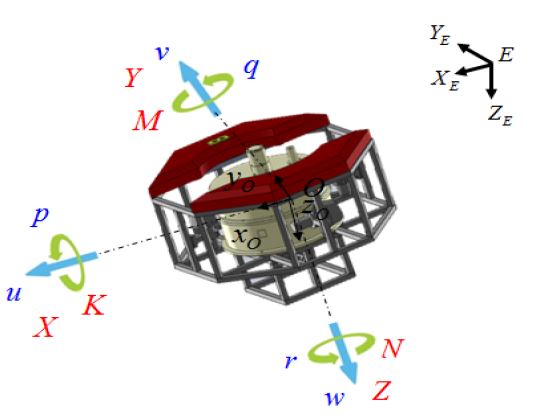
무인잠수정의 운동방정식을 유도하기 위해서 무인잠수정을 강체라 가정하고 Figure 3과 같이 지구고정좌표계(Earth-fixed coordinates)와 무인잠수정의 질량중심에 선체고정좌표계(Body-fixed coordinates)를 설정하였다. 설정된 좌표계는 선수방향을 x_o축, 우현방향을 y_o축 그리고 수직방향을 z_o으로 하는 오른손 좌표계를 사용하였다.

Figure 3:

Coordinate system

또한 설정된 선체고정좌표계의 각 축에 대한 병진운동과 회전운동을 6자유도 방정식으로 표현할 수 있고, 이를 식 (1), 식 (2)에 표현하였다[6]. 이때 사용된 표기법은 Table 2와 같다.

식 (1)의 좌변은 무인잠수정의 질량(m), 무게중심(x_g,y_g,z_g ), 질량관성 모멘트(I), 및 선체고정좌표계에서 표현되는 무인잠수정의 선속도(u,v,w) 및 각속도(p,q,r)를 나타낸다. 식 (2)는 무인잠수정에 작용하는 외력을 나타내는 항으로 부가질량에 의한 힘, 코리올리 힘, 복원력, 추진기에 의한 힘 등이 포함된다. 식 (2)에 포함된 X_u|u|,Y_v|v|,Z_w|w|와 같은 유체력 계수는 실험 또는 경험식에 의해 구할 수 있다. 본 연구에서는 기존에 발표된 유사선형의 유체력 계수를 사용하였으며 Table 3과 같다[7].

$\[ \begin{array}{c}\begin{array}{c}m\left[\dot{u}-vr+wq-x_g\left(q^2+r^2\right)+y_g\left(pq-\dot{r}\right)+z_g\left(pr+\dot{q}\right)\right.=\sum X_{ext}\hfill \\ m\left[\dot{v}-wp+ur-y_g\left(r^2+p^2\right)+z_g\left(qr-\dot{p}\right)+x_g\left(qp+\dot{r}\right)\right.=\sum Y_{ext}\hfill \\ m\left[\dot{w}-uq+vp-z_g\left(p^2+q^2\right)\right.+x_g\left(rp-\dot{q}\right)+y_g\left(rq-\dot{p}\right)=\sum Z_{ext}\hfill \end{array}\hfill \\ \begin{array}{c}{I}_{xx}\dot{p}+\left(I_{zz}-I_{yy}\right)qr-\left(\dot{r}+pq\right)I_{xz}+\left(r^2-q^2\right)I_{yz}+\left(pr-\dot{q}\right)I_{xy}+m\left[y_g\left(\dot{w}-uq+vp\right)-z_g\left(\dot{v}-wp+ur\right)\right]=\sum K_{ext}\hfill \\ I_{yy}\dot{q}+\left(I_{xx}-I_{zz}\right)rp-\left(\dot{p}+qr\right)I_{xy}+\left(p^2-r^2\right)I_{xz}+\left(qp-\dot{r}\right)I_{yz}+m\left[z_g\left(\dot{u}-vr+wq\right)-x_g\left(\dot{w}-uq+vp\right)\right]=\sum M_{ext}\hfill \\ I_{zz}\dot{r}+\left(I_{yy}-I_{xx}\right)pq-\left(\dot{q}+rp\right)I_{yz}+\left(q^2-p^2\right)I_{xy}+\left(rq-\dot{p}\right)I_{xz}+m\left[x_g\left(\dot{v}-wp+ur\right)-y_g\left(\dot{u}-vr+wq\right)\right]=\sum N_{ext}\hfill \end{array}\hfill \end{array} \]$

(1)

$\[ \begin{array}{c}\begin{array}{c}\sum X_{ext}=X_{HS}+X_{u}u+X_{u\left|u\right|}u\left|u\right|+X_{\dot{u}}ur-X_{\dot{u}}uq+X_{\dot{u}}uw-X_{\dot{u}}uv+\sum F_x\hfill \\ \sum Y_{ext}=Y_{HS}+Y_{v}v+X_{v\left|v\right|}v\left|v\right|+Y_{\dot{v}}vp-Y_{\dot{v}}vw+Y_{v}uv-Y_{v}vr+\sum F_y\hfill \\ \sum Z_{ext}=Z_{HS}+Z_{w}w+Z_{w\left|w\right|}w\left|w\right|+Z_{\dot{w}}wq-Z_{\dot{w}}wp+Z_{\dot{w}}vw-Z_{\dot{w}}uw+\sum F_z\hfill \end{array}\hfill \\ \begin{array}{c}\sum K_{ext}=K_{HS}+K_{p}p+K_{p\left|p\right|}p\left|p\right|+K_{\dot{p}}pr-K_{\dot{p}}pq+\sum M_x\hfill \\ \sum M_{ext}=M_{HS}+M_{q}q+M_{q\left|q\right|}q\left|q\right|+M_{\dot{q}}pq-M_{\dot{r}}qr+\sum M_y\hfill \\ \sum N_{ext}=N_{HS}+N_{r}r+N_{r\left|r\right|}r\left|r\right|+N_{\dot{r}}qr-N_{\dot{r}}pr+\sum M_z\hfill \end{array}\hfill \end{array} \]$

(2)

Table 2:

Notations of each axis

Table 3:

Parameters of hydrodynamic coefficients

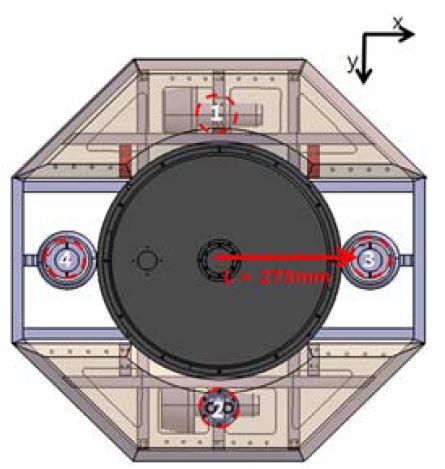
본 연구에서 제작된 호버링 타입 무인잠수정은 수직추진기와 수평추진기를 각각 2대씩 사용함으로써 4자유도의 운동(Surge, Heave, Pitch, Yaw)을 할 수 있게 된다. 따라서 각 추진기의 위치 및 방향을 고려하여 추진기의 힘과 모멘트를 무인잠수정의 운동방정식의 외력 항에 추가 할 수 있다. 추진기의 위치와 방향은 Figure 4에 나타나 있으며, 표시된 숫자 1, 2는 수평방향의 추진기를 나타내고 3, 4는 수직방향의 추진기를 나타낸다. 이때 각 축에 대한 힘과 모멘트는 식 (3)과 같다.

Figure 4:

Thrust configuration

$\[ \begin{array}{c}\begin{array}{c}\sum F_x=F_1+F_2\hfill \\ \sum F_y=0\hfill \\ \sum F_z=F_3+F_4\hfill \end{array}\hfill \\ \begin{array}{c}\sum M_x=0\hfill \\ \sum M_y=-l\bullet F_3+l\bullet F_4\hfill \\ \sum M_z=-l\bullet F_1+l\bullet F_2\hfill \end{array}\hfill \end{array} \]$

(3)

여기서 F _i 는 i번째 추진기의 추력, l 은 무인잠수정의 질량중심으로부터 추진기까지의 거리이다.

3.2 제어기 설계

본 연구에서는 무인잠수정의 위치와 자세를 제어하기 위해 PID 제어기 및 Fuzzy PID 제어기를 사용하였다. 또한 다수의 추진기를 사용하는 호버링 타입 무인잠수정에 적절한 추력을 분배하기 위한 추진기 구성행렬을 적용하였다[8][9].

앞절에 설명한 추진기의 위치와 방향을 고려한 각 축에 대한 힘과 모멘트는 식(4), 식 (5)와 같이 추진기 구성행렬 T를 이용하여 표현할 수 있다.

$\[ {\tau }_T={TF}_T \]$

(4)

$\[ T=\left(\begin{array}{cc}\begin{array}{cc}1& 1\\ 0& 0\end{array}& \begin{array}{cc}0& 0\\ 1& 1\end{array}\\ \begin{array}{cc}0& 0\\ l& -l\end{array}& \begin{array}{cc}-l& l\\ 0& 0\end{array}\end{array}\right) \]$

(5)

여기서 $$ {\tau }_T=\left[\sum F_x, \sum F_y,\sum F_z,\sum M_x,\sum M_y,\sum M_z\right]\text{'}$$를 나타내며, $$ F_T=\left[F_1, F_2,F_3, F_4 \right]\text{'}$$를 나타낸다. 위의 식을 이용하여 무인잠수정의 제어를 위한 추력 F_T 는 식 (6)과 같이 결정 할 수 있다.

$\[ F_T=T^{-1}\bullet {\tau }_T \]$

(6)

3.2.1 PID 제어기 설계

무인잠수정의 임의의 자세와 위치를 유지하기 위해 필요한 각 축의 힘과 모멘트를 계산할 필요가 있고, 이 힘과 모멘트를 결정하기 위해 PID 제어기를 설계하였다. 본 연구에서 개발된 무인잠수정은 앞서 설명한 바와 같이 4자유도운동을 제어할 수 있으므로 제어기에서 출력되는 제어입력은 x,z방향의 힘과 y,z방향의 모멘트가 된다.

설계된 수심제어기는 PD 제어기로 수심방향의 운동을 지배적으로 나타내는 변수인 수심과 피치방향의 운동을 고려하여 설계하였다. 설계된 수심제어기는 다음과 같은 식 (7)으로 표현 된다.

$\[ {\tau }_n=K_{pn}{e}_n+K_{dn}\dot{e_n} \]$

(7)

여기서 $$ \left\{\begin{array}{c}n=1 \text{일때} Heave \text{제어기,} e_1=Z_d-Z\\ n=2 \text{일때 }Pitch \text{제어기, }{e}_2={\theta }_d-\theta \end{array}\right.$$

Z_d 는 목표수심, Z 는 현재수심, θ_d는 목표피치각, θ 는 현재 피치각, K_p는 proportional gain, K_d는 derivate gain을 나타낸다.

또한, 무인잠수정의 선수각 및 직진속도를 제어하기 위해 설계된 PID 제어기는 식 (8)으로 표현된다.

$\[ {\tau }_n=K_{pn}{e}_n+K_{in}\int e_{n}dt+K_{dn}\dot{e_n} \]$

(8)

여기서 $$ \left\{\begin{array}{c}n=1 \text{일때} Yaw \text{제어기,} e_1={\psi }_d-\psi \\ n=2 \text{일때 }Surge \text{제어기, }{e}_2=u_d-u\end{array}\right.$$

ψ_d 는 목표방향각, ψ는 현재방향각, u_d는 목표속도, u는 현재속도, K _i 는 integral gain을 나타낸다.

본 연구의 PID 제어기에 사용된 이득 값은 시행착오 방법을 통하여 선정하였다.

3.2.2 Fuzzy PID 제어기 설계

퍼지 제어는 퍼지 추론 규칙에 의해 제어기의 성능이 결정되며, 계산 시간이 많이 걸리는 단점이 있지만 비선형적이고 복잡한 동적 특성의 변화를 지닌 시스템에 적용될 수 있으며, 따라서 기존의 PID 제어기보다 강인한 특성이 있는 제어기라 할 수 있다. 퍼지 제어방식은 여러 가지 방법으로 나눌 수 있으나, 본 연구에서는 퍼지 논리를 이용하여 설계된 PID 제어기의 이득값을 결정하도록 두 알고리즘을 조합하는 방법을 적용하였다. 일반적으로 퍼지 제어기는 퍼지화(Fuzzification), 퍼지규칙(Fuzzy Rule Base), 퍼지 추론(Fuzzy Inference) 및 비퍼지화(Defuzzification) 단계로 구성된다. 퍼지화는 일반적인 물리량을 퍼지 집합으로 표현해 주는 과정이며 이 과정에서 각 집합의 원소들의 소속정도를 계산해주는 함수를 소속함수(Membership Function)라 한다. 본 연구에서는 제어 대상에 따라 입력변수와 출력변수들의 소속함수를 설정하고 Table 4 와 5와 같이 퍼지규칙을 설정하였다. 각각의 퍼지규칙은 수심방향의 제어와 무인잠수정의 선수각 제어를 하기 위한 퍼지규칙을 나타내며, 출력값은 PID 제어기의 이득값이 된다. 퍼지규칙은 제어대상의 목표값과 현재값의 차이와 그 차이값의 시간에 따른 변화률을 고려하여 결정할 수 있도록 설정하였다. 여기서 NB(Negative Big), NS(Negative Small), PS(Positive Small), PB(Positive Big), N(Negative), S(Small), P(Positive), Z(Zero)는 멤버를 나타낸다.

Table 4 와 5는 결정된 제어규칙을 나타내며 본 논문에서는 수심방향 및 수직방향의 제어를 위한 PID 제어기의 제어이득(K_p)를 구하는 제어규칙만 나타내었다. 피치각도 및 속도제어 또한 위와 같이 제어규칙을 설정하여 각각의 제어이득을 구할 수 있도록 하였다. 또한 설정된 제어규칙은 Mamdani 방법을 통해서 추론하도록 하였으며, 비퍼지화 방법으로는 중심평균법을 사용하였다. 따라서 비퍼지화된 출력은 식(9)와 같이 정의된다.

$\[ dU=\frac{\sum _{i=0}^n{\mu }_{output}\left(w_i\right)\times w_i}{\sum _{i=0}^n{\mu }_{output}\left(w_i\right)} \]$

(9)

Table 4:

Fuzzy rules – gain Kp of depth control

Table 5:

Fuzzy rules – gain Kp of heading control

4. 제어성능 시뮬레이션 결과

수조에서의 실험이나 실해역 실험 이전에 다양한 조건에서 설계된 제어기의 성능을 확인하는 작업이 필요하다. 따라서 3장에서 전개된 운동방정식과 설계된 제어기를 이용하여 제어성능에 대한 시뮬레이션을 수행하였다. 본 연구에서는 Matlab/Simulink를 이용하여 수치 시뮬레이션 프로그램을 구성하였다.

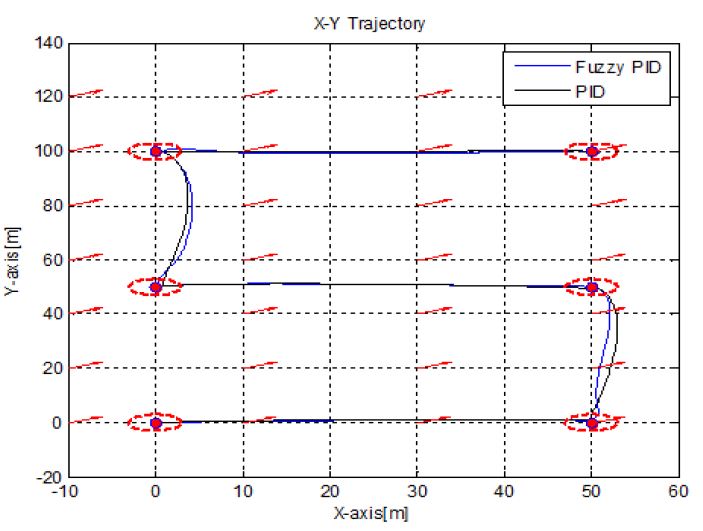
설계된 무인잠수정의 운동성능 및 제어기 성능을 확인하기 위하여 다음과 같이 시뮬레이션을 수행하였다. 호버링타입 무인잠수정은 일정지역을 탐사하기 위해서 주어진 경유점을 통과하여 목표점까지 도달해야 할 필요성이 있기 때문에 LOS(Line Of Sight)방법을 이용하여 목표 방향각을 결정하도록 하였고, 또한 설계된 PID 및 Fuzzy PID 제어기성능을 확인하는 시뮬레이션을 수행하였다. 또한 무인잠수정의 외란으로서 조류에 대한 모델을 2차원의 방향과 속도를 가지는 벡터로 가정하였고, 조류의 방향은 20°이며 속도는 0.1m/s로 설정하였다. 초기위치(0,0,0)에서 출발하여 수심 1m 아래로 잠항한 후, 미리 주어진 5개의 경유점(50,0,1), (50,50,1), (0,50,1), (0,100,1), (50,100,1)을 수심 1m를 유지한 채로 통과하여 최종위치 (50,100,0)에 도달하도록 시뮬레이션을 수행하였다.

Figure 5는 X-Y평면에서의 무인잠수정의 이동경로를 나타낸다. 그래프에서 나타난 각 격자점의 화살표는 조류 방향을 의미한다. 각 목표점을 통과하여 다음 목표점으로 방향각이 전환 될 때 무인잠수정은 조류에 의해 밀려나는 것을 볼 수 있으나 두가지 제어기 모두 주어진 목표점을 잘 찾아가는 것을 확인 할 수 있다.

Figure 5:

X-Y trajectory

Figure 6은 3차원의 무인잠수정 이동 경로를 나타내며, 초기위치 (0,0,0)에서 수심방향으로 1m 잠항 후 다음 목표점의 방향각을 찾고 이동하는 것을 확인 할 수 있다. 또한 5번째 목표지점에 도달한 후 다시 수평면으로 부상하는 것을 확인 할 수 있다.

Figure 6:

3D trajectory

Figure 7에서는 무인잠수정이 초기에 목표수심 1m에 잠항하고 수심을 유지하면서 이동하는 것을 확인 할 수 있으며, 마지막 경유점에 도달한 후 다시 수면으로 부상하는 것을 확인 할 수 있다.

Figure 7:

Result of depth control

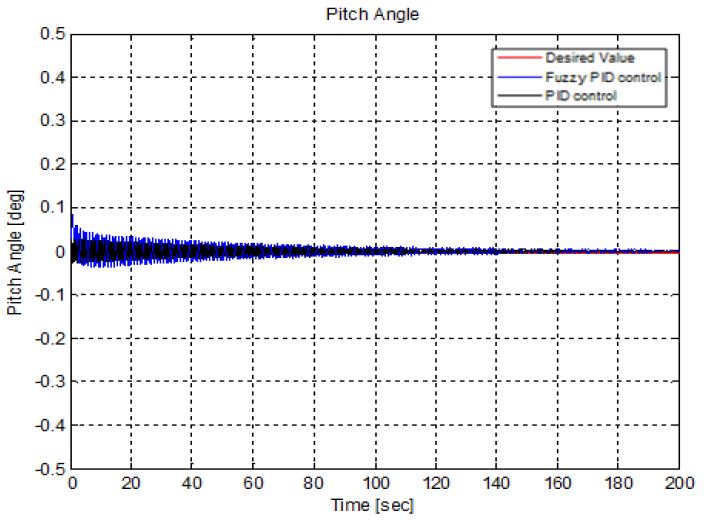
Figure 8은 무인잠수정의 피치각을 제어한 결과 그래프를 나타낸다. 무인잠수정의 운동에서 수심방향의 운동과 y축의 회전은 서로 영향을 미치기 때문에 피치각 또한 제어할 필요성이 있고, 본 논문에서는 호버링 타입 무인잠수정의 특성을 고려하여 수심방향의 운동 시 발생하는 피치각은 0°로 설정하였다. Figure 8에 나타나듯이 초기에 약 0.05° 내에서 진동이 있는 것을 확인 할 수 있으며 시간이 지남에 따라 0°에 수렴하는 것을 알 수 있다.

Figure 8:

Result of pitch angle control

Figure 9는 주어진 목표점을 찾아가는 동안 무인잠수정의 방향각을 나타내고, 이때 무인잠수정의 목표 방향각은 LOS 방법을 이용하여 결정하게 된다. 시뮬레이션 결과는 PID 제어기 및 Fuzzy PID 제어기 모두 유사한 제어성능을 보이고 있음을 알 수 있다.

시뮬레이션 결과 두 가지 제어기로 조류외란 하에서 경유점 제어가 어느 정도 잘 이루어짐을 볼 수 있었고 가능성을 확인하였다. 그러나 모델링 오차 및 유체력 계수의 값이 실제와는 다르므로 실해역 실험을 통하여 제어성능을 살펴보는 것이 필요하다.

Figure 9:

Result of heading angle control

5. 실해역 성능 실험

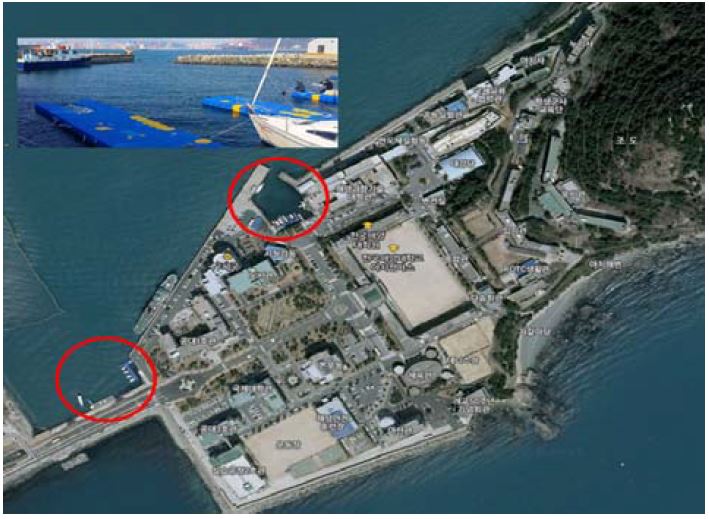
본 연구에서 설계 및 제작된 호버링 타입 무인잠수정의 운동성능 확인과 제어기 성능 확인을 위해 Figure 10에서 보이는 한국해양대학교에 위치한 요트계류장에서 실해역실험을 수행하였다. 본 논문에서 수행한 실해역 실험의 최종 목표는 일정한 수심을 유지하면서 주어진 목표점을 지나 시작점으로 돌아오는 경유점 제어이다. 경유점 제어는 PID 제어기와 앞 장에서 설계된 Fuzzy PID 제어기를 적용하여 실험을 수행하였다. 운항경로 계획을 위하여 기본적인 LOS 방법을 이용하였으며, DVL 센서를 이용하여 잠수정의 위치를 계산하고 TCM-3를 이용하여 방향각을 측정하여 제어를 수행하였다.

Figure 10:

Field test site

5.1 PID 제어기

5.1.1 수심 제어

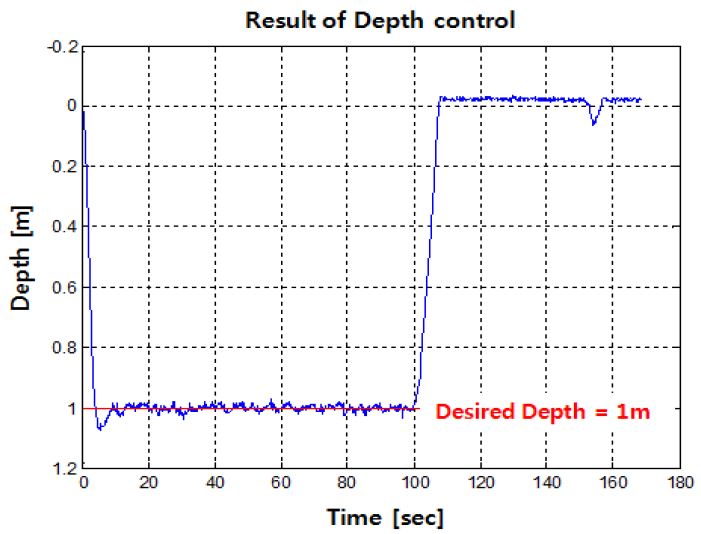
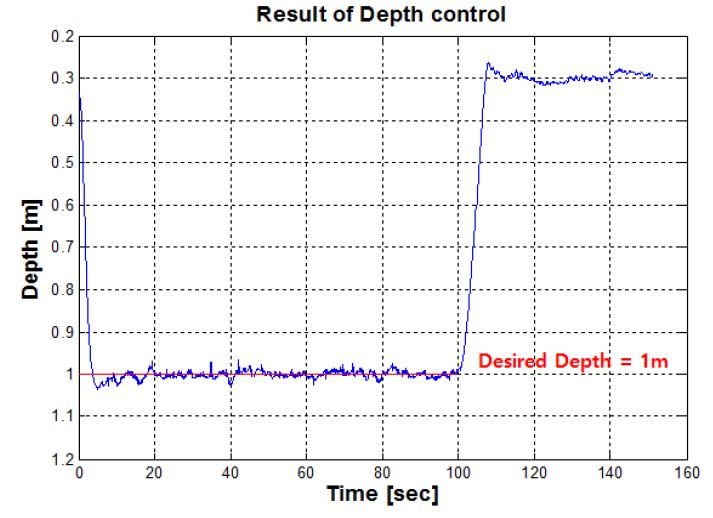
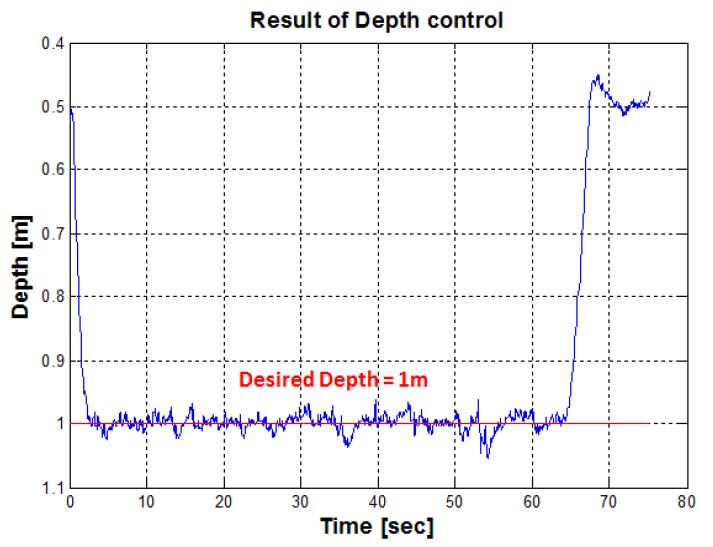
무인잠수정이 목표수심을 잘 추종하는지에 대한 제어성능을 확인하기 위해 수심제어를 실시하였으며 Figure 11은 수심제어를 수행한 결과 그래프를 나타낸다. 목표수심은 1m로 설정하였으며 100초 이후 수면으로 부상하는 무인잠수정의 수심방향 궤적을 확인 할 수 있다. 제어명령 초기에 무인잠수정이 수심방향의 운동을 하면서 관성에 의해 오버슈트가 발생하는 것을 확인 할 수 있고, 약 10초 이후 정상상태에 도달하는 것을 확인 할 수 있다. 수심 값이 진동을 보이는 것은 무인잠수정에 작용하는 외란 또는 추진기의 입력 값의 변화에 따른 현상이라고 할 수 있다. 하지만 그 크기가 크지 않고 목표수심을 잘 추종하는 것을 확인 할 수 있다.

Figure 11:

Result of depth control

5.1.2 방향각 제어

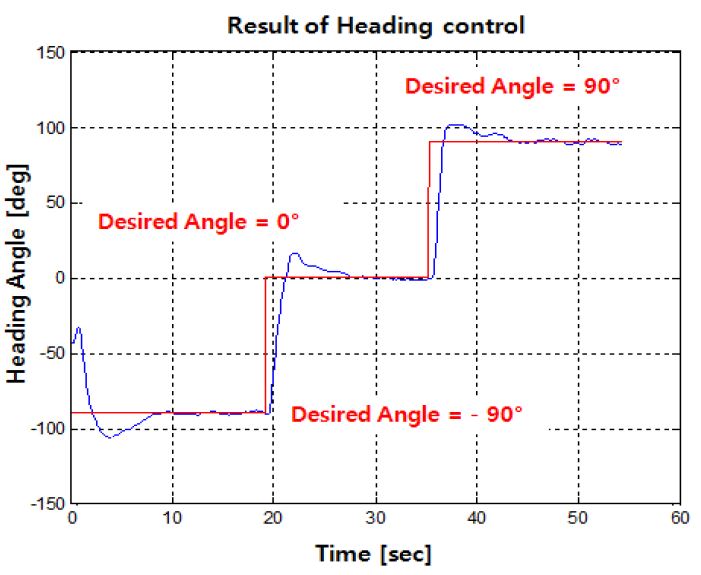
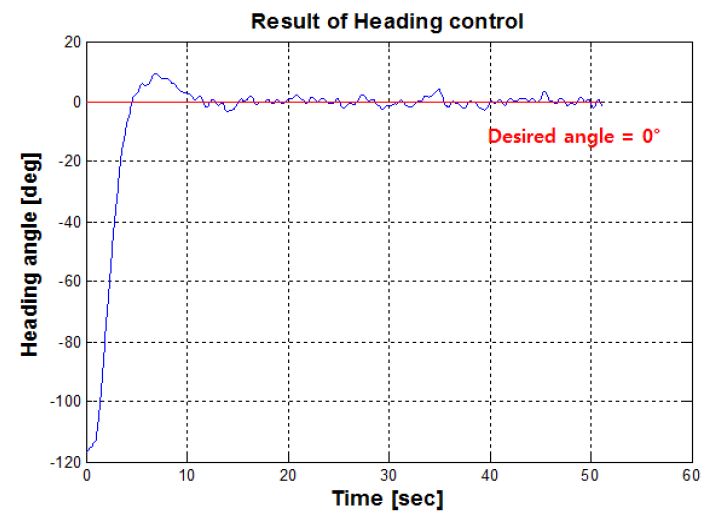
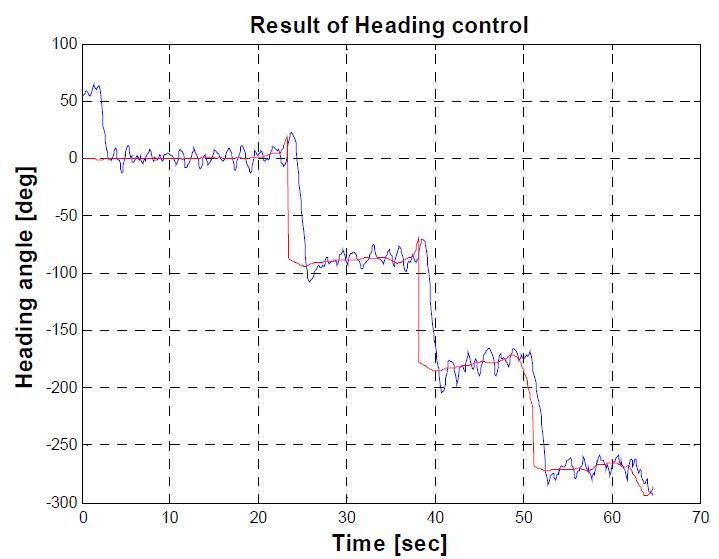
목표 경유점을 찾아가기 위해서는 방향각에 대한 제어성능을 확인하여야 하므로 방향각 제어를 실시하였으며 Figure 12는 방향각 제어에 대한 결과 그래프를 나타낸다. 초기 무인잠수정의 방향각은 –50°를 나타내고 있고, 이후 첫 번째 목표 방향각인 –90°에 수렴하는 것을 알 수 있다. 약 20초 및 35초 후 목표 방향각을 0°와 90°로 설정하였으며 약간의 오버슈트를 가지고 이후 목표값에 도달하는 것을 알 수 있다.

Figure 12:

Result of heading control

5.1.3 경유점 제어

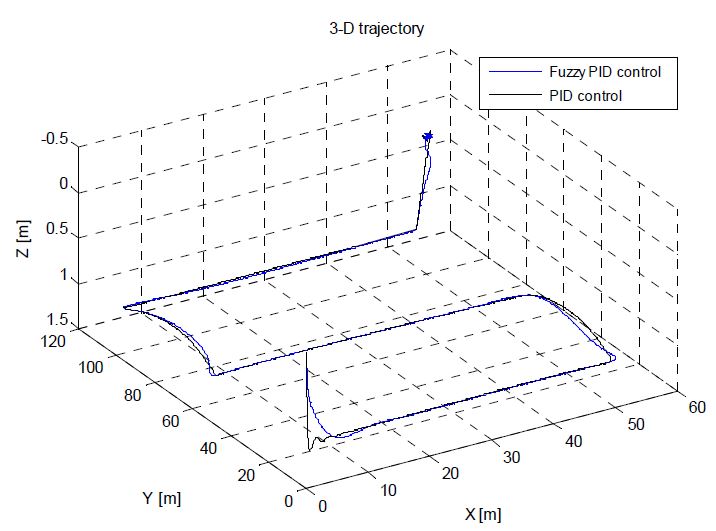
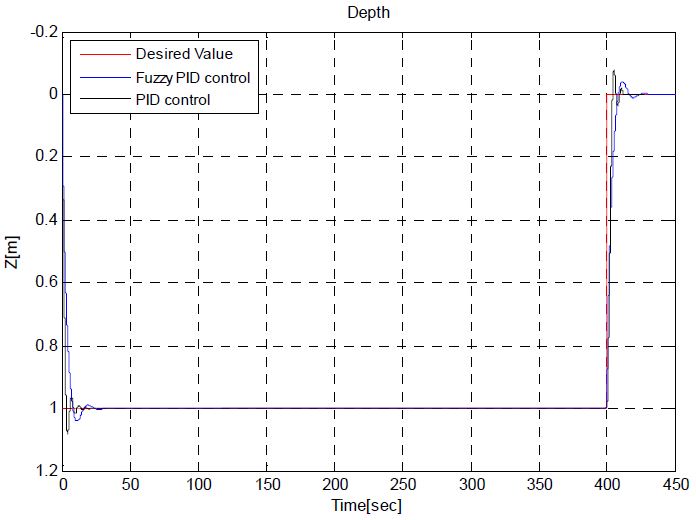
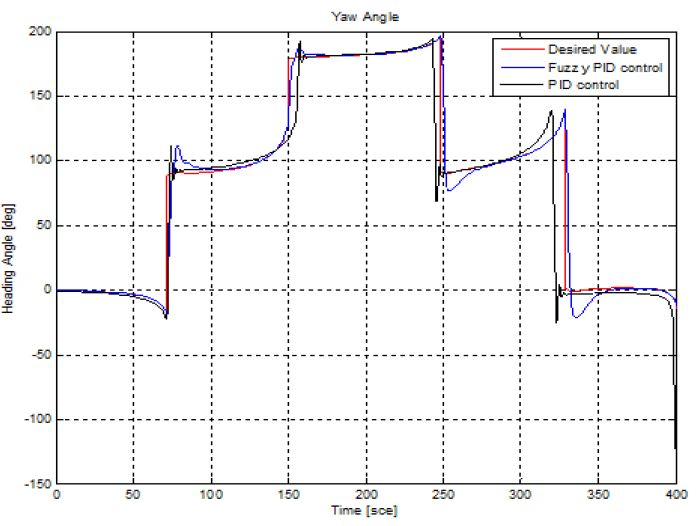
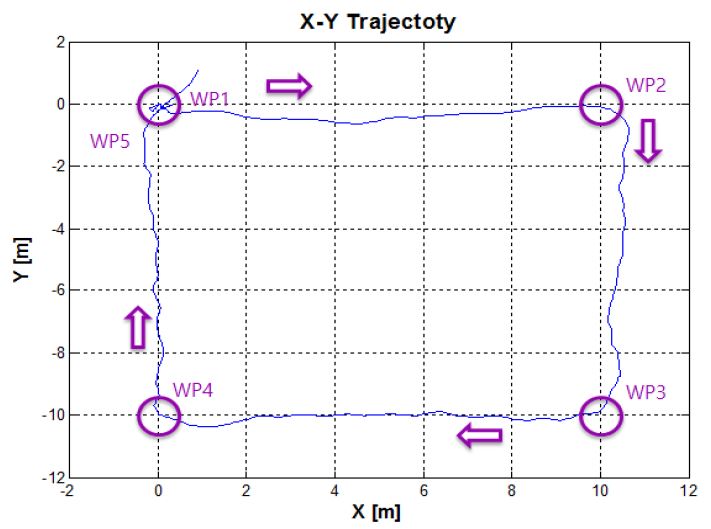
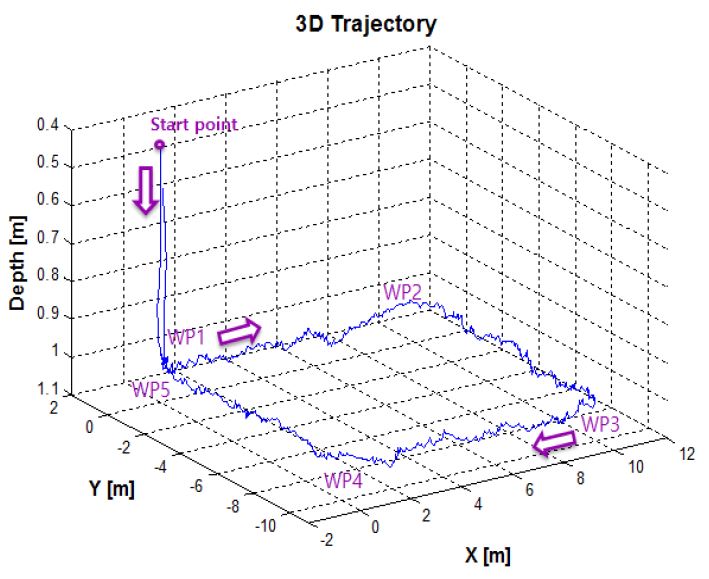
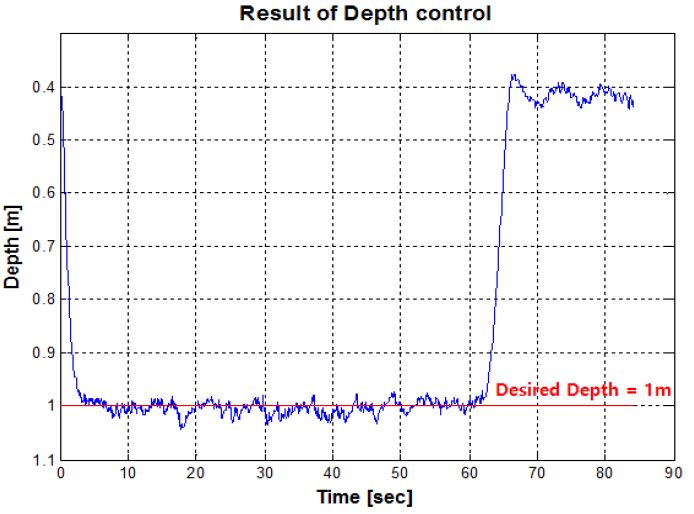
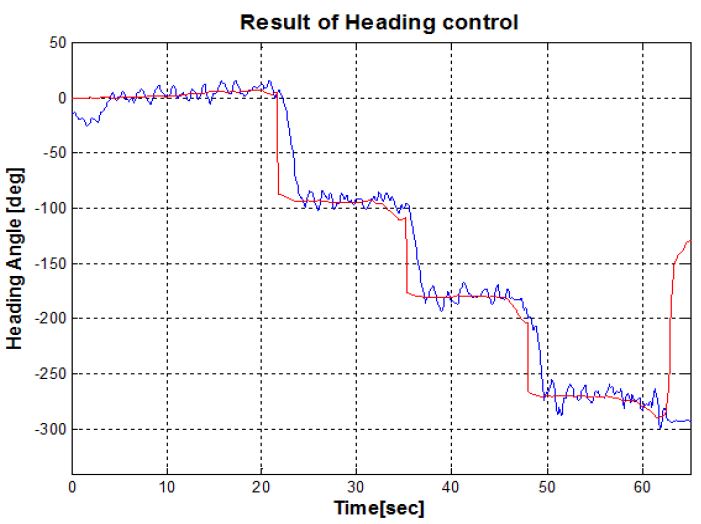
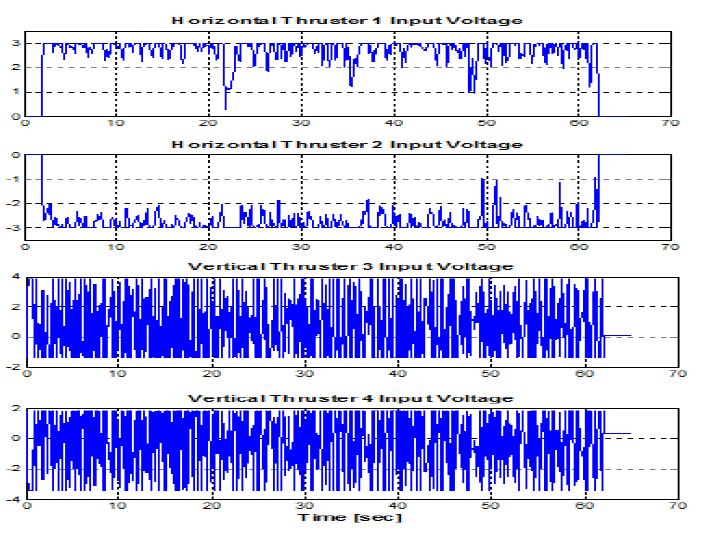
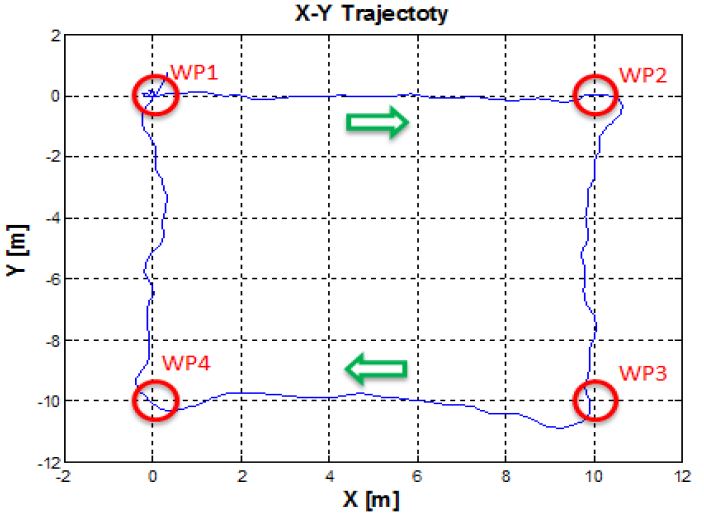
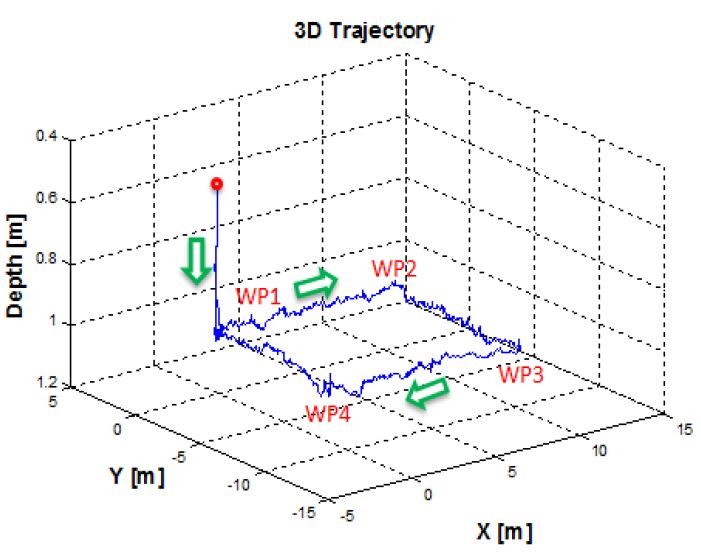
본 연구에서 수행한 경유점 제어는 (0,0,0)을 시작점으로 주어진 5개의 경유점(WP, Way-Point)을 통과하고 시작점으로 돌아오는 경로를 설정하였다. Figure 13은 DVL 센서에서 계측되는 무인잠수정의 속도를 적분하여 나타낸 이동거리이며, 무인잠수정의 X-Y평면의 경로를 나타낸다. 무인잠수정의 운동을 고려하여 정확한 경유점에 도달하는 것이 어렵기 때문에 유효반경(r = 0.5m)을 설정하여 실험하였다. DVL 오차분석에 관한 선행 실험을 통해 정수에서 0.5% 정도의 위치오차를 갖는 것을 확인 하였으며 본 실험에서는 DVL의 오차포함 위치 값을 실제 잠수정의 위치로 가정하였다. Figure 14는 무인잠수정의 3차원 경로를 나타내는 그래프로 초기 무인잠수정은 수심방향으로 1m 잠항하고, 이후 수심을 유지하면서 주어진 경유점을 돌아 다시 수면으로 부상하는 것을 확인 할 수 있다. Figure 15는 경유점 제어를 수행하는 동안 무인잠수정의 수심방향 제어 결과를 나타낸다. 목표수심에서 약 ±0.04m의 진동을 보이며 수심을 유지하는 것을 확인할 수 있다. Figure 16은 LOS방법을 통해 결정된 목표방향각의 변화에 따라 무인잠수정의 방향각 변화를 나타낸 그래프이다. 초기 약 -25°에서 출발한 무인잠수정은 첫번째 경유점으로 이동하기 위해 방향각을 설정한다. 이후 각각의 경유점으로 이동하기 위해 방향각을 설정하고 목표방향각의 일정범위 내에서 진동하며 추종하는 것을 확인 할 수 있다. 이는 계속적인 조류외란의 존재 하에서 목표값을 추종해가는 과정이 반복되는 것으로 생각된다. Figure 17은 설계된 추력분배 방법에 따라 무인잠수정이 주어진 목표를 수행하기 위해 추진기의 입력을 제어하는 것을 나타낸다. 앞서 설명한 추진기 구성행렬에 의해 수평추진기 및 수직추진기의 제어입력이 출력되는 것을 확인 할 수 있다.

Figure 13:

X-Y trajectory of hovering AUV

Figure 14:

3-D trajectory of hovering AUV

Figure 15:

Result of depth control

Figure 16:

Result of heading control

Figure 17:

Thrust control input voltage

5.2 Fuzzy PID 제어기

5.1절에 이어서 Fuzzy PD Controller를 설계하여 수심 제어와 방향각 제어 그리고 경유점 제어를 수행하였다. 이때 사용된 입력변수와 출력변수들의 소속 함수 및 퍼지규칙은 생략하였다.

5.2.1 수심제어

5.1.1과 유사한 조건에서 수심제어 실험을 수행하였다. 입력변수인 e_depth , $$ {\dot{e}}_{depth}$$의 범위를 크게 5구간NB(Negative Big), NS(Negative Small), S(Small), PS(Positive Small), PB(Positive Big)으로 나누었고 출력변수인 gain값의 범위는 크게 3구간(S, M, B)으로 나누었다. 다수의 실해역 실험을 통하여 Fuzzy rule을 수정하였고 Figure 18은 설계된 Fuzzy PID 제어기를 사용하여 100초 동안 수심제어를 수행한 결과 그래프를 나타낸다. 목표수심은 1m로 설정하였고 잠수정이 운동을 시작하고 약 5초 이후 정상 상태에 도달하는 것을 확인 할 수 있다. 약 ±2cm의 범위 내에서 목표수심을 잘 추종하고 있으며 이를 통해 Fuzzy 이론을 적용한 수심 제어기의 성능을 확인 하였다.

Figure 18:

Result of Fuzzy PID depth control

5.2.2 방향각 제어

경유점 제어를 수행하기 전 잠수정의 방향각 제어 실험을 수행하였다. 이때 입력변수인 e_yaw ,$$ {\dot{e}}_{yaw}$$의 범위를 수심제어와 마찬가지로 5구간으로 나누었고 출력변수는 3구간으로 나누었으며 반복된 실험으로 Fuzzy rule을 수정하였다. Figure 19는 설계된 Fuzzy PID 제어기를 사용하여 약 50초 동안 직진방향으로의 운동을 하며 방향각 제어를 수행한 결과 그래프를 나타낸다. 무인잠수정이 약 – 120°의 방향각을 가리키고 있는 상태에서 실험을 시작하였으며 약 10초 후 ± 3°이내의 오차를 가지며 목표 방향각인 0°를 잘 추종하는 결과를 보인다. 제어기 설계 시 설정한 목표오차 범위인 ± 5°이내에 수렴하는 결과로 Fuzzy PID 제어기의 성능을 검증하였다.

Figure 19:

Result of Fuzzy PID heading control

5.2.3 경유점 제어

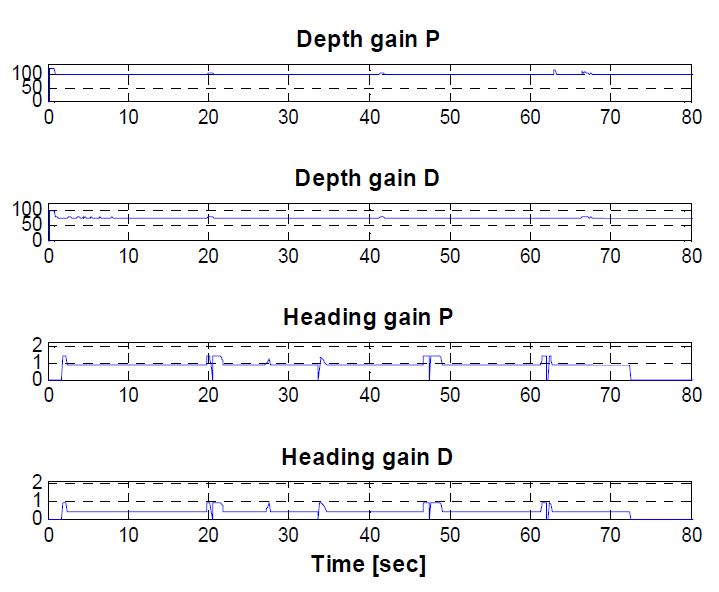
수심제어 및 방향각 제어의 결과로부터 Fuzzy PID 제어기의 성능을 검증하였고 무인잠수정의 X-Y 평면에서의 경로를 나타내는 Figure 20과 같이 경유점 제어를 수행하였다. 초기(0,0,0)의 위치를 앞서 정의한 WP1이라 하고 각각의 WP지점들을 경유하여 원래의 위치로 돌아오도록 경로를 설정하였다. Figure 21은 이를 3차원 경로로 나타낸 그래프로 수상에서 출발한 무인잠수정이 수심방향으로 1m 잠항한 뒤 수심을 유지하며 경유점을 경유하고 수면으로 부상하는 것을 확인할 수 있다. Figure 22는 잠수정의 수심방향 제어 결과 그래프로 목표 수심인 1m를 약 ±3cm의 오차를 가지며 추종하는 것을 확인할 수 있다. Figure 23은 이때의 방향각 제어 결과 그래프이며 무인잠수정이 약 50°의 초기 방향각에서 출발하여 목표 방향각을 추종하며 운동하는 것을 알 수 있다. 이때 발생하는 오차는 약 ±10°로 PID제어기를 사용한 실험 결과에 비해 개선된 경향을 보이나 5.2.2의 방향각 제어결과에 비해 좋지 않은 경향을 보이는 것을 알 수 있다. Figure 10에서 나타나듯이 수심제어 및 방향각 제어는 조류를 극복할 수 있는 내항에서 실험을 수행하였고, 경유점 제어는 내항이 협소하여 조류의 영향을 크게 받는 장소에서 실험을 수행하였다. 그 결과 조류의 영향을 받아 경유점 제어를 수행하였을 경우 내항의 실험결과보다 큰 약 ±10°의 오차를 지니는 것으로 판단된다. 이는 추가적인 추진기를 장착하고 조류와 같은 외란에 강인한 제어기를 설계함으로써 추후 극복해야 할 연구 과제이다. Figure 24는 설계된 Fuzzy PID제어기를 통해 얻은 수심제어 및 방향각 제어에 사용된 이득 값을 나타내는 그래프이다. 큰 e 와 $$ \dot{e}$$ 를 가지는 구간에서 설계한 Fuzzy rule에 의해 이득 값이 크게 변하는 것을 볼 수 있으며 정상상태에 도달하였을 경우 일정한 이득 값을 가지는 것을 확인할 수 있다. 이는 조류외란에 의해 섭동되는 시스템을 제어하기 위해 이득값이 변화하는 것을 나타내며 외란에 대한 강인한 성능을 나타낸다고 볼 수 있다.

Figure 20:

X-Y trajectory of hovering AUV

Figure 21:

3-D trajectory of hovering AUV

Figure 22:

Result of depth control

Figure 23:

Result of heading control

Figure 24:

Gain value

6. 결 론

본 논문에서는 실험이 용이하고 다양한 수중센서 테스트 및 제어 알고리듬의 성능 확인을 하기 위한 무인잠수정의 테스트 베드를 개발하였으며, 이를 활용해 무인잠수정의 기본 운동성능 실험과 경유점 제어 실험을 수행하였다. 또한 설계된 잠수정에 대한 운동성능 및 제어 알고리듬을 확인하기 위하여 수학적 모델을 이용한 동역학 시뮬레이션 프로그램을 구성하였으며, 설계된 제어기의 성능을 확인하는 연구를 수행하였다. 본 논문에서는 PID 제어기와 퍼지 논리에 의해 이득값 조정이 가능한 Fuzzy PID 제어기의 성능을 확인하는 수치 시뮬레이션을 수행하였다. 또한 추진기에 적절한 제어 입력 값을 분배하기 위한 제어력 분배방법을 적용하였다. 설계된 제어 알고리즘과 항법시스템을 이용하여 제작된 무인잠수정의 운동성능과 제어성능을 확인하기 위한 수심 제어, 방향각 제어 및 경유점 제어를 조류외란이 존재하는 실해역에서 수행하였으며 그 결과 어느 정도 타당한 제어성능을 얻을 수 있었다. 실해역 실험에서는 기초 실험을 위해 기본적인 PID 제어기와 설계한 퍼지 시스템의 규칙에 의해 외란(조류)에 실시간으로 이득값이 조정 가능한 Fuzzy PID 제어기를 사용하였으며, 실제로 강한 조류의 영향으로 PID 제어기의 이득 값을 튜닝하는 것이 매우 힘든 작업 중 하나였으며 Fuzzy PID의 경우 이러한 튜닝작업이 매우 편리하였다. 추후 정밀한 경로의 계측을 위한 필터설계 및 알고리즘 개발이 필요하고 강인한 제어기를 도입하여 실해역의 외란에도 강인하게 제어할 수 있는 방법에 관한 연구를 수행하고자 한다.

Acknowledgments

이 논문은 2015년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업 (2015R1D1A3A01015804)이며, 또한 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 산학협력 선도대학(LINC) 육성사업의 연구결과 중 일부임을 밝히며, 연구비 지원에 감사드립니다.

References

• B. H. Jun, P. M. Lee, and Y. K. Lim, “Trends in the Cruising-Type AUVs Technologies”, Journal of the Korean Society for Precision Engineering, 26(5), p14-22, (2009).
• S. K. Choi, J. Yuh, and G. Y. Takashige, “Development of the Omni Directional Intelligent Navigator”, IEEE Robotics & Automation Magazine, 2(1), p44-53, (1995). [https://doi.org/10.1109/100.388292]
• H. Kondo, T. Ura, S. C. Yu, and Y. Nose, “Design of Autonomous Underwater Vehicle Tri-Dog 1 and Tank Tests”, Proceedings of International Symposium Techno-Ocean, p339-244, (2000).
• J. Y. Kim, “Controller design for an autonomous underwater vehicle using estimated hydrodynamic coefficients”, Journal of Ocean Engineering and Technology, 20(6), p7-17, (2006).
• J. Y. Kim, “Design and control of a hovering type AUV”, Journal of the Korean Society for Precision Engineering, 26(5), p23-32, (2009).
• T. Fossen, Guidance and Control of Ocean Vehicles, Norway, John wiley & Sons Ltd, (1994).
• J. Garus, and J. Malecki, “A control allocation method for over-actuated underwater robot”, Proceedings of the 5th WSEAS Congress on Applied Computing Conference, and Proceedings of the 1st International Conference on Biologically Inspired Computation, World Scientific and Engineering Academy and Society (WSEAS), p74-79, (2012).
• J. Garus, “Optimization of thrust allocation in the propulsion system of an underwater vehicle”, International Journal of Applied Mathematics and Computer Science, 14(4), p461-467, (2004).
• O. J. Sordalen, “Optimal thrust allocation for marine vessels”, Control Engineering Pratice, 5(9), p1223-1231, (1997). [https://doi.org/10.1016/S0967-0661(97)84361-4]