핀치포인트온도차에 따른 해양온도차발전용 유기랭킨사이클의 성능분석

1. 서 론

전 세계적으로 에너지 고갈 및 환경오염 문제에 대한 관심이 날로 커지고 있다[1]. 이러한 문제를 해결하기 위해 지구표면의 70%를 차지하는 해양을 이용한 친환경적인 에너지를 생성하는 방안이 고려되고 있다[2]. 해양에너지기술 중 하나인 해양온도차발전(OTEC; Ocean Thermal Energy Conversion)은 태양에너지를 흡수한 표층수와 수심 1,000m 이하의 심층수의 온도차를 이용하여 발전하는 동력 사이클이다[3].

태양으로부터 흡수된 해양온도차에너지의 부존량은 매년 인류가 요구하는 에너지의 약 4,000배에 달한다[4]. 그러나 해양온도차발전은 저온의 열원을 이용하므로 작동유체를 물을 사용하는 기존의 증기동력 사이클을 적용할 경우 팽창기의 구동에 필요한 팽창비를 확보할 수가 없다. 따라서 물에 비해 비등점이 매우 낮은 유기냉매 또는 탄화수소 화합물을 작동유체로 이용하는 유기랭킨사이클(ORC; Organic Rankine Cycle)의 사용이 불가피하다[3]. 해양온도차발전용 유기랭킨사이클은 열원과 열침의 온도차가 20℃, 시스템 효율이 약 3-5%에 불과하므로 보다 경제적이고 효과적인 기술연구가 필요하다[5][6].

작동유체 선정은 해양온도차발전용 유기랭킨사이클의 열역학적 성능에 큰 영향을 준다[7]. 해양온도차발전용 작동유체로는 고전적 순수유체 NH3와 R22가 사용되어 왔으나 NH3는 인화성 및 독성에 대한 문제가 있으며, CFC 및 HCFC 계열의 유기냉매의 사용은 몬트리올 의정서에 의해 규제되었다. 한편, Wang et al. [7], Tchanche et al. [8], Le et al. [9]은 유기랭킨사이클에 적합한 작동유체의 선정에 대한 연구를 수행하였다.

유기랭킨사이클의 열역학적 분석 방법으로 핀치포인트 온도차(PPTD; Pinch Point Temperature Difference)를 이용하는 연구가 있다[10]-[13]. PPTD는 열교환기에서의 열원 혹은 열침과 작동유체의 최소온도차이며, 열교환기의 규모와 비용을 결정하는데 있어 큰 영향을 미친다[10]. 또한 PPTD와 열원 및 열침의 온도변화는 사이클의 증발온도 및 응축온도를 결정한다. 이와 같이 PPTD를 이용한 열역학적 사이클 해석방법을 핀치포인트분석(PPA; Pinch Point Analysis)이라고 한다[13].

어떤 계가 주어진 상태에서 과정을 겪을 때 얻을 수 있는 최대 유용일을 엑서지(exergy)라고 하며, 열역학적 사이클 분석에 있어 엑서지를 반영한 유기랭킨사이클의 제2법칙 효율(second law efficiency)은 사이클 성능을 결정하는 중요한 척도가 된다[14]. 따라서 비가역성의 결과로 과정동안 폐기된 잠재일로 정의하는 엑서지 파괴에 대한 연구가 있었으며[15]-[17], 특히 Shengjun et al. [15]은 엑서지 파괴인자(EDF; Exergy Destruction Factor)를 정의하여 각 기기의 엑서지 파괴인자에 대해 분석 연구한 결과를 보였다. 한편, Wang et al. [13]의 연구에서는 폐열회수용 유기랭킨사이클에서 PPTD와 열원 출구측 온도변화에 따른 사이클 성능변화에 대해 연구함으로써 상기의 독립변수가 유기랭킨사이클에 미치는 영향에 대해 파악할 수 있는 연구를 하였다.

본 연구의 목적은 해양온도차발전용 유기랭킨사이클에 다양한 작동유체를 적용하여 각 열교환기 측의 PPTD의 영향에 따른 열역학적 사이클의 다양한 성능결과를 분석함으로써 보다 적합한 열역학적 상태를 파악하는 것이다. 사이클 분석도구로는 열역학적 공정 및 사이클의 상용설계프로그램인 HYSYS를 사용하였다. HYSYS를 통해 여러 가지 사이클 설계인자를 반영하여 해양온도차발전의 일반적인 운전조건에 준하는 열역학적 사이클을 모사하였으며, 다양한 작동유체를 모사한 사이클에 적용함으로써 사이클 성능을 연구하였다.

2. 해양온도차발전용 사이클 해석

2.1 열역학적 사이클

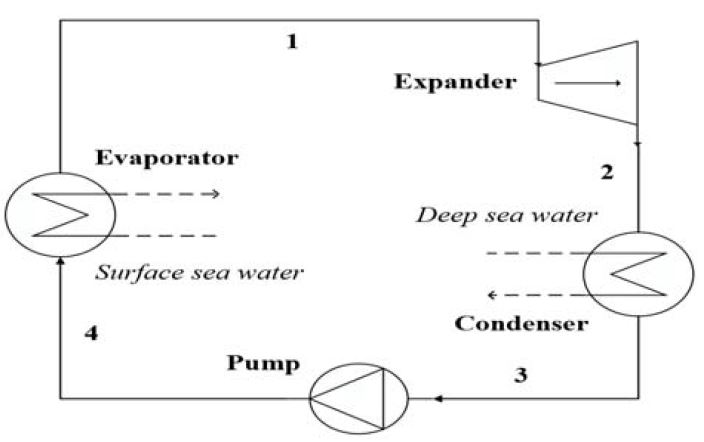
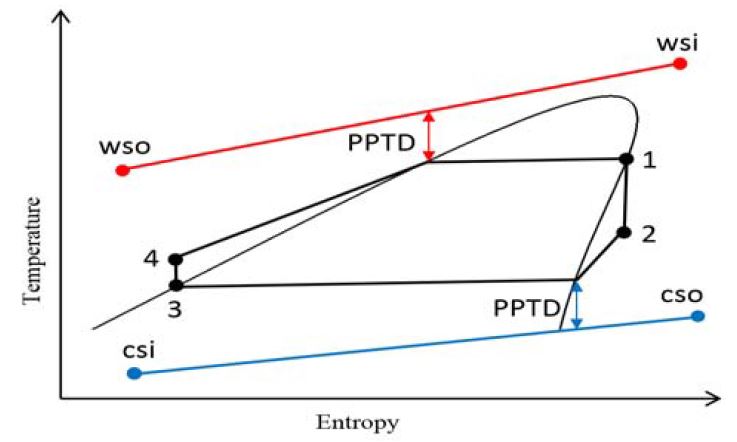
Figure 1과 2는 해양온도차발전용 단순 랭킨사이클의 개략도와 T-s 선도를 나타내고 있다. 1번 지점의 증기상태작동유체는 이상적인 터빈으로 유입되는 경우 등엔트로피 팽창을 한다. 2번 지점의 팽창된 증기는 응축기에서 심층수와 열교환하여 응축이 된다. 이상적인 경우, 3번 지점의 응축액은 펌프에 유입되어 증발압력까지 등엔트로피적으로 압력이 상승된다. 4번 지점의 작동유체는 증발기에서 표층수에 의해 1번 지점까지 가열되어 터빈 입구 상태까지 사이클이 완성된다[18]. 여기서, 각각의 열역학적 상태는 에너지 및 엑서지 분석을 기초로 한 열역학 제1법칙 및 제2법칙에 따라 다음과 같은 수식으로 표현한다.

Figure 1:

Schematic diagram of the simple Rankine cycle

Figure 2:

T-s diagram of the simple Rankine cycle

식(1)~(2)는 터빈, 식(3)~(4)는 응축기, 식(5)~(6)은 펌프, 식(7)~(8)은 증발기에서 각각의 단위 시간당 에너지와 엑서지 파괴율을 나타낸다. 식 (9)는 사이클의 비가역성($$ {\dot{I}}_{total}$$)을 나타내는 식이며, 이 값은 각 상태에서 엑서지 파괴율의 합과 같다. 식 (10)은 사이클 효율(η_th)을 의미하며, 식 (11)은 식 (10)에서 구한 사이클 효율(η_th)을 가역 효율로 나눈 값이다. 이 값을 제2법칙 효율(η_Π) 혹은 엑서지 효율(exergy efficiency)이라고 한다. T₀는 주위의 온도를 의미한다. 또한 Wang et al. [13]의 연구를 참조하여T_H 및 T_L 는 식 (12)~(13)으로 정의한다. 식 (12)에서 T_pp는 증발기에서 열원과 작동유체의 최소온도차상태일 때 열원측 온도를 의미한다.

$\[ {\dot{W}}_t=\dot{m}\left(h_1-h_2\right){\eta }_t \]$

(1)

$\[ {\dot{I}}_t=T_0\dot{m}\left(s_2-s_1\right) \]$

(2)

$\[ {\dot{Q}}_c=\dot{m}\left(h_2-h_3\right) \]$

(3)

$\[ {\dot{I}}_c=T_0\dot{m}\left\{\left(s_3-s_2\right)-\frac{\left(h_3-h_2\right)}{T_L}\right\} \]$

(4)

$\[ {\dot{W}}_p=\dot{m}\left(h_4-h_3\right)/{\eta }_p \]$

(5)

$\[ {\dot{I}}_p=T_0\dot{m}\left(s_4-s_3\right) \]$

(6)

$\[ {\dot{Q}}_e=\dot{m}\left(h_1-h_4\right) \]$

(7)

$\[ {\dot{I}}_e=T_0\dot{m}\left\{\left(s_1-s_4\right)-\frac{\left(h_1-h_4\right)}{T_H}\right\} \]$

(8)

$\[ {\dot{I}}_{total}=T_0\dot{m}\left\{-\frac{\left(h_1-h_4\right)}{T_H}-\frac{\left(h_3-h_2\right)}{T_L}\right\} \]$

(9)

$\[ {\eta }_{th}=\frac{{\dot{W}}_t-{\dot{W}}_p}{{\dot{Q}}_e} \]$

(10)

$\[ {\eta }_{\mathrm{\Pi }}={\eta }_{th}{\left(1-\frac{T_L}{T_H}\right)}^{-1} \]$

(11)

$\[ T_H=\frac{T_{\omega si}+T_{pp}}{2} \]$

(12)

$\[ T_L=\frac{T_{csi}+T_{cso}}{2} \]$

(13)

Shengjun et al. [15]의 연구를 참조하여 제2법칙 효율을 EDF로부터 구할 수 있다. 식 (14)~(17)을 통해 터빈, 응축기, 펌프, 증발기에서 각각의 엑서지 파괴율을 정미출력동력으로 나누어 EDF를 구할 수 있다. 그리고 식 (18)~(19)를 보면 각각의 EDF 값들을 합하여 사이클의 총 엑서지 파괴인자(EDF_total)를 구할 수 있으며, 이 값을 이용하여 제2법칙 효율을 산출할 수 있다.

$\[ ED{F}_t=\frac{{\dot{I}}_t}{{\dot{W}}_t-{\dot{W}}_p} \]$

(14)

$\[ ED{F}_c=\frac{{\dot{I}}_c}{{\dot{W}}_t-{\dot{W}}_p} \]$

(15)

$\[ ED{F}_p=\frac{{\dot{I}}_p}{{\dot{W}}_t-{\dot{W}}_p} \]$

(16)

$\[ ED{F}_e=\frac{{\dot{I}}_e}{{\dot{W}}_t-{\dot{W}}_p} \]$

(17)

$\[ ED{F}_{total}=ED{F}_t+ED{F}_c+ED{F}_p+ED{F}_e \]$

(18)

$\[ {\eta }_{\mathrm{\Pi }}=\frac{1}{1+ED{F}_{total}} \]$

(19)

2.2 해석조건

2.2.1 기본설계조건

본 연구의 기본적인 열역학적 사이클의 설계조건은 Kim et al. [18]의 연구를 참조하였으며, 설계인자는 Table 1과 같다. 일정한 표층수와 심층수의 온도변화와 증발기 및 응축기의 PPTD를 일정하게 유지함으로써 사이클의 증발온도와 응축온도를 결정한다. 증발기의 출구측 상태는 포화증기, 응축기출구측 상태는 포화액 상태로 가정하였다. 사이클의 질량유량을 결정하기 위해 증발기에 유입되는 표층수 유량을 일정하게 가정하였으며, 열교환기 내에서의 압력강하는 무시하였다. 터빈과 펌프의 효율은 각각 85%, 80%로 가정하였으며, 주위 공기의 온도는 20℃로 가정하였다.

Table 1:

Basic design parameters for the thermodynamic cycle

2.2.2 작동유체의 선정

본 연구에서는 Kim 등[18]의 연구에서 엄밀히 선정한 작동유체를 참조하였다. Le 등[9]에 의하면 전 세계적으로 지구온난화지수(GWP; Global Warming Potential)에 대한 규제가 강화되는 추세이므로, 본 연구에서는 GWP가 1500 이하인 작동유체로 선별하였다. 선정한 7종의 작동유체는 Table 2와 같다. 여기서 선정된 작동유체는 dry fluid, isentropic fluid 및 wet fluid로 분류되며, 각각 포화증기선의 기울기가 양수, 무한대 그리고 음수이다. Table 3는 Table 2에 명시된ASHRAE 안전등급에 대해 나타낸다. 본 연구에서는 독성 및 가연성이 낮은 A1, A2 그룹의 작동유체를 선별하였으며, ASHRAE 안전등급이 알려지지 않은 작동유체는 무독성, 무가연성 작동유체로 취급하였다.

Table 2:

Information of the working fluids

Table 3:

Safety classifications according to the ASHRAE safety group

2.2.3 Peng-Robinson 방정식

이상기체 상태방정식은 간단하나 그 적용범위가 제한되어 있으므로 보다 정밀하게 물질의 상태를 나타내기 위한 실제기체 상태방정식들이 제안되고 있다[19]. 본 연구에서는 다수의 실제기체 상태방정식 중 Peng-Robinson 방정식을 사용하였다.

$\[ p=\frac{RT}{V_m-b}-\frac{a\alpha }{V_m^2+2b{V}_m-b^2} \]$

(20)

$\[ a=\frac{0.457235R^2{T}_c^2}{p_c} \]$

(21)

$\[ b=\frac{0.077796R{T}_c}{p_c} \]$

(22)

$\[ \alpha ={\left(1+\kappa \left(1-T_r^{0.5}\right)\right)}^2 \]$

(23)

$\[ \kappa =0.37464+1.54226\omega -0.26992{\omega }^2 \]$

(24)

$\[ T_r=\frac{T}{T_c} \]$

(25)

여기서, 임계점에서의 온도(T_c)와 압력(p_c) 그리고 기체상수(R)를 이용하여 식 (21) ~ (22)에서 a와 b값을 계산할 수 있다. 식 (24)에서 무중심 입자(ω)를 이용해 κ값을 구할 수 있으며, 식 (25)에서 임계점에서의 온도(T_c)와 절대온도(T)를 이용해 T_r값을 구할 수 있다. 식(24) ~ (25)에서 구한 κ 와 T_r 을 이용해 식 (23)에서 α값을 산출할 수 있다. 이렇게 구해진 값과 액체의 단위 몰부피(V_m)를 이용하면 식 (20)과 같이 기체의 절대 압력(p)을 유도할 수 있다.

3. 결과 및 고찰

3.1 증발기측 PPTD의 영향

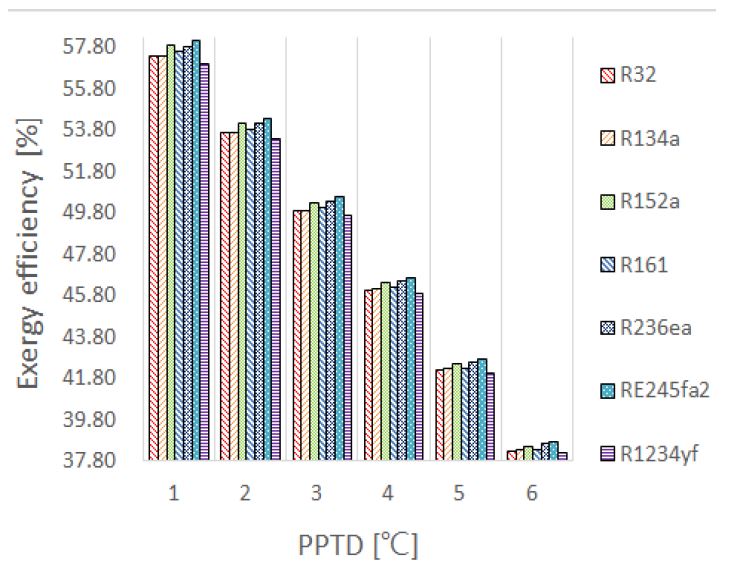
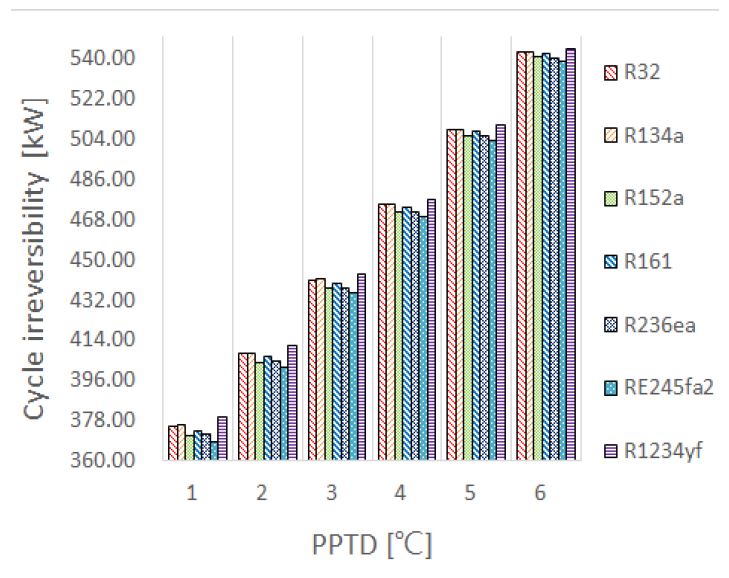
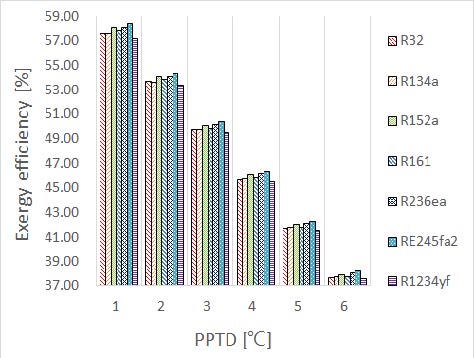
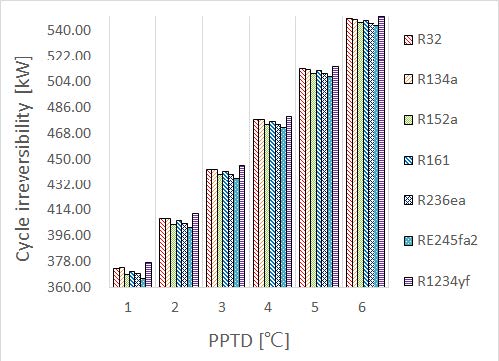
Figure 3, Figure 4는 기본설계조건에서 각각 증발기측 PPTD 변화에 따른 제2법칙 효율(η_Π) 및 사이클 비가역성($$ {\dot{I}}_{total}$$)을 나타낸다. 증발기측 열원의 입출구 온도변화가 일정한 경우, PPTD의 값이 커질수록 증발온도가 하강하며 PPTD의 값이 작아질수록 증발온도가 상승한다. 본 연구의 설계조건에 따라 PPTD가 1℃인 경우를 PPTD가 6℃인 경우와 비교해보면 증발온도가 상승할시 증발압력 또한 상승한다. 증발압력이 상승할 경우, 정미출력일 및 사이클 효율(η_th)이 커진다[19]. 가역 효율은 T_H 및 T_L 이 거의 일정하므로, 제2법칙 효율(η_Π)은 사이클 효율(η_th)에 비례하여 상승하는 반면 사이클의 비가역성($$ {\dot{I}}_{total}$$)은 작아진다. 이는 폐열회수용 유기랭킨사이클에서 증발기측 PPTD 변화에 따른 연구결과[13]와 흡사하며, 해양온도차발전용 유기랭킨사이클의 낮은 온도범위 열원에서도 엑서지 파괴로 인한 비가역성의 차이가 확연하게 보인다. 작동유체간의 성능에 대해 살펴보면 제2법칙 효율(η_Π) 및 사이클 비가역성($$ {\dot{I}}_{total}$$)면에서 큰 차이는 없었으며, 선정한 작동유체 중에서는 RE245fa2가 가장 우수하였다.

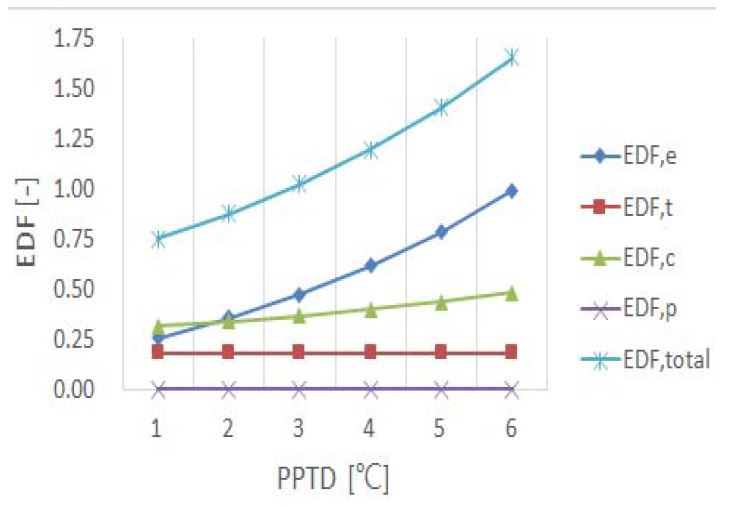
Figure 5는 열역학적 성능이 가장 우수한 RE245fa2를 식 (14)~(18)에 적용하여 PPTD 에 따른 EDF의 변화에 대해 나타낸 것이다. Figure 4를 참조하면 PPTD가 상승함에 따라 사이클 비가역성($$ {\dot{I}}_{total}$$)이 상승하며, 총 엑서지 파괴인자(EDF_total) 또한 0.75에서 1.66으로 상승함을 알 수 있다. 각 기기별 엑서지 파괴에 대한 연구 결과가 있는 Le et al. [9], Wei et al. [17]의 연구를 참조하여, 각 기기별 EDF 변화에 대해 살펴보면 증발기측 EDF의 값(EDF_e)이 0.25에서 0.99로 크게 상승하였다. 반면 응축기측 EDF의 값(EDF_c)은 0.32에서 0.48로 다소 소폭 상승하였다. 이러한 이유는 증발 기측 PPTD의 변화가 증발기 엔트로피 생성(Sgen)에 대해 큰 영향을 주기 때문이다. 즉, 증발기측 PPTD가 증가할수록 타 기기에 비해 증발기에서 엔트로피 생성량이 크게 증가하며, EDF의 값도 크게 상승한다. 이러한 결과는 모든 작동유체에서 유사한 결과를 보였다.

Figure 3:

Exergy efficiency with respect to the PPTD at evaporator

Figure 4:

Cycle irreversibility with respect to the PPTD at evaporator

Figure 5:

EDF of RE245fa2 with respect to the PPTD at evaporator

3.2 응축기측 PPTD의 영향

Figure 6 과 Figure 7은 기본설계조건에서 각각 응축기측 PPTD 변화에 따른 제2법칙 효율(η_Π) 및 사이클 비가역성($$ {\dot{I}}_{total}$$)을 나타낸다. 응축기측 열침의 입출구 온도변화가 일정한 경우, PPTD의 값이 커질수록 응축온도가 상승하며 PPTD의 값이 작아질수록 응축온도가 하강한다. 응축온도가 하강하게 되면, 응축압력이 낮아지므로 정미출력일 및 사이클 효율이 커진다[19]. 따라서 증발기측 PPTD 변화에 따른 결과와 마찬가지로 모든 작동유체가 PPTD의 값이 커질수록 사이클 효율(η_th) 및 제2법칙효율(η_Π)의 값은 작아지는 반면 사이클의 비가역성($$ {\dot{I}}_{total}$$)은 커진다. Li et al. [10]과 Wang et al. [13]의 연구에서는 유기랭킨사이클에 있어 증발기측 PPTD의 값이 사이클 성능에 미치는 영향에 대한 연구 결과만 언급되어 있으나, 본 연구의 설계조건에 따른 해양온도차발전용 유기랭킨사이클의 경우 응축기측 PPTD의 변화에도 사이클에 성능에 큰 영향을 미친다는 점을 알 수 있었다.

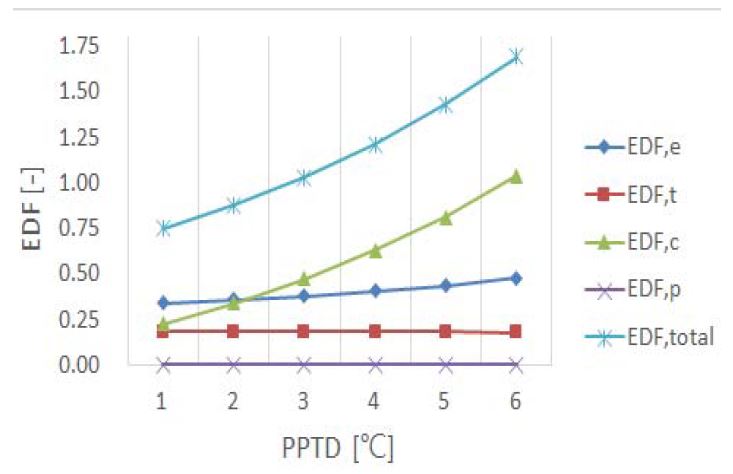
Figure 8은 Figure 5와 같이 작동유체 RE245fa2를 사용한 사이클에서 응축기의 PPTD 변화에 따른 각 기기별 EDF 변화를 나타낸다. Figure 5와 비교하면 PPTD의 값이 증가할수록 사이클 비가역성이 커지므로, 총 엑서지 파괴인자(EDF_total)의 값이 0.75에서 1.69로 상승한다. Figure 5에서는 증발기의 EDF 값(EDF_e)이 크게 증가한 반면, Figure 8에서는 응축기의 EDF 값(EDF_c)이 0.23에서 1.04로 크게 증가하였으며, 증발기의 EDF 값(EDF_e)은 0.34에서 0.48로 소폭 상승하였다. 이 결과로 사이클의 엑서지 파괴인자(EDF_total)의 값이 상승하더라도 PPTD 변화가 발생하는 위치에서 엔트로피 생성량(S_gen)이 크게 증가하며, EDF의 값 또한 크게 상승함을 알 수 있다. 이러한 결과는 선정한 작동유체에서 비슷한 결과를 보였다.

Figure 6:

Exergy efficiency with respect to the PPTD at condenser

Figure 7:

Cycle irreversibility with respect to the PPTD at condenser

Figure 8:

EDF of RE245fa2 with respect to the PPTD at condenser

3.3 열원 및 열침 출구온도의 영향

Guo et al. [12]과 Wang et al. [13]의 연구에 의하면, 열원의 입구온도 및 증발기측 PPTD의 값은 고정한 상태에서 열원의 출구온도 변화에 의해서도 유기랭킨사이클 성능이 크게 변화됨을 알 수 있다. 본 연구에서는 상기의 연구를 참조하여, 기본설계조건에 따른 사이클에 RE245fa2를 적용하여 각 열교환기의 PPTD의 값은 2℃로 고정한 상태에서 열원 및 열침출구온도 변화에 따른 EDF값의 변화에 대해 살펴보았다.

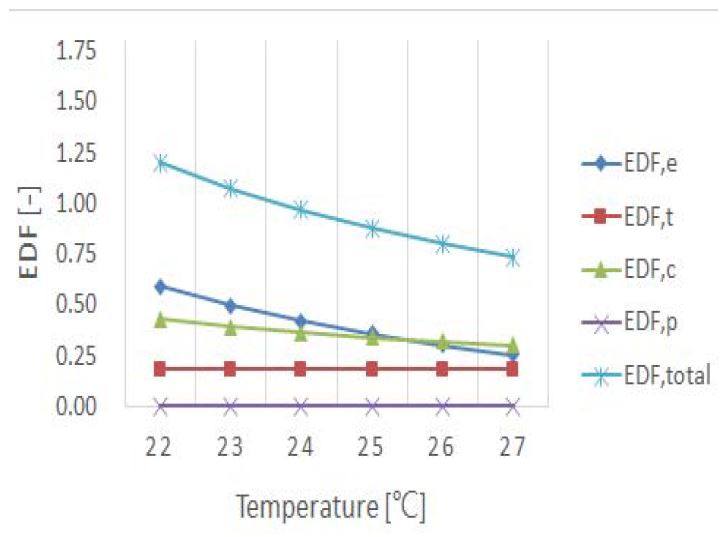
Figure 9는 열원의 출구온도 변화에 따른 RE245fa2의 EDF변화를 나타낸다. 총 엑서지 파괴인자(EDF_total)의 값은 1.20에서 0.74로 감소하였다. PPTD가 고정된 상태에서 열원의 출구온도가 상승하면 증발온도 및 증발압력이 상승하여 사이클 효율(η_th) 및 제2법칙효율(η_Π)은 증가하는 반면 비가역성($$ {\dot{I}}_{total}$$) 및 EDF값은 감소함을 알 수 있다. 여기서, 증발기의 EDF값(EDF_e)은 0.59에서 0.25로 크게 감소하였으며, 응축기의 EDF값(EDF_c)은 0.43에서 0.30으로 비교적 작게 감소하였다. 이러한 결과로 다른 기기들보다 열원의 온도변화에 직접적인 영향을 미치는 증발기의 비가역성($$ {\dot{I}}_{total}$$)이 크게 떨어짐을 알 수 있다. 이러한 이유는 열원의 출구온도가 증가함에 따라 증발기에서 엔트로피 생성량(Sgen)이 크게 감소하기 때문이다.

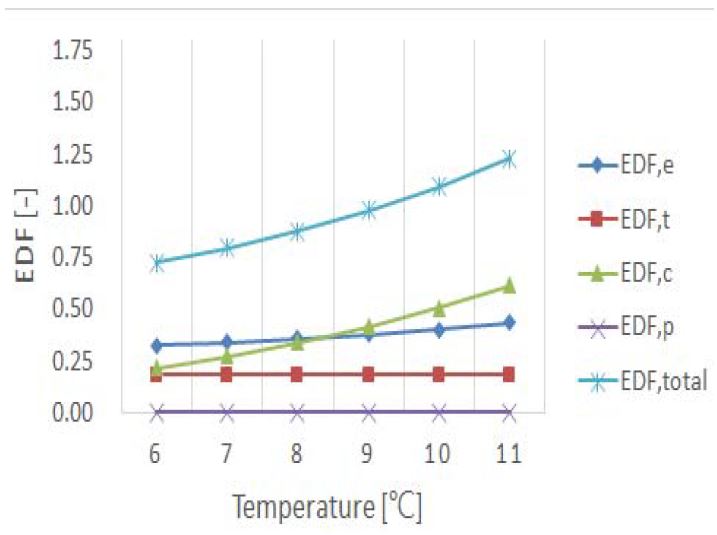
Figure 10은 열침의 출구온도 변화에 따른 RE245fa2의 EDF변화를 나타낸다. 총 엑서지 파괴인자(EDF_total)의 값은 0.72에서 1.23으로 증가하였다. PPTD가 고정된 상태에서 열침의 출구온도가 상승하면 응축온도 및 응축압력이 상승하여 사이클 효율(η_th) 및 제2법칙효율(η_Π)은 감소하는 반면 비가역성($$ {\dot{I}}_{total}$$) 및 EDF값은 증가함을 알 수 있다. 여기서, 증발기의 EDF값(EDF_e)은 0.32에서 0.43으로 작게 증가하였으며, 응축기의 EDF값(EDF_c)은 0.22에서 0.61로 비교적 크게 증가하였다. 이러한 결과로 다른 기기들보다 열침의 온도변화에 직접적인 영향을 미치는 응축기의 비가역성($$ {\dot{I}}_{total}$$)이 크게 상승함을 알 수 있다. 즉, 열침의 출구온도 변화에 따른 응축기의 엔트로피 생성량(Sgen)이 가장 크기 때문이다.

Figure 9:

EDF of RE245fa2 with respect to the outlet temperature of heat source with PPTD = 2℃

Figure 10:

EDF of RE245fa2 with respect to the outlet temperature of heat sink with PPTD = 2℃

5. 결 론

해양온도차발전용 유기랭킨사이클에 엄밀히 선정한 7종의 작동유체를 적용하여 열역학적 성능을 분석하였다. 증발기 및 응축기측의 일정한 열원 및 열침의 입출구 온도차에서 PPTD의 값이 작을수록, 고정된 PPTD에서는 입출구온도차가 작을수록 사이클 비가역성($$ {\dot{I}}_{total}$$) 및 총 엑서지 파괴인자(EDF_total)가 감소하며, 제2법칙 효율(η_Π)은 상승함을 알 수 있었다. 또한 온도변화가 발생한 곳에서 엔트로피 생성(Sgen)의 변화가 크므로 비가역성이 크게 변화하였다. 상기의 결과를 참조하여 열교환기의 PPTD 및 열원 및 열침의 온도차를 이용하여 우수한 열역학적 성능을 가진 열교환기를 고려할 수 있다. 그러나 Yang 등[3]과 Li 등[10]의 언급대로 열교환기에서 열원 혹은 열침과 작동유체의 온도차가 작을수록 열전달면적이 커지게 되며, 유기랭킨사이클의 구성비용이 상승한다. 따라서 해양온도차발전용 유기랭킨사이클의 열교환기를 선정할시 효율성 및 경제성에 대한 엄밀한 검토가 요구된다.

본 연구의 운전조건에서 선정한 작동유체 중 제2법칙 효율(η_Π) 및 사이클 총 비가역성($$ {\dot{I}}_{total}$$)면에서 RE245fa2가 가장 우수하였으나, 모든 작동유체가 본 연구의 독립변수에 따른 열역학적 성능변화는 큰 차이가 없었다. 유사한 열역학적 성능을 보이는 작동유체를 고려할 시에는 보다 더 친환경적이며, 안정성 있고, 경제성이 있는 작동유체의 선정하는 것이 바람직 할 것으로 보인다.

Acknowledgments

본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다. (No. 20133030000110)

References

• F. Sun, Y. Ikegami, B. Jia, and H. Arima, “Optimization design and exergy analysis of organic rankine cycle in ocean thermal energy conversion”, Journal of the Applied Ocean Research, 35, p38-46, (2012). [https://doi.org/10.1016/j.apor.2011.12.006]
• B. F. Tchanche, M. Petrissans, and G. Papadakis, “Heat resources and organic Rankine cycle machines”, Journal of the Renewable and Sustainable Energy Reviews, 39, p1185-1199, (2014). [https://doi.org/10.1016/j.rser.2014.07.139]
• M. H. Yang, and R. H. Yeh, “Analysis of optimization in an OTEC plant using organic Rankine cycle”, Journal of the Renewable Energy, 68, p25-34, (2014). [https://doi.org/10.1016/j.renene.2014.01.029]
• L. A. Vega, “Ocean thermal energy conversion primer”, Journal of the Marine Technology Society, 6(4), p25-35, (2003). [https://doi.org/10.4031/002533202787908626]
• B. F. Tchanche, G. Lambrinos, A. Frangoudakis, and G. Papadakis, “Low-grade heat conversion into power using organic Rankine cycles - A review of various applications”, Journal of the Renewable and Sustainable Energy Reviews, 15(8), p3963-3979, (2011). [https://doi.org/10.1016/j.rser.2011.07.024]
• R. Soto, and J. Vergara, “Thermal power plant efficiency enhancement with Ocean Thermal Energy Conversion”, Journal of the Applied Thermal Engineering, 62(1), p105-112, (2014). [https://doi.org/10.1016/j.applthermaleng.2013.09.025]
• E. H. Wang, H. G. Zhang, B. Y. Fan, M. G. Ouyang, Y. Zhao, and Q. H. Mu, “Study of working fluid selection of organic Rankine cycle (ORC) for engine waste heat recovery”, Journal of the Energy, 36(5), p3406-3418, (2011). [https://doi.org/10.1016/j.energy.2011.03.041]
• B. F. Tchanche, G. Papadakis, G. Lambrinos, and A. Frangoudakis, “Fluid selection for a low-temperature solar organic Rankine cycle”, Journal of the Applied Thermal Engineering, 29(11-12), p2468-2476, (2009). [https://doi.org/10.1016/j.applthermaleng.2008.12.025]
• V. L. Le, M. Feidt, A. Kheiri, and S. P. Prayer, “Performance optimization of low-temperature power generation by supercritical ORCs (organic Rankine cycles) using low GWP (global warming potential)”, Journal of the Energy, 67, p513-526, (2014). [https://doi.org/10.1016/j.energy.2013.12.027]
• Y. Li, J. Wang, and M. Du, “Influence of coupled pinch point temperature difference and evaporation temperature on performance of organic Rankine cycle”, Journal of the Energy, 42(1), p503-509, (2012). [https://doi.org/10.1016/j.energy.2012.03.018]
• H. Aydin, H. S. Lee, H. J. Kim, S. K. Shin, and K. Park, “Off-design performance analysis of a closed-cycle ocean thermal energy conversion system with solar thermal preheating and superheating”, Journal of the Renewable Energy, 72, p154-163, (2014). [https://doi.org/10.1016/j.renene.2014.07.001]
• C. Guo, X. Du, L. Yang, and Y. Yang, “Performance analysis of organic Rankine cycle based on location of heat transfer pinch point in evaporator”, Journal of the Applied Thermal Engineering, 62(1), p176-186, (2014). [https://doi.org/10.1016/j.applthermaleng.2013.09.036]
• D. Wang, X. Ling, and H. Peng, “Performance analysis of double organic Rankine cycle for discontinuous low temperature waste heat recovery”, Journal of the Applied Thermal Engineering, 48, p63-71, (2012). [https://doi.org/10.1016/j.applthermaleng.2012.04.017]
• M. Yari, A. Mehr, V. Zare, S. Mahmoudi, and M. Rosen, “Exergoeconomic comparison of TLC (trilateral Rankine cycle), ORC(organic Rankine cycle) and Kalina cycle using a low grade heat source”, Journal of the Energy, 83, p712-722, (2015). [https://doi.org/10.1016/j.energy.2015.02.080]
• Z. Shengjun, W. Huaixin, and G. Tao, “Performance comparison and parametric optimization of subcritical Organic Rankine Cycle (ORC) and transcritical power cycle system for low-temperature geothermal power generation”, Journal of the Applied Energy, 88(8), p2740-2754, (2011). [https://doi.org/10.1016/j.apenergy.2011.02.034]
• K. A. Barse, and M. D. Mann, “Maximizing ORC performance with optimal match of working fluid with system design”, Journal of the Applied Thermal Engineering, 100, p11-19, (2016). [https://doi.org/10.1016/j.applthermaleng.2016.01.167]
• D. Wei, X. Lu, Z. Lu, and J. Gu, “Performance analysis and optimization of organic Rankine cycle (ORC) for waste heat recovery”, Journal of the Energy Conversion and Management, 48(4), p1113-1119, (2007). [https://doi.org/10.1016/j.enconman.2006.10.020]
• J. S. Kim, D. Y. Kim, Y. T. Kim, and H. K. Kang, “Performance analysis of an organic Rankine cycle for ocean thermal energy conversion system according to the working fluid and the cycle”, Journal of the Korean Society of Marine Engineering, 39(9), p881-889, (2015). [https://doi.org/10.5916/jkosme.2015.39.9.881]
• Y. A. Cengel, and M. A. Boles, Thermodynamics, Seoul, South Korea, McGraw-Hill Education Korea, (2011).