[ Original Paper ]

Journal of the Korean Society of Marine Engineering - Vol. 40, No. 4, pp.369-373

ISSN: 2234-7925 (Print) 2234-8352 (Online)

Print publication date May 2016

Received 07 Jan 2016 Revised 08 Apr 2016 Accepted 18 Apr 2016

DOI: https://doi.org/10.5916/jkosme.2016.40.4.369

주파수 응답 데이터를 이용한 비비례 점성감쇠행렬 추정

민천홍^†

; 김형우²

Nonproportional viscous damping matrix identification using frequency response functions

Cheon-Hong Min^†

; Hyung-Woo Kim²

2Technology Center for Offshore Plant Industries, Korea Research Institute of Ships & Ocean Engineering, Tel: 042-866-3871 hyungwoo4601@kriso.re.kr

Correspondence to: ^†Technology Center for Offshore Plant Industries, Korea Research Institute of Ships & Ocean Engineering, Yuseong-gu, Daejeon, 305-343, Korea, E-mail: chmin@kriso.re.kr, Tel: 042-866-3886

Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록

감쇠구조물의 해석을 위해서는 정확한 감쇠모델을 구성하는 것이 중요하지만, 감쇠특성을 모델링 하는 것은 매우 어려운 일이다. 부정확한 감쇠 모델링에서 기인하는 오차는 진동 소음 문제 및 구조물 안전 평가 등에 많은 어려움을 주고 있다. 본 연구에서는 주파수 응답함수를 이용한 비비례 점성감쇠행렬 추정기법을 제시하였다. 복소 주파수 응답함수는 구조물의 실험데이터로부터 계측되며, 정상상태 주파수 응답함수는 계측된 복소 주파수 응답함수로부터 추정된다. 제안된 기법을 통해 비비례 점성감쇠 행렬을 추정하였으며, 두 가지 수치 예제(집중질량 모델과 외팔보)를 통해 제시된 기법을 검토하였다. 결과적으로 두 가지 예제 모두에서 비비례 점성감쇠 행렬을 정확히 추정할 수 있었다.

Abstract

Accurate identification of damping matrix in structures is very important for predicting vibration responses and estimating parameters or other characteristics affected by energy dissipation. In this paper, damping matrix identification method that use normal frequency response functions, which were estimated from complex frequency response functions, is proposed. The complex frequency response functions were obtained from the experimental data of the structure. The nonproportional damping matrix was identified through the proposed method. Two numerical examples (lumped-mass model and cantilever beam model) were considered to verify the performance of the proposed method. As a result, the damping matrix of the nonproportional system was accurately identified.

Keywords:

Damping matrix identification, Complex frequency response function, Normal frequency response function

키워드:

감쇠행렬 추정, 복소 주파수 응답함수, 정상상태 주파수 응답함수

1. 서 론

현재 해양구조물, 선박, 잠수함 등의 고성능, 대형 구조물의 진동을 줄이기 위하여 감쇠 성능을 향상 시킨 감쇠복합재가 널리 사용되고 있다. 감쇠구조물의 해석을 위해서는 정확한 감쇠모델을 구성하는 것이 중요하지만, 감쇠특성을 모델링 하는 것은 매우 어려운 일이다. 부정확한 감쇠 모델링에서 기인하는 오차는 진동 소음 문제 및 구조물 안전 평가 등에 많은 어려움을 주고 있다. 이러한 이유로 국내/외에서 감쇠행렬을 추정하는 기법의 연구가 많이 진행되고 있다.

감쇠행렬 추정방법은 데이터 이용방법에 따라 크게 간접방법(Indirect method)과 직접방법(Direct method)으로 나누어진다. 간접방법은 진동 데이터에서 고유진동수, 감쇠비, 모드형상과 같은 모드 특성치(Modal parameter)를 추정하여 수치모델(대부분의 경우 유한요소 모델)의 행렬을 수정하는 방식으로 감쇠행렬을 추정하는 방법이다. Lee et al. [1]은 유한요소 모델 개선기법(Finite element model updating)을 이용한 비례 감쇠행렬과 비비례 감쇠행렬을 추정기법을 연구하였다. Park et al. [2]은 유전알고리즘을 이용한 감쇠행렬 산출법에 대하여 연구를 수행하였으며, Min et al. [3]은 유한요소 모델 개선기법을 이용한 비비례 감쇠행렬 추정기법을 발표하였다. 간접방법의 경우 감쇠행렬의 정확한 추정을 위해서는 모델의 질량행렬과 강성행렬이 정확히 추정되어야 하는 어려움이 있다.

반면에 직접방법은 모델을 이용하지 않고 획득된 진동 데이터로부터 감쇠행렬을 바로 추정하는 방법이다. 감쇠행렬 추정을 위한 직접방법 연구로써 Lee and Kim [4], Kim et al. [5], Pradhan and Modak [6]은 정상상태 주파수 응답함수(Normal frequency response function)와 복소 주파수 응답함수(Complex frequency response function)의 관계를 이용한 감쇠행렬 추정 방법에 대하여 연구하였다. Min et al. [7]은 복소 고유주파수와 복소 모드형상을 이용하여 집중질량 모델에 적용 가능한 감쇠행렬 추정 기법을 연구하였다. Arora [8]은 정상상태 주파수 응답함수를 이용하여 구조 감쇠행렬을 추정하는 연구를 발표하였다.

본 연구에서는, Arora [8]에서 제안한 구조 감쇠행렬 추정기법을 수정하여 비비례 점성감쇠행렬을 추정하는 기법을 제안하고, 두 가지(3자유도 집중질량 모델과 외팔보 모델) 수치모델을 이용하여 제안된 기법의 정확도를 검토하였다.

2. 감쇠행렬 추정

2.1 주파수 응답 데이터를 이용한 감쇠행렬 추정

n 자유도 점성감쇠 시스템의 운동방정식은 아래와 같다.

M x ̈ t C + C x ̇ t C + K x t C = f t

(1)

여기서, M은 질량행렬, C는 감쇠행렬, K는 강성행렬이며, x(t)와 f(t)는 시간에 따른 변위 벡터와 힘 벡터이다. 위첨자 ‘C’는 감쇠시스템을 의미한다. 조화가진, f(t)=F(ω^jwt),으로 가정하면 식 (1)은 아래와 같이 정리된다.

K - ω 2 M X ω C + jωCX ω C = F ω

(2)

여기서, x(t)^C=X(ω)^Ce^jwt이며 j는 허수를 나타낸다. 식 (2)에서 K-ω²M은 아래와 같이 표현될 수 있다.

Z ω N = K - ω 2 M = α ω N - 1

(3)

여기서, α(ω)^N은 실수 혹은 정상상태 주파수 응답함수을 나타내며, 위첨자 ‘N’은 실수 혹은 정상상태를 의미한다. 식 (3)을 식 (2)에 대입하고, 양변에 [α(ω)^N]를 곱하여 식 (4)를 얻을 수 있으며, 그 후 식 (5) 변환행렬[9]를 식 (4)에 대입하여 정리하면 식 (6)을 얻을 수 있다.

X ω C + jωα ω N CX ω C = α ω N F ω

(4)

G ω = ω α ω N C

(5)

I + jG ω X ω C = α ω N F ω

(6)

식 (6)에서 변위 벡터, X(ω)^C,는 힘 벡터와 복소 주파수 응답함수의 곱으로 표시될 수 있다.

X ω C = α ω C F ω = α ω R C + jα ω I C F ω

(7)

식 (7)을 이용하면, 식 (6)은 아래와 같이 정리된다.

I + jG ω α ω R C + jα ω I C = α ω N

(8)

식 (8)을 실수부와 허수부로 정리하면

α ω R C - G ω α ω I C + j G ω α ω R C + α ω I C = α ω N

(9)

정상상태 주파수 응답함수의 경우 허수부는 0이 되어야 하므로,

G ω = - α ω I C α ω R C - 1 = ωα ω N C

(10)

식 (10)을 감쇠행렬로 정리하면,

C = - 1 ω α ω N - 1 α ω I C α ω R C - 1

(11)

식 (11)은 감쇠행렬을 구하기 위한 기본식이 되며, 정상상태 주파수 응답함수와 복소 주파수 응답함수의 관계는 다음과 같다.

α ω N = α ω R C + α ω I C α ω R C - 1 α ω I C

(12)

측정을 통해 m개의 복소 주파수 응답데이터를 획득할 경우 식 (11)은 아래와 같이 정리될 수 있다.

C n × n = ω 1 α ω 1 N ω 1 α ω 1 N ⋮ ω m α ω m N n × m + - α ω 1 I C α ω 1 R C - 1 - α ω 2 I C α ω 2 R C - 1 ⋮ - α ω m I C α ω m R C - 1 m × n

(13)

여기서, 위첨자 ‘+’는 유사역행렬(Pseudo inverse matrix)을 의미한다. 정리하면, 측정을 통해 m개의 복소 주파수 응답데이터를 n개의 자유도에서 획득할 경우 식 (13)을 이용하여 [n×n] 크기의 감쇠행렬을 추정할 있다.

2.2 3자유도 비비례 점성감쇠 시스템

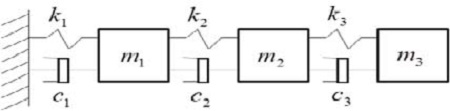
제안된 기법을 검증하기 위하여 m₁,m₂,m₃는 10kg, 14kg, 12kg이며, k₁,k₂,k₃는 2000N/m, 3000N/m, 2500N/m이고, c₁,c₂,c₃는 2.1Ns/m, 3.2Ns/m, 2.5Ns/m인 3자유도 비비례 점성감쇠 시스템을 Figure 1과 같이 구성하였다. 이 시스템을 구성하는 M, C, K는 Table 1과 같다. 이 중 M과 K는 알고 있는 상태로 가정하였으며, C는 모르는 상태로 제안된 기법을 통해 추정하는 수치검증 시나리오를 고려하였다. 3자유도 수치모델로부터 9개의 복소 주파수 응답함수를 획득 하였으며, 이중 0 ~ 50Hz 범위에서 획득된 복소 주파수 응답함수 데이터만을 감쇠행렬 추정에 이용하였다.

Figure 1:

3-DOF nonproportional viscous damping system

Table 1:

System matrices of 3-DOF nonproportional viscous damping system

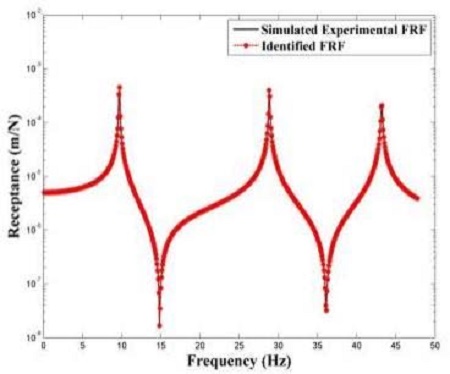
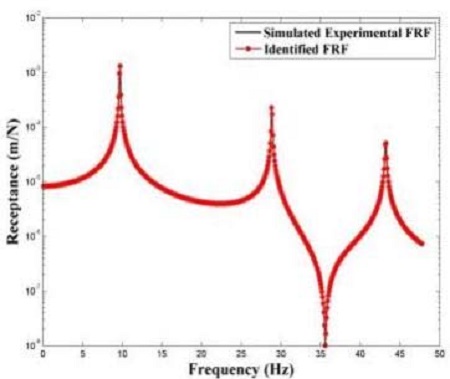
식 (13)을 통해 추정된 시스템의 복소 주파수 응답함수와 수치모델의 복소 주파수 응답함수를 비교하여 정확성을 검토하였다. Figure 2와 Figure 3은 추정된 모델과 수치모델의 복소 주파수 응답함수, FRF_1,1과 FRF_2,3 이다. FRF_i,k에서 i는 가진점 위치, k는 응답점 위치를 나타낸다. 검정색 실선은 수치모델의 복소 주파수 응답함수이며, 빨간색 점선은 추정된 시스템의 복소 주파수 응답함수로 두 선이 매우 잘 일치하는 것을 확인 할 수 있다. 추정된 감쇠행렬과 오차율을 Table 2에 정리하였다. Table 2로부터 추정된 감쇠행렬이 수치모델과 정확히 일치하는 것을 확인 할 수 있다.

Figure 2:

Overlay plot of simulated experimental FRF1,1 and identified FRF1,1

Figure 3:

Overlay plot of simulated experimental FRF2,3 and identified FRF2,3

Table 2:

Estimated damping matrix from FRFs without noise and absolute error

2.3 외팔보 유한요소 모델

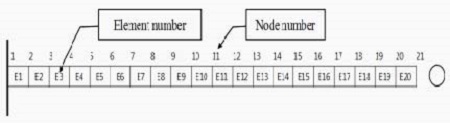
제안된 기제안된 감쇠행렬 추정기법을 검증하기 위하여 원형 외팔보 모델을 Figure 4와 같이 생성하였다. 수치해석 모델에 사용된 물성치와 수치는 Table 3과 같다. 총 20개의 요소와 21개의 절점으로 구성되었으며, 각 절점 당 2개의 자유도(회전과 병진 자유도)를 가지고 있다. 따라서 한쪽 고정조건을 고려하면 외팔보의 질량행렬과 강성행렬은 38×38의 크기를 가진다. 이러한 경우 식 (13)을 통해 감쇠행렬을 추정하기 위해서는 총 1444개의 복소 주파수 응답함수를 추정해야 하는 어려움이 있다. 또한 실제 실험모델의 자유도는 센서의 측정자유도와 사용된 개수의 곱으로 제한되기 때문에 자유도 축소가 고려되어야 한다. 이러한 자유도의 제한을 고려하기 위해 자유도 축소기법[10]을 사용하여 3, 5, 7, 9, 11, 13, 15, 17, 19, 21번 절점에서 각각 3, 7, 11, 15, 19, 23, 27, 31, 35, 39번의 병진자유도만을 가지는 10자유도 모델로 수치모델을 축소시켰으며, 축소된 모델과 축소 전 모델의 1 ~ 10차 고유주파수들의 차이가 0.05 %보다 작게 되도록 하였다. 축소된 질량행렬과 강성행렬을 각각 M_R과 K_R로 정의하였으며, 식 (14)를 이용하여 비비례 점성감쇠 행렬을 구성하였다.

Figure 4:

Finite element model of a cantilever beam

Table 3:

Properties of a FE model

C i, j = 10 - 6 × α i, j × K Ri, j, C i, j = C j, i

(14)

여기서, C_i,j와 K_Ri,j는 감쇠행렬과 강성행렬의 i번째 행과 j번째 열의 성분, α_i,j는 0 ~ 1사이의 불규칙 값이다. 생성된 비비례 감쇠행렬을 Table 4에 나타내었다.

Table 4:

Nonproportional damping matrix of numerical model

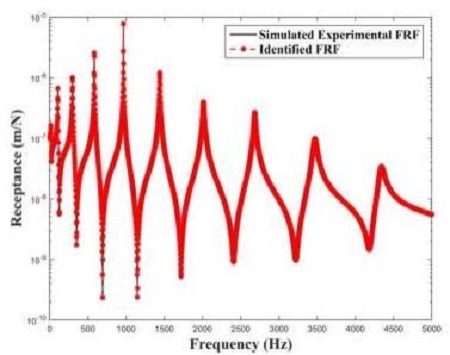
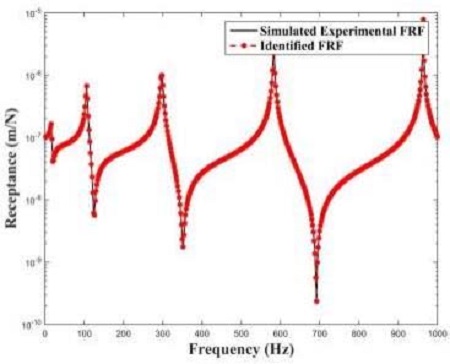
M_R, K_R, C로부터 100개의 복소 주파수 응답함수를 획득하였다. 이중 0 ~ 5000Hz 범위에서 획득된 복소 주파수 응답함수 데이터(Case 1)와 0 ~ 1000Hz범위에서 획득된 복소 주파수 응답함수 데이터(Case 2)를 각각 감쇠행렬 추정에 이용하였다. Case 1과 Case 2에서 추정된 모델과 수치모델의 복소 주파수 응답함수를 Figure 5와 Figure 6에서 비교하였다. Case 1과 Case 2 모두에서 추정된 모델의 복소 주파수 응답함수와 수치모델의 복소 주파수 응답함수가 매우 잘 일치하는 것을 확인 할 수 있다. 이 결과는 직접법이 가지고 있는 장점을 잘 보여준다. [n×n] 크기의 감쇠행렬을 추정하기 위해서 직접법은 [n×n×m] 크기의 복소 주파수 응답함수 행렬이 필요하고, 간접법의 경우 n개의 모드 특성치가 필요하다. 다시 정리하면, [n×n] 크기의 감쇠행렬을 추정하기 위해서 직접법의 경우 [n×n] 점에서 복소 주파수 응답함수를 계측하면 되기 때문에 간접법과는 다르게 자유도에 제한이 없다. 간접법의 경우 일반적으로 [n×n] 크기의 감쇠행렬을 추정하기 위해서는 n개의 고유주파수 혹은 고유모드 등을 추정하여야 하는 단점이 있다.

Figure 5:

Overlay plot of simulated experimental FRF1,1 and identified FRF1,1,, Case 1

Figure 6:

Overlay plot of simulated experimental FRF1,1 and identified FRF1,1,, Case 2

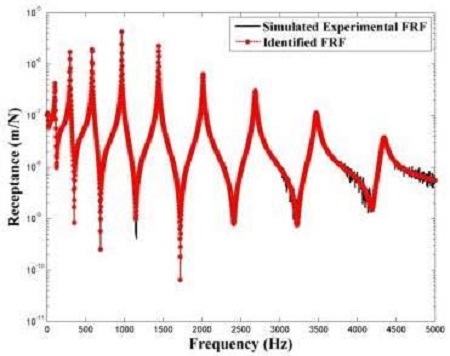
진동실험을 통해 실제 계측된 데이터에는 잡음이 필연적으로 포함되기 때문에 잡음에 대한 강건성(Robustness) 검토가 필요하다. 잡음에 대한 강건성 검토를 위해 Case 1의 복소 주파수 응답함수 데이터에 2%의 잡음을 인위적으로 추가하여(Case 3) 감쇠행렬 추정에 적용하였다. Figure 7은 Case 3에서 추정된 모델의 복소 주파수 응답함수와 수치모델의 복소 주파수 응답함수를 비교한 것으로 매우 잘 맞는 것으로 보인다. 그러나 Figure 7에서 보이는 것과는 달리 추정된 감쇠행렬(Table 5)은 수치모델의 감쇠행렬과 많은 차이를 보였는데, 이러한 오차는 복소 주파수 응답함수에 포함된 잡음에서 기인한 것으로 생각된다.

Figure 7:

Overlay plot of simulated experimental FRF1,1 and identified FRF1,1, Case 3

Table 5:

Identified nonproportional damping matrix, Case 3

3. 결 론

본 연구에서는 비비례 점성감쇠행렬 추정을 위해 복소 주파수 응답함수를 이용하는 직접추정 기법을 제안하였으며, 제안된 기법을 3자유도 집중질량 모델과 외팔보 수치 모델을 통해 성능을 검토하였다. 수치 모델을 이용한 성능검토를 통하여 다음과 같은 결론을 얻을 수 있었다.

(1) [n×n] 크기의 복소 주파수 응답함수를 계측할 수 있다면, [n×n] 크기의 비비례 점성감쇠행렬을 바로 추정할 수 있다. 이 경우 수치 모델이 필요 없기 때문에 모델 업데이트와 같은 추가적인 계산비용이 소모되지 않는다.

(2) 시험모델에 적용할 경우 자유도 축소기법을 연계하여 사용하면 효율적으로 비비례 점성감쇠행렬을 추정할 수 있다.

제한된 기법을 실제 구조물에 적용하기 위해서는 다음과 같은 사항들이 연구될 필요가 있다.

(1) 제안된 기법의 잡음에 대한 강건성 연구가 수행될 필요가 있다. 실제 계측된 데이터에는 필연적으로 잡음이 포함되기 때문에 잡음에 대한 강건성 확보가 필요한데, Case 3과 같이 잡음이 포함된 데이터를 이용할 경우 오차가 크게 나타나는 것이 확인 되었다.

(2) 보다 정확하고 효율적인 감쇠행렬 추정을 위해서는 추정에 사용되는 복소 주파수 응답함수의 범위 최적화 연구가 진행될 필요가 있다. 위의 사항들을 고려하여 실제 구조물에 적용 가능한 감쇠행렬 추정기법을 향후 개발하고자 한다.

Acknowledgments

본 연구는 선박해양플랜트연구소 주요사업으로 수행되고 있는 “해양플랜트 Topside 기자재 CAE 기술 개발”과제의 연구결과 중 일부임을 밝히며, 연구비 지원에 감사드립니다.

References

G. M. Lee, Y. H. Ju, and M. S. Park, “Comparison of damping matrix estimation methods for model updating”, Transactions of the Korean Society for Noise and Vibration Engineering, 20(10), p923-930, (2010), (in Korean). [https://doi.org/10.5050/KSNVE.2010.20.10.923]
S. C. Park, Y. B. Park, K. I. Park, H. K. Je, and G. J. Yi, “Identification of damping matrix for a steel bar by the genetic algorithm”, Journal of the Korean Society of Marine Engineering, 35(2), p271-277, (2011), (in Korean). [https://doi.org/10.5916/jkosme.2011.35.2.271]
C. H. Min, H. I. Park, and S. Y. Park, “Direct identification of non-proportional modal damping matrix for lumped mass system using modal parameters”, Journal of Mechanical Science and Technology, 26(4), p993-1002, (2012). [https://doi.org/10.1007/s12206-012-0221-1]
J. H. Lee, and J. Kim, “Development and validation of a new experimental method to identify damping matrices of a dynamic system”, Journal of Sound and Vibration, 246(3), p505-524, (2001). [https://doi.org/10.1006/jsvi.2001.3670]
K. S. Kim, Y. J. Kang, and J. Yoo, “Structural parameters identification using improved normal frequency response function method”, Mechanical Systems and Signal Processing, 22, p1858-1868, (2008). [https://doi.org/10.1016/j.ymssp.2008.02.001]
S. Pradhan, and S. V. Modak, “A method for damping matrix identification using frequency response data”, Mechanical Systems and Signal Processing, 33, p69-82, (2012). [https://doi.org/10.1016/j.ymssp.2012.07.002]
C. H. Min, H. W. Kim, C. H. Lee, S. Hong, J. S. Choi, and T. K. Yeu, “Identification of a nonproportional damping matrix using the finite element model updating”, Journal of Ocean Engineering and Technology, 26(4), p86-91, (2012), (in Korean). [https://doi.org/10.5574/KSOE.2012.26.4.086]
V. Arora, “Structural damping identification method using normal FRFs”, International Journal of Solids and Structures, 51, p133-143, (2014). [https://doi.org/10.1016/j.ijsolstr.2013.09.017]
S. Y. Chen, M. S. Ju, and Y. G. Tsuei, “Estimation of mass, stiffness and damping matrices from frequency response functions”, Journal of Vibration and Acoustics, 118(1), p78-82, (1996). [https://doi.org/10.1115/1.2889638]
M. I. Friswell, S. D. Garvey, and J. E. T. Penny, “Model reduction using dynamic and iterated IRS techniques”, Journal of Sound and Vibration, 186(2), p311-323, (1995). [https://doi.org/10.1006/jsvi.1995.0451]