투명 플렉시블 무선통신 소자구현을 위한 PES 박막상의 단파장 선로에 대한 고주파 특성연구


Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 소형화된 투명 플렉시블 무선통신소자 구현을 위해, 주기적 접지구조를 가지는 fishbone 형태의 전송선로를 PES (polyether sulfone) 박막상에 제작하였으며, 이에 관한 RF 특성을 고찰하였다. PES 상의 주기적 접지구조를 가지는 fishbone 형태의 전송선로는 종래의 전송선로에 비해 축소된 파장특성을 보여주었으며, 50 GHz의 주파수에서 선로파장은 1.91 mm으로, 종래의 코프레너 선로의 48.5%이다. 삽입손실 측정결과에 의하면 주기적 접지구조를 가지는 fishbone 형태의 전송선로는 40 GHz 까지의 주파수 범위에서 1.75 dB보다 낮은 저손실특성을 보여주었다. 대역폭 추출결과에 의하면, 주기적 접지구조를 가지는 fishbone 형태의 전송선로는 통과대역이 250 GHz인 광대역 특성을 보였다. 제안된 구조의 전송선로에 대한 특성임피던스 추출결과에 의하면, 제안된 구조의 전송선로는 종래의 주기적 선로구조에 비해 양호한 주파수 특성을 보여주었으며, 이로 인해 광대역의 전송선로 및 광대역 분포형 수동소자에 이용될 수 있음을 알 수 있었다. 그리고, 주기적 접지구조를 가지는 fishbone 형태의 전송선로는 종래의 전송선로에 비해 낮은 임피던스 특성을 보였으며, 이로 인해 좁은 선로폭으로 낮은 특성임피던스를 가지는 선로를 구현할 수 있었으며, 이는 RF 회로상의 점유면적을 줄이는데 크게 기여하였다.
Abstract
This work presents an investigation of the radio frequency characteristics of an FTLPGS (fishbone-type transmission line employing periodic ground structure) fabricated on PES (polyether sulfone) for the realization of a transparent flexible wireless communication device. According to the results, the FTLPGS on PES showed a shorter wavelength characteristic when compared with a conventional coplanar waveguide. Concretely, the wavelength of the FTLPGS was 1.91 mm at 50 GHz, which was 48.5% of the conventional coplanar waveguide. The bandwidth extraction result showed that the passband of the FTLPGS on PES was 250 GHz. Unlike conventional periodic structures, the characteristic impedance of the FTLPGS on PES also showed a very low frequency dependency. A miniaturization of the RF circuit on the PES substrate was made possible by the FTLPGS on PES having shown characteristic impedance lower than that of conventional transmission lines. These results mean that, with a broadband operation frequency, the FTLPGS on PES is a suitable construction application for the transmission line and distributed passive components.
Keywords:
Flexible wireless communication device, Polyether sulfone, Fishbone-type Transmission Line employing periodic ground strucurte, bandwidth키워드:
플렉시블 무선통신소자, PES (polyether sulfone), 주기적 접지구조를 가지는 fishbone 형태의 전송선로, 대역폭1. 서 론
최근 차세대 투명 플렉시블 디스플레이 응용을 위한 박막재료로서 PES (polyether sulfone)가 주목을 받고 있다 [1][2]. PES는 다른 투명박막재료에 비해 비교적 고온에서 소자공정이 가능하여, 양질의 전자소자를 제작할 수 있는 장점이 있다[3]-[6]. 이와 같은 PES의 장점으로 인해 최근에는 PES 박막이 RF 전자소자에 응용되고 있다[4]-[6]. 최근 보고에 의하면 PES의 RF 손실특성은 실리콘에 비해 훨씬 낮으며, 양호한 주파수 특성을 보여주었다[6]. 그러나, 저유전율을 가지는 PES는 실리콘보다 긴 파장특성을 보여주었으며, PES 박막상에 제작된 RF 소자의 점유면적이 매우 크다는 단점이 있었다[6]. 그 뿐 아니라, PES 박막상의 전송선로는 종래의 실리콘 박막상의 전송선로보다 훨씬 큰 특성임피던스 값을 보였다[6]. 구체적으로 두께 200 μm인 PES 박막상에 선로폭이 50 μm인 코프레너 선로가 제작되는 경우 100 Ω이상의 특성임피던스 값을 보였다. 이로 인해 저임피던스 소자간의 임피던스 정합을 위해서 매우 큰 선로 폭이 요구되었으며, 이는 PES 박막상의 RF 이러한 단점을 해결하기 위해 짧은 파장 특성을 가지는 fishbone 형태의 전송선로가 제안되었다[6]. fishbone 형태의 전송선로는 PES 박막상의 종래의 전송선로보다 높은 유효유전율 특성을 보여주었으며, 이로 인해 종래의 전송선로보다 단파장 특성을 보여주었다. 구체적으로 fishbone 형태의 전송선로의 파장은 종래의 전송선로의 파장의 55%임을 알 수 있었다[6]. 그뿐 아니라, 주기적인 용량의 증가로 fishbone 형태의 전송선로는 종로의 전송선로에 비해 비교적 낮은 특성 임피던스 값을 보여주었다.
최근, RF 소자의 사이즈를 더욱 축소하기 위해서 주기적 접지구조를 가지는 fishbone 형태의 전송선로가 제안되었다[4][5]. 그 결과에 의하면 주기적 접지구조를 가지는 fishbone 형태의 전송선로는 종래의 fishbone 형태의 전송선로에 비해 더욱 짧은 파장특성을 보여주었다[5]. 그러나, 플렉시블 무선통신소자에의 응용을 위해서는 다양한 사이즈를 가지는 선로구조에 대한 광범위한 RF 특성이 검토되어야 하나, 아직 이에 대한 검토가 이루어지질 못하였다.
본 논문에서는 주기적 접지구조를 구성하는 스트립의 길이를 변화시킴으로써, 스트립 길이변화에 따른 fishbone 형태의 전송선로의 RF 특성변화에 관한 연구를 수행하였다. 구체적으로, 다양한 길이의 주기적 접지스트립을 가지는 fishbone 형태의 전송선로에 대한 임피던스 및 대역폭 특성을 이론 및 실험적인 방법으로 구하였으며, 손실, 유효유전율 및 파장 등의 광범위한 고주파 특성에 대해 연구함으로써 고주파 통신소자로서의 응용가능성을 연구하였다.
2. Fishbone 형태의 전송선로의 구조 및 단파장특성
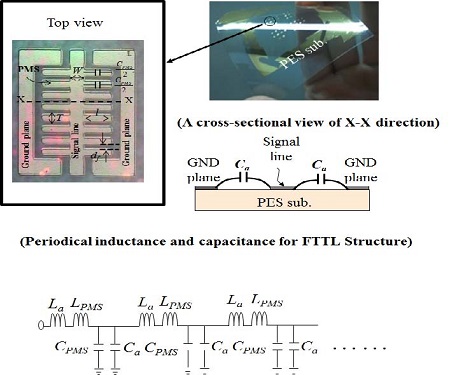
Figure 1은 PES 박막상에 제작된 종래의 fishbone 형태의 선로구조를 보여준다[6]. Fishbone 모양의 선로는 fishbone-type center line과 ground plane으로 이루어지며, fishbone-type center line은 signal line과 PMS’s (periodic metal strips)로 이루어진다. 종래의 코프레너 선로는 signal line과 ground plane 사이에 주기적인 용량 Ca만 존재하나, fishbone 모양의 선로는 Ca와 함께 주기적인 용량 CPMS도 존재한다. 이에 대한 원인은 PMS 자체가 각자 독립된 개방선로 형태이며, Figure 1과 같이 이러한 개방선로는 개방선로 용량 CPMS로 표현되기 때문이다. 다음의 식과 같이 전송선로의 파장과 특성임피던스는 주기적인 용량에 반비례하며, 이로 인해, fishbone 모양의 선로는 기존의 코프레너 선로에 비해 짧은 파장 특성과 낮은 임피던스 특성을 보이게 된다.
| (1) |
| (2) |
상기 식에서, ω, L과 C는 각각 각주파수, 전송선로의 단위길이당 인덕턴스와 단위길이당 정전용량값이다. 구체적으로 fishbone 형태의 전송선로의 파장은 종래의 전송선로의 파장의 55%임을 알 수 있었다[6]. 이와 같이 fishbone 모양의 선로구조는 종래의 코프레너 선로에 비해 낮은 임피던스와 짧은 파장특성을 보여주었으나, RF 회로의 응용을 위해서는 더 낮은 임피던스 값과 더 짧은 파장이 요구되었다. 구체적으로, 특성임피던스 값은 70 Ω이상으로 50 Ω의 기본 포트 임피던스를 가지는 마이크로파 회로에 응용하기에는 여전히 높은 임피던스 값을 보였으며, PES 박막상의 회로면적의 축소를 위해서는 더욱 짧은 파장이 요구되었다 [6].
식 (1), (2)로부터, 선로파장과 특성임피던스를 줄이기 위해서는 주기적인 용량값이 증가되어야 함을 알 수 있으며, 본 연구그룹에서는 이점에 착안하여 fishbone 형태의 전송선로 양측에 주기적인 접지구조를 배치한 선로구조를 제안하였으며[4][5], 선로구조는 Figure 2에 나타나있다. 플렉시블 무선통신소자에의 응용을 위해서는, 다양한 사이즈를 가지는 상기선로구조에 대해 광범위한 RF 특성이 검토되어야 하나, 아직 이에 대한 검토가 이루어지질 못하였다. 본 논문에서는 다양한 사이즈를 가지는 상기 선로구조에 대한 광범위한 RF 특성연구가 이루어졌다. 실지 상기 선로구조는 PCB 기판상에 제작된 적이 있으나 PCB 기판상에서는 협대역 특성에 의해 넓은 주파수 대역에서는 사용되지 못하였다[7]. 본 논문에서는 PES 박막상에 제작하여 넓은 주파수대역에서 응용하고자 한다.
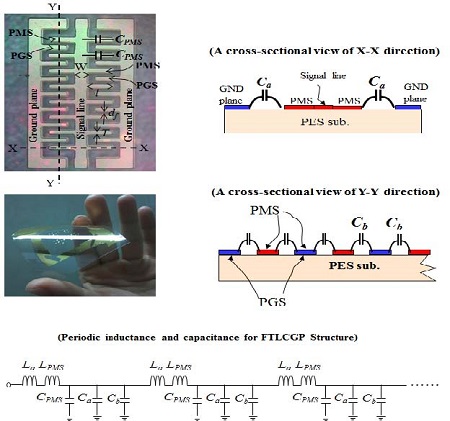
Structure of FTLPGS (fishibone-type transmission line employing periodic ground structure) on PES substrate [4][5]
Figure 2에서 보는바와 같이, 제안된 선로구조는 fishbone 형태의 선로부분과 주기적 접지구조로 이루어진다. fishbone 형태의 선로부분은 다시 signal line과 PMS’s (periodic metal strips)로 구성된다. 그리고, 주기적인 접지구조는 ground plane과 PGS’s (periodic ground strips)로 구성된다. PMS와 PGS는 교대로 배치되어 있다. 따라서, Figure 1의 종래의 fishbone 형태의 전송선로에 비해, Fig. 2의 선로구조는 PMS와 PGS 사이의 커플링에 의해 추가적인 용량 Cb를 가지며, 이로 인해 Figure 2의 선로구조는 종래의 전송선로에 비해 더 큰 주기적인 용량 값을 가지게 된다. 구체적으로 Figure 1의 종래의 fishbone 형태의 전송선로의 주기적 용량 값은 식 (3)과 같으며, Figure 2의 선로구조에 대한 주기적인 용량 값은 식 (4)와 같다.
| (3) |
| (4) |
Figure 1의 종래의 fishbone 형태의 전송선로의 경우에도, PMS사이에 커플링이 존재한다. 그러나, 식 (1), (2)에서의 용량 값 C는 선로와 접지사이에 존재하는 용량이므로, PMS사이에 커플링에 의한 용량은 파장축소에 기여하지 못한다.
PES 박막상에 제작된 기존의 코프레너 선로와 fishbone 모양의 전송선로에 대한 단위 길이당 용량비교를 위해 단위길이당 용량을 구하였다. 식 (1), (2)로부터 단위길이당 용량 C는 다음의 식으로 표현될 수 있다.
| (5) |
Table 1은 식 (5)로부터 추출된 PMS 길이 l = 160 μm인 주기적 접지구조를 가지는 fishbone 형태의 선로구조에 대한 단위 길이당 주기적 용량을 나타낸다. 비교를 위해 종래의 fishbone 형태의 선로구조와 종래의 코프레너 선로에 대한 주기적 용량 값도 제시하였다. 주기적 구조를 가지는 fishbone 형태의 선로구조를 제작하기 위해서 200 μm 두께의 PES상에 두께 2 μm의 Au/Ti 금속층이 증착되었다. Signal line과 ground plane의 폭은 각각 70과 120 μm이다. 그리고, 주기적인 PMS와 PGS의 길이와 폭은 각각 160과 30μm이며, PMS와 PGS 사이의 거리는 30μm이다. Table 1에서 보는 바와 같이 주기적인 접지구조를 가지는 fishbone 형태의 선로구조는 종래의 fishbone 형태의 전송선로와 코프레너 선로보다 훨씬 큰 주기적 용량을 보여준다.

Measured periodic capacitance of the FTLPGS (fishbone-type transmission line employing periodic ground structure) and conventional transmission lines on PES
Table 2는 PMS 길이 l = 160 μm인 주기적 접지구조를 가지는 fishbone 형태의 선로구조에 대한 파장측정결과를 나타낸다. 비교를 위해 종래의 fishbone 형태의 선로구조와 종래의 코프레너 선로에 대한 파장 값도 제시하였다. Table 2에서 보는 바와 같이 주기적 접지구조를 가지는 fishbone 형태의 선로구조 (Figure 2 참조)는 종래의 fishbone 형태의 전송선로 (Figure 1 참조)와 코프레너 선로에 비해 단파장특성을 보여주며, 이에 대한 원인은 단위 길이당 주기적 용량이 증가하였기 때문이다.

Measured wavelength of the FTLPGS (fishbone-type transmission line employing periodic ground structure) and conventional transmission lines on PES
상기 결과로부터 주기적인 접지구조를 가지는fishbone 모양의 전송선로를 이용하여 RF용 수동소자를 구현하면 기존의 선로구조를 이용하는 것 보다 점유면적이 훨씬 적음을 알 수 있다. 보다 자세한 내용은 뒷장에서 고찰하고자 한다.
3. 주기적 접지구조를 가지는 fishbone 형태의 전송선로에 대한 RF 특성
Table 3은 PES 박막상에서 주기적 접지구조를 가지는 길이 λ/4의 fishbone 모양의 선로구조에 대한 손실측정 결과를 보여준다. 참고로 PES 박막상의 종래의 코프레너 선로와 종래의 fishbone 형태의 전송선로의 손실특성도 추가되었다. 주기적 접지구조를 가지는 fishbone 모양의 선로구조는 기존의 코프레너 선로에 필적하는 저손실 특성을 나타내며, 구체적으로 40 GHz 까지의 주파수 범위에서 1.75 dB보다 낮은 손실특성을 보여주고 있다.
Table 2에서 설명한 바와 같이 주기적 접지구조를 가지는 fishbone 형태의 선로구조는 종래의 전송선로보다 높은 용량성분을 가지므로 축소된 길이의 파장을 가진다. 본 논문에서는 다양한 PMS의 길이 l에 대한 선로파장 측정결과도 제시하였다. Figure 3은 다양한 길이 l을 가지는 선로구조에 대한 파장특성을 보여준다. Figure 3에서 l = 0는 주기적 구조가 없는 전송선로에 해당한다. 그림에서 l = 0 ∼ 240 μm의 범위에서 l 이 증가할수록 파장이 짧아지며, 이에 대한 원인은 l이 증가할수록 용량 CPMS값과 Cb값이 커지기 때문이다. 즉, 주기적 접지구조를 가지는 fishbone 형태의 선로구조에 대한 단위길이당 용량 값은 식 (4)와 같으며, 식 (4)에서 CPMS값과 Cb값은 다음과 같이 표현된다.
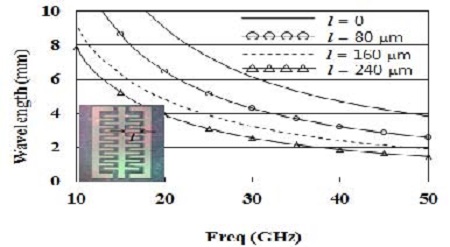
Measured wavelength of the FTLPGS (fishbone-type transmission line employing periodic ground structure) on PES
| (6a) |
| (6b) |
상기식에서 βl과 ω는 선로 폭 T와 길이 l을 가지는 PMS에 해당하는 전송상수와 각주파수이며, Zol은 선로 폭 T와 길이 l을 가지는 PMS 개별 선로에 해당하는 특성임피던스이다. 그리고, εeff는 유효유전율이며, th와 df는 각각 메탈두께와 PMS와 PGS 사이의 거리이다. CPMS값을 구하기 위해 개방선로 용량 식[8]을 적용하였으며, Cb값을 구하기 위해서 평판 커패시터 용량식을 적용하였다. βll < π/2인 범위에서 길이 l이 증가할수록 CPMS와 Cb값이 증가하여 식 (4)의 주기적인 용량 값이 증가됨을 알 수 있으며, 식 (1)로부터 선로의 용량 값이 커지면 파장이 짧아짐을 알 수 있다. Figure 4는 PMS의 길이 l의 변화에 따른 주기적인 용량 측정결과이다.
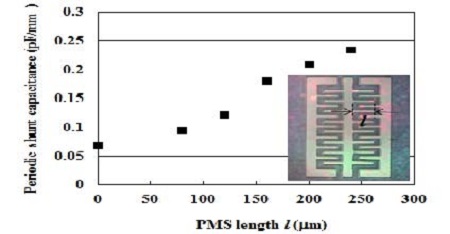
Measured periodic shunt capacitance of the FTLPGS (fishbone-type transmission line employing periodic ground structure) on PES
상기 결과로부터 주기적 접지구조를 가지는 fishbone 모양의 전송선로를 이용하여 고주파소자를 구현하면 기존의 전송선로를 이용하는 것 보다 소자면적이 훨씬 적어짐을 알 수 있다. 예를 들어 PMS의 길이가 160 μm인 주기적 접지구조를 가지는 fishbone 모양의 선로구조를 이용하여 PES 박막상에 특성임피던스 Z0가 59Ω인 λ/4 길이의 선로를 제작하면, 중심주파수 22 GHz에서 선로의 길이는 1 mm가 되어, PES상의 선로면적은 0.45 mm2가 된다. 그러나 PES 박막상에 특성임피던스 Z0가 59Ω이며 기존의 코프레너 선로로 이루어진 λ/4 선로를 제작하는 경우, 중심주파수 22 GHz에서 선로의 길이와 넓이는 각각 0.34과 2.3 mm가 되며, 선로면적은 0.782 mm2가 된다. 따라서, 주기적 접지구조를 가지는 fishbone 모양의 전송선로를 이용하여 고주파소자를 제작하면 기존의 코프레너 선로를 이용하는 것 보다 선로면적이 57.5%로 감소하게 된다.
Figure 5는 PMS의 길이 l의 변화에 따른 전송상수 측정결과이다. l = 0 ∼ 240 μm의 범위에서 l 이 커질수록 전송상수가 증가하며, 이에대한 원인은 l이 커질수록 용량 CPMS와 Cb값이 증가하여 slow-wave 특성이 더욱 강해지기 때문이다. 다음의 식으로부터 선로의 용량 값이 증가하면 전송상수 값이 커짐을 알 수 있다.
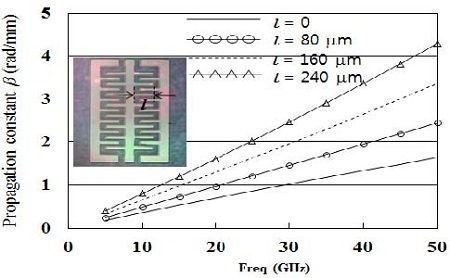
Measured propagation constant of the FTLPGS (fishbone-type transmission line employing periodic ground structure) on PES substrate
| (7) |
Figure 6은 PMS의 길이 l의 변화에 따른 주기적인 유효유전율 측정결과이다. 길이 l = 0 ∼ 240 μm의 범위에서 l 이 커질수록 유효유전율 값이 증가하며, 이에 대한 원인은 l이 커질수록 용량 CPMS와 Cb값이 증가하기 때문이다. 다음 식 으로부터 선로의 용량 값이 증가하면 유효유전율 값이 커짐을 알 수 있다.
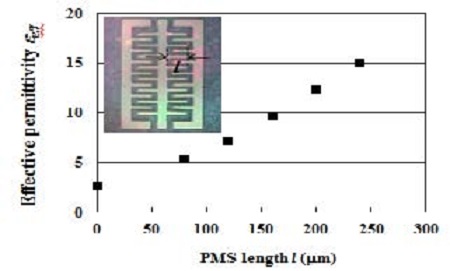
Measured effective permittivity εeff of FTLPGS (fishbone-type transmission line employing periodic ground structure) on PES substrate
| (8) |
상기 식에서 μ0와 ε0는 각각 공기의 투자율과 유전율이다.
4. 이론적 해석을 통한 주기적 접지구조를 가지는 fishbone 모양의 선로구조에 대한 특성 임피던스 및 대역폭 추출
일반적으로 수백 GHz에 이르는 높은 주파수의 신호의 대역특성을 실험적으로 측정하는 것은 어려우며, 선로의 대역폭을 추출하기 위해서는 이론적인 방법을 이용해야 한다. 본 논문에서는 주기적인 등가회로[8]를 사용하여 특성 임피던스 및 대역폭을 추출하였다. 임피던스 및 대역폭을 계산하기 위해서는 등가회로가 이용되어야 한다. Figure 7에서 fishbone 모양의 전송선로는, 용량 CPMS와 Cb가 종단 된 길이 d 인 주기적 전송선로구조로 나타내었다. 길이 d 는 주기적 구조에서 1개의 cell의 길이이며, Figure 2로부터 d 는 다음과 같이 표현된다.
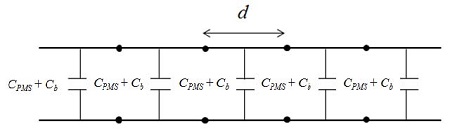
Equivalent circuit of the FTLPGS (fishbone-type transmission line employing periodic ground structure) structure with periodically loaded capacitance
| (9) |
상기 식에서 T와 df는 각각 PMS의 두께와 PMS와 PGS사이의 거리이다. Figure 2에서 보이는 주기적 접지구조를 가지는 fishbone 형태의 선로구조는 용량 Ca, CPMS와 Cb를 가지지만, 용량 Ca는 signal line과 ground plane사이의 용량이며, 길이 d인 주기적인 전송선로에 포함되어 있다. 주기적 접지구조를 가지는 FTLPGS 구조에서 주기적으로 존재하는 PMS의 개방선로 용량 CPMS와 Cb는 주기적인 세셉턴스 jb로 나타낼 수 있으며, 다음과 같다.
| (10) |
| (11) |
상기 식에서 ω는 각주파수 2πf이며, Z0는 PMS가 존재하지 않는 기존 코프레너 선로의 특성임피던스이다. Figure 8은 fishbone 모양의 전송선로에 대한 등가회로에 존재하는 전압 전류이다. 주기적 구조의 n번째 단위셀에 대한 입력 및 출력 전류 In,In+1과 입력 및 출력 전압 Vn,Vn+1은 ABCD 행렬에 의해 다음의 수식으로 나타내어 질 수 있다.
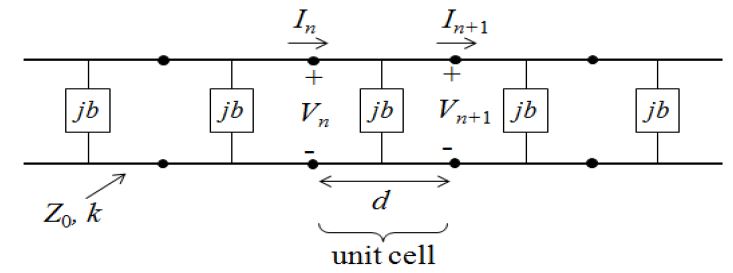
Voltage and current on the equivalent circuit of the FTLPGS (fishbone-type transmission line employing periodic ground structure) structure
| (12) |
| (13) |
| (14) |
상기 식 에서 μ0,ε0와 εe는 각각 공기에 대한 투자율, 유전율 및 주기적인 PMS가 존재하지 않는 종래의 코프레너 선로에 대한유효유전율이다. 주기적 구조를 가지는 선로의 전송상수를 ϒ라고 가정하면 다음 식이 만족된다[8].
| (15) |
| (16) |
| (17) |
근이 존재하기 위해 손실이 없는 회로에서 AD-BC = 1 임을 적용하면,
| (18) |
주기적 구조를 가지는 선로의 전송 상수 ϒ는 손실성분을 가지며, 따라서, ϒ = α + β가 되어, 아래의 식이 만족된다.
| (19) |
윗 식을 이용하여 α = 0, β ≠ 0일 때의 통과대역을 추출 할 수 있으며, α ≠ 0, β = 0일 때의 저지대역을 추출 할 수 있다. 통과대역과 저지대역을 추출하는 수식은 다음의 식으로 표현된다.
| (20) |
| (21) |
| (22) |
상기 식에서 통과대역의 전송상수 β값은 다음과 같이 나타내어 진다.
| (23) |
상기 식의 신뢰도를 확인하기 위해 식 (23)을 사용하여 추출된 전송상수 β값과 측정값을 비교하였다. Figure 9는 전송상수 β에 대한 계산결과와 측정결과를 나타낸다. 상기 식을 이용한 계산값이 측정값이 비슷한 결과를 보여줌을 알 수 있다.
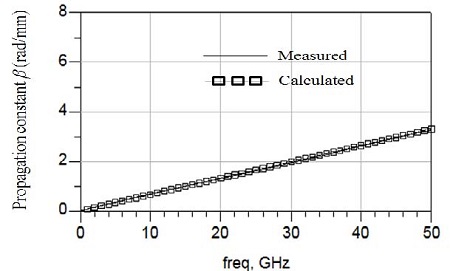
Measured and calculated propagation constant of FTLPGS (fishbone-type transmission line employing periodic ground structure) on PES substrate (l = 160 μm).
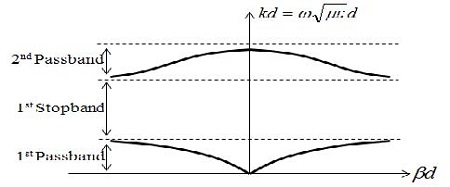
Figure 10은 상기 식 (20) ~ (22)를 이용하여 계산된 통과 및 저지대역에 대한 k-β 관계그래프이다. 다양한 l값을 가지는 fishbone 모양의 전송선로에 대한 대역폭 추출결과는 Table 4에 나타나 있다. 전송선로의 응용을 위해 사용하는 대역폭은 1차 통과대역이다. 대역폭 추출결과에 의하면 주기적 접지구조를 가지는 fishbone 모양의 전송선로는 PMS의 길이 l = 0 ∼ 240 μm의 범위에서 250 GHz까지는 전송선로로서 활용이 가능하다. PMS의 길이 l이 커질수록 1차 통과대역 대역폭이 좁아지며, 이에 대한 원인은 Figure 4에서 나타난 바와 같이 l 이 커질수록 병렬용량 값이 커지기 때문이다. 즉, Figure 2와 같이 주기적 접지구조를 가지는 fishbone 형태의 선로구조는 주기적인 커패시터와인덕터로 이루어진 저역통과 필터와 등가이며, 저역통과 필터의 차단주파수는 다음과 같다.

Calculated pass - and stopband of the TLPGS (fishbone-type transmission line employing periodic ground structure) structure.
| (24) |
상기 식에서 CPMS와 Cb값이 커지면 대역폭에 해당되는 차단주파수 fC값은 적어진다.
주기적 접지구조를 가지는 fishbone 모양의 전송선로의 특성 임피던스를 구하기 위한 특성 임피던스의 식은 다음과 같다.
| (25) |
| (26) |
| (27) |
| (28) |
A = D라는 점을 이용하며 특성 임피던스 수식을 구하면 아래의 식을 얻을 수 있다.
| (29) |
Figure 11은 PMS 길이 l값의 변화에 따른 특성 임피던스 추출결과를 보여준다. 같이 l 이 커질수록 특성임피던스가 적어지며, 이에 대한 원인은 l이 커질수록 용량 CPMS와 Cb값이 증가하기 때문이다. 즉, 병렬커패시턴스의 용량 Ct값은 식 (4), (6a), (6b)와 같이 나타내어지며, 특성임피던스 식은 식 (2)로부터 아래와 같이 나타내어진다.
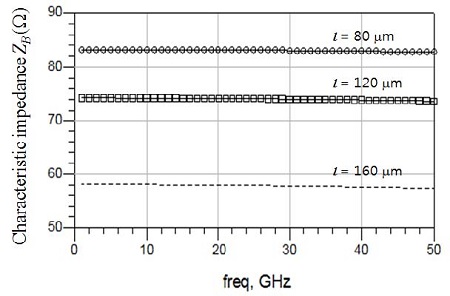
The dependency of characteristic impedance of FTLPGS (fishbone-type transmission line employing periodic ground structure) on frequency
| (30) |
식 (6a), (6b)와 (30)을 참고하면 βll < π/2인 범위내에서 l 이 커질수록 CPMS와 Cb값이 커지게 되며, 이로인해 특성임피던스 ZB값은 줄어들게 된다. 그러므로, PMS 길이 l값을 조정하면 주기적 접지구조를 가지는 fishbone 모양의 전송선로에 대한 특성임피던스 ZB값을 조정할 수 있다. 따라서, 제안된 선로구조를 이용하면 다양한 임피던스 값을 가지는 fishbone 모양의 전송선로를 용이하게 제작할 수 있다. 주기적 접지구조를 가지는 fishbone 모양의 전송선로에 대한 임피던스의 주파수 의존성은 매우 적음을 알 수 있다. 기존의 주기적 구조[9]-[13]의 경우, 특성 임피던스 주파수 의존성이 매우 커서, 전송선로에는 사용되지 못하였다. 그러나 본 논문에서 제안된 구조는 특성 임피던스의 주파수 의존성이 매우 적으므로 광대역 특성을 가지는 고주파소자에 사용될 수 있다.
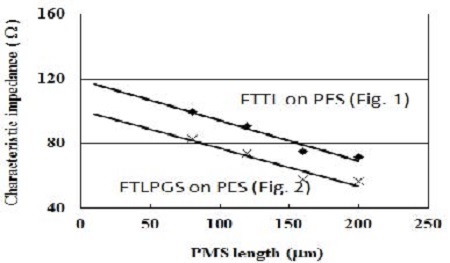
PES 박막상의 전송선로는 종래의 실리콘 박막상의 전송선로보다 훨씬 큰 특성임피던스 값을 보였다[6]. 구체적으로 두께 200 μm인 PES 박막상에 선로폭이 50 μm인 코프레너 선로가 제작되는 경우 100 Ω이상의 특성임피던스 값을 보였으며, 종래의 fishbone 형태의 선로구조의 경우, 70 Ω이상의 특성임피던스 값을 보였다. 이로 인해 PES 박막상에 특성임피던스 값이 50 Ω인 선로를 구현하는 것이 불가능하였으며, 저임피던스 소자간의 임피던스 정합을 위해서 매우 큰 선로 폭이 요구되었다[6]. 그러나, 주기적 접지구조를 가지는 fishbone 형태의 선로구조를 이용하면 적은 선로 폭으로 저임피던스 선로를 구현할 수 있으며, 특성임피던스 값이 50 Ω인 선로의 구현이 가능하다. Figure 12는 종래의 fishbone 형태의 선로구조와 주기적 접지구조를 가지는 fishbone 형태의 선로구조에 대한 특성임피던스 값을 보여준다. 그림에서 보는 바와 같이 주기적 접지구조를 가지는 fishbone 형태의 선로구조 (Figure 2 참조)는 종래의 fishbone 형태의 선로구조 (Figure 1 참조)보다 낮은 임피던스 특성을 보여준다. 이에 대한 이유는 Figure 2에서 보는 바와 같이, PMS와 PGS사이의 coupling 용량 값 Cb에 의해, 주기적 접지구조를 가지는 fishbone 형태의 선로구조 (Figure 2)가 종래의 fishbone 형태의 선로구조 (Figure 1)보다 더 큰 용량 값을 보이기 때문이다. 용량 값은 Table 1에 나타나 있다. 즉, 식 (2)에서와 같이, 주기적 용량 값이 클수록 더 낮은 특성 임피던스 값을 보임을 알 수 있다. 이러한 결과는 RF 회로상의 면적을 줄이는데 있어서 매우 유리하게 작용한다. 구체적으로, Figure 12에서 보는 바와 같이 PES 박막상에 특성임피던스 값이 75 Ω인 선로를 구현하는 경우, 종래의 fishbone 형태의 선로구조 (Figure 1)에 대한 PMS의 길이는 160 μm이며, PMS를 포함한 전체 선로폭은 390 μm이다. 반면, 주기적 접지구조를 가지는 fishbone 형태의 선로구조 (Figure 2)에 대한 PMS의 길이는 120 μm이며, PMS를 포함한 전체선로폭은 310 μm이다. 그리고, Figure 12에서 보는 바와 같이, 종래의 fishbone 형태의 선로구조 (Figure 1)를 이용하면 특성임피던스 값이 50 Ω인 선로의 구현이 불가능하다. PES 박막상에 제작된 종래의 fishbone 형태의 선로구조의 고임피던스 특성때문에, 기본 임피던스가 50 Ω으로 이루어진 마이크로파 회로망에 정합소자로서 이용하는 것이 불가능하였다[6]. 그러나, Figure 12에서 보는 바와 같이 PMS의 길이가 200 μm이상인 주기적 접지구조를 가지는 fishbone 형태의 선로구조 (Figure 2)를 이용하면, 특성임피던스 값이 50 Ω인 선로의 구현이 가능함을 알 수 있었다.
5. 결 론
본 연구에서는 주기적 접지구조를 가지는 fishbone 모양의 전송선로를 PES 박막상에 구현하였으며 상기 선로에 대한 고주파 특성을 연구하였다. 그 결과에 의하면 PES 박막상에 구현된 주기적 접지구조를 가지는 fishbone 모양의 선로구조는 기존의 코프레너선로보다 훨씬 짧은 파장특성을 보여주었다. 구체적으로 종래의 코프레너 선로와 종래의 fishbone 형태의 전송선로의 파장은 50 GHz에서 각각 3.94 mm와 2.23mm이나, 주기적 접지구조를 가지는 fishbone 형태의 전송선로의 파장은 1.91 mm로, 종래의 코프레너 선로의 48.5%이며, 종래의 fishbone 형태의 전송선로의 85.7%이다. 따라서, 상기 주기적 접지구조를 가지는 fishbone 모양의 선로를 사용하면 소형의 고주파소자를 제작할 수 있다. 예를 들어 PMS의 길이가 160 μm인 주기적 접지구조를 가지는 fishbone 모양의 선로구조를 이용하여 PES 박막상에 특성임피던스 Z0가 59Ω인 λ/4 길이의 선로를 제작하면, 중심주파수 22 GHz에서 선로의 길이는 1 mm가 되어, PES상의 선로면적은 0.45 mm2가 되어, 이는 종래의 코프레너 선로에 비해 면적이 57.5%이다. 그리고, PMS의 길이 l = 0 ∼ 240 μm의 범위에서, l 이 커질수록 파장은 줄어들고, 전송상수와 유효유전율은 커지는데, 이에 대한 원인은 l이 커질수록 주기적인 용량 CPMS와 Cb값이 증가하기 때문이다. 삽입손실 측정결과에 의하면 주기적 접지구조를 가지는 fishbone 형태의 전송선로는 종래의 코프레너 선로에 필적하는 양호한 손실 특성이 관찰되었으며, 구체적으로 λ/4 전송선로의 경우 40 GHz 까지의 주파수 범위에서 1.75 dB보다 적은 손실특성을 보여주었다. 본 논문에서는 등가회로를 사용하여, 이론적인 방법으로 주기적 접지구조를 가지는 fishbone 모양의 선로구조에 대한 특성 임피던스와 대역폭을 계산하였다. 사용한 이론식에 대한 신뢰도를 확인하기 위해 전송상수 β에 대한 측정결과와 계산결과를 비교하였으며, 그 결과가 일치함을 알 수 있었다. 계산결과에 의하면, PMS의 길이 l = 0 ∼ 240 μm의 범위에서 통과대역이 250 GHz인 광대역 특성을 보여주었다. 그리고, PMS의 길이 l이 커질수록 대역폭이 감소하였으며, 이에 대한 원인은 l이 커질수록 용량 CPMS와 Cb값이 증가하여 차단주파수가 감소하기 때문이었다. 특성 임피던스 계산결과를 통해, PMS 길이 l값을 조정하면 다양한 임피던스 값을 가지는 전송선로를 용이하게 제작할 수 있음을 확인하였다. 그리고 본 논문에서 제안하는 주기적 접지구조를 가지는 fishbone 모양의 전송선로의 특성임피던스는 종래의 전송선로에 비해 양호한 주파수 특성을 보여주었다. 따라서, 주기적 접지구조를 가지는 fishbone 모양의 전송선로는 광대역특성을 가지는 RF소자에 사용될 수 있음을 확인하였다. 그리고, 주기적 접지구조를 가지는 fishbone 형태의 전송선로는 종래의 fishbone 형태의 전송선로에 비해 낮은 임피던스 특성을 보여주었으며, 이로 인해 동일한 임피던스를 구현하기 위해 훨씬 더 적은 선로 폭이 요구되었다. 그리고, PES 박막상의 종래의 전송선로구조의 경우 고임피던스 특성 때문에 특성임피던스 값이 50 Ω인 선로의 구현이 어려웠으나, 주기적 접지구조를 가지는 fishbone 형태의 전송선로를 이용하면 특성임피던스 값이 50 Ω인 선로를 쉽게 구현할 수 있었다.
Acknowledgments
본 논문은 LG연암문화재단의 교수해외연구지원에 의하여 수행되었음. 이 논문은 2014년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(2014R1A2A1A11049844).
References
-
M. S. Oh, D. K. Hwang, K. M. Lee, S. Im, and S. Yi, “Low voltage complementary thin-film transistor inverters with pentacene-ZnO hybrid channels on AlOXdielectric”, Applied Physics Letters, 90(17), p173511-1-3, (2007).
[https://doi.org/10.1063/1.2732819]

-
Y. W. Choi, I. D. Kim, H. L. Tuller, and A. I. Akinwande, “Low-voltage Oganic Transistors and Depeletion-Load Inverters With High-K Pyrochlore BZN Gate Dielectric on Polymer Substrate”, IEEE Transactions on Electron Devices, 52(12), p2819-2824, (2005).
[https://doi.org/10.1109/TED.2005.859594]

-
E. Celik, H. Park, H. Choi, and H. Choi, “Carbon nanotube blended polyethersulfone membranes for fouling control in water treatment”, Water research, 45(1), p274-282, (2011).
[https://doi.org/10.1016/j.watres.2010.07.060]

- Y. Yun, J. H. Jeong, H. S. Kim, and N. W. Jang, “A miniaturized impedance transformer on PES for flexible RFICs”, Microwave Journal, 57(2), p100-110, (2014).
-
Y. Yun, J. H. Jeong, H. S. Kim, and N. W. Jang, “Basic RF characteristics of fishbone-type transmission line employing comb-type ground plane (FTLCGP) on PES substrate for application to flexible passive circuit”, ETRI Journal, 37(1), p128-137, (2015).
[https://doi.org/10.4218/etrij.15.0114.0244]

-
Y. Yun, “A study on RF characteristics of fishbone-type transmission line on PES substrate for-application to flexible wireless communication device”, Journal of the Korean Society of Marine Engineering, 38(3), p302-311, (2014).
[https://doi.org/10.5916/jkosme.2014.38.3.302]

-
T. Fujii, I. Ohta, T. Kawai, and Y. Kokubo, “Miniature broad-band CPW 3-dB branch-line couplers in slow-wave structure”, IEICE Transactions on Electroics, E90-C(12), p2245-2253, (2007).
[https://doi.org/10.1093/ietele/e90-c.12.2245]

- D. M. Pozar, Microwave Engineering, 2nd ed, Chapter 4 Addison-wesley, (1990).
-
D. Ahn, J. S. Park, C. S. Kim, J. Kim, Y. Qian, and T. Itoh, “A design of low-pass filter using the novel microstrip defected ground structure”, IEEE Transactions on Microwave Theory and Techniques, 49(1), p86-93, (2001).
[https://doi.org/10.1109/22.899965]

-
A. Lai, and T. Itoh, “Microwave composite right/left-handed metamaterials and devices”, Proceeding of Asia-Pacific Microwave Conference, p31-34, (2005).
[https://doi.org/10.1109/apmc.2005.1606179]

- J. Gao, and L. Zhu, “Per-unit-length parameters of 1-D CPW metamaterials with simultaneously series-C and shunt-L loading”, Proceeding of Asia-Pacific Microwave Conference, p39-42, (2005).
-
F. R. Yang, K. P. Ma, Y. Qian, and T. Itoh, “A UC-PBG structure and its applications for microwave circuits”, IEEE Transactions on Microwave Theory and Techniques, 47(8), p1509-1514, (1999).
[https://doi.org/10.1109/22.780402]

-
A. S. Andrenko, Y. Ikeda, and O. Ishida, “Application of PBG microstrip circuits for enhancing the performance of high-density substrate patch antennas”, Microwave and Optical Technology Letters, 32(5), p340-344, (2002).
[https://doi.org/10.1002/mop.10173]