저속 회전형 소형 수직축 풍력발전기의 공기역학적 출력에 대한 CFD 및 실험적 검증

1. 서 론

최근 신재생에너지에 대한 연구가 활발히 진행 중이며 신재생에너지원 중에서 풍력에너지는 환경오염을 유발하지 않는 친환경 재생에너지로, 세계적으로 많은 연구 및 개발이 진행되고 있다[1][2]. 1997년 쿄토협약에서부터 2015년 파리기후협약에 이르면서 보다 많은 국가에서 산업화에 따른 기후변화 문제를 공감하고 있으며 이를 해결하기 위하여 풍력발전은 최적의 발전시스템으로 평가되고 있다[3]. 이 같은 사회적 분위기에서 풍력발전에 대한 연구가 활발히 이루어져 왔으나 소음 및 고속 회전으로 인한 시각적 위협감 등의 문제로 사회적 인식이 나빠지고 있는 실정이다[4].

이러한 배경을 통하여 본 연구에서는 출력 중심의 고속회전형 로터가 아닌 보다 저속으로 회전하는 소형 풍력발전기를 설계하여 해안가, 해안 관광지 또는 크루즈선 등 친인화적으로 설치가 가능하도록 하는 것이 목적이다.

본 연구에서 설계한 풍력발전기는 수직축 풍력발전기이며 바람의 방향과 무관하게 구동이 가능하며 요잉장치, 너셀 등의 장치가 필요 없어 설치 장소의 제한이 적으며 큰 정격출력보다는 꾸준히 높은 출력을 가져야 하는 소형 풍력발전기로 적합하다.

수직축 풍력발전기의 개념은 Darrieus에 의하여 1931년에 제안되었으며 이후, 현재에도 이에 대한 연구 및 개발이 진행 중이다[5].

기존 연구에서는 Templin[6]에 의하여 제안된 Single streamtube numerical model이 있다. 이는 단일 블레이드에 대한 성능을 계산하고 전체 로터의 출력은 로터 블레이드의 전체 시위길이를 반영한 단일 블레이드 성능과 동일하다고 제안하였다. 그리고 James H. [7]은 운동량과 Blade element theory를 보존하는 여러개의 Streamtube를 반영한 Multiple single streamtube model을 제안하였다. 이 밖에도 여러 가지 수학적 모델이 있다[8][9]. 그리고 실험적으로 성능을 검증하기 위한 연구도 Robert E. Sheldahl[10]과 Gabriele Bedon et al. [11] 등의 연구자들을 통하여 진행된 바가 있다. 컴퓨터의 발전에 따른 CFD를 이용한 연구도 많이 진행되어 왔다. Travis J. Carrigan et al. [12]는 2차원 CFD 기법을 이용하여 고정된 주속비에서 익형의 솔리디티 변화에 따른 출력 특성을 연구하였고 Joha A. Ekaterinaris et al. [13]은 CFD를 통하여 동실속에 대한 접근은 SST 난류 모델이 예측성이 우수하다는 결론을 제시하였다. 하지만 2D CFD의 경우, 직선형 블레이드 형상에만 적용 될 수 있으며 블레이드 끝단에서 발생되는 유동 특성 등이 반영되지 않아 출력을 과도하게 예측하는 단점이 있다.

본 연구에서는 헬리컬 형상의 블레이드를 가진 수직축 풍력발전기를 설계하여 3차원 CFD해석을 수행하여 출력 및 헬리컬 형상의 공력 특성을 분석하고 실제 크기의 로터를 이용하여 풍동시험을 수행하였으며 CFD 해석 결과의 신뢰성을 확인하였다. 이를 통하여 보다 다양한 형태의 수직축 풍력발전기 연구에 대한 절차를 확립할 수 있을 것으로 판단된다.

2. 소형 수직축 풍력발전기 설계

100 W급 소형 수직축 풍력발전기 설계를 위하여 정격 유입 풍속은 9 m/s로 IEC 61400-2의 소형 풍력발전시스템 등급의 Clase 1에 해당하는 풍속 10 m/s보다 낮은 풍속으로 Clase S에 해당된다.

여기서, P_t는 풍력발전기의 출력, A_w는 풍력발전기의 수풍면적, V_w는 정격 유입 풍속, C_p는 출력계수, η는 동력 전달 효율이다. 그리고 ρ는 공기 밀도이며 IEC 61400-2에서 제시한 1.225 kg/m³을 적용하였다.

출력 계수를 0.15로 정의하였으며 동력 전달 효율을 0.9로 정의하였다. 식 (1)을 통하여 수풍면적을 산출하였으며 식 (2)와 같이 종횡비를 반영하여 로터 반경과 높이를 결정하였다.

여기서, R_t는 로터 반경, H_t는 로터 높이이다.

익형은 NACA 0018을 적용하였으며 시위길이를 결정하기 위하여 아래의 식 (3)을 적용하였다.

여기서, σ는 솔리디티이며 0.3으로 정의하였고, B는 블레이드 개수, C는 시위길이이다.

마지막으로 회전수는 주속비 1.1의 저속회전을 목표로 하였으며 반경과 유입 풍속을 반영하여 170 rpm의 로터 회전수를 설정하였다.

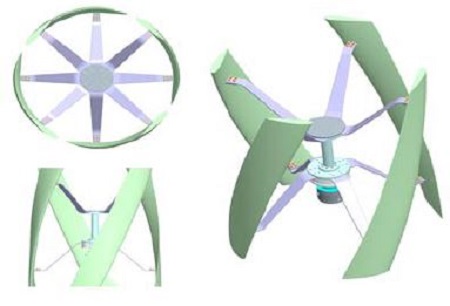
위의 식을 통하여 획득한 로터 설계 변수 값과 사양은 Table 1과 같다. 그리고 이를 바탕으로 구성된 3차원 로터 형상은 Figure 1과 같다.

Table 1:

Design specification of 100 W class helical type vertical axis wind turbine

Figure 1:

3-D model of 100 W class helical type vertical axis wind turbine rotor

3. 풍동 시험 및 전산유동해석

3.1 풍동 시험

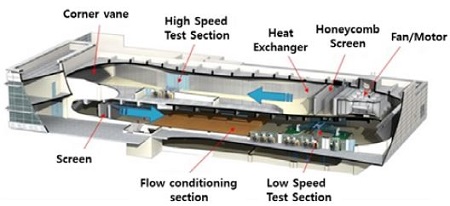
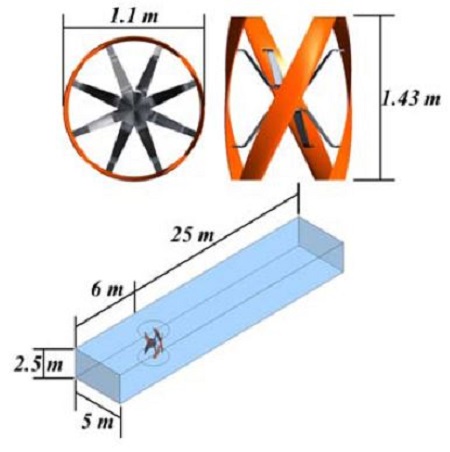
풍동 시험은 전북대학교 대형풍동실험센터에서 진행하였으며 풍동 시험기의 내부 구성도는 Figure 2와 같다. 너비 5 m, 높이 2.5 m 그리고 길이 20 m의 대형 풍동 시험기이다. 풍동 시험기의 사양은 Table 2에 나타내고 있다.

Figure 2:

Schematic of wind tunnel facility

Table 2:

Wind tunnel specifications

풍동 시험은 5 m/s에서 11 m/s까지 풍속을 변화하며 각각의 풍속에서 회전수에 따른 출력을 획득하였다. 로터 회전수는 제어기에서 가변 부하 제어를 통하여 변경하였다.

Figure 3은 풍동 시험에 사용된 실험 장비 구성을 나타내고 있다. 유입 풍속은 풍동 시험기에 설치된 풍속계를 통하여 획득하였으며 전류계 및 전압계를 사용하여 전력을 획득하였다. 그리고 발전기에서 생산된 전력을 흡수하기 위하여 파워싱커를 사용하였다. 로터의 회전수는 발전기의 3상 주파수를 통하여 추정하였다.

Figure 3:

Wind tunnel experimental setup

3.2 3차원 전산유동해석

유동해석에 사용될 유동장은 풍동시험기의 너비 5 m, 높이 2.5 m를 적용하였으며 길이 방향으로는 후류 영향에 의한 해석 안정성을 위하여 31 m로 확장하였다. Figure 4는 해석에 사용된 유동장을 나타내고 있다. 해석 영역은 풍력발전기 로터를 포함한 회전영역과 비회전 영역으로 분할하였다.

Figure 4:

3D flow field of wind tunnel test section included 100 W vertical axis wind turbine

해석을 위한 유한 요소 모델은 Figure 5와 같으며 사면체 격자계를 사용하였다. 또한 블레이드 주변의 유동 특성을 고려하여 보다 조밀한 격자계를 구성하였다. 블레이드를 포함한 모든 구조물과 벽면에는 벽면 점성 효과를 고려하여 프리즘 격자계를 배치하였다. 해석 격자계의 총 노드수는 10,425,181개 이며 이 중에서 회전 영역의 노드수는 9,813,123개 이다. Table 3은 해석에 사용된 격자계의 정보를 나타낸다.

Figure 5:

Mesh system of helical type vertical axis wind turbine for CFD analysis

Table 3:

Mesh information for 3D flow field

과도해석 조건으로 해석을 수행하였으며 시간 간격은 회전각도 1°에 해당하는 9.8e-4 sec를 적용하였다. 입구 유속은 정격 풍속인 9 m/s를 적용하였으며 난류 강도는 풍동 시험기 사양인 1.5%로 적용하였다. 난류 모델은 RANS 계열의 SST(Shear Stress Transport) 난류 모델을 적용하였다. Table 4에서는 경계조건에 대한 자세한 정보를 나타내고 있다[14].

Table 4:

Detail information of the CFD analysis

해석에 사용된 소프트웨어는 ANSYS CFX 15.0 이다.

4. 결 과

4.1 풍동 시험 결과

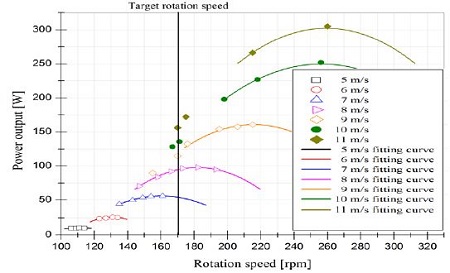
Figure 6에서는 각 풍속에 대하여 회전수별 출력을 보이고 있다. 풍속 증가에 따라 최대 출력 값이 급격하게 상승하는 것을 확인 할 수 있으며 이는 출력이 유입 풍속의 3승 비율로 증가하기 때문임을 식 (1)을 통하여 확인 할 수 있다.

Figure 6:

Graph of power output according to each wind velocity

Table 5는 각 풍속에서의 최대 출력값과 최대 출력 시 로터 회전수를 나타내고 있다. 그리고 8 m/s 이후의 풍속에서는 설계 회전수에 해당하는 170 rpm에서의 출력을 나타내고 있다. 3.5 m/s에서 기동을 시작하여 설계 풍속 9 m/s에서는 최대 160 W를 보이고 있다. 제어기의 제어를 통하여 회전수를 170 rpm으로 제어한 결과 114.7 W로 정격 출력 보다 약 14 % 높은 출력을 보이고 있다. 풍동시험기의 폐쇠효과를 고려했을 때 정격 출력을 충분히 만족한다고 판단된다.

Table 5:

Power output, Rotational speed according to the wind speed

4.2 전산유동해석 결과

Table 6에서는 3차원 전산유동해석에서 얻은 출력과 풍동 시험에서 얻은 출력을 비교하고 있다. 유동해석 결과는 약 11 % 정도 높은 출력을 보이고 있으며 이는 동력전달 손실이 반영되지 않은 결과이다. 풍동 시험에서는 로터의 기계적 출력이 발전기의 전기적 출력으로 변환되어 측정된 것이며 해석에서는 이러한 변환을 반영할 수 없기 때문에 위와 같이 높은 출력이 도출된 것이라 판단된다.

Table 6:

Comparison between wind tunnel results and CFD results (Wind speed : 9 m/s)

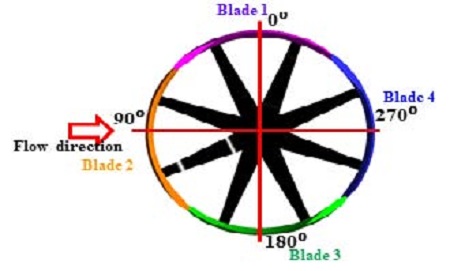
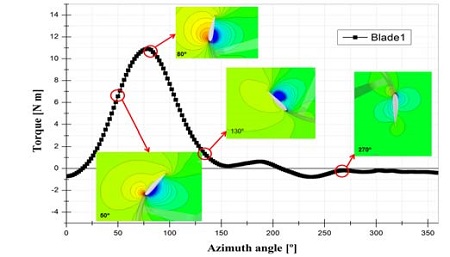
Figure 7은 블레이드의 위치와 방위각을 표현하고 있다. 로터 중심높이에서 Blade 1이 방위각 0°에 위치하고 있다. Figure 8은 방위각 0°에서 360°까지 Blade 1의 토크 변화를 나타낸 것이다. 바람의 유입 방향인 방위각 90° 주변에서 출력이 크게 기인하는 토크가 발생하고 있으며 180° 이후의 방위각에서는 발생되는 토크가 거의 없다. Blade 1 주변의 압력 분포에서도 토크가 많이 발생되는 방위각에서는 흡입면과 압력면의 압력차이가 크게 나타나고 있으며 그 외의 방위각 범위에서는 블레이드 주변 압력의 변화가 미비한 것을 확인 할 수 있다.

Figure 7:

Blade position and Azimuth angle

Figure 8:

Torque graph of Blade1 and pressure distribution around Blade1

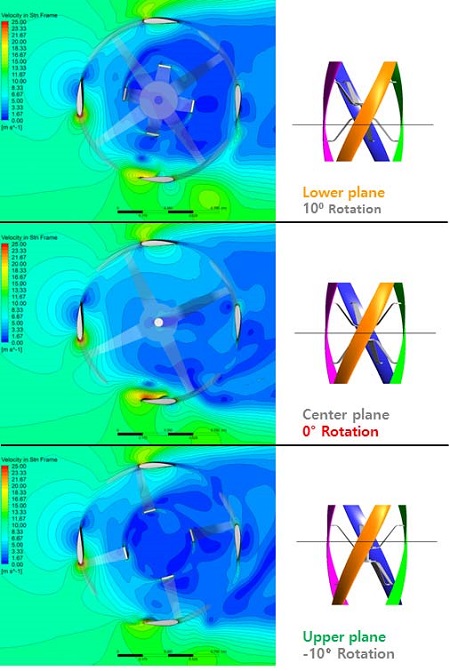
Figure 9는 헬리컬 형상에 의한 유동 특성을 분석하기 위한 그림이다. 헬리컬 로터가 10°, 0°, -10°로 회전하였을 때 블레이드 단면 위치가 동일한 높이에서의 속도 분포를 나타내고 있다. 로터의 회전 각도가 다르더라도 블레이드 단면의 위치가 동일한 높이에서 형성되는 속도 분포는 유사한 것을 확인 할 수 있다.

Figure 9:

Comparison of velocity distribution at same blade positions in each plane

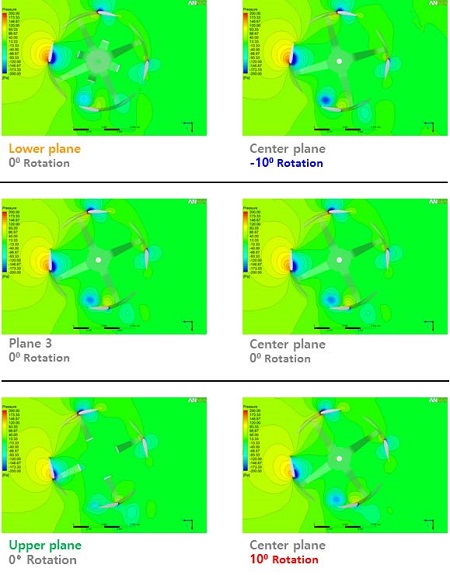
Figure 10은 로터 회전각도 –10°, 0° 10°에서의 단면 위치 별 압력 분포를 나타내고 있다. 로터가 회전함에 따라 중심단면에서 발생되는 압력분포와 동일한 로터 회전각도에서 높이방향으로 다른 위치에 있는 단면의 압력 분포가 동일하다는 것을 확인 할 수 있다. 이는 출력에 기여하는 토크 발생 범위에 블레이드가 진입할 때 헬리컬 형상에 의하여 높이 방향으로 연속적인 토크가 형성된다고 분석할 수 있다. 이러한 특성으로 인하여 직선형 블레이드에 비하여 출력 변동이 적게 나타나는 것이다.

Figure 10:

Comparison of pressure distribution between difference plane position and difference rotation angle

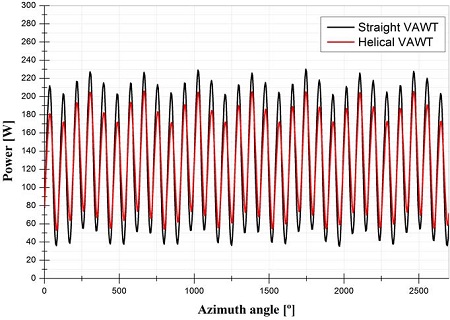
Figure 11은 동일한 블레이드 시위길이, 반경, 높이를 가지는 직선형 로터와 헬리컬 로터의 출력 변동을 비교한 것이다. 회전에 따른 출력의 평균값의 차이는 거의 없으나 헬리컬 로터의 출력변동이 약 10 %정도 작은 것을 확인 할 수 있다. 이러한 원인은 앞서 확인한바와 같이 연속적으로 발생하는 압력특성에 의한 토크 변동이 적기 때문이다.

Figure 11:

Comparison of power output between helical type vertical axis wind turbine and straight type vertical axis wind turbine

5. 결 론

본 논문에서는 100 W급 헬리컬 수직축 풍력터빈을 설계하였으며 설계된 로터에 대한 3차원 전산유동해석에서 얻은 출력 결과와 풍동 시험에서 얻은 출력 결과를 비교하여 설계 및 해석 기법의 타당성을 확인하였다.

수직축 풍력발전기는 9 m/s의 풍속에서 170 rpm의 회전으로 100 W의 출력을 가지도록 설계되었으며 풍동 시험에서 114.7 W의 출력을 얻었으며 폐쇠효과를 고려한다면 설계 출력과 거의 일치한다.

또한 풍동 시험 조건을 반영한 3차원 전산유동해석을 통하여 127.7 W의 출력을 얻었으며 풍동 시험 결과와 비교하였을 때 11 % 정도 큰 출력 결과를 획득하였고 부차 손실 및 동력 전달 효율을 감안한다면 충분한 타당성을 확보할 수 있었다. 그리고 유동해석을 통하여 헬리컬 형상이 가지는 공력 특성을 분석하였다. 출력에 기여하는 토크를 형성하는 회전 범위에 진입할 때 꼬여있는 블레이드 형상은 연속적인 토크를 발생하여 출력 변동이 낮아짐을 확인하였다.

References

• K. C. Tong, “Technical and economic aspects of a floating offshore wind farm”, Journal of Wind Engineering and Industrial Aerodynamics, 74-76, p399-410, (1998). [https://doi.org/10.1016/S0167-6105(98)00036-1]
• A. S. A. Shata, and R. Hanitsch, “Evaluation of wind energy potential and electricity generation on the coast of mediterranean sea in Egypt”, Renewable Energy, 31(8), p1183-1202, (2006). [https://doi.org/10.1016/j.renene.2005.06.015]
• Small and Medium Business Administration, Technology Road Map for SME, 2015-2017, (2015).
• B. Greening, and A. Azapagic, “Environmental impacts of micro-wind turbines and their potential to contribute to UK climate change targets”, Energy, 59, p454-466, (2013). [https://doi.org/10.1016/j.energy.2013.06.037]
• G. Darrieus, “Turbine having its rotating shaft transvers to the flow of the current”, U.S. Patent 1835018, (1931, Dec, 8).
• R. J. Templin, Aerodynamic Performance Theory for the NRC Vertical-axis Wind Turbine, Laboratory Technical Report LTR-LA-160, National Research Council, Canada, (1974).
• J. H. Strickland, The Darrieus Turbine : A Performance Prediction Model Using Multiple Streamtubes, Laboratory Technical Report SAND74-0431, USA, (1975).
• M. Islam, D. S. K. Ting, and A. Fartaj, “Aerodynamic models for darrieus-type straight-bladed vertical asix wind turbines”, Renewable and Sustainable Energy Reviews, 12(4), p1087-1109, (2008). [https://doi.org/10.1016/j.rser.2006.10.023]
• I. Paraschivoiu, “Double-multiple streamtube model for studying vertical-axis wind turbines”, Journal of Propulsion and Power, 4(4), p370-377, (1988). [https://doi.org/10.2514/3.23076]
• R. E. Sheldahl, “Comparison of field and wind tunnel darrieus wind turbine data”, Journal of Energy, 5(4), p254-256, (1981). [https://doi.org/10.2514/3.48036]
• G. Bedon, M. R. Castelli, and E. Benini, “Experimental tests of a vertical-axis wind turbine with twisted blades”, ICMIME 2013, p384-387, (2013).
• T. J. Carrigan, B. H. Dennis, Z. X han, and B. P. Wang, “Aerodynamic shape optimization of a vertical-axis wind turbine using differential evolution”, ISRN Renewable Energy, 2012, Article ID 528418, (2012). [https://doi.org/10.5402/2012/528418]
• J. A. Ekaterinaris, and M. F. Platzer, “Computational prediction of airfoil dynamic stall”, Progress in Aerospace Sciences, 33(11-12), p759-846, (1998). [https://doi.org/10.1016/S0376-0421(97)00012-2]
• F. R. Menter, “ZONAL TWO EQUATION k-ω TURBULENCE MODELS FORAERODYNAMIC FLOWS”, AIAA Fluid Dynamics Conference, (1993).