스트레인 게이지를 이용한 5만 DWT급 석유화학제품운반선의 베어링 반력 및 선체변형량 분석에 관한 연구

1. 서 론

축계정렬에 관한 연구는 1950년대 후반 미국 해군 함정에서 그 중요성이 대두된 이후 1960년대 후반부터 1970년대 초반에 걸쳐 개개의 베어링에 대한 최적의 위치를 결정하는 주요 이론이 정립되었다[1]-[4]. 이후 조선기술 및 철강기술의 발전과 함께 선박은 고출력화, 대형화 됨에 따라 추진축의 강성은 증가한 반면 선체는 고장력 후판의 적용으로 이전의 선체보다 훨씬 더 쉽게 변형되는 실정이다. 이는 기존의 선박보다 더욱 정교한 축계정렬이 요구됨을 의미한다. 따라서 최적의 축계정렬상태를 설계 단계에서 얻기 위해서는 해석 시 선박의 적하 하중에 따른 베어링 반력의 변화, 운항에 따른 메인 엔진의 변형 및 프로펠러 추력에 의해 발생되는 굽힘모멘트, 하중에 대해 연직방향으로 작용하는 베어링의 탄성변형 등을 함께 고려하여[5]-[10] 추진축계와 주 구동장치에 민감한 영향을 미치지 않도록 넉넉한 허용범위를 갖도록 하는 것이 바람직하다. 흘수 변화에 의한 선체의 변형상태는 유한요소 해석을 통해 예측이 가능하지만 많은 시간과 비용이 요구되며 계산의 정밀도를 결국 실측[11]-[16]으로 검증할 필요가 있다. 선체 변형에 대한 연구는 주로 선급이나 조선소에서 한 두척의 선박에 대해 연구목적으로 수행되었기 때문에 실제 그 데이터를 이용하여 축계정렬을 설계하는 데는 한계가 있다. 이를 개선하기 위하여 스트레인 게이지법을 이용하여 선종별로 추진축계에 영향을 미치는 선체변형에 대한 역계산 연구가 수행되었지만[17] 최근 등장한 5만톤급 중형 석유화학제품 운반선(MR tanker)에 대한 연구 사례는 아직까지 없었다. 5만톤급 MR 탱커는 유사선 대비 새로운 형식의 기관을 탑재하고 부하 경감(De-rating) 기술을 적용하여 연료 소모량 감소를 극대화 하였으며, 이로 인해 낮아진 기관 회전수를 직경이 증가된 프로펠러 적용을 통해 보상하여 추진 효율을 극대화 시킨 친환경 고효율 선박이다. 따라서 본 연구에서는 5만톤급 MR 탱커에 대하여 스트레인게이지를 이용한 계측을 수행하고 측정된 자료를 이용하여 베어링 반력 및 선체 변형량을 분석하였다. 측정은 선박의 통상 흘수 변화에 따라 5개 조건에서 수행되었고 추진축계가 선체 변형의 영향 하에서도 허용치[18]를 만족하는지 여부를 확인하였다.

또한 이론적 계산방법, 잭업법 및 스트레인 게이지법의 결과를 상호 비교하여 해석의 신뢰성을 교차 검증하였다.

2. 계측 및 데이터 분석방법

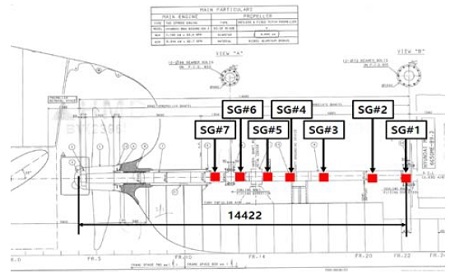
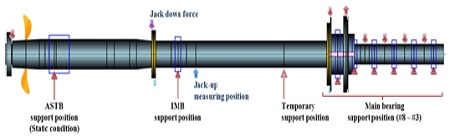
Table 1 은 본 연구에 이용한 실선의 축계 주요 사양이며 Figure 1 은 축계 배치도 및 굽힘 모멘트 측정을 위한 스트레인 게이지 부착위치를 나타내었다.

Table 1:

Specification of shafting system

Figure 1:

Shafting arrangement and allocated strain gauge position

스트레인 게이지는 선미측 스트레인 게이지를 SG#7로 하여 총 7 개소에 축의 종방향에 걸쳐 설치하였다. Table 2 에 프로펠러축 끝단을 기준으로 스트레인게이지의 설치 위치를 나타내었으며 Figure 2에서는 스트레인 게이지의 모습과 연결상태를 나타내었다.

Table 2:

Position of strain gauges by axial location

Figure 2:

General half bridge configuration and installation of telemetric strain gauge system on the shafts

본 연구에서는 TML (Tokyo sokki kenkyujo)사의 WFLA-3-11-L1 스트레인 게이지를 사용하였으며 하프 휘트스톤 브릿지(half whitstone bridge) 방식으로 구성하였고 게이지는 축의 상단과 하단에 180도 간격을 두고 각 1조씩 부착하였다. 응력 은 터닝 기어를 이용하여 축을 한 바퀴에서 두 바퀴 정도 회전시켜 측정하였다. 회전시 축의 굽힘으로 인해 스트레인 게이지로부터 전압 값이 얻어지는데 이를 통해 식 (1)과 같이 굽힘모멘트를 구할 수 있다.

여기서 E는 종탄성계수, D_o는 축의 외경, D_i는 축의 내경, ϵ는 스트레인 게이지로부터 측정된 응력으로서 식 (2)와 같이 표현된다.

여기에서 V_o는 휘트스톤 브릿지에서 측정된 출력전압 값이고 V_ek는 휘트스톤 브릿지의 입력전압이다. 본 연구에서는 대략적으로 10V의 V_ek값이 사용되었다. k는 스트레인 게이지 상수이다.

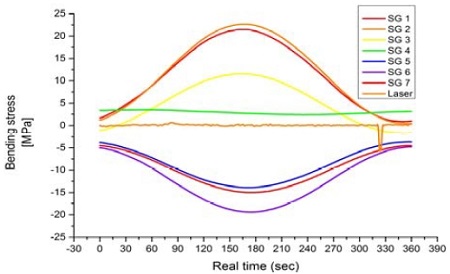
스트레인 게이지로부터 얻어진 데이터는 PC로 전송되고 PC에 설치된 HBM사의 Catman 데이터 측정 소프트웨어를 통해 모아진 정보를 굽힘응력으로 전환한다. 전환된 굽힘 응력에 축의 단면계수를 곱하면 굽힘 모멘트를 최종적으로 구할 수 있다. Figure 3은 축을 1회전 하였을 때 얻어진 굽힘응력 선도를 보여주며 Table 3 은 여러 흘수 조건에서의 축 굽힘 모멘트 값을 정리한 결과이다.

Figure 3:

Measured bending stress at ballast APT full condition

아래 Table 3에 표기된 흘수조건은 다음과 같다.

Table 3:

Processed bending moments from stain gauge under five(5) draught condition

D1: Light ballast APT empty (aft: 6.6m fore: 3.4m)

D2: Scantling APT full (aft: 12.6m fore: 13.2m)

D3: Scantling APT empty (aft: 12.5m fore: 13.5m)

D4: Ballast APT empty (aft: 7.9m fore: 6.3m)

D5: Ballast APT full (aft: 8.95m fore: 6.45m)

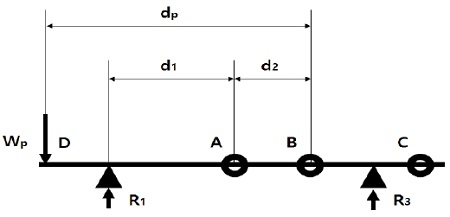
다음으로 선미관 베어링 반력 R₁의 해석을 위하여 각 변수를 Figure 4에 따라 정의하고 모멘트 평형방정식을 수립하면 아래 식 (3)과 같이 나타낼 수 있다.

Figure 4:

Layout diagram of stern tube bearing

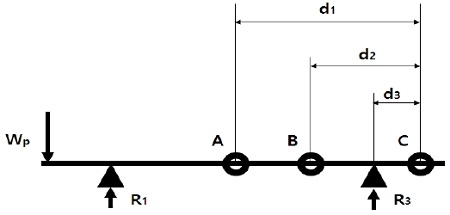
여기서 A, B, C는 스트레인 게이지를 나타내며 D는 프로펠러 중량이 작용하는 질점을 나타낸다. 또한, 게이지로부터 해당 지점까지의 거리를 d₁, d₂, d_p라 한다. M_A는 A점에서의 측정 모멘트, M_AD는 AD지점간 축중량에 의한 모멘트이며 W_p는 프로펠러 중량을 나타낸다. 마찬가지로 중간축 베어링 반력 R₃의 해석은 상기와 같은 방식으로 각 변수를 Figure 5에 따라 정의하고 모멘트 평형방정식을 수립하면 아래 식 (4)와 같이 나타낼 수 있다.

Figure 5:

Layout diagram of intermediate shaft bearing

여기서 A,B,C는 스트레인 게이지를 나타내며 게이지로 부터 해당지점까지의 거리를 d₁, d₂, d₃라 한다. M_A, M_B, M_C는 각 점에서의 측정 모멘트, M_AB, M_BC는 지점간 축중량에 의한 모멘트를 나타낸다.

3. 선체변형량 예측 및 베어링 반력계산결과

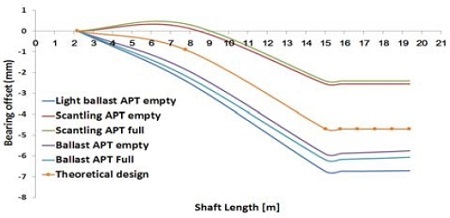
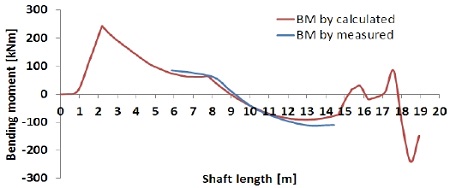
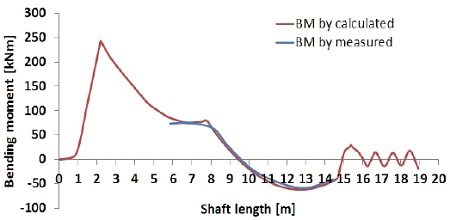
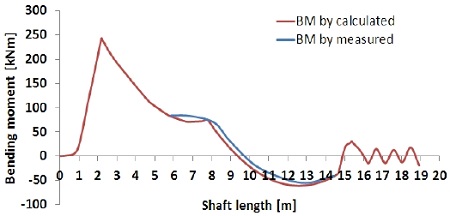
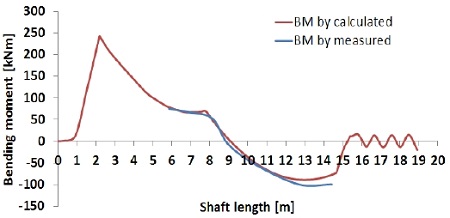
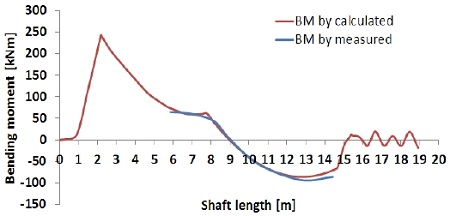
통상 선체 변형량 예측 기법에는 크게 유한요소법을 이용한 해석, 계측치를 이용하는 역해석 기법이 있다. 역해석 기법은 스트레인 게이지로부터 도출한 굽힘 모멘트정보와 게이지의 위치정보, 잭업법으로 계측된 베어링 반력정보가 있으면 역계산 프로그램을 이용하여 선체변형을 예측하는 것이 가능하다[19][20]. 그러나 현재까지 국내기술로 개발된 축계 역계산 프로그램 활용에 대한 연구결과는 매우 적은 것이 현실이다. 이에 대한 대안으로써 축계정렬 프로그램으로 계산한 굽힘모멘트 선도가 계측치와 일치하는 지점을 시행착오(try and error) 기법으로 찾음으로써 선체 변형량을 예측할 수 있다. 저자는 현재 축계 역계산 프로그램을 개발 중에 있으며 본 연구의 후속으로 그 신뢰성을 검증할 계획이다. 따라서 Figure 6과 같이 축계 모델을 생성하여 시행착오(try and error) 기법으로 예측한 본 선박의 선체 변형량은 Table 4 및 Figure 7와 같으며 Figure 8 ~ Figure 12에 각 흘수조건의 계측치로 환산한 굽힘모멘트와 축계정렬프로그램[21]으로 계산한 굽힘모멘트와의 비교결과를 나타내었다. 분석결과 양 기법간 매우 유사한 경향이 나타남을 확인하였으며 이를 통해 선체 변형량 예측의 신뢰도를 확인할 수 있었다.

Figure 6:

Shaft alignment calculation model

Table 4:

Estimated bearing offsets based on strain gauge measurement

Figure 7:

Estimated hull deflection based on strain gauge measurement

Figure 8:

Bending moment comparison at D1

Figure 9:

Bending moment comparison at D2

Figure 10:

Bending moment comparison at D3

Figure 11:

Bending moment comparison at D4

Figure 12:

Bending moment comparison at D5

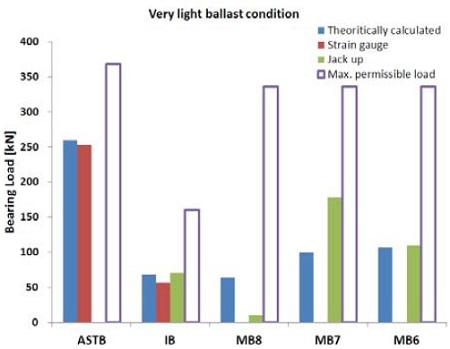
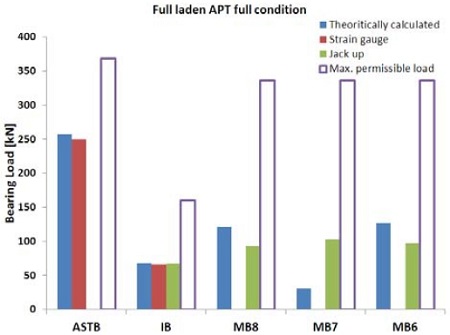
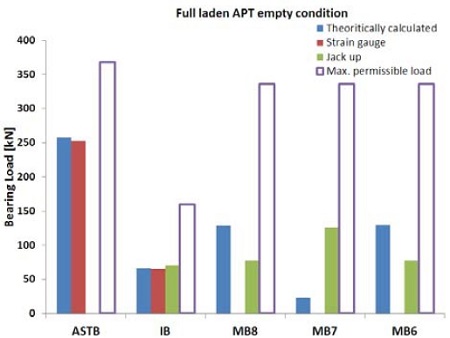
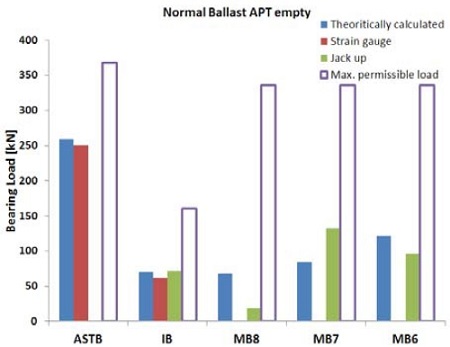
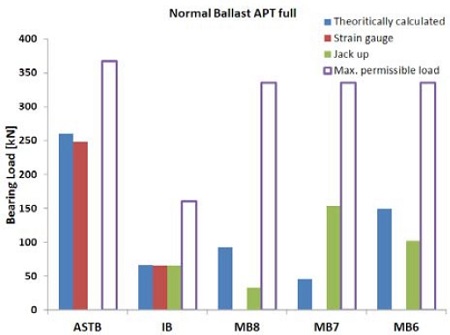
또한 흘수 변화에 따른 선체변형량은 중간축 베어링에서 2mm, 주기관 베어링에서 4mm 정도로 예측되었다. 따라서 대상선박이 이러한 선체 변형의 영향 하에서도 축 지지베어링의 반력변화가 허용치 이내를 만족하는지 여부를 검토하였다. 또한 해석의 신뢰도를 높이기 위하여 이론적 방법, 잭업법 및 스트레인 게이지법을 상호 비교하여 허용치와 함께 Table 5 및 Figure 13 ~ Figure 17에 나타내었다. 여기서 ASTB, IB, MB는 각각 선미관베어링, 중간축베어링, 주기관베어링을 의미한다.

Table 5:

Correlation among three technics under vessel’s five(5) condition

Figure 13:

Correlation among three technics at D1

Figure 14:

Correlation among three technics at D2

Figure 15:

Correlation among three technics at D3

Figure 16:

Correlation among three technics at D4

Figure 17:

Correlation among three technics at D5

잭업법은 중간축 베어링, 주기관베어링과 같이 유압 잭을 근접설치 할 수 있는 곳에서 작업을 비교적 용이하게 실시할 수 있지만 선미관 베어링 근처에는 유압 잭 설치가 불가능하므로 측정할 수 없는 단점이 있다. 반면 스트레인게이지 법은 설치 시 시간이 많이 소요되는 문제가 있지만 모멘트 평형방정식을 이용하여 선미관 베어링의 반력을 계산할 수 있는 장점이 있다. 중간축 베어링 측정 및 계산은 상기 양 기법 모두에 공통적으로 해당되므로 중간축 베어링 반력의 일치여부 확인을 통해 상호간의 신뢰성을 교차검증할 수 있다. 검토결과 중간축 베어링의 반력은 대부분의 조건에서 잘 일치하고 있음을 알 수 있었으며 따라서 선미관 베어링의 반력 또한 높은 신뢰도를 가지고 있는 것으로 판단된다. 실측된 주기관 크랭크축 베어링의 반력은 비록 허용치 이내를 충분히 만족하고 있지만 이론적 분석결과 대비 차이가 있음을 알 수 있다. 이는 축계정렬계산을 위한 모델링 시 사용되는 크랭크축 부분이 엔진 제작사에서 제공하는 단순 등가 2차원의 모델이므로 실제 크랭크축 웹(Web)의 굽힘강성을 반영하지 못하기 때문인 것으로 판단된다. 또한 베어링 영향계수 값을 고려할 필요가 있는데 계산결과를 기준으로 MB8, MB7, MB6 베어링의 영향계수는 각각 1,360 kN/mm, 4,360 kN/mm, 3,430 kN/mm로써 매우 큰 값을 가진다. 이는 베어링 옵셋의 작은 변동이라도 주기관 베어링 하중에 큰 영향을 주게 됨을 의미한다. 이러한 옵셋의 변동은 주기관 베드 플레이트(bed plate)의 색(sag) 허용공차, 주기관 베어링 중심간의 허용편차, 실제 엔진이 설계된 것보다 더 경사지게 설치되었을 경우에 발생할 수 있는 일반적인 현상으로 판단되므로 크랭크축 베어링에 부정적인 형향을 미치지 않을 것으로 판단된다.

4. 결 론

본 연구에서는 새로운 선형인 5만톤급 중형화학제품운반선을 대상으로 스트레인 게이지법으로 축계의 굽힘모멘트를 측정하여 선체변형량을 예측하고 축계의 베어링 반력을 분석하였다. 또한 측정결과를 잭업법 및 이론적 분석결과와 교차검증하여 다음과 같은 결과를 얻었다.

• (1) 스트레인게이지법을 이용하여 분석한 선체변형량은 중간축 베어링에서 2mm, 주기관 베어링에서 4mm정도로 예측되었다.
• (2) 5만톤급 석유화학제품 운반선의 선체 변형량은 기존의 4만6천톤급에서 예측된 변형량[17]인 중간축 베어링에서 1.4mm 주기관 베어링에서 1.24mm에 비해 다소 증가하였는데 이는 프로펠러 중량 및 주기관 중량이 증대된 것과 프로펠러 직경의 증가로 인한 선미부 변경이 주 원인으로 판단된다.
• (3) 선체 변형 하에서도 축계지지베어링의 반력은 허용치를 충분히 만족하고 있으며 이는 설계자가 선체변형의 경험치를 선 반영한 결과로 판단된다.
• (4)스트레인게이지법과 잭업법, 이론적 계산법으로 구한 베어링 반력을 교차 검증한 결과 대부분의 조건에서 양호한 일치를 보여 해석의 신뢰성을 확인할 수 있었다.
• (5) 본 연구에서 제공한 선체변형량은 향후 유사선박의 축계정렬 검토 시 참고가 될 것으로 판단된다.

References

• R. Michel, “A quarter century of propulsion shafting design practice and operating experience in the U.S. Navy”, Journal of the American Society of Naval Engineers, 71(1), p153-164, (1959). [https://doi.org/10.1111/j.1559-3584.1959.tb05306.x]
• H. C. Anderson, and J. J. Zrodowski, “Co-ordinated alignment of line shaft, propulsion gear, and turbines”, Annual Meeting of Society of Naval Architects and Marine Engineers, p449-523, (1959).
• W. E. Lehr, “Considerations in the design of marine propulsion shaft system”, The International Journal of Society of Naval Architects and Marine Engineers, 69, p555-601, (1961).
• G. Mann, “Shipyard alignment of propulsion shafting using fair curve alignment theory”, Journal of the American Society of Naval Engineers, 77(4), p651-659, (1965). [https://doi.org/10.1111/j.1559-3584.1965.tb04996.x]
• American Bureau of Shipping, Guidance Notes on Propulsion Shafting Alignment, Houston, USA, American Bureau of Shipping, (2006).
• K. C. Kim, and J. G. Kim, “A study on optimum shaft alignment analysis for VLCC”, Proceedings of the Special Transactions of the Society of Naval Architects of Korea, p134-137, (2005), (in Korean).
• Class NK, Guidelines on Shafting Alignment, Japan, Class NK, (2006).
• H. J. Jeon, Ship Propulsion Transmission Equipment, Busan, Korea, Taehwa Publishing Company, (1986), (in Korean).
• C. O. Seo, A Study on the Optimal Shafting Alignment for Chemical Tanker of Medium Size, M.S. Thesis, Department of Marine System Engineering Graduate School, Korea Maritime University, Korea, (2010), (in Korean).
• J. U. Lee, A study on the Optimal Shafting Alignment Concerning Bearing Stiffness for Extra Large Container Carrier, M.S. Thesis, Department of Marine System Engineering Graduate School, Korea Maritime University, Korea, (2010), (in Korean).
• R. B. Grant, “Shaft alignment methods with strain gages and load cells”, Marine Technology, 17(1), p8-15, (1980).
• A. W. Forrest, and R. F. Labasky, “Shaft alignment using strain gages”, Marine Technology, 18(3), p276-284, (1981).
• M. N. K. Rao, M. V. Dharaneepathy, S. Gomathinayagam, K. Ramaraju, and P. K. Chakravorty, “Computer-aided alignment of ship propulsion shafts by strain gage methods”, Marine Technology, 28(2), p84-90, (1991).
• H. C. Jung, K. S. Kim, W. S. Jang, and S. S. Na, “A study on shaft alignment of the rotating machinery by using strain gages”, Journal of the Korean Society for Precision Engineering, 19(5), p126-132, (2002), (in Korean).
• L. Shi, D. Xue, and X. Song, “Research on shafting alignment considering ship hull deformations”, Marine Structures, 23(1), p103-114, (2010). [https://doi.org/10.1016/j.marstruc.2010.01.003]
• S. D. Zhang, J. G. Yang, Y. Y. Li, and J. Li, “Identification of bearing load by three section strain gauge method: Theoretical and experimental research”, Measurement, 46(10), p3968-3975, (2013). [https://doi.org/10.1016/j.measurement.2013.07.017]
• Y. J. Lee, A Study on Hull Deflections Effecting the Ship’s Propulsion Shafting Alignment, Ph.D. Disseretation, Department of Mechanical Engineering Graduate School, Korea Maritime University, Korea, (2006), (in Korean).
• MAN B&W, “Bearing load measurement by jaking up”, ID No. 07424-5, (2012).
• D. Sverko, Journal of Society of Naval Architects and Marine Engineers, http://www.sname.org/HigherLogic/System/DownloadDocumentFile.ashx?DocumentFileKey=52f30429-0459-430d-ba5f-e2387c09b724 Accessed May 25, 2016.
• Y. Batrak, R. Batrak, and D. Berin, “Computer application for shaft alignment design”, International Conference on Computer Applications in Shipbuilding, (2013), [Online]. Available: http://www.academia.edu/4882690/COMPUTER_APPLICATION_FOR_SHAFT_ALIGNMENT_DESIGN.
• Korean Register, SeaTrust-Machinery, User Manual, ver.1.0, Busan, Korea, Korean Register, (2013), (in Korean).