[ Original Paper ]

Journal of the Korean Society of Marine Engineering - Vol. 40, No. 4, pp.275-281

ISSN: 2234-7925 (Print) 2234-8352 (Online)

Print publication date May 2016

Received 09 Mar 2016 Revised 11 May 2016 Accepted 19 Mar 2016

DOI: https://doi.org/10.5916/jkosme.2016.40.4.275

저압에서의 과냉각 비등 현상에 대한 CFD의 유효성 검토

최용석¹ ; 김유택² ; 임태우^†

CFD validation for subcooled boiling under low pressure

Yong-Seok Choi¹ ; You-Taek Kim² ; Tae-Woo Lim^†

1Division of Marine Engineering, Korea Maritime and Ocean University, Tel: 051-410-4256 choiys@kmou.ac.kr
2Division of Marine System Engineering, Korea Maritime and Ocean University, Tel: 051-410-4258 kimyt@kmou.ac.kr

Correspondence to: ^†Division of Marine Engineering, Korea Maritime and Ocean University, 727, Taejong-ro, Yeongdo-gu, Busan 49112, Korea, E-mail: kyunlim@kmou.ac.kr, Tel: 051-410-4256

Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록

본 연구에서는 전산유체역학(CFD)을 이용하여 저압에서의 과냉각 비등 현상에 대한 수치해석적 연구를 수행하였다. 과냉각 비등 현상을 시뮬레이션하기 위해서 벽비등 모델을 사용하였으며, 벽비등 모델은 기포 이탈 직경, 핵 사이트 밀도 그리고 기포 이탈 빈도로 구성된 하위모델을 필요로 한다. 전산유체역학 코드 CFX는 실험 자료에 근거한 기본 모델을 제공한다. 하지만 이러한 모델은 대부분 고압조건에서 개발되었기 때문에 저압조건에서는 잘 맞지 않는 것으로 보인다. 따라서 본 연구에서는 저압조건에서 과냉각 비등 현상에 대해서 CFD의 유효성을 검토하였다. 수치해석적 결과는 기존의 실험 결과와 비교하였다. 수치해석은 질량유속 250~750 kg/m²s, 열유속 0.37~0.77 MW/m² 그리고 출구압력 0.11 MPa범위에서 수행되었다. 저압조건에서 개발된 상관식을 적용함으로써 수치해석의 정확성을 높일 수 있었다.

Abstract

Subcooled boiling under low pressure was numerically investigated using computational fluid dynamics(CFD). The wall boiling model was used for simulating the subcooled boiling; this model requires sub-models consisting of bubble departure diameter, nucleation site density and bubble departure frequency. The CFD code CFX provides the default models based on experimental data. Because these models are mostly developed under high pressure conditions, it would not be predicted well in low pressure conditions. Thus in this study, CFD validation for subcooled boiling under low pressure was analyzed. The numerical results were compared with experimental data from published paper. Simulations were performed with mass flux ranging from 250 to 750 kg/m²s, heat flux ranging from 0.37 to 0.77 MW/m² and constant outlet pressure of 0.11 MPa. Employing the empirical correlation developed under low pressures could increase the accuracy of numerical analysis.

Keywords:

Bubble departure frequency, CFD, Nucleate site density, Subcooled boiling, Wall boiling model

키워드:

기포 이탈 빈도, 전산유체역학, 핵 사이트 밀도, 과냉각 비등, 벽 비등 모델

1. 서 론

과냉각 비등이란 가열면 부근에서 국부적으로 비등이 발생하지만 액체의 평균온도는 포화온도 보다 낮게 유지 되는 현상을 의미한다. 비등을 위한 가열면의 실질적인 온도는 작동유체의 포화온도보다 높아야 하며, 가열면의 온도가 일정 수준이상이 되면 핵비등이 시작된다. 이때를 핵비등 시발점(onset of nucleate boiling, ONB)이라고 한다. 일단 비등이 시작되면 핵 사이트(nucleation site)에서 생성된 기포는 유동하는 과정에서 포화온도보다 낮은 온도의 액체 속에서 응축되어 소산되는 과정을 거치며 열전달이 이루어진다.

이러한 2상 유동 열전달은 단상 유동에 비해서 높은 열전달 계수를 가지기 때문에 효과적으로 열을 소산시킬 수 있다. 이러한 장점은 여러 산업분야에서 효과적으로 적용되고 있다. 일반적인 열교환기에서 널리 이용되며, 특수한 분야로는 핵발전소의 원자로 냉각 등에 적용된다.

특히 원자로의 냉각의 경우 대부분의 연구에서 관심을 가지는 것은 기공률(void fraction)을 예측하는 것이다[1][2]. 내부 유동 시 기포의 거동에 의해서 유동양식이 분류되며, 이러한 유동양식은 열전달 계수의 변화에 막대한 영향을 끼치기 때문이다[3]. 이러한 이유로 기공률을 정확하게 예측하는 것은 원자로의 냉각 성능을 결정하여 설계하기 위한 필수적인 요소 중 하나이다.

하지만 원자로의 특성상 고온, 고압의 작동조건에 의해서 실험하기가 매우 까다롭기 때문에 일찍이 computational fluid dynamics(CFD)에 의한 수치해석적 연구가 도입되어 현재까지도 많은 연구가 이루어지고 있다[4]-[8]. CFD 연산 장치의 성능은 계속해서 발달하고 있으며, CFD의 사용 빈도는 점차 증가하고 있는 실정이다. CFD는 현재까지 많은 상용코드들과 오픈소스들이 개발되었으나, 2상 유동해석의 경우 메커니즘의 복잡성으로 인해서 정확도가 낮은 편이다. 또한 2상 유동의 경우 물리적인 현상을 모사하기 위한 많은 모델들이 개발되었으며, 이러한 모델을 적절하기 활용하기 위해서는 엔지니어의 높은 이해도가 요구된다.

Krepper et al.[1]은 CFD 상용코드인 CFX의 벽비등 모델(wall-boiling model)을 적용하여 Bartolomej and Chanturiya[9]의 실험 결과와 비교하였다. 그 결과, 3-11MPa의 압력, 1.2MW/m² 이상의 열유속 그리고 1000kg/m²s 부근의 질량유속에서 그 유효성을 입증하였다.

Chen et al.[10]은 저압영역인 0.269MPa에서 수행된 실험 결과를 토대로 과냉각 비등 모델을 수정하여 제안하였다. 기존의 과냉각 비등 모델의 경우 액체와 기체의 물성치를 포화압력, 포화온도에서의 값으로 고정하여 사용하였지만, 수정된 모델의 경우 온도에 따른 액체의 물성치 변화를 적용하여 유동 방향에 따라서 포화온도를 종속변수로 취급하였다.

Cheung et al.[11] 또한 저압조건에서 과냉각 비등에 관한 수치해석적 연구를 수행하였다. 축방향[12]과 반경방향[13][14]에 대한 기공률 분포 결과를 CFD 결과와 비교하였다. 상용코드에서 기본적으로 제공하는 모델 이외에 기포 이탈 직경과 핵 사이트 밀도(nucleation site density)를 계산하기 위한 다양한 모델[15]-[19]을 적용하여 비교하였다.

Kim et al.[20]은 하향경사 채널에서의 비등에 관한 실험적 연구와 수치해석적 연구를 진행하였다. 실험은 대기압 조건에서 수행되었다. 실험 결과를 기반으로 핵 사이트 밀도를 예측하는 기존의 상관식[19]을 수정하여 제안하였으며, 수치해석을 통해 입증하였다.

Krepper et al.[1]이 입증한 것과 같이 현재 CFD 상용코드의 비등 모델은 대부분 고압영역에서 적합하도록 구성되어 있다. 이러한 모델은 저압영역에서는 정확성이 떨어지는 것으로 나타났으며, 실제로 적용하기에는 어려움이 있을 것으로 사료된다. 따라서 대기압 영역에서 작동되는 시스템을 적절하게 모사하기 위해서는 저압영역에서의 과냉각 비등 현상을 구현할 수 있는 모델의 적용이 필요하다. 본 연구에서는 0.11MPa인 저압 영역에서의 수행된 과냉각 비등 실험 결과[21]를 토대로 CFD 상용코드 중 하나인 CFX 13.0을 사용하여, 대기압 부근인 저압영역에서 적용할 수 있도록 검토하였다. 벽비등 모델의 하위 모델에 상용코드에 내장되지 않은 여러 상관식들을 적용하여, 그 결과를 실험 결과[21]와 비교하였다.

2. 수치해석

2.1 벽비등 모델

상용코드에서 주로 사용되는 벽비등 모델은 Kurul and Podowski[22]의 Rensselaer Polytechnic Institute(RPI) wall boiling model을 사용하며, RPI wall boiling model은 열유속 분할 모델(heat flux partitioning model)을 기반으로 한다. 식 (1)과 같이 벽면에 전달된 전체 열(Q_total)은 각각 난류 대류(turbulent convection, Q_c), 급속냉각(quenching, Q_q), 증발(evaporation, Q_e)에 의해서 전달되는 것으로 표현할 수 있다.

Q total = Q c + Q q + Q e

(1)

난류 대류에 의한 열전달은 가열면에서 단상 액체에서 발생되며, 식 (2)와 같이 정의된다.

Q c = A 1 ρ l c p, l u w T y l + + T w - T l

(2)

여기서, A₁은 벽면에서 기포에 영향을 받는 면적의 비율을 의미하며 A₁=1-A₂로 정의된다. 그리고 ρ_l은 액체의 밀도, c_p,l은 액체의 비열, u_w은 액체의 마찰속도, T_w는 벽면 온도, T_l은 액체의 온도, $y l +$ 는 벽면에 인접한 첫 번째 격자의 노드까지 액체의 무차원 거리를 의미한다. 그리고 $T yl + +$ 는 각 노드에서 $y l +$ 에 대한 무차원 온도를 나타낸다.

급속냉각에 의한 열전달은 벽면에서 기포 핵이 생성되어 기포의 성장이 충분이 이루어지게 되면 기포는 벽면을 이탈하게 되는데 이때, 기포가 위치한 자리에 액체가 유입되면서 발생된다. 급속냉각에 의한 열전달은 식 (3)과 같이 정의된다.

y l + Q q = A 2 h q T w - T l w A 2 = m i n π d w 2 N a, 1 T l w = T w - T y l + w + T y l + + T w - T l

(3)

여기서 d_w는 기포의 이탈직경(bubble departure diameter), Na는 핵 사이트 밀도(nucleation site density)를 의미한다. 식 (2)와 식 (3)에서 보는 바와 같이 벽 함수를 포함하는 무차원 온도를 사용하기 때문에 벽비등 모델의 경우 격자 의존성이 낮게 나타난다.

증발에 의한 열전달은 액체에서 기체로 상변화 되는 과정에서 이루어지며, 식 (4)와 같이 잠열, H_lg와 관련이 있다.

Q e = m ̇ w H 1 g m ̇ w = π d w 3 6 ρ g N a f

(4)

여기서 $m ̇ ω$ 는 증기의 발생률을 의미하며, 증기의 발생률은 기포의 이탈 직경, 핵 사이트 밀도 그리고 기포 이탈 빈도, f에 관한 식으로 표현된다.

이와 같이 열유속 분할 모델은 기포의 이탈 직경, 핵 사이트 밀도 그리고 기포 이탈 빈도 등의 하위 모델을 가지며, 이 세가지 하위 모델이 가장 많은 영향을 끼친다.

기본적으로 CFX에서 사용하는 핵 사이트 밀도는 식 (5)와 같은 Lemmert and Chawla[19]의 상관식을 적용한다.

Na = 210 Δ T sup 1.805

(5)

여기서 ΔT_sup는 T_w-T_sat로서 과열도를 나타낸다.

Basu et al.[18]은 1대기압에서 수행한 실험 결과에 따라서 핵 사이트 밀도를 예측하는 상관식을 식 (6)과 같이 제안하였다.

Na = 0.34 × 104 1 - cos θ T sup 2.0 for Δ T onb < Δ T sup < 15 K Na = 0.34 1 - cos θ T sup 5.3 for Δ T sup ≥ 15 K

(6)

여기서 θ는 기포와 벽면의 접촉각을 의미하며, T_onb는 핵 비등이 시작되는 온도를 뜻한다.

Koncar et al. [23]은 Lemmert and Chawla[19]의 핵 사이트 밀도에 관한 상관식을 일부 수정하여 식 (7)과 같이 제안하였다.

Na = 185 Δ T sup 1.805

(7)

기포의 이탈 직경은 CFX에서는 기본적으로 식 (8)과 같이 Tolubinskiy and Kostanchuk[24]의 모델을 사용한다. 이 모델은 기포의 이탈직경을 과냉도(ΔT_sub=T_sat-T_liquid)의 관한 함수로 계산한다.

d w = min 6 mm exp - Δ T su b 45 K, 1.4 mm

(8)

1대기압 부근의 저압영역에서 주로 사용되는[11][20] 기포 이탈 직경에 대한 상관식은 Kocamustafaogullari and Ishii[16]가 제안한 상관식으로 식 (9)와 같다.

d w = 2.5 × 10 - 5 ρ l - ρ g ρ l 0.9 θ σ g ρ l - ρ g

(9)

여기서 σ는 표면장력을 의미한다.

CFX에서 기본적으로 사용되는 기포의 이탈 빈도, f는 Cole[25]의 상관식을 사용하며, 식 (10)과 같다.

f = 4 g ρ l - ρ g 3 d w ρ l

(10)

그 외에 자주 사용되는 기포 이탈 빈도의 상관식은 Stephan[26]의 상관식과 Kocamustafaogullari and Ishii[16]의 상관식이 있으며, 각각 식 (11)과 식 (12)와 같이 표현된다.

f = 1 π g 2 d w 1 + 4 σ d w 2 ρ l g 0.5

(11)

f = 1.18 d w σ g ρ l - ρ g ρ l 2 0.25

(12)

2.2 해석 조건

2.2.1 경계 조건

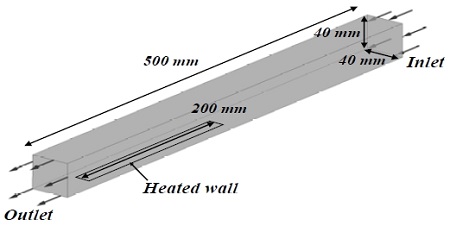
본 연구에서는 Maurus et al.[21]의 실험값과 수치해석 결과를 비교하였으며, 실험 및 수치해석에 사용된 시험부의 형상은 Figure 1과 같다. 시험부는 길이 500mm, 폭과 넓이가 40mm인 정사각 채널로 구성되며, 시험부의 바닥면에는 히터에 의해 열이 공급된다. 히터는 길이 200mm 그리고 폭 15mm의 크기로 입구에서부터 250mm 지점에 설치된다. 수치해석의 경계 조건은 실험값에 맞추어 Table 1과 같이 설정하였다.

Figure 1:

Geometry of test section

Table 1:

Boundary conditions

난류는 SST(shear stress transport) 모델을 사용하였으며, 액체와 기체간의 운동량 전달을 계산하기 위한 모델은 Table 2에서 정리한 것과 같이 CFX에서 기본적으로 제공하는 모델을 사용하였다. Krepper[1]에 따르면 non-drag force는 축방향(유동방향)의 기공률 분포에는 거의 영향을 미치지 않으며, 반경방향의 기공률 분포에 영향을 주는 것으로 나타났다. 따라서 운동량 전달에 관한 모델은 본 연구의 결과에 크게 영향을 미치지 않는 것으로 간주하였다.

Table 2:

Momentum transfer model

2.2.2 격자 의존성 검토

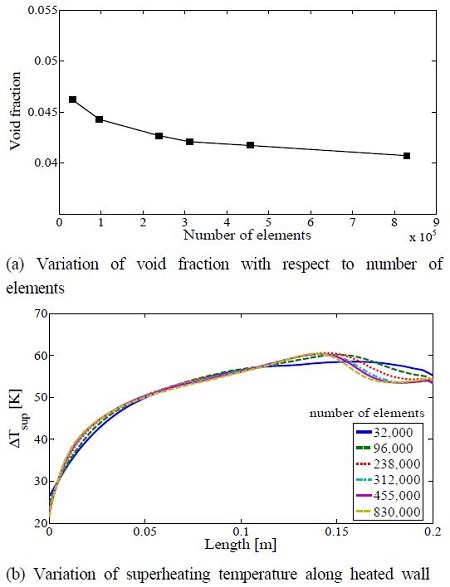
격자는 Hexahedral 격자계로 구성되었으며, 격자 의존성검토를 위한 격자수는 32,000~830,000개로 설정하였다. Figure 2 (a)는 질량유속 250kg/m²s, 열유속 0.63MW/m² 일 때, 격자수에 따른 가열면에서의 평균 기공률을 나타낸 것 이다. 기공률은 약 0.041에서 0.046사이에 있었으며, 격자수 23만개이상에서는 기공률의 변화가 작게 나타났으며, 23만개에서 83만개로 격자수를 약 4배 증가시켰을 때 기공률은 0.043에서 0.041로 5% 이내의 차이가 발생하였다. Figure 2 (b)는 격자수에 따른 가열면의 중심부에서 축방향에 따른 과열도를 나타낸 것이다. 가장 성근 격자인 32,000개의 격자의 경우 하류 측에서 다른 조밀한 격자의 계산과 비교해서 과열도의 경향이 다르게 나타나며, 이것은 과열도 예측의 정확성이 낮은 것으로 판단된다. 312,000개 이상의 격자에서는 과열도 예측에 큰 차이가 없는 것으로 나타났다. 따라서 나머지 모든 조건에서는 312,000개를 기준으로 계산을 수행하였다.

Figure 2:

Mesh independence test with respect to number of mesh elements

3. 결과 및 고찰

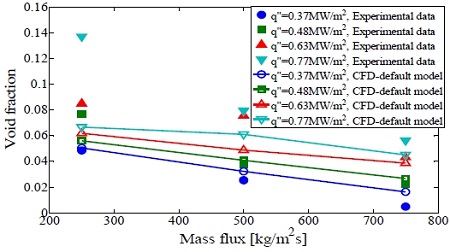
Figure 3은 질량유속과 열유속 변화에 따라서 가열면에서의 기공률의 상한 값을 나타낸 것으로서, Maurus[21]의 실험값과 수치해석 결과를 비교하여 나타낸 것이다. 수치해석은 CFX 13.0에 내장된 Lemmert and Chawla[19], Tolubinskiy and Kostanchuk[24] 그리고 Cole[25]의 상관식을 사용하였다. 가열면에서의 기공률의 상한 값은 열유속의 증가와 질량유속의 감소에 따라서 증가하였다. 하지만 기본 모델을 사용한 수치해석 결과는 기공률을 실험값과 비교해서 열유속 증가에 따른 기공률의 증가 경향을 잘 예측하지 못하는 것으로 나타났다. 상용코드에서 제공하는 기본적인 모델은 과냉각 비등 현상을 정확하게 예측할 수 없는 것을 확인하였다. 기본 모델의 경우 대부분 고압에서 수행된 실험 결과를 기반으로 개발된 상관식을 적용하므로, 저압조건에서의 과냉각 비등 현상을 모사하기 위해서는 그 조건에 적합한 상관식을 적용할 필요가 있다. 따라서 본 연구에서는 우선 기포 이탈 직경은 기본 모델인 Tolubinskiy and Kostanchuk[24]의 상관식으로 고정하고 2장에서 언급한 핵 사이트 밀도와 기포 이탈 빈도의 조합으로 수치해석을 수행하였다. 핵 사이트 밀도는 Basu et al.[18]과Koncar[23]의 상관식을 사용하였으며, 기포 이탈 빈도는 Kocamustafaogullari and Ishii[16]와 Stephan[26]의 상관식을 사용하였다.

Figure 3:

Comparisons between the experimental data and default models

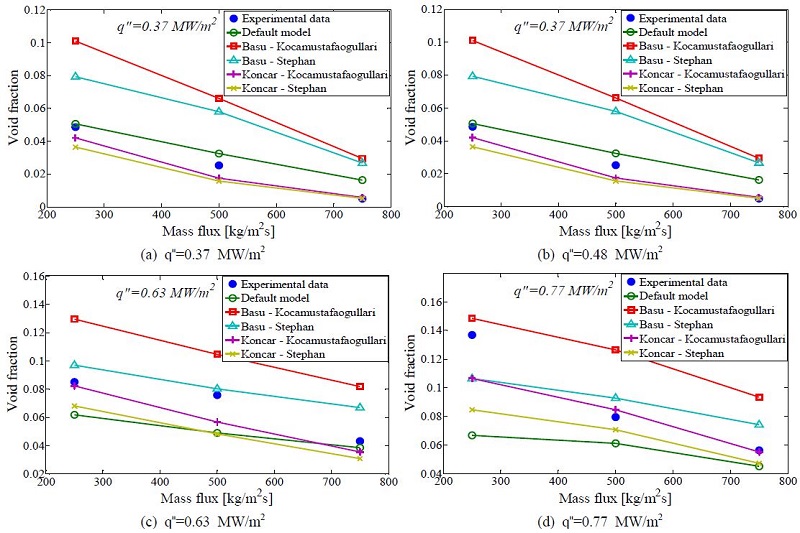
핵 사이트 밀도와 기포 이탈 빈도의 상관식 조합에 따른 기공률 변화는 Figure 4에 나타내었다. 수치해석 결과에 따르면 기공률은 기포 이탈 빈도에 비해서 핵 사이트 밀도에 적용된 상관식의 영향을 더 받는 것으로 나타났다. 핵 사이트 밀도에 Basu[23]의 상관식을 적용한 경우 전반적으로 기공률을 높게 예측하였다. 낮은 열유속(q"=0.37, 0.48 MW/m²)에서 기본 모델은 실험값을 근사하게 예측하는 것으로 보이나, 열유속이 증가할수록 기본 모델의 예측 정확성은 감소하였다. 전체적으로 Basu-Kocamustafaogullari의 모델이 전 열유속 범위 내에서 실험값을 가장 근사하게 예측하는 것으로 나타났다. 하지만 높은 열유속(q"=0.77 MW/m²)에서 낮은 질량유속(G=250kg/m²s)일 때, 실험값에서 높게 나타나는 기공률을 예측하지 못하였다. 이것은 벽비등 모델이 낮은 기공률일 때 나타나는 기포류 유동을 모사하기 적합한 모델로서 기공률이 급격하게 상승하는 지점에서는 예측의 정확성이 감소되는 것으로 판단된다. 각 모델들의 기공률 예측의 정확성은 식 (13)과 같이 정의되는 MAE(mean absolute error)를 사용하여 비교하였으며, 그 결과는 Table 3에 나타내었다.

Figure 4:

Variation of void fraction with respect to mass flux

MAE % = 1 N ∑ α pred - α exp α exp × 100

(13)

Table 3:

Mean absolute error

Koncar-Kocamustafaogullari 모델이 MAE 16.89% 내에서 실험 데이터를 가장 잘 예측하였으며, 핵 사이트 밀도에 Basu[18]의 상관식을 적용한 경우 기본 모델보다 예측의 정확성이 낮게 나타났다.

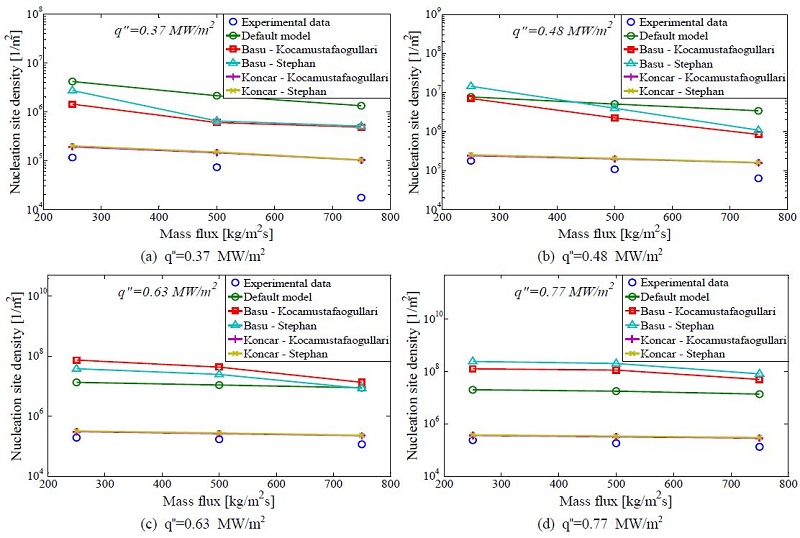
Figure 5는 각 모델별 열유속 및 질량유속 변화에 따른 핵 사이트 밀도를 나타낸 것이다. 수치해석 결과에 따르면 Basu 모델과 기본 모델은 실험값에 비해서 핵 사이트 밀도를 높게 예측하였다. Koncar 모델은 실험값에 비해서 다소 높게 예측하였지만 Basu 모델 및 기본 모델과 비교하면 핵 사이트 밀도를 비교적 잘 예측하는 것으로 나타났다.

Figure 5:

Variation of nucleation site density with respect to mass flux

4. 결 론

본 연구에서는 기존의 실험 자료를 바탕으로 저압에서의 과냉각 비등 현상에 대한 CFD 수치해석에 관한 연구를 수행하였으며, 다음과 같은 결론을 얻었다.

1. 고압에서의 실험 자료를 기반으로 개발된 상용코드의 기본적인 모델은 저압에서의 과냉각 비등 현상을 정확하게 예측할 수 없었다.
2. 핵 사이트 밀도에 관한 상관식으로는 Basu et al.[18]과 Koncar et al.[23]의 상관식을 적용하였으며, 기포 이탈 빈도에 관한 상관식으로는 Kocamustafaogullari and Ishii[16]와 Stephan[26]의 상관식을 적용하여 수치해석을 수행하였다. 수치해석 결과는 실험결과와 비교하였으며, 그 결과 Koncar-Kocamustafaogullari 모델이 실험에서 얻어진 기공률을 MAE 16.89% 내에서 다른 모델들에 비해서 가장 잘 예측하였다.
3. Basu et al.[18]의 상관식을 적용한 모델은 핵 사이트 밀도를 실험값에 비해서 높게 예측하였으며, Koncar et al.[23]의 상관식을 적용한 모델이 핵 사이트 밀도를 실험값에 비교적 근사하게 예측하였다.
4. 핵 사이트 밀도와 기포 이탈 빈도에 적합한 상관식을 적용함으로써 저압에서의 과냉각 비등 현상에 대한 정확성을 높일 수 있었으나, 전체적인 예측에는 미흡한 것으로 판단된다. 따라서 저압에서의 과냉각 비등 현상을 보다 정확하게 예측할 수 있는 모델의 지속적인 개발이 요구된다.

References

E. Krepper, B. Koncar, and Y. Egorov, “CFD modelling of subcooled boiling-concept, validation and application to fuel assembly design”, Nuclear Engineering and Design, 237(7), p716-731, (2007). [https://doi.org/10.1016/j.nucengdes.2006.10.023]
W. K. In, C. H. Shin, and T. H. Chun, “Near-wall grid dependency of CFD simulation for a subcooled boiling flow using wall boiling model”, Journal of Computational Fluids Engineering, 15(3), p24-31, (2010), (in Korean).
Y. S. Choi, and T. W. Lim, “Heat transfer characteristics and flow pattern investigation in micro-channels during two-phase flow boiling”, Journal of the Korean Society of Marine Engineering, 39(7), p696-701, (2015), (in Korean). [https://doi.org/10.5916/jkosme.2015.39.7.696]
H. Anglart, and O. Nylund, “CFD application to prediction of void distribution in two-phase bubbly flows in rod bundles”, Nuclear Engineering and Design, 163(1-2), p81-98, (1996). [https://doi.org/10.1016/0029-5493(95)01160-9]
R. Zhuan, and W. Wang, “Flow pattern of boiling in micro-channel by numerical simulation”, International Journal of Heat and Mass Transfer, 55(5-6), p1741-1753, (2012). [https://doi.org/10.1016/j.ijheatmasstransfer.2011.11.029]
B. U. Bae, B. J. Yun, H. Y. Yoon, C. H. Song, and G. C. Park, “Analysis of subcooled boiling flow with one-group interfacial area transport equation and bubble lift-off model”, Nuclear Engineering and Design, 240(9), p2281-2294, (2010). [https://doi.org/10.1016/j.nucengdes.2010.04.001]
Y. Y. Jiang, H. Osada, M. Inagaki, and N. Horinouchi, “Dynamic modeling on bubble growth, detachment and heat transfer for hybrid-scheme computations of nucleate boiling”, International Journal of Heat and Mass Transfer, 56(1-2), p640-652, (2013). [https://doi.org/10.1016/j.ijheatmasstransfer.2012.09.006]
D. Prabhudharwadkar, M. A. Lopez-de-Bertodano, T. Hibiki, and J. R. Buchanan Jr, “Assessment of subcooled boiling wall boundary correlations for two-fluid model CFD”, International Journal of Heat and Mass Transfer, 79, p602-617, (2014). [https://doi.org/10.1016/j.ijheatmasstransfer.2014.08.040]
G. G. Bartolomej, and V. M. Chanturiya, “Experimental study of true void fraction when boiling subcooled water in vertical tubes”, Thermal Engineering, 14(2), p123-128, (1967).
E. Chen, Y. Li, and X. Cheng, “CFD simulation of upward subcooled boiling flow of refrigerant-113 using the two-fluid model”, Applied Thermal Engineering, 29(11-12), p2508-2517, (2009). [https://doi.org/10.1016/j.applthermaleng.2008.12.022]
S. C. P. Cheung, S. Vahaji, G. H. Yeoh, and J. Y. Tu, “Modeling subcooled flow boiling in vertical channels at low pressures – part 1: assessment of empirical correlations”, International Journal of Heat and Mass Transfer, 75, p736-753, (2014). [https://doi.org/10.1016/j.ijheatmasstransfer.2014.03.016]
O. Zeitoun, and M. Shoukri, “Bubble behavior and mean diameter in subcooled flow boiling”, Journal of Heat Transfer, 118(1), p110-116, (1996). [https://doi.org/10.1115/1.2824023]
B. J. Yun, G. C. Park, C. H. Song, and M. K. Chung, “Measurements of local two-phase flow parameters in a boiling flow channel”, Proceedings of the OECD/CSNI Specialist Meeting on Advanced Instrumentation and Measurement Techniques, p243-265, (1997).
T. H. Lee, G. C. Park, and D. J. Lee, “Local flow characteristics of subcooled boiling flow of water in a vertical concentric annulus”, International Journal of Multiphase Flow, 28(8), p1351-1368, (2002). [https://doi.org/10.1016/S0301-9322(02)00026-5]
H. C. Unal, “Maximum bubble diameter, maximum bubble-growth time and bubble-growth rate during the subcooled nucleate flow boiling of water up to 17.7 MN/m2”, International Journal of Heat and Mass Transfer, 19(6), p643-649, (1976). [https://doi.org/10.1016/0017-9310(76)90047-8]
G. Kocamustafaogullari, and M. Ishii, “Interfacial area and nucleation site density in boiling systems”, International Journal of Heat and Mass Transfer, 26(9), p1377-1387, (1983). [https://doi.org/10.1016/S0017-9310(83)80069-6]
W. Fritz, “Maximum volume of vapor bubbles”, Physikalische Zeitschrift, 36, p379-384, (1935).
N. Basu, G. R. Warrier, and V. K. Dhir, “Onset of nucleate boiling and active nucleation site density during subcooled flow boiling”, Journal of Heat Transfer, 124(4), p717-728, (2002). [https://doi.org/10.1115/1.1471522]
M. Lemmert, and J. Chawla, Influence of Flow Velocity on Surface Boiling Heat Transfer Coefficient, Heat Transfer in Boiling, E. Hahne Ed, and U. Grigull, Hemisphere Publishing Corporation, p237-247, (1977). [https://doi.org/10.1080/01457632.2013.833053]
H. T. Kim, H. K. Park, Y. T. Kim, K, H. Bang, and J. S. Suh, “Flow boiling in an inclined channel with downward-facing heated upper wall”, Heat Transfer Engineering, 35(5), p492-500, (2014). [https://doi.org/10.1080/01457632.2013.833053]
R. Maurus, V. Ilchenko, and T. Sattelmayer, “Study of the bubble characteristics and the local void fraction in subcooled flow boiling using digital imaging and analysing techniques”, Experimental Thermal and Fluid Science, 26(2-45), p147-155, (2002). [https://doi.org/10.1016/S0894-1777(02)00121-8]
N. Kurul, and M. Z. Podowski, “Multi-dimensional effects in forced convection subcooled boiling”, Proceedings of the Ninth Heat Transfer Conference, 2, p21-26, (1990).
B. Koncar, I. Kljenak, and B. Mavko, “Modelling of local two-phase flow parameters in upward subcooled flow boiling at low pressure”, International Journal of Heat and Mass Transfer, 47(6-7), p1499-1513, (2004). [https://doi.org/10.1016/j.ijheatmasstransfer.2003.09.021]
V. Tolubinsky, and D. Kostanchuk, “Vapour bubbles growth rate and heat transfer intensity at subcooled water boiling”, Proceedings of the Fourth International Heat Transfer Conference, 5, Paper No. B-2.8, (1970).
R. Cole, “A photographic study of pool boiling in the region of the critical heat flux”, AIChE Journal, 6(4), p533-538, (1960). [https://doi.org/10.1002/aic.690060405]
K. Stephan, Heat Transfer in Condensation and Boiling, Springer-Verlag, (1992). [https://doi.org/10.1007/978-3-642-52457-8]

Parameter	Value
mass flux at inlet	250, 500, 750 [kg/m²s]
heat flux at heated wall	0.37, 0.48, 0.63, 0.77 [MW/m²]
pressure at outlet	0.11 [MPa]
Δt_sub at inlet	20 [K]

Model		Correlation
drag force		Ishii Zuber
non-drag force	lift force	Tomiyama
	wall lubrication force	Antal
	turbulent dispersion force	Favre averaged drag force

Model	MAE(%)
Default model	41.20
Basu-Kocamustafaogullari	119.76
Basu-Stephan	84.71
Koncar-Kocamustafaogullari	16.89
Koncar-Stephan	26.12