한 면에 ∧/∨형 리브가 있는 2벽면 수축 사각채널의 열전달 증가

Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
양 벽면이 수축되는 채널에서 ∨/∧형 리브의 각도가 열전달에 미치는 효과를 실험적으로 조사하였다. 한 벽면에만 설치된 ∨/∧형 리브의 충돌 각은 각각 30°, 45°, 60° 그리고 90°이다. 리브의 높이(e)는 10 mm 그리고 리브 간격(p)과 높이(e)비는 10으로 제작하였다. 길이가 1,000 mm인 시험 부는 입구의 단면적은 100 mm x 100 mm, 출구는 50 mm x 100 mm으로 제작하였다. 레이놀즈수가 22,000에서 75,000까지의 범위에서 실험을 수행하였다. 연구결과 전체적으로 레이놀즈 수가 높을수록 누셀트 수가 컸고, ∧형 45° 리브가 가장 누셀트 수가 컸다.
Abstract
The effect of the rib angle-of-attack on heat transfer in the convergent channel with ∨/∧-shaped ribs was examined experimentally. Four differently angled ribs (a = 30°, 45°, 60°, and 90°) were placed to only the one sided wall. The ribbed wall was manufactured with a fixed rib height (e) of 10 mm and rib spacing (p)-to-height (e) ratio of 10. The convergent channel had a length of 1,000 mm and a cross-sectional areas of 100 mm×100 mm at inlet and 50 mm×100 mm at exit. The measurement was conducted for the Reynolds numbers ranging from 22,000 to 75,000. The results show that the Nusselt number is generally higher at higher Reynolds number and that an angle-of-attack of 45° at the ∧-shaped rib produces the greatest Nusselt number.
Keywords:
∨/∧-shaped rib, Convergent rectangular channel, Heat transfer, Total friction factor, Rib angle-of-attack키워드:
∨/∧형 리브, 2 벽면 수축채널, 열전달, 전 마찰계수, 리브 충돌 각1. 서 론
가스터빈 엔진의 출력은 높은 입구온도와 관련 있기 때문에 가스터빈 입구 온도는 계속 증가되었으며 현재는 가스터빈 재질의 허용 한계를 훨씬 초과한다. 따라서 다양한 냉각 기술은 가스 터빈 엔진 연구에서 중요한 요소로 신뢰성 및 내구성을 향상시키기 위해 많은 연구들이 진행 중이다. 이 중 난류 촉진체인 리브(rib)의 설치는 덕트 내에서 열전달을 향상시키므로 가스 터빈 블레이드 냉각에 지속적으로 사용되어져 왔다. Ahn et al. [1]은 리브를 한면, 양면, 그리고 사면 모두에 각각 설치한 정사각 직선채널의 열전달과 마찰계수에 관한 연구를 수행하였다. Han et al. [2]은 직선 정사각 채널의 실험에서 리브 충돌각 60°~ 75°에서 열전달계수가 최대값을 가지며, 일정한 유체이송동력 조건에선 충돌각이 30°~ 45°일 때 최대의 열전달 향상효과가 있었음을 보였다.
Momin et al. [3]은 직선 채널에서 30°, 45°, 60° 그리고 90° ∨형 리브의 열전달을 비교한 결과 60° ∨형 리브 채널이 가장 높은 누셀트수를 나타내었다. Han et al. [4]은 직선 채널에서 ∧형 리브와 ∨형 리브의 형상 변화와 각도변화를 조사한 결과 ∧와 ∨형 리브가 평행 경사형 리브보다 열전달 성능이 우수함을 보였다.
그러나 가스터빈 블레이드의 냉각 통로는 에어호일(airfoil)형으로 통로의 횡단면의 길이는 통로 바닥에서 천정에 이르는 높이에 따라 변하므로 확대와 수축채널에 해당된다. 확대와 수축채널에 관한 연구로는 Wang et al. [5]은 리브가 설치된 확대와 수축 사각 채널의 입구 영역에서 횡단 면적의 변화가 국부와 채널 평균 열전달에 미치는 영향을 측정한 결과 횡단 면적의 변화는 채널 평균 열전달에 큰 영향을 준다는 것을 입증하였다. Lee et al. [6]은 4벽면 중 2벽면만 확대되는 채널에서 30°, 45°, 60° 그리고 90° 충돌각의 리브가 열전달과 마찰계수에 미치는 효과를 실험적으로 조사하였다.
국내에서는 이와 안 [7]이 4벽면 확대채널에서 리브 충돌각이 30°, 45°, 60°, 그리고 90°인 리브가 설치된 경우에 대한 국부 열전달과 마찰계수를 측정한 결과 45° 리브 충돌각이 가장 우수한 열전달 성능을 보였다.
이에 본 연구의 목적은 양 벽면이 수축되는 사각 채널내 한 면에 설치된 ∨/∧형 리브에서 30°, 45°, 그리고 60°인 리브 충돌각이 열전달과 마찰계수에 미치는 효과를 실험적으로 조사하여 최적 설계를 구하는데 있다.
2. 장치 및 방법
실험 장치를 도식적으로 나타낸 그림이 Figure 1이다. 작동 유체로는 실내 공기를 사용하였고 출구 측에 설치 한 송풍기를 통해 시험부 입구로 유입되게 하였다. 전체 채널의 길이는 4,000 mm이고 시험부의 입구와 출구는 외부의 영향을 최소화하기 위해 투명 폴리카포나이트 각각 2,000 mm와 1,000 mm를 설치하였다. 시험부 입구는 100 mm x 100 mm 출구는 50 mm x 100 mm으로 제작하였고 입구와 축구의 수력직경 비(Dho/Dhi)는 0.67이다.
시험부 상·하 벽면은 열전도성이 높은 구리판을 여러 영역으로 나누는 구리판법(copper plate method)을 이용하여 10개의 영역으로 구분 하여 길이 방향 열전도를 최소화 하였다. 매 영역은 100 mm x 100 mm x 20 mm(t)의 구리판을 10 개 설치하였고 각 영역에 설치된 구리판 사이의 열전도를 방지하기 위해 0.5 mm 두께의 고무 가스켓을 설치하였다.
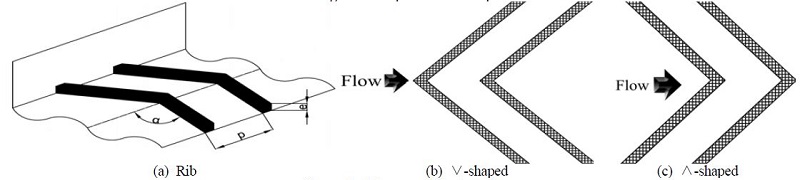
리브는 한면에만 설치하고 리브가 설치된 벽은 Figure 2 (a)와 같이 10 mm x 10 mm(t)의 리브를 연속적으로 배치되었다. 리브의 충돌 각은 30°, 45° 그리고 60°로 변화를 주었고 리브의 피치(p)는 10으로 고정하였다. 주유동의 방향에 따라 (b)와 (c)와 같이 ∨/∧형 리브로 구분하였다.
입구와 출구측의 구리판을 제외하고 각 구리판에 T형 구리-콘스탄탄 열전대를 동판의 중간 높이에 50 mm(입구와 출구는 75 mm) 간격으로 각 영역에 2개씩 설치하였다. 구리판 밑에는 0.1 mm 두께의 실리콘 포일 히터, 0.5 mm 두께의 마이카, 50 mm두께의 송판, 20 mm 두께의 유리섬유를 설치하여 단열하였다[7]. 단위면적 당의 열 손실(ql)은 아래와 같이 계산된다.
| (1) |
여기서 T∞는 주위온도, ∆y1과 k1는 운모의 두께와 열전도도, ∆y2과 k2는 송판의 두께와 열전도도, ∆y3과 k3는 유리 섬유의 두께와 열전도도, 그리고 h1는 채널 주위의 자연 대류 열전달 계수이다. 모든 경우 열손실은 5.8%이내였다. 본 연구에서는 단상 교류 전원을 사용하였으며, 히터에서 공급되는 열전달율(Q-Ql)은 아래의 대류 열전달에 의해 점검하였다.
| (2) |
여기서 은 공기 질량, Tbo와 Tbi는 시험 부 출구와 입구의 체적 평균 온도이다. 채널 유동의 전(total) 마찰 계수는 채널 확대에 의한 동압 성분과 정압 성분을 합한 압력 강하(∆PT)를 이용하여 식 (4)에 의해 구했다.
| (3) |
| (4) |
여기서 Pi와 Po는 각각 시험부 입구와 출구의 정압이다. 누셀트 수(Nu)는 아래와 같이 정의하였다.
| (5) |
Dh은 시험부 채널평균 수력 직경이고 kair은 공기의 열전도도이며 h는 채널평균 대류 열전달 계수이다. 압력측정에 사용된 디지털 마노메터의 측정오차는 19.99 mmH2O의 정압에서 0.01 mmH2O이내이고 열전대의 온도측정 오차는 0.1°C이었다.
불확실성은 Kline과 McClintock[8]의 방법으로 실시하였고 누셀트 수와 마찰계수는 각각 최대 11 %와 12%이었다
3. 실험결과 및 고찰
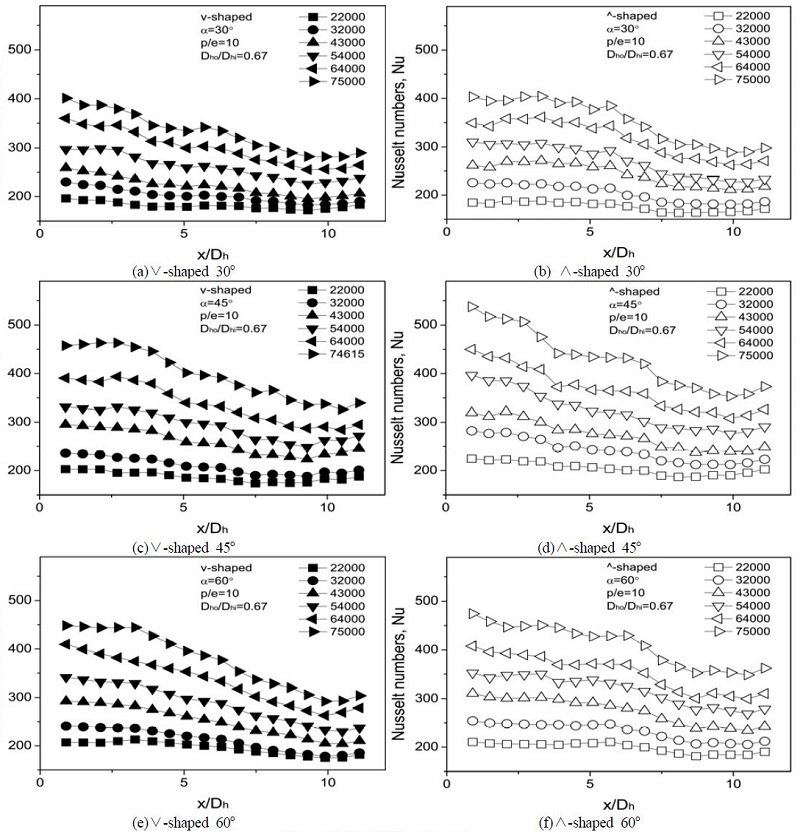
Figure 3은 거리에 따른 국부 누셀트수를 보여준다. ∧형 리브와 ∨형 리브 모두 길이방향 거리에 따라 감소하였다. 이는 가열된 채널유동의 경우 채널 입구에서는 차가운 유체의 냉각작용으로 가열벽면의 온도와 유체체적 평균온도와의 차이가 작기 때문이다. 축방향 거리에 따라 감소되는 영역이 직선채널[1] 보다 훨씬 컸다. 그 이유는 채널 수축으로 인한 유속 증가로 길이방향 거리에 따라 유체 체적 평균온도의 증가는 벽면 온도의 증가에 비해 작기 때문으로 사료된다. 이러한 현상은 Lee et al. [10]에서도 나타났다.
리브 충돌각(α)이 45°와 60°의 ∧형 리브에서는 높은 레이놀즈 수[(ubDh/ν) = 75,000]의 경우 누셀트 수가 입구 영역에서 컸다가 급하게 강하하였다. 이는 가열벽면의 열전대가 채널바닥 중심선에 있고 채널 시험부로 유입되는 유체를 ∧형 리브가 바닥의 중심부로 모이게 하기 때문으로 사료된다.
모든 경우 레이놀즈수가 증가할수록 높은 국부 누셀트 수를 나타내었다. 이는 레이놀즈수가 증가 할수록 유속의 증가로 인하여 난류 혼합이 증가하였기 때문으로 사료된다. 모든 경우 시험부 출구에서 누셀트 수가 증가 하였다. 이는 출구근처에 설치된 구리판의 열전도 손실 때문이라 판단된다.
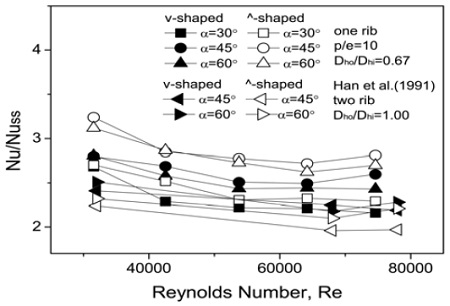
Figure 4는 레이놀즈 수에 따른 Nu/Nuss의 분포를 나타낸다. 매끈한 직선 원형관 채널의 누셀트 수(Nuss)에 대한 상관 관계식은 아래의 Dittus-Boelter[9]식 (6)을 이용하였다.
| (6) |
비교를 위해 직선채널에서 양측벽면에 ∨와⋀형 리브가 설치된 Han et al. [4]의 결과를 포함하였다. 본 연구의 결과보다 무차원 누셀트수가 작았다. 이는 1) 본 연구의 경우 길이방향에 따라 채널이 수축되는 단면적으로 인하여 채널 중심부 유동(core flow)이 가열 벽면에 가까워지고, 2) Han et al. [4]의 경우 리브 높이(e)/채널 수력직경(Dh)의 비가 0.0625로 본 연구보다 작기 때문이라 사료된다.
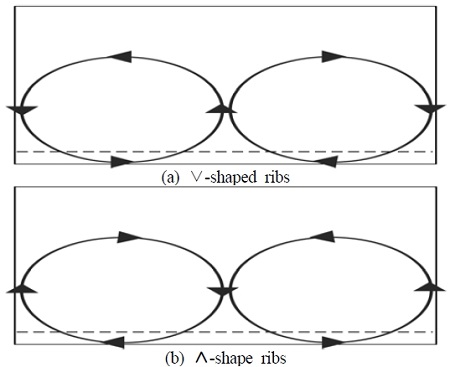
⋀형 45°리브가 가장 큰 값을 나타냈고 ∨형30°형 리브가 가장 작았다. ⋀형 리브 채널이 ∨형 리브 채널보다 대체로 크게 나타났다. 이는 직선채널에 관한 Han et al. [4]의 결과와 반대된다. 이는 채널이 수축함에 따라 유동 단면적 폭이 좁아져 반대측 벽면에서 발생하는 2차유동이 발생하여 Figure 5와 같이 채널 중심부로 발생하는 스월유동이 크게 발생하기 때문이다. ⋀형 45°리브가 가장 높은 누셀트 수를 보였으며 ⋀형 리브 채널은 원형관에 비해 약 2.8 ~ 3.8 배 무차원 누셀트 수가 크고 ∨형 리브 채널에서는 약 2.4 ~ 3.6 배 무차원 누셀트 수가 크게 나타났다.
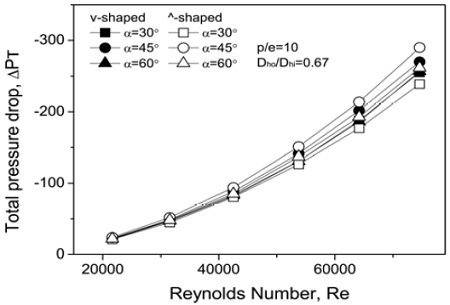
Figure 6은 ∨와 ⋀형 리브각도에 따른 식 (3)에 의한 전압강하를 나타낸다. 모든 채널에서 음(-)의 값을 나타냈다. 이는 채널이 수축함에 따라 유속 증가로 인한 동압과 정압강하 때문으로 사료된다. 수축이나 확대 채널의 경우 정압과 동압이 동시에 발생하며 정압과 동압은 채널의 수축율과 확대율과 리브에 따라 전압이 정(+), 영(0), 그리고 부(-)의 값이 될 수 있다. 그러므로 채널의 수축과 확대율과 벽면 리브의 형상에 따라 전압이 영(0)이 되는(마찰계수가 없는) 채널의 설계가 가능하다. 이러한 설계를 위해서는 추가 적인 연구가 요구된다.
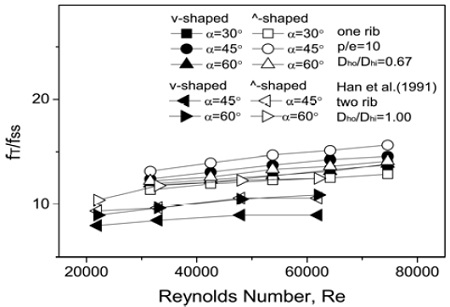
Figure 7은 레이놀즈 수에 따른 fT/fss의 분포를 나타낸다. 아래첨자 ss는 매끈한 원관에 관한 Blasius[11]식 (7)에 의한 값이다.
| (7) |
비교를 위해 직선채널에서 양측벽면에 ∨와 ⋀형 리브가 설치된 Han et al. [4]의 결과를 포함하였다. ∧형 리브채널에서 45°리브 충돌각의 경우 9∼13% 높은 마찰계수를 나타내었다. 이는 유동 방향거리에 따라 수축되는 단면에서 Figure 5와 같이 리브경사에 따른 이차유동이 발생하는데 리브가 설치된 면을 바닥면으로 봤을 때 ∧형 리브의 경우 리브의 경사에 따라 이동한 유체가 채널 중심부에서 상승하는 스월 때문이며 이는 Han et al. [4]의 직선채널 연구결과와 유사하다.
4. 결 론
양 벽면이 수축되는 채널에서에서 한 면에 설치된 ∨/∧형 리브가 열전달과 마찰계수에 미치는 효과에 관한 연구 결과 다음과 같은 결론을 얻었다.
- 1) ∧형 리브와 ∨형 리브 모두 출구 측에 가까울수록 국부 누셀트 수가 증가하였다.
- 2) ⋀형 45°리브가 가장 높은 누셀트 수를 보였으며 ⋀형 리브 채널은 원형관에 비해 약 2.8 ~ 3.8 배 무차원 누셀트 수가 크고 ∨형 리브 채널에서는 약 2.4 ~ 3.6 배 무차원 누셀트 수가 크게 나타났다.
- 3) ∧형 리브가 ∨형 리브보다 높은 마찰계수를 나타내었다.
References
-
S. W. Ahn, H. K. Kang, S. T. Bae, and D. H. Lee, “Heat transfer and friction factor in a square channel with one, two, and four ribbed walls”, ASME Journal of Turbomachinery, 130, 034501-5 p1-5, (2008).
[https://doi.org/10.1115/1.2775488]

-
J. C. Han, S. Ou, J. S. Park, and C. Lei, “Augmented heat transfer in rectangular channels of narrow aspect ratios with rib turbulators”, International Journal of Heat and Mass Transfer, 32(9), p1619-1630, (1989).
[https://doi.org/10.1016/0017-9310(89)90044-6]

-
A. E. Momin, J. Saini, and S. Solanki, “Heat transfer and friction in solar air heater duct with V-shaped rib roughness on absorber plate”, International Journal of Heat and Mass Transfer, 45(16), p3383-3396, (2002).
[https://doi.org/10.1016/S0017-9310(02)00046-7]

-
J. C. Han, Y. Zhang, and C. Lee, “Augmented heat transfer in square channels with parallel, crossed, and V-shaped angled ribs”, ASME Journal of Heat Transfer, 113(3), p590-596, (1991).
[https://doi.org/10.1115/1.2910606]

-
B. Wang, W. Q. Tao, Q. W. Wang, and T. T. Wong, “Experimental study of developing turbulent flow and heat transfer in ribbed convergent/divergent square ducts”, International Journal of Heat and Fluid Flow, 22(6), p603-613, (2001).
[https://doi.org/10.1016/S0142-727X(01)00127-8]

-
M. S. Lee, S. S. Jeong, S. W. Ahn, and J. C. Han, “Effects of angled ribs on turbulent heat transfer and friction factors in a rectangular divergent channel”, International Journal of Thermal Sciences, 84, p1-8, (2014).
[https://doi.org/10.1016/j.ijthermalsci.2014.04.010]

-
M. S. Lee, and S. W. Ahn, “Effects of rib angles on heat transfer in a divergent square channel with ribs on one wall”, Journal of the Korean Society of Marine Engineering, 39(6), p609-613, (2015).
[https://doi.org/10.5916/jkosme.2015.39.6.609]

- S. J. Kline, and F. A. McClintock, “Describing uncertainty in single sample experiments”, Mechanical Engineering, 75, p3-8, (1953).
- F. W. Dittus, and L. M. K. Boelter, “Heat transfer in automobile radiators of the tubular type”, University of California (Berkeley), Publication of Engineering, 2, p443, (1930).
-
M. S. Lee, S. S. Jeong, S. W. Ahn, and J. C. Han, “Turbulent heat transfer and friction in rectangular convergent/divergent channels with ribs”, AIAA Journal of Thermophysics and Heat Transfer, 27(4), p660-667, (2013).
[https://doi.org/10.2514/1.T4144]

- F. P. Incorpera, and D. P. Dewitt, Fundamental of Heat and Mass Transfe”, 4th ed, John Willy and Sons, Inc, p424, (1996).