단열층을 가지는 솔라 폰드의 수치해석
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 논문은 단열층을 가지는 솔라폰드의 온도특성을 알아보기 위한 기초 연구이다. 또한, 기존의 단열층을 가지지 않는 경우의 솔라폰드의 온도특성과 비교하였다. 수치해석법은 유한차분법(Finite-Difference Method)를 이용하였으며, 2차원 비정상의 상태를 가정하여 계산하였다. 수치해석을 통해 다음과 같은 결과를 얻었다. 1) 솔라 폰드의 깊이가 깊어지면 폰드의 하부까지 도달하는 일사량이 줄어들기 때문에 온도 상승 효과는 발생하지 않는 것을 확인했다. 2) 동절기에는 토양의 온도가 솔라 폰드 내 물의 온도보다 상대적으로 높아 토양에서 폰드 내로 열이 전달되는 것을 확인할 수 있었다. 3) 단열층을 가지는 솔라폰드의 경우, 태양의 의존율은 83.3%, 보일러의 의존율은 16.7%로 자연에너지의 의존도가 높은 것을 확인할 수 있었다.
Abstract
This paper reports a fundamental study of temperature characteristics of a solar pond with an insulation layer. Further, these characteristics were compared with those of a solar pond without the insulation layer. The governing equation was discretized via finite difference method. The governing equations are two-dimensional unsteady-state second-order partial differential equations. The conclusions of the study are as follows: 1) If the depth of the solar pond was increased, the desired effect of increase in temperature was not produced because the amount of solar insolation received by the bottom of the solar pond decreased. 2) As the temperature of the soil during winter is higher than the temperature of the water in a solar pond, heat was transferred from the soil to the solar pond. 3) For the case of the solar pond with insulation layer, it was estimated that the dependence rate of solar energy was 83.3% and that of the boiler was 16.7%.
Keywords:
Numerical analysis, Solar pond, Insulation layer, Finite Difference Method, Two-dimensional unsteady-state equation키워드:
수치해석, 솔라폰드, 단열층, 유한차분법, 2차원 비정상 방정식1. 서 론
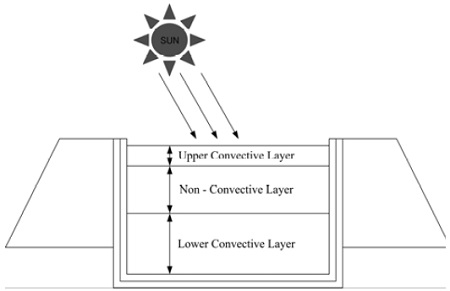
신재생에너지는 무한한 에너지자원으로 그 중에서도 태양에너지를 이용하는 솔라폰드(Solar pond)는 큰 규모로 장시간동안 태양 복사열을 효율적으로 사용할 수 있는 발전 플랜트이다. 솔라폰드의 원리는 연못과 같은 물 웅덩이에 아랫방향으로 갈수록 농도구배를 조성시켜 태양복사열이 태양광선의 파장성분에 따라 선택적으로 흡수시키는 방법으로 단파장 성분은 연못의 하부에 흡수되어 하부 유체의 온도가 상승하고, 농도구배에 의한 대류억제작용으로 고온의 유체가 하부에 머물게 하여 다량의 에너지가 축척되는 것을 이용하는 것이다[1]. 솔라폰드는 Figure 1에 나타나 있는 바와 같이 보통 세 개의 층(Layer)으로 나누어지는데 염도에 따라 자연대류층, 중간층은 밀도가 포화상태에 구배되어 비대류특성을 가지는 층, 맨 아래층은 대류층이다.
맨 아래층으로 도달하는 일사에너지에 의하여 일단 상당한 부피의 온도구배를 형성하게 되지만, 이 온도구배는 소금물의 밀도구배가 안정 되지 않기 때문에 자연대류가 발생하게 되고, 그 위에 위치하는 비대류층은 외부로부터의 열을 차단해 주기 때문에 열저장이 용이하게 된다.
또한, 세 개의 층을 이루게 되는 솔라폰드는 층별로 다른 온도구배를 가지게 된다. 맨 위와 아래의 층에서는 깊이에 따라 일정한 값을 가지게 되지만, 대류작용이 일어나지 않는 비대류층에서는 깊어질수록 밀도와 함께 다른 온도구배를 이루게 된다. 이러한 솔라폰드의 실험 및 수치적 연구는 여러 연구자들을 통해 수행되었다[2]-[6]. 최근에는 담수화 기술과 연계되어 계절에 따른 열에너지 저장 시스템으로 저렴한 비용으로 구동되는 하이브리드 시스템에 관심이 증대되고 있다.
본 연구는 솔라 폰드 내의 온도를 상승시키기 위해 단열층을 가지는 모델과 그렇지 않은 모델에 대해 기초적인 수치해석을 실시하여 솔라 폰드를 이용한 담수화 및 에너지 저장시스템의 기초 특성을 파악하고자 한다.
2. 계산 모델
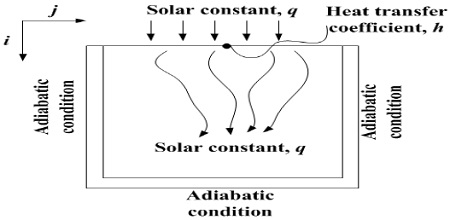
Figure 2은 본 계산의 경계조건을 나타낸 것이다. 계산은 2차원 비정상상태의 조건이고, 솔라폰드의 단열조건과 단열조건이 아닌 경우의 온도의 분포에 대해 추측해 보았다.
수치해석은 유한차분법을 이용하여 각 위치 및 영역에서 사용된 이산화방정식은 Table 1에 나타낸 바와 같다.
본 수치해석의 계산 조건은,
- ① 폰드 내 물의 초기온도는 28℃로 한다.
- ② 토양의 초기온도는 10℃로 한다.
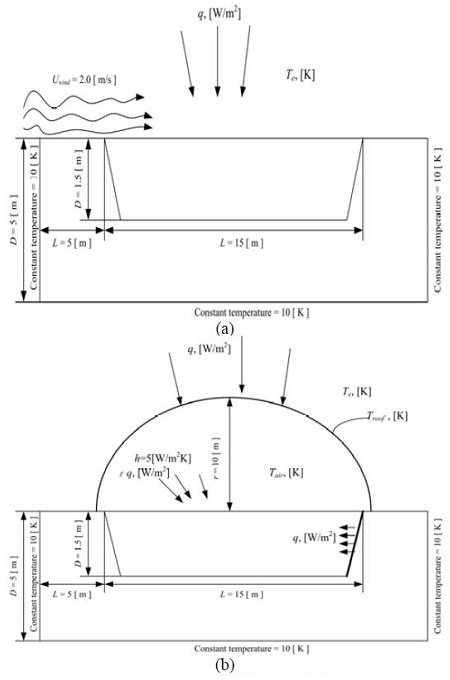
- ③ 계산에서 사용된 스펙은 Figure 3와 같다.
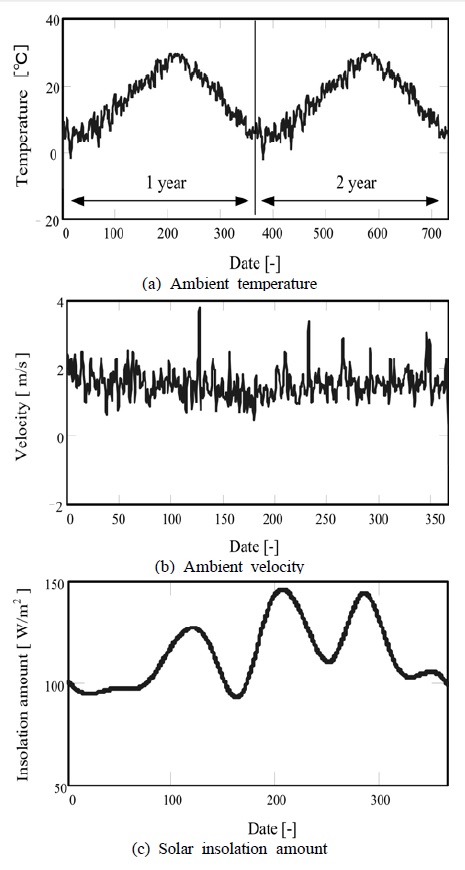
- ④ 계산에서 사용된 파라메터는 대기온도, 태양으로부터의 열량, 풍속이다.
각 각의 파라메터에 대해서는 주로 군산지역의 데이터를 사용했다. 특히, 연간의 기상량 데이터로부터 풍속은 거의 일정하게 2m/s로 사용했다.
기본 방정식은
| (1) |
여기서, ρ는 폰드 내의 물의 밀도[kg/m3], Cp는 폰드 내의 물의 비열[kJ/(kg·K)], k는 폰드 내의 물의 열전도율[W/(m·K)], A는 폰드 내의 표면적[m2], q는 태양으로부터의 열유속[W/m2], x는 임의 위치[m], Ks는 토양의 열전도율[W/(m·K)], Te는 대기의 온도[K]이다.
솔라폰드에 단열조건이 아닌 경우의 대류열전달계수의 계산은
| (2) |
여기서, L는 폰드의 길이[m], Uwind는 풍속[m/s], νwind는 공기의 점도[m2/s]이다.
솔라폰드에 단열조건인 경우의 에너지 방정식은
| (3) |
여기서, qcond는 전도에 의한 열유속량[W/m2], qconv는 대류에 의한 열유속량[W/m2], qrad는 복사에 의한 열유속량[W/m2]이다.
이 때, 솔라폰드의 단열을 위해 설치한 비닐 막에서의 온도 Troof[K]는 식 (4)를 통해서 구한다.
| (4) |
여기서, ε는 복사의 방사율로써 0.85[-], σ는 Stefan-Boltzmann상수 5.67×10-8[W/m2K4], α는 흡수율 0.25[-]이다.
솔라폰드의 단열을 위해 설치한 비닐 내에서의 온도 Tair[K]는 식 (5)를 통해서 구한다.
| (5) |
여기서, h는 대류열전달계수 5[W/m2K]이다.
본 연구에서 수치해석은 공학 계산 툴인 MathCad를 이용하여 수행하였고, 계산의 수렴조건은 10-5으로 하였다.
3. 계산 결과
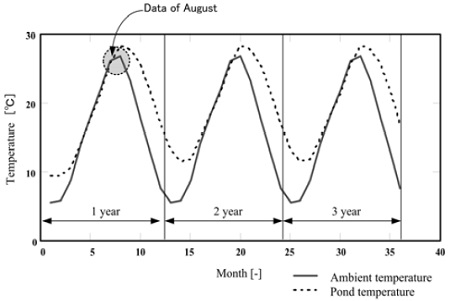
Figure 4은 군산지역의 월별 기상데이터를 사용해 계산을 행한 결과이다. 솔라 폰드 내의 온도가 최대로 되는 8월의 데이터를 초기조건으로써 Figure 5에서 군산지역의 기상데이터로[7]부터 일별 계산을 수행했다.
계산의 시간간격이 길기 때문에 자세한 솔라 폰드 내의 온도라고는 말할 수는 없지만, 계산 결과로부터 알 수 있는 바와 같이 솔라폰드의 계산에 있어서 초기온도 조건으로써 이용하는 것은 충분히 가능하다고 판단된다.
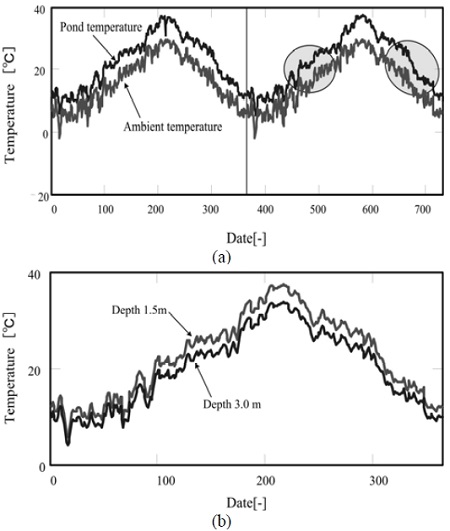
Figure 6 (a)는 15m × 15m × 1.5m의 솔라 폰드 내 물의 온도를 계산한 결과이다. 대기온도의 변화와 함께 정성적으로 유사한 온도변화를 나타내고 있지만, 그 변동폭이 작아지는 것을 확인할 수 있다(Figure 6 (a) ○부분 참조).
Figure 4의 기상데이터로부터 1월부터 3월까지의 일사량이 매우 작기 때문에 1월 15일에 솔라 폰드 내의 온도가 5.8℃까지 내려가는 등 1월부터 3월까지의 솔라 폰드 내의 물의 평균온도는 약 12.5℃정도로 확인된다.
이러한 결과로부터 겨울철의 솔라 폰드 내 물의 온도를 상승시키기 위해서는 폰드의 열용량을 2배로 폰드의 깊이를 3m로 증가시킬 필요가 있다고 판단하여 그 결과를 Figure 6 (b)에 나타냈다. 그러나 폰드의 깊이를 2배(3m)로 증가 시키는 것으로 인해 연중 폰드 내 물의 온도변동은작아지지만, 절대치의 온도는 내려가는 것을 확인하였다. 이 현상은 솔라 폰드의 깊이가 깊어지는 것에 따라 폰드의 하부까지 도달하는 일사량이 줄어들기 때문에 그러한 현상이 일어난 것으로 판단된다.
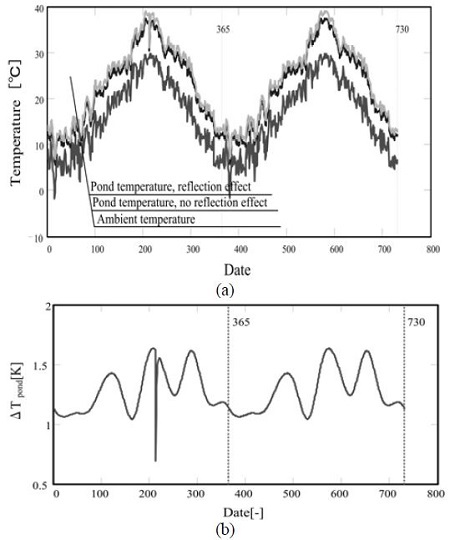
Figure 7 (a)는 솔라 폰드에 일사량을 증가시키기 위한 방법으로써 반사경을 서북방향으로 설치하는 효과로부터 일사량을 2할 증가시켜 계산을 수행한 결과를 나타낸 것이다. 일사량의 증가와 함께 폰드 내 물의 온도가 증가되는 계산 결과를 얻었다.
이 결과로부터 반사경을 폰드에 설치하여 일사량을 증가에 따른 폰드 내의 온도차를 나타낸 것이 Figure 7 (b)이다. 온도의 증가는 1년중 1~1.5℃정도 증가되는 결과를 확인할 수 있었고, x축의 200일 부근에서의 급격한 온도의 변화는 계산의 시작점이 8월 1일이기 때문이다.
그리고, 반사경을 설치하지 않는 경우의 1월 15일에서의 온도가 5.8℃였지만(Figure 6 (a)참고), 반사경을 설치하는 것으로 인한 영향(일사량 2할 증가)으로 인해 1월 15일에서의 온도가 6.9℃로 상승한 것을 확인할 수 있었다.
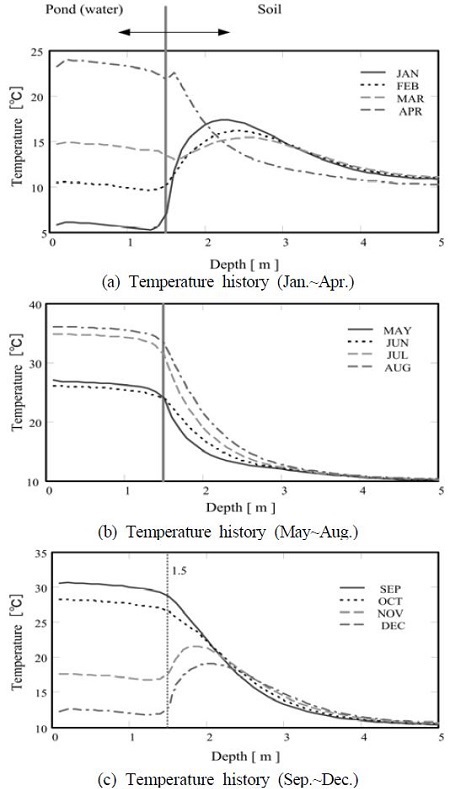
Figure 8 (a), (b)는 상반기(1월~8월)의 솔라 폰드 내 중심온도의 변화를 나타낸 것으로 동기(1월~3월)에서는 토양의 온도가 높은 것을 알 수 있다. 즉, 동기에는 토양으로부터 열이 폰드 내로 전달되는 것을 알 수 있다. 그리고 그 현상은 4월부터는 일어나지 않는 것을 계산 결과로부터 파악할 수 있다. Figure 8 (c)는 하반기(9월~12월)의 온도변화로써 11월부터 다시 토양으로부터 폰드로 열이 전달되는 것을 알 수 있다.
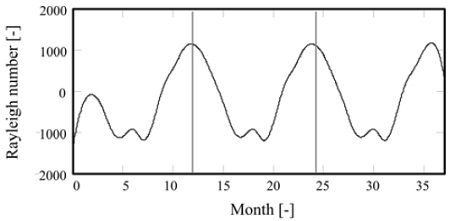
Figure 9은 솔라 폰드 수면으로부터 대기로의 열손실이나 열이동을 방지하기 위해 두께 0.03m의 투명 비닐의 공기층을 설치한 경우에 단열층 내에서의 자연대류의 세기를 나타낸 것이다. 자연대류의 세기를 알아보기 위해 식 (6)으로 Ra 수를 산정하였다.
| (6) |
여기서, β는 체적팽창계수[1/K], g는 중력가속도[m/s2], Tas는 비닐 막 표면온도[K], Tws는 솔라 폰드 수면에서의 온도[K], νa는 공기의 점도[m2/s], ta는 비닐 막 표면에서 수면까지의 길이[m]이다.
Ra = 1708보다 작기 때문에 공기층 내에서의 자연대류에 의한 열의 이동은 없는 것으로 판단된다.
그리고, 동절기에서의 Ra수가 큰 값을 나타내고 있는 것을 확인할 수 있다. 즉, 동절기에는 대기온도가 낮기 때문에 폰드 수면에 접하고 있는 공기층의 온도보다 대기측에 접하고 있는 공기층의 온도가 낮게 되기 때문에 자연대류는 동절기에 강하게 발생하는 것을 알 수 있다.
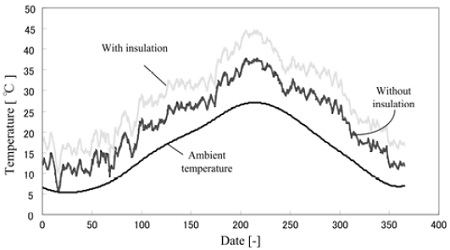
Figure 10는 솔라폰드를 모델로 솔라 폰드 윗면에 공기층으로 인해 단열을 실시한 경우와 하지 않은 경우의 계산결과를 나타낸 것이다. 먼저, 단열을 실시한 솔라폰드의 계산결과로부터 알 수 있는 바와 같이 폰드 내의 온도가약 5[K]이 상승하는 것을 알 수 있다. 즉, 비닐 재질의 막을 설치하는 것으로 인해 폰드 상부공기의 온도가 상승하는 것과 반사판에 의해 일사량을 집중시켜 것 등에 의해 폰드 내의 온도가 큰 폭으로 상승하는 것을 알 수 있었다. 반사판에 의한 영향은 전 일사량의 2배 정도로 가정하여 계산하였다.
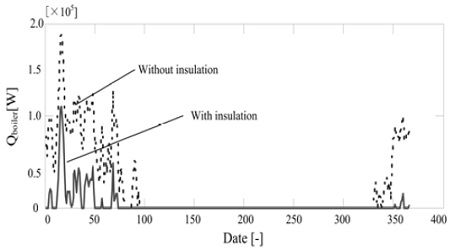
Figure 11은 솔라폰드를 모델로 솔라 폰드 윗면에 공기층으로 인해 단열을 실시한 경우에 계산된 폰드의 온도가 17℃이하로 된 날에는 그 온도를 17℃까지 올리기 위해 요구되는 일당 보일러의 열량을 계산한 결과이다. 결과로부터 알 수 있는 바와 같이 0~60일까지 열량이 집중되고 있다. 당연한 결과이지만, 단열을 하지 않은 경우가 보다 많은 열량이 요구되는 것을 알 수 있다.
태양의 의존율, ηs과 보일러의 의존율, ηb을 식 (7), (8)을 이용하여 각 각 산출해 본 결과 태양의 의존율이 83.3%, 보일러의 의존율이 16.7%로 단열층을 가지는 솔라 폰드의 경우 자연에너지의 의존도가 높은 것을 확인할 수 있었다.
| (7) |
| (8) |
여기서, Qs,sp는 태양에서 단열층을 가지는 솔라폰드로의 입열량 [J], Qb,sp는 단열층을 가지는 솔라폰드 내 물의 온도를 17℃로 유지하기 위해 필요로 하는 보일러의 열량 [J], Qb,p는 단열층을 가지지 않는 솔라폰드 내 물의 온도를17℃로 유지하기 위해 필요로 하는 보일러의 열량 [J]이다.
4. 결 론
본 연구는 솔라폰드의 효율을 향상시키기 위해 구조적으로 단열층을 가지는 경우와 그렇지 않은 경우에 대해 기본적인 수치해석을 실시하여 다음과 같은 결과를 도출하였다.
- 1.겨울철의 솔라 폰드 내 물의 온도를 상승시키기 위해 폰드의 깊이를 1.5m에서 3m로 증가시킨 결과, 솔라 폰드의 깊이가 깊어지는 것에 따라 폰드의 하부까지 도달하는 일사량이 줄어들기 때문에 온도 상승 효과는 발생하지 않는 것을 확인했다.
- 2.솔라 폰드 내에 일사량을 증가시키기 위해 반사경을 서북방향으로 설치한 것을 가정으로 계산을 수행한 결과, 동절기에 온도 상승 효과를 확인할 수 있었다.
- 3.동절기에는 토양의 온도가 솔라 폰드 내 물의 온도보다 상대적으로 높아 토양에서 폰드 내로 열이 전달되는 것을 확인할 수 있었다.
- 4.단열층을 가지는 솔라폰드의 경우 단열층 내의 자연대류의 세기를 산출해 본 결과, Ra=1708보다 작기 때문에 공기층 내에서 자연대류에 의한 열의 이동은 없는 것을 판단되었다.
- 5.단열층을 가지는 솔라폰드의 경우, 태양의 의존율은 83.3%, 보일러의 의존율은 16.7%로 자연에너지의 의존도가 높은 것을 확인할 수 있었다.
References
- H. Y. Park, K. B. Lim, “A study on the behaviors of several layers in a solar pond”, The Korean Society of Mechanical Engineers, 11(2), p304-313, (1987), (in Korean).
-
H. Stommel, B. Arons, and D. Blanchard, “An oceanographical curiosity: The perpetual salt fountain”, Deep Sea Resource, 3(2), p152-153, (1953).
[https://doi.org/10.1016/0146-6313(56)90095-8]

- A. V. Kalecsinsky, Ueber die ungarishen warmen und heissen kochsalzseen als natuerlich waemeaccumulatoren, Ann. Physik Ⅵ, p408, (1902), (in German).
-
H. Weinberger, “The physics of the solar pond”, Solar Energy, 8(2), p45, (1964).
[https://doi.org/10.1016/0038-092X(64)90046-5]

-
J. S. Turner, “Double-diffusive phenomena”, Ann. Rev. Fluid Mech, 6, p37-56, (1974).
[https://doi.org/10.1146/annurev.fl.06.010174.000345]

-
H. Tabor, “Solar ponds”, Solar Energy, 27(3), p181-194, (1981).
[https://doi.org/10.1016/0038-092X(81)90120-1]

- http://www.kma.go.kr Accessed July 1,2014.