베어링 강성을 고려한 10,100 TEU 컨테이너 운반선의 최적 추진축계 배치에 관한 사례 연구
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
선박이 고출력화, 초대형화 됨에 따라 대형저속 2행정 엔진을 탑재한 선박에서 축계배치의 잘못에 기인하는 주기관 선미측 베어링과, 선미관 후부 베어링의 손상이 증가하는 경향이 있다. 또한 고출력화에 의한 추진축의 강성은 증가한 반면에 선체는 고장력 후판을 사용하므로 이전의 선체보다 훨씬 더 쉽게 변형하는 실정이다. 이는 기존의 선박보다 더욱 정교한 축계배치가 요구됨을 의미한다. 본 연구에서는 열팽창 효과, 감도지수를 이용한 중간축 베어링의 최적위치 선정 및 베어링의 강성을 고려하여, 베어링의 하중 분석 및 영향 계수를 분석함으로서 축계 배치가 이론적으로 최적이 되는 것을 검토하였다. 이를 위하여 축계 배치 계산시 대형 엔진 제조사의 엔진 거치기준을 참조하고, 한국선급 및 DnV 선급의 축계 배치 프로그램을 이용하여 검토하고 그 신뢰성을 검증하였다.
Abstract
Damages of the main engine aftmost bearing and the after stern tube bearing tend to increase due to misalignment. And as the shafting system becomes stiffer due to the large engine power, whereas the hull structure becomes more flexible due to optimization by using high tensile thin steel plates. And this is the reason that more sophisticated shaft alignments are required. In this study, the optimum shafting alignment calculation was carried out, considering the thermal expansion effect, exploiting the sensitivity index, which indicates the reasonable position of forward intermediate shaft bearing for shaft alignment. and as the main subject in this study, the elastic deformation on intermediate shaft and main engine bearings occurred by vertical load of shaft mass were examined thoroughly and analyzed allowable load of bearings, reaction influence numbers of all bearings. As the result, a reliable optimum shafting alignment was derived theoretically. To verify these results, they were referred to the engine maker's technical information of main engine installation and being used shafting alignment programs of both Korean Register of Shipping and Det Norske Veritas, their reliability were reviewed.
Keywords:
Shaft alignment, Sensitivity index, Bearing stiffness, Reaction influence number키워드:
축계 배치 계산, 감도지수, 베어링 강성, 반력영향계수1. 서 론
선박의 추진축계를 잘못 배치할 경우 각 베어링의 하중 배분이 고르지 못하게 되므로 결과적으로 베어링의 이상마모, 과부하, 무부하 상태, 또는 과열, 감속기어의 마모, 파손 등의 문제가 발생할 수 있다. 추진축계 배치에 관한 연구는 1950년대 후반 미국 해군 함정에서 중요성이 대두된 이후 1960년대 후반부터 1970년대 초반에 걸쳐 개개의 베어링에 대한 최적의 위치를 결정하는 주요 이론이 정립되었다[1]-[4]. 최근 선박이 고출력화, 초대형화 됨에 따라 추진축의 강성은 증가한 반면에 선체는 철강기술의 발전으로 인하여 더 얇은 고장력 후판을 사용하므로 선체의 후미부는 이전의 선체보다 훨씬 더 쉽게 변형되는 실정이다. 이는 기존의 선박보다 더욱 정교한 축계배치가 요구됨을 의미한다. 따라서 추진축계 배치의 최적치를 설계 단계에서 얻기 위해서는 해석 시 선박의 적하 하중에 따른 베어링 반력의 변화, 운항에 따른 메인 엔진의 변형 및 프로펠러 추력에 의해 발생되는 굽힘모멘트, 하중에 대해 연직방향으로 작용하는 베어링의 탄성변형 등을 함께 고려하여야 한다[5][6]. 본 연구에서는 10,100 TEU급 컨테이너 운반선에 대하여 이러한 사항을을 고려한 축계 배치분석을 수행하여 축계 배치가 이론적으로 최적이 되는 방안을 모색하였다. 이를 위하여 대형 엔진 제조사의 엔진 거치기준을 참조하고, 한국선급 및 DnV 선급의 축계 배치 프로그램을 이용하여 검토하고 그 신뢰성을 검증하였다.
2. 추진축계 배치문제 및 설계개요
2.1 축계배치와 베어링 영향계수
축계배치에 있어서 축계의 유연성을 나타내는 척도로 베어링 영향계수 (influence number)를 사용하는데, 이는 각 베어링의 지지점 위치가 동일 수평면 상에 있고 그 중 한 개의 지지점만을 단위높이(통상 1mm)만큼 상승 또는 하강시켰을 때 나타나는 다른 베어링의 반력 변화량을 말한다. 이는 주로 축의 강성 및 베어링 간의 거리에 의해서 결정되는데, 베어링 영향계수가 작을수록 선체변형에 더 유연하다고 할 수 있다[7].
2.2 축계 배치상 문제점
선박에 있어서의 추진축계는 디젤 주기관을 갖는 경우 크랭크축, 추력축, 중간축, 프로펠러축으로 구성되며 경우에 따라서는 감속 기어장치를 설치하게 된다. 이들 중 축계배치문제와 가장 밀접한 관계를 갖는 것은 감속기어장치, 추력축을 포함하는 중간축, 프로펠러를 포함하는 프로펠러 축 등이다. 이들이 축계배치와 관련하여 문제되는 것은 다음과 같다.
감속 기어장치 설치시, 기어 축 양단의 베어링 설치 옵셋이 부적절 할 경우 기어간 접촉 불균일로 인한 접촉면의 마모, 소음, 진동 및 손상을 일으킬 수 있다. 따라서 기어 제작자에서 제공하는 기어의 운전상태시 축 베어링이 축의 하중을 적절히 분담하기 위해 제공하는 허용치를 참고하여야 한다.
중간축 설치시 유의점은 중간축 베어링의 종방향 위치와 수직방향 위치(옵셋)에 관한 것들이 있다. 중간축 베어링과 인접한 베어링간의 거리가 짧을수록 해당 중간축의 영향계수가 커지게 되므로[8] 인접 베어링에 불필요한 부하를 가지게 하며, 반면에 인접 베어링간의 거리가 길수록 축계의 유연성은 증가하나 횡진동을 야기할 수 있다[9].
또한 옵셋이 적절하지 않아 베어링이 축을 지지하지 않는 무부하 상태가 될 경우 횡진동에 취약해 질 수 있으며, 반대로 과부하 상태가 될 경우 유막 손상에 기인한 베어링의 스크레치(scratch), 와이핑(wiping) 같은 열손상(thermal damage)이 발생할 수 있다.
2.3 추진축계 배치시 고려사항
따라서 축계배치시 다음과 같은 사항을 고려하여야 할 것이다.
- (1) 드라이 독 상태, 진수상태 등의 흘수 변경에 따른 엔진 프리색(pre-sag) 등 경험적인 선체의 변형량
- (2) 냉간상태(cold Condtion), 온간상태(hot conditon)간의 온도차로 인한 축계 베어링의 열팽창
- (3) 동적상태(dynamic Condition) 시 발생하는 프로펠러 편심 추력
- (4) 베어링 마멸(특히 해수윤활 lignum vitae의 경우)
- (5) 축이나 프로펠러의 회전에 의한 불평형 관성력
- (6) 가능한 한 선미관 후부 베어링에서 하중의 분포가 균일할 것, 즉 선미단에 베어링 하중이 국부적으로 편중되지 않을 것
감속기어를 갖는 터빈이나 디젤기관에서는 감속 기어장치가 비교적 짧기 때문에 축계 중심선의 평균 기울기가 베어링 중심선에 평행하게 되도록 축계 지지대나 베어링 및 감속 기어장치를 여기에 맞도록 낮추어서 배치할 수 있다. 그러나 저속 디젤기관은 상응하는 기울기를 갖도록 설치하기에는 너무 길기 때문에 선미관 베어링에 상응하는 기울기를 갖도록 보링(boring)하거나 베어링 부시(bush)의 외경을 상응하는 기울기가 되도록 가공한다. 후자의 방법이 정확한 기계가공이 가능하기 때문에 바람직한 방법이다. 또한 선미관 백색 합금(white metal) 베어링에서 모서리에 하중이 국부적으로 편중되는 현상을 완화하기 위하여 후부 베어링 길이 1/3 정도를 경사지게 보링 가공하기도 한다.(부분경사 보링 또는 이중경사 보링)
2.4 추진축계 배치계산의 기준
기름 윤활을 할 때 대부분의 선급(KR, DnVGL, LR, ABS, BV, NK)에서 제시하는 선미관 베어링의 최대 허용 면압은 0.8 N/mm2 미만을 만족하여야 하며, 또한 베어링 각각에 대해서는 베어링 제작업체의 추천값을 참고하는 것이 일반적이다.
▪ 기름 윤활식 선미관 베어링 : max. 0.8 N/mm2
▪ 해수 윤활식 합성수지 베어링 : max. 0.6 N/mm2
▪ 중간축 베어링 : max. 1.2 N/mm2
허용면압은 베어링에 작용하는 하중을 베어링 길이에 대한 투영면적으로 나눈 값을 의미한다.
문헌[9]에 의한 허용치는 통상
▪ 프로펠러 축 : 15～25 N/mm2
▪ 중간축 : 10～25 N/mm2
▪ 추력축 : 20 N/mm2
이며, 축의 재질에 따라 허용 굽힘 응력이 결정되지만, 축계의 굽힘 응력을 과도하게 제한하는 것은 축계배치에 있어서 바람직하지 않을 수도 있다. 유연한 축계 배치 일수록 큰 굽힘응력이 발생하므로 횡진동(whirling vibration) 및 피로강도를 만족하는 범위 내에서 어느 정도의 높은 굽힘응력 상태는 성공적인 축계 배치의 반증으로 볼 수 있다.
선미관 부후 베어링에서 국부하중으로 인한 베어링 손상을 최소화 하기 위하여 대부분의 선급에서는 프로펠러 축과 선미관 후부 베어링 사이의 상대 경사각이 0.3mrad을 초과하지 않아야 한다고 명시하고 있다.
3. 실선 축계의 최적배치 방안 연구
이 장에서는 추진축계 배치 시 고려하고 있는 대표적인 방법들을 이용하여 계산을 수행하고 그 결과를 검토하였다. Table 1은 본 연구에 이용한 실선의 축계 주요 사양이다.
Specifications of shafting system
3.1 감도지수를 이용한 중간축 베어링 위치 최적화 검토
선박흘수 변화에 따라 베어링 옵셋이 변경될 때, 축 방향에 있어서 중간축 베어링의 설치위치는 최후단부 엔진 베어링의 반력에 큰 영향을 미친다. 실제로 중간베어링이 최후단부 엔진 베어링에 매우 근접하게 설치되어, 운항을 시작한지 얼마 되지 않은 선박이 엔진 후부 베어링에 열손상을 입은 사례도 있다. 중간축 베어링을 축방향으로 배치할 때, 베어링의 위치를 이론적인 접근보다는 경험에 의존하여 결정하여 왔다. 일반적으로 베어링 위치를 선정할 때 엔진 최후단부에 미치는 영향을 줄이기 위하여 중간베어링을 엔진으로부터 최대한 멀리 설치하는 것이 효과적이다. 반면, 위와 같은 접근법으로 중간축 베어링이 지나치게 선미관 베어링에 근접하게 되는 경우 해당 중간축 베어링의 영향 계수가 커지게 되므로, 설계자는 양 측의 균형을 유지할 수 있는 판단력이 필요하다. 일반적으로 중형화학제품 운반선과 같이 단축을 가진 선종의 경우 감도지수에 매우 민감한 것으로 조사되었다[10].
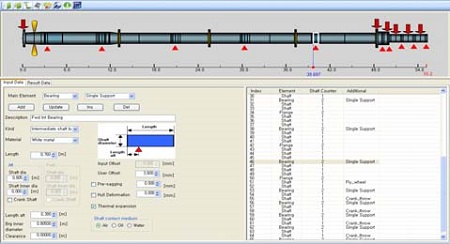
본 논문의 대상인 선박의 축계는 길이가 70미터에 달하고, 중간축이 Aft-Mid-Fwd 3개로 이루어진 초장축이다. 본 논문에서는 베어링의 감도지수를 이용한 계산의 목적이 엔진측에 지나치게 가깝지 않은 위치에서 가장 유연한 축계를 만드는 것에 있으므로 Fwd(전부) 중간축을 대상으로 베어링 감도지수법을 이용하여 베어링의 최적위치를 산출하였다. 이를 위한 계산도구로 Figure 2와 같이 한국선급의 추진축계 배치 프로그램을 이용하였다.
Shaft alignment program
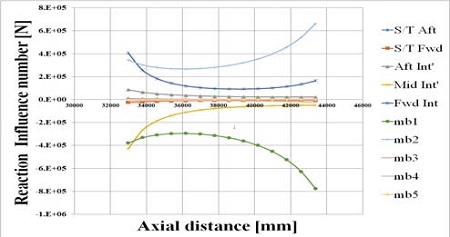
Figure 3은 Fwd(전부) 중간축 베어링 위치를 중간축 선미 끝단에서부터 선수 끝단까지 일정간격으로 움직일 경우 해당 위치에서 중간축 베어링이 각 베어링의 영향계수에 미치는 영향을 나타낸 것이다.
Reaction influence number (N)
Figure 3에서 중간축 베어링(Fwd Inter.) 자체의 영향 계수로 판단해 볼 때, 중간축 베어링의 위치가 프로펠러 축단으로부터 39,388mm일 때 가장 낮은 민감도를 가졌다. 그러나 첫 번째(mb1), 두 번째 엔진 후부 베어링(mb2)에 미칠 영향을 고려한다면, 중간축 베어링은 보다 선미측인 36,188mm로 배치되는 것이 보다 적절한 것으로 판단된다.
상기의 결과는 민감도가 최소가 되는 관점에 있어서 중간축의 최적베어링위치를 제안한 것이므로 중간축 베어링 위치가 다른 베어링에 미치는 영향을 고려하기 위한 감도 지수(sensitivity index)산출은 아래 식 (1)과 같이 표현될 수 있다[8].
| (1) |
여기서 N은 감도지수 산출시 고려된 베어링의 총 개수, m은 중간축 베어링 번호이고, Rmi는 선미관 선미측 베어링으로부터 기산하여 i번째 베어링에 대한 중간축 베어링의 영향계수를 의미한다.
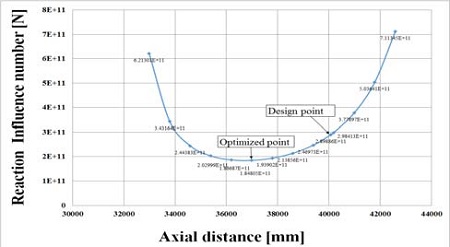
식 (1)을 적용한 결과를 Figure 4와 같이 나타내었다. 그림과 같이 선미관 전부 베어링이 있는 축계에서 민감도가 최소화 되는 중간축 베어링의 위치는 36,988mm인 것으로 나타났다. 감도지수만을 고려할 때 중간축 베어링은 36,988mm 위치에 설치하는 것이 바람직하지만 실선 적용 시에는 엔진룸 내 선체 이중저 구조부재의 간섭과 탱크위치를 고려하여 실선에는 최종 40,077mm위치에 배치하였다.
Sensitivity index from aft end flange to bearing center at Fwd intermediate shaft [mm]
따라서 상기와 같이 배치한 중간축의 위치가 10,100 TEU Container 선박의 최적의 Fwd(전부) 중간축 베어링의 최적 위치임을 감도 지수를 이용하여 확인할 수가 있었다.
3.2 축계 강체 베어링 반력 해석
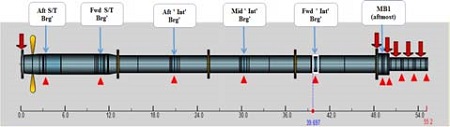
선박의 적재상태에 따른 흘수의 변화, 해상상태 등 선체의 변형에 영향을 미치는 모든 조건을 고려하여 추진축계의 베어링 반력을 해석하는 것은 현실적으로 어려운 상황이다. 다만, 축계의 정적, 동적상태에서 엔진의 온도, 베어링 탄성변형에 따른 축계 배치에 관하여는 해석이 가능하다. 아래의 Figure 5, Figure 6 은 프로그램에 사용된 모델 및 10,100 TEU 선박의 축계배치도이다.
Shaft modeling for analysis
Drawing of shafting system
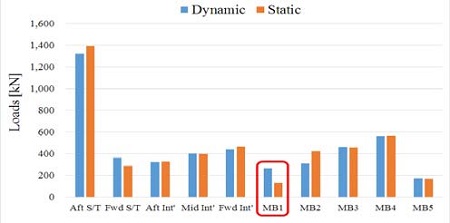
이를 검토하여 보면 Figure 7와 같이 선박이 냉간정지 상태에서와 운전상태에서 발생하는 엔진 최후단부 베어링(MB1)의 하중이 가장 민감하게 변동하는 것을 확인할 수 있다. 이는 메인 엔진의 열팽창 효과 및 베어링의 탄성변형으로 인한 옵셋 변화에 의해 기인한다.
Deviation of reaction forces between dynamic and static alignment conditions
3.3 베어링 강성을 고려한 베어링 반력 분석
엔진 베어링에 가해지는 하중에 따른 베어링 지지점의 연직방향 베어링 강성을 선형적으로 고려한 탄성변화를 계산하고 이를 통하여 최적 축계배치의 신뢰성을 검증하기로 한다.
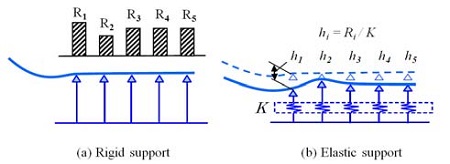
Figure 8은 축 자중 및 프로펠러 중량에 따른 베어링 지지점의 연직방향 베어링 강성을 선형적으로 고려한 탄성 변형이 일어나기 전 상태에서 엔진베어링 지지점의 강성을 어떻게 다루어야 하는지를 보여준다. 축계 배치 계산에서 강체지지를 고려하는 경우, Figure 8 (a)에서처럼 하중으로 인한 처짐이 발생하지 않기 때문에 주어진 옵셋에 대응하는 베어링 각각의 반력 Ri을 쉽게 얻을 수 있다. 반면에, 강성이 고려될 경우, 지점은 Figure 8 (b)에서처럼 하중에 의해 실제로 연직방향 하부로 이동한다. 그리고 이것은 실제로 베어링 각각의 반력Ri의 변화를 발생시킨다.
Deviation between Rigid and elastic support for main engine bearings
탄성이 고려되는 경우라도 반력Ri는 변하지 않는다고 가정하면, 하중이 주어지는 경우의 각 베어링 지지점의 변위hi는 다음 식 (2)와 같이 각 지지점의 스프링상수 K 값을 이용하여 구할 수 있다.
| (2) |
본 논문에서는 선체 변형을 고려하지 않고 엔진 베어링에 가해지는 하중에 따른 베어링 지지점의 연직방향 베어링 강성을 식 (2)을 이용하여 선형적인 탄성변화를 고려하였다. 또한 탄성베어링으로 간주하는 부분은 대부분의 대형조선소에서 계산하는 방법과 같이 주기관 베어링만을 탄성베어링으로 간주하였다. 탄성지지 되는 베어링의 최종 옵셋은 하중으로 인한 베어링 강하량과 틈새로 인한 축의 강하량의 합으로 결정된다. (참고로 베어링과 축의 틈새가 x[mm]이면 틈새로 인한 축의 강하량은 0.5 x[mm]가 된다.) 본 논문에서는 축계 전 베어링의 틈새 기 반영된 것으로 간주하였다. 또한 주기관 베어링의 스프링상수 K는 엔진 제조사의 기술자료를 통하여 확인한 5,000kN/mmm 값을 이용하였다. 상기에 따른 축계 배치 검토를 위하여 한국선급의 축계배치 프로그램[11]을 사용하였고 계산 결과의 정밀도를 확인하기 위하여 DnV 선급의 축계 배치 프로그램 결과와 비교함으로서 그 신뢰성을 확인하였다. Table 2 는 한국 선급의 축계 배치 프로그램을 이용하여 계산한 탄성베어링의 옵셋결과이고, Table 3는 DnV 선급의 축계 배치 프로그램을 이용하여 계산한 탄성베어링의 옵셋결과이다. 양 선급 프로그램의 결과는 매우 유사함을 확인하였다.
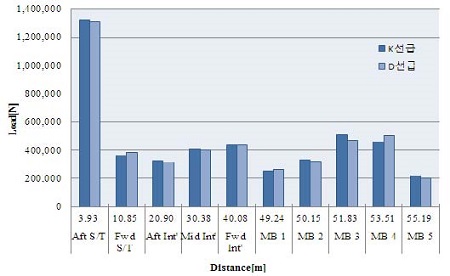
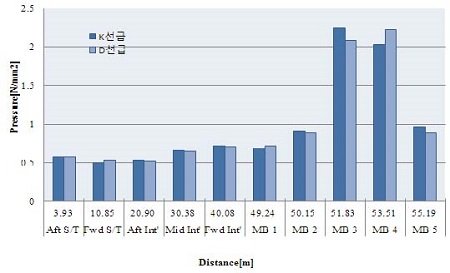
Figure 9, Figure 10은 산출된 베어링 옵셋을 적용하여 양 프로그램간 베어링 반력 및 면압을 비교한 것이다.
계산결과를 고찰하였을 때 각 베어링 반력과 면압의 경향이 같고, 계산값의 편차는 매우 근소하였으며 계산결과는 모두 2.4 항의 추진축계 배치 기준치를 만족함을 확인하였다.
Calculation result using KR program
Calculation result of using DnV program
Comparison of bearing load between KR and DnV
Comparison of bearing pressure between KR and DnV
4. 결 론
본 연구의 결과를 요약하면 다음과 같다.
- (1) 장축을 가지는 10,100TEU 컨테이너선 축계의 최적 배치를 위하여 선박의 정지/운전 상태에서 축계배치를 수행하고, 더 나아가 주기관 베어링 개수, 열팽창 효과를 고려하여 축계 배치계산을 수행하였으며. 베어링의 하중 분석 및 영향 계수를 분석하여 축계 배치가 이론적으로 최적이 되는 방안을 모색하였다.
- (2) 또한, 반력영향계수를 이용한 감도지수(sensitivity index)를 사용하여 이 값이 가장 작게 되는, 즉 베어링의 상태변화에 대하여 가장 민감도가 낮은 위치를 분석함으로써 최적의 베어링 위치를 결정하는 방법을 소개하였다. 다만 이 경우에 선미 구조상 베어링을 원하는 위치에 설치하기에 어려움이 있어 가능한 범위에서 그 위치에 가깝도록 하였다.
- (3) 연직방향 엔진베어링 강성을 선형적으로 고려하여 이에 따른 결과와, 강체 지지로 했을 경우의 결과를 비교하여, 축의 거동에 따른 다양한 계산을 통하여 만족스러운 결과를 얻었다. 이러한 방법은 본 사례 뿐만 아니라 긴 추진축계를 갖는 유사 선박에도 적용할 수 있을 것으로 사료된다.
- (4) 두 선급에서 독자적으로 개발하여 사용 중인 축계배치 프로그램에 의한 계산 결과의 차이가 미미함을 보여주었다. 따라서 어느 선급의 프로그램이나 결과의 정밀도에 있어서는 차이가 없기 때문에 축계 배치 프로그램의 선택은 사용상의 편리함에 따라 결정할 필요가 있을 것으로 사료된다.
References
-
R. Michel, “A quarter century of propulsion shafting design practice and operating experience in the U.S. Navy,”, Naval Engineers Journal, p153, (1959).
[https://doi.org/10.1111/j.1559-3584.1959.tb05306.x]
- H. C. Anderson, and J. J. Zrodowski, “Co-ordinated alignment of line shaft, propulsion gear, and turbines,”, Society of Naval Architects and Marine Engineers, 67, p449-523, (1959).
- W. E. Lehr, “Considerations in the design of marine propulsion shaft system,”, Society of Naval Architects and Marine Engineers, 67, p555, (1961).
-
G. Mann, “Shipyard alignment of propulsion shafting using fair curve alignment theory,”, Naval Engineers Journal, 77(4), p651-659, (1965).
[https://doi.org/10.1111/j.1559-3584.1965.tb04996.x]
- Y. J. Lee, A Study on Hull Deflections Effecting the Ship’s Propulsion Shafting Alignment, Ph.D. Dissertation, Department of Mechanical Engineering Graduate School, Korea Maritime University, Korea, (2006), (in Korean).
- American Bureau of Shipping, Guidance Notes on Propulsion Shafting Alignment, Houston, USA, American Bureau of Shipping, (2006).
- K. C. Kim, and J. G. Kim, “A study on optimum shaft alignment analysis for VLCC,”, Proceedings of the Special Transactions of the Society of Naval Architects of Korea, p134-137, (2005), (in Korean).
- Class NK, GUIDELINES ON SHAFTING ALIGNMENT, Japan, Class NK, (2006).
- H. J. Jeon, Ship Propulsion Transmission Equipment, Busna, Korea, Taehwa Publishing Company, (1986), (in Korean).
- C. O. Seo, A Study on the Optimal Shafting Alignment for Chemical Tanker of Medium Size, M.S thesis, Department of Marine System Engineering Graduate School, Korea Maritime and Ocean University, Korea, (2010), (in Korean).
- Korean Register of Shipping, SeaTrust-SHALI Shaft Alingment Program User Manual, Korea, (2009), (in Korean).