Subset selection in multiple linear regression: An improved Tabu search

1. Introduction

An important subset selection, which is a vital combinatorial optimization problem in multivariate statistics, is considered in this paper. The objective of the problem is to provide faster and more cost-effective predictors for the purpose of improving the prediction performance [1]. Its applications widely range from machine learning, time-series prediction, and multi-class classification to noise detection.

In this paper, we focus on the variable selection problem of multiple linear regression models. It is the selection of the optimal subset of variables in order to reliably construct a multiple linear regression model. There is no doubt that the allpossible regression approach called exact method is the best because it examines every possible model for the p independent variables. However, since this problem has NP-complete nature, it becomes more difficult to find the optimal solution by allpossible regression approach. When the number of variable generally exceeds 40, it is no longer practical to obtain the optimum by exact methods. Exact methods are based on the branch-and-bound (BNB) algorithm. Furnival and Wilson [2] proposed the earliest BNB algorithm for this problem of multiple linear regression model. Many authors have further developed the efficient BNB algorithms (Duarte Silva [3][4], Gatu and Kontoghiorghes [5], Hofmann et al.[6], Brusco et al. [7], and Pacheco et al.[8]).

Heuristic methods are more frequently used for the large size of the subset selection problem. Heuristic methods are usually classified into two categories: simple heuristics and meta- heuristics. Simple heuristic methods involve forward selection, backward elimination, and stepwise regression. The computing time for simple heuristics is fast, but the solution quality is generally poor. Metaheuristic methods have been developed to provide better solution quality than simple heuristics. Two typical metaheuristic methods have been used previously to solve the optimal subset selection problem: tabu search (TS) [9] and hybrid genetic and simulated annealing algorithm (GSA) [10]. However, these two methods have shortcomings. The tabu search method requires a large amount of computing time, and the hybrid GSA method produces a less accurate solution.

To overcome their shortcomings, we propose an improved tabu search to reduce moves of the neighborhood and to adopt an effective search strategy for neighborhoods. To evaluate the performance of the proposed method, comparative studies are performed on small literature data sets and on large simulation data sets.

The remainder of this paper is organized as follows. The model of subset selection problem is introduced in Section 2. In Section 3, the previous two metaheuristic methods, which are TS [9] and hybrid GSA [10] are briefly described, and we propose an improved tabu search in Section 4. In Section 5, the results of the computational experiments on both benchmark problem [10] and simulation data sets are presented. Finally conclusions are offered in Section 6.

2. The Subset Selection Problem

Finding an appropriate subset of regressor variables for the model is usually called the subset selection (or variable selection) problem. It is the selection of the optimal subset of variables in order to reliably construct a multiple linear regression model.

Let p the number of independent variables in the full model and k the number of independent variables selected in the model. The subset selection model is as follows.

There are 2^p − 1 possible subset models. When p > 40, computational burdens to construct optimal subset model are increased exponentially due to the NP-complete nature of the problem.

For the subset selection problem, several measures with respect to the selection criteria have been proposed such as adjusted R², Mallow’s Cp, and Akaike’s AIC (see Draper and Smith [11] and Mogomery et al.[12]). In this paper, we focus on the selection criterion of adjusted R². The adjusted R² is given by

where SSS_k is residual sum of squares for the k-variable model, SST is total sum of squares, and n is the number of observations.

3. The Previous Metaheuristic Methods

3.1 TS (Drezner [9])

Tabu search, designed to escape from local optimum, is a metaheuristic algorithm for solving optimization problems. Motivated by Glover [13] as an optimization tool applicable to nonlinear covering problems, the TS algorithm was originally proposed by Glover [14]. The basic idea of the TS is to expand its search beyond local optimality using adaptive memory. The adaptive memory is a mechanism based on the tabu list of prohibited moves. Use of the tabu list is one way to prevent cycling and guide the search towards unexplored region of the solution space.

The tabu search algorithm has been successfully applied to telecommunications path assignment [15], neural network pattern recognition [16], machine learning [17], just-in-time scheduling [18], and electronic circuit design [19].

Drezner [9] developed a tabu search for the subset selection problem. The TS procedure is described in the following pseudocode.

Drezner [9] generated all neighborhoods by three moves, which are adding a variable, removing a variable, and swapping variables. For example, consider a set of p = 5 independent variables: full-set = {x₁, x₂, x₃, x₄, x₅} and a subset of k= 2 variables: {x₁, x₂}. All neighborhoods of this subset consist of the following moves in Table 1.

Table 1:

All neighborhoods of subset {x1,x2}

Drezner [9] also adapted the stopping criterion as the total number of 30 iterations without improving the best-so-far solution. The size of the tabu list was set to 10.

3.2 Hybrid GSA

Lin et. al.[20] suggested the original version of GSA for solving some NP-hard problems such as knapsack problem, travelling salesman problem, and set partitioning problem. Hasan [10] proposed a hybrid GSA for the subset selection problem, in which a genetic algorithm (GA) [21] is combined with a simulated annealing (SA) algorithm [22]. The pseudocode for the hybrid GSA algorithm is as follows.

The SA operator is incorporated into the generation of children produced by the genetic operators. It is applied to decide which two of the parents and children remain. That is, if children are better than parents, then the parents is replaced by the children. If parents are better, they are replaced with the chosen probability as shown in the pseudocode of GSA.

Hasan [10] suggested that the number of the population, crossover rate, mutation rate, maximum number of iteration, the initial temperature and the cooling rate is chosen as 100, 0.8, 0.1, 1000, 100 and 0.9, respectively.

4. The Proposed Method

An improved tabu search (ITS) is proposed in this paper for solving the subset selection problem. The proposed method addresses shortcomings in two typical metaheuristic methods that have previously been developed. The tabu search method takes a large amount of computing time, due to many neighborhood moves, and the hybrid GSA method produces a less accurate solution. The proposed method is a fast tabu search that reduces moves of the neighborhood and adopts an effective search strategy for neighborhoods.

4.2 Search Strategies for Neighborhoods

Widmer & Hertz [23] and Tailard [24] proposed tabu search for the flow shop scheduling problem. They also suggested two specific search strategies: the best move strategy and the first move strategy. The best move strategy examines all neighborhoods and selects the best move that is not on the prohibited tabu list. The first move strategy examines the neighborhoods and selects the first move that improves the current best solution. If there is no first move that improves the current best solution, the first move strategy eventually becomes equivalent to the best move strategy.

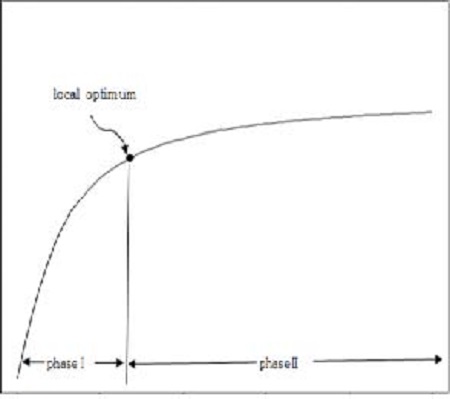
As depicted in Figure 1, the procedure of improving the best solution can be divided into two phases: Phase-I and Phase-II. In the Phase-I, the procedure for improving the best solution is rapidly progressed. After the solution reaches a local optimum through the tabu search, it is difficult to improve the local optimum. Accordingly, the procedure of improving the local optimum is slowly processed in the Phase-II

Figure 1:

The Phase-I and Phase-II

In the improved tabu search, the first move strategy is adopted.

In Phase-I, the first move strategy plays a role in rapidly improving the current best solution.

The pseudocode of the first move strategy is as follows.

5. Computational Results

Comparative analytical tests were performed to compare the proposed method with the two previous metaheuristic methods. Experiments were initially performed using data sets obtained from the literature to evaluate their performance. These data sets consisted of a small number of variables (less than 24). To further evaluate the performance of the proposed method for large number of variables, we randomly generated large data sets up to 100 variables. That is, the number of variable varies from 40, 60, 80 to 100. Results for the small literature data sets are reported in the Section 5.1. Computational results for the large simulation data sets are summarized in the Section 5.2. All computational experiments were conducted on an Intel i7 PC with 3.4 GHz CPU and 8 GB RAM, and all source codes were implemented with R language.

5.1 The Benchmark Problem

In Table 2, p, n, Best, and Freq. are defined as follows.

Table 2:

Experimental results of GSA, TS (Drezner [9]) and ITS (Improved TS)

p : the total number of independent variables.
n : the number of sample data.
Best : the Maximum of $$ R_{\mathit{adj}}^2$$ for 10 trials.
Mean : the Mean of $$ R_{\mathit{adj}}^2$$ for 10 trials.
Freq : the number of Best found by each method for 10 trials.

As the experimental results in Table 2 indicate, all methods find the optimal value of $$ {\mathrm{R}}_{\mathrm{adj}}^2$$. In the value of Freq., however, the performance of TS is more or less worse than that of the proposed ITS method.

5.2 Simulation Data Sets

To further test the performance of the ITS method, the simulation data sets were randomly generated as follows.

i) Independent variables were generated by normal distribution with a mean 0 and a standard deviation 1.

ii) Error terms were generated by normal distribution with a mean 0 and a standard deviation λσ, where σ is standard deviation of actual regression equation, and λ is a constant.

iii) The number of sample data is five times the total number of independent variables.

The value of E is given by the following Equation (3).

$\[ E=\frac{\mathrm{k}}{\mathrm{p}}, \]$

(3)

where k is the number of sample data and is five times the total number of independent variables, and p is the total number of independent variables.

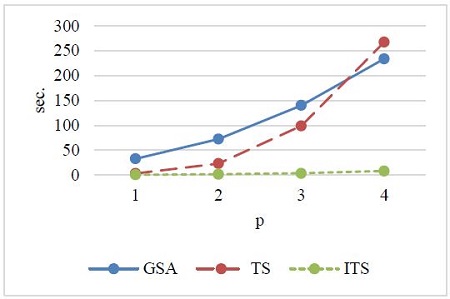
From the computational results shown in Tables 4 to 7, it is clear that the proposed ITS method outperforms the GSA and TS methods in terms of the computing time and solution quality. As shown in Figure 2, the ITS method is the fastest. Specifically, when the value of p is 100, the GSA and TS methods take a considerable amount of computing time. As seen in Table 3, the computing time (sec.) of GSA, TS, and ITS is 233.8, 267.5 and 8.058, respectively.

Figure 2:

The Computing Time of GSA, TS and ITS

Table 3:

The computing (sec.) of GSA , TS and ITS

Table 4:

Experimental results of GSA, TS and ITS (p=40, n=200)

Table 5:

Experimental results of GSA, TS and ITS (p=60, n=300)

Table 6:

Experimental results of GSA, TS and ITS (p=80, n=400)

Table 7:

Experimental results of GSA, TS and ITS (p=100, n=500)

6. Conclusions

In the subset selection problem, all-possible regression or exact algorithms, such as branch-and-bound programming, obtain the global optimum, but their computational feasibility diminishes for a large number of variables (p > 40) due to long processing times. Simple heuristic methods, often used in statistical SAS programs, include forward selection, backward elimination, and stepwise regression methods. Their computing time is fast, but solution quality is generally poor.

In general, metaheuristic methods provide better solution quality than simple heuristics. In the subset selection problem, two typical metaheuristic methods, TS and hybrid GSA, have been used. However, these two methods have shortcomings. The tabu search method requires a large amount of computing time, due to many neighborhood moves, and the hybrid GSA method produces a less accurate solution.

To overcome the shortcomings of these methods, an improved tabu search (ITS) was developed to reduce moves of the neighborhood and to adopt an effective search strategy for the neighborhoods. To evaluate the performance of the proposed ITS method, comparative analytical tests were performed on small literature data sets and on large simulation data sets. Computational results showed that the proposed method outperforms the previous metaheuristics in terms of the computing time and solution quality.

References

• I. Guyon, and A. Elisseeff, “An introduction to variable and feature selection”, Journal of Machine Leaning Research, 3, p1157-1182, (2003).
• G. M. Furnival, and R.W. Wilson, “Regression by leaps and bounds”, Technometrics, 16, p416-423, (1974). [https://doi.org/10.1080/00401706.1974.10489231]
• A. P. D. Silva, “Efficient variable screening for multivariate analysis”, Journal of Multivariate Analysis, 76, p35-62, (2001). [https://doi.org/10.1006/jmva.2000.1920]
• A. P. Duarte-Silva, “Discarding variables in a principal component analysis: algorithms for all-subsets comparisons”, Computational Statistics, 17, p251-271, (2002). [https://doi.org/10.1007/s001800200105]
• C. Gatu, and E. J. Kontoghiorghes, “Branch-and-bound algorithms for computing the best-subset regression models”, Journal of Computational and Graphical Statistics, 15(1), p139-156, (2006). [https://doi.org/10.1198/106186006X100290]
• M. Hofmann, C. Gatu, and E. J. Kontoghiorghes, “Efficient algorithms for computing the best subset regression models for large-scale problems”, Computational Statistics and Data Analysis, 52(1), p16-29, (2007). [https://doi.org/10.1016/j.csda.2007.03.017]
• M. J. Brusco, D. Steinley, and J. D. Cradit, “An exact algorithm for hierarchically well-formulated subsets in second-order polynomial regression”, Technometrics, 51(3), p306-315, (2009). [https://doi.org/10.1198/tech.2009.08022]
• J. Pacheco, S. Casado, and S. Porras, “Exact methods for variable selection in principal component analysis: Guide functions and pre-selection”, Computational Statistics and Data Analysis, 57(1), p95-111, (2013). [https://doi.org/10.1016/j.csda.2012.06.014]
• Z. Drezner, and G. A. Marcoulides, “Tabu seach model selection in multiple regression analysis”, Communications in Statistics – Simulation and Computation, 28(9), p349-367, (1999). [https://doi.org/10.1080/03610919908813553]
• H. Hasan, “Subset selection in multiple linear regression models: A hybrid of genetic and simulated annealing algorithms”, Applied Mathematics and Computation, 219(23), p11018-11028, (2013). [https://doi.org/10.1016/j.amc.2013.05.016]
• N. R. Draper, and H. Smith, Applied Regression Analysis, 3th Edition, NewYork, Wiley, (1998). [https://doi.org/10.1002/9781118625590]
• D. G. Montgomery, and E. A. Peck, Introduction to Linear Regression Analysis, 2nd Edition, NewYork, Wiley, (1992).
• F. Glover, “Heuristics for integer programming using surrogate constraints”, Decision Sciences, 8(1), p156-166, (1977). [https://doi.org/10.1111/j.1540-5915.1977.tb01074.x]
• F. Glover, “Future paths for integer programming and links to artificial intelligence”, Computers and Operations Research, 13(5), p533-549, (1986). [https://doi.org/10.1016/0305-0548(86)90048-1]
• S. Oliveira, and G. Stroud, “A parallel version of tabu search and the assignment problem”, Heuristics for Combinatorial Optimization, 4, p1-24, (1989).
• D. D. Werra, and A. Herz, “Tabu search techniques: a tutorial and an application to neural networks”, OR Spektrum, 11, p131-141, (1989). [https://doi.org/10.1007/BF01720782]
• M. Laguna, J. W. Barnes, and F. Glover, “Tabu search methods for a single machine scheduling problem”, Journal of Intelligent Manufacturing, 2(2), p63-74, (1991). [https://doi.org/10.1007/BF01471219]
• M. Laguna, and J. L. G. Velarde, “A search heuristic for just-in-time scheduling in parallel machines”, Journal of Intelligent Manufacturing, 2(4), p253-260, (1991). [https://doi.org/10.1007/BF01471113]
• J. A. Bland, and G. P. Dawson, “Tabu search and design optimization”, Computer Aided Design, 23(3), p195-202, (1991). [https://doi.org/10.1016/0010-4485(91)90089-F]
• F. T. Lin, C. Y. Kao, and C. C. Hsu, “Applying the genetic approach to simulated annealing in solving some NP-hard problems”, IEEE Transactions on System Man Cybernetics, 23(6), p1752-1767, (1993). [https://doi.org/10.1109/21.257766]
• J. H. Holland, “Adaptaion in natural and artificial systems”, University of Michigan Press, (1975).
• S. Kirpatirck, C. D. Gelatt, and M. P. Vecchi, “Optimization by simulated annealing”, Science, 220, p671-680, (1983). [https://doi.org/10.1126/science.220.4598.671]
• M. Widmer, and A. Hertz, “A new heuristic method for the flow shop sequencing problem”, European Journal of Operational Research, 41(2), p186-193, (1989). [https://doi.org/10.1016/0377-2217(89)90383-4]
• E. Tailard, “Some efficient heuristic methods for the flow shop sequencing problem”, European Journal of Operational Research, 47(1), p65-74, (1990). [https://doi.org/10.1016/0377-2217(90)90090-X]