CFD analysis of the effect of different PAR locations against hydrogen recombination rate

1. Introduction

The potential danger of hydrogen was first identified after the Three Mile Island accident in 1989, where a large quantity of hydrogen was released into the containment and started to combust. Since then, numerous studies focusing on mitigating and reducing the potential risk of a hydrogen explosion have been conducted. The recent hydrogen explosions that occurred during the Fukushima Daiichi accident in March 2011 showed that the control and mitigation of risk of a hydrogen explosion are still key safety issues for nuclear power plants [1].

During a loss of coolant accident (LOCA), hydrogen gas may accumulate within the containment of a nuclear power plant. The hydrogen can be generated from (i) a metal-water reaction involving the zirconium fuel cladding and the reactor coolant, (ii) the radiolytic decomposition of water, which also produces oxygen, and (iii) the corrosion of the construction materials [2]. Hydrogen is then induced into the reactor coolant system, and gradually, the entire containment. Assuming the internal conditions of the containment, such as the quality of the steam and air present, a flammable gas mixture may combust, generating a chemical and thermal load with a potential threat to the integrity of the containment [3]-[5].

A catalytic reaction is widely used owing to its lower threshold temperature required for a spontaneous reaction compared to that of a non-catalyzed reaction. Passive autocatalytic recombiners (PARs) are currently implemented in many modern pressurized water reactors (PWRs) as an engineered safety feature for mitigating risk in the event of a core melt-down accompanied by significant releases of hydrogen gas into the reactor containment [6][7]. The catalyst materials are made of platinum and/or palladium, and recombine the hydrogen and oxygen gases into a water vapor upon contact with the surface of the catalyst. Hence, the heat produced during the recombination process creates a strong buoyancy effect, which increases the influx of surrounding gases into the inlet of the PAR [8].

Catalysts are generally developed in the shape of a plate or pellet. For example, PAR manufacturers such as AREVA and AECL utilize a plate-type catalyst, whereas NUKEM developed a specialized cartridge containing pellet-type catalysts. KNT developed a distinctive PAR model with enhanced hydrogen- removal capabilities. The new catalyst model adopts a larger surface area and the characteristics required to enhance the buoyancy-induced convective flow.

Korea Nuclear Technology (KNT) developed a PAR model with enhanced hydrogen removal capabilities. This new model adopts the shape of a honeycomb to create a greater catalyst surface area and an enhancement of the buoyancy-induced convective flow [9]. The KNT PAR is a stainless housing equipped with catalysts inside the lower part of the box. The design of the nuclear containment may cause some of the hydrogen to become trapped in the containment and unable to be reduced using mitigation equipment. Therefore, the location where the PAR is installed will indirectly affect its performance. Hence, a residual amount of hydrogen in a nuclear power plant will accumulate and become a potential risk for a future hydrogen explosion. To investigate and compare the differences in hydrogen reduction, this study proposes the PARs be installed at different locations within the nuclear containment.

2. Mathematical modeling

This study involves the use of Computational Fluid Dynamics (CFD), which is a widely used computer-based tool for analysis and the design process. By utilizing the advances in computing power and graphics, the creation and analysis of a certain model is much less labor intensive and cheaper than applying experimental methods.

ANSYS CFX solves the unsteady Navier-Stokes equation in its conservation form. The instantaneous equation of mass (continuity) in a stationary frame is expressed as the following equation:

In addition, the instantaneous equation for momentum is expressed as follows:

These instantaneous equations are averaged for turbulent flows leading to additional terms that need to be solved. Whereas the Navier-Stokes equations describe both laminar and turbulent flows without additional terms, realistic flows involve length of scales much smaller than the smallest finite volume mesh. A direct numerical simulation of these flows requires significantly more computing power than what is available now or will be available in the near future.

Therefore, a significant amount of research has been conducted on predicting the effects of turbulence using turbulence models. Such models account for the effects of turbulence without the use of a very fine mesh or a direct numerical simulation.

These turbulence models modify the transport equations by adding in the averaged and fluctuating components. The transport equations have been modified into the following two equations.

The mass equation has not been modified, but the momentum equation contains extra terms, i.e., the Reynolds stresses, $$ \overline{\rho u\otimes u}$$, and the Reynolds fluxes, $$ \overline{\rho u\otimes }$$. These Reynolds stresses were previously modeled through additional equations to obtain closure. Obtaining closure implies applying equations to obtain closure, and that there is a sufficient number of equations to solve all of the unknowns including the Reynolds stresses and Reynolds fluxes.

Various turbulence models provide various ways to obtain closure. The model utilized in this investigation is the Shear Stress Transport (SST) model. The advantage of using this model is that it combines the advantages of other turbulence models (k-ε, Wilcox k-ω, and BSL k-ω).

The characteristic of the Wilcox model is the strong sensitivity to free-stream conditions. Therefore, a blending of the k- ω model near the surface and the k-ε model in the outer region was achieved by Menter, which resulted in the formulation of the BSL k-ω turbulence model. This model consists of a transformation of the k-ε into a k-ω formulation, subsequently adding in the resulting equations. The Wilcox model is multiplied by a blending function, F1, and transformed k-ε using another function, 1-F1. F1 is a function of the wall distance (a value of 1 near the surface and zero outside the boundary layer). The standard k-ε model is used outside and at the edge of the boundary layer.

However, whereas the BCL k-ω model combines the advantages of both the k-ε and Wilcox k-ω turbulence models, it fails to properly predict the onset and amount of flow separation from a smooth surface. The k-ε and Wilcox k-ω turbulence models do not account for the transport of turbulent shear stress resulting in an over-prediction of the eddy viscosity. A limiter on the formulation can be used to obtain the proper results. Such limiters are given in the following equation:

Where $$ V_t=\frac{{\upsilon }_t}{\rho }$$

F2 is a blending function that restricts the limiter to the wall boundary, and S is an invariant measure of the strain rate.

The blending functions are given through the following two equations:

where y is the distance to the nearest wall, and v is the kinematic viscosity. In addition,

3. KNT PAR Calculations

3.1 Mesh and conditions

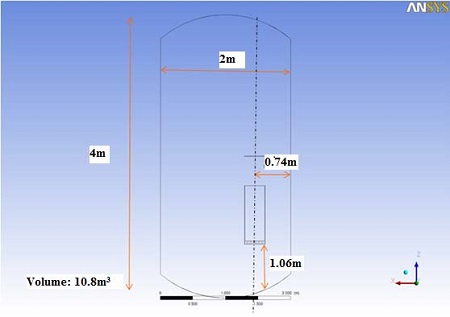
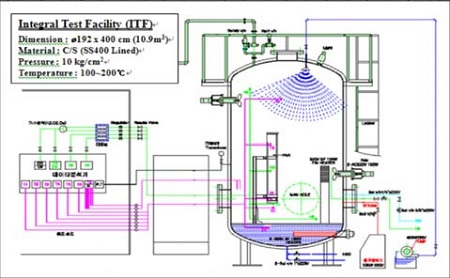
A mesh with a ratio of 1:1 was designed by referring to the size of the KNT PAR, which referred to the research paper (Figure 1). To validate the actual size of the designed mesh PAR with the real KNT PAR, a test was conducted and the results were compared with the data provided by KNT. A simulation was created according to the actual size of the KNT integral test facility (ITF). The input conditions of the test were more or less similar to the information obtained from KNT. Therefore, we were able to determine the working properties of the mesh. Figure 2 shows a conceptual diagram of the ITF. The ITF comprises a carbon steel pressure vessel with an internal volume of 10.8 m³. It was constructed to conduct performance tests under varying conditions of pressure, temperature, humidity, hydrogen concentration, and water spray. It has a cylindrical shape ~2.0 m in diameter by ~4.0 m in height. Safety and relief valves are installed on the top of the pressure vessel for the purpose of pressurization protection and venting, respectively. A manhole and penetration ports are installed on the side for the instrumentation and the injection of air and hydrogen, respectively. All components are composed of stainless steel piping and are sealed tight under high pressure.

Figure 1:

Conceptual diagram of KNT honeycomb model integral test facility (ITF)

Figure 2:

Actual conceptual diagram of KNT integral test facility

3.2 Results

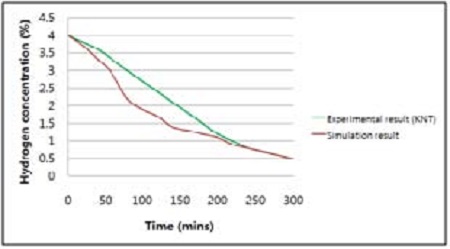
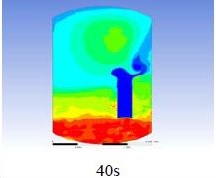
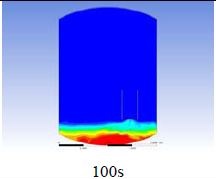
The Table 1 shows the results of the KNT PAR simulation. The movement of the gases within the containment was in a swirling direction, and most of the hot steam was accumulated at the top of the containment. The recombination process was continuously applied throughout the experiment, but a small amount of hydrogen accumulated at the bottom part of the containment. The hydrogen in the containment was successfully reduced from 4%, which is the lower flammability limit, and the rest was assumed to be oxygen. The experimental result was found have a slightly higher recombination rate compared to the KNT PAR, but still reached the same result at the end of the simulation as shown in Figure 3.

Table 1:

Hydrogen reduction fraction contour of KNT PAR simulation result (cut plane)

Figure 3:

Hydrogen reduction rate comparison

4. PAR Installed Locations

4.1 Conditions and mesh

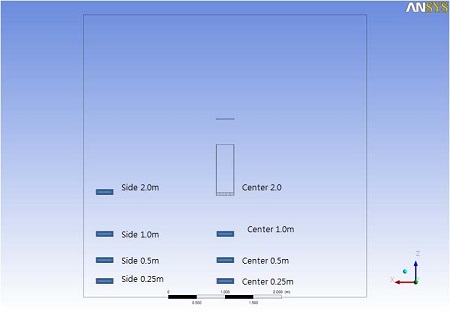
The nuclear containment adopted in this study was merely a square cube, 5 m in length, 5 m in width, and 5 m in height. The KNT PAR was then placed at the center of the containment, 2 m from the bottom, as the default location (Figure 4). There were only two types of gas in the containment. The hydrogen volume fraction was set to the lower flammability limit of 4%, and the rest was assumed to be oxygen.

Figure 4:

Different locations where the PAR model was installed

Adiabatic conditions were chosen for the test conditions, which ignore the heat transfer into the compartment walls and any condensation that would result in a mixing of the atmosphere. Test conditions and mesh details are shown in Table 2 and Figure 5 and 6.

Table 2:

Simulation test input condition

Figure 5:

CFX mesh of KNT PAR

Figure 6:

Meshes of the KNT PAR and the containment

4.2 Results and discussion

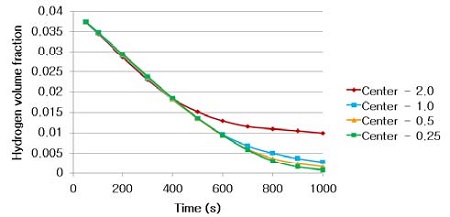
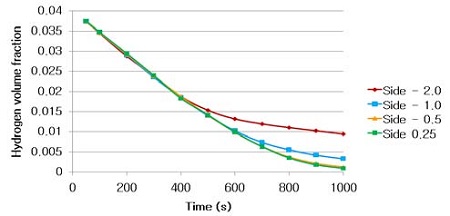
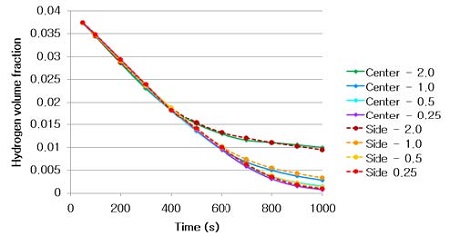
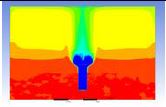
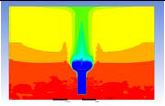
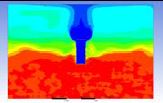
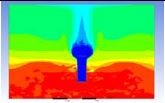
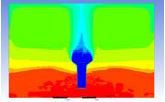
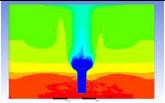
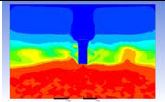
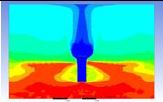
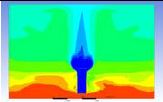
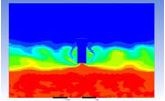
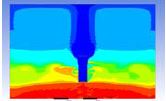
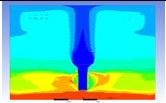
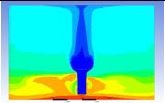
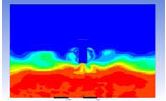
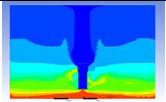
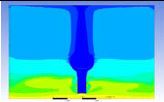
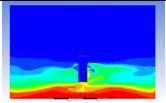
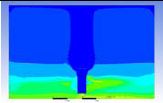
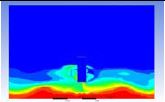
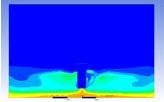
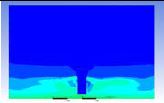
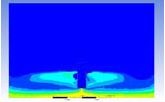
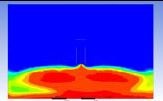
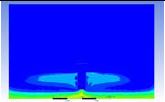
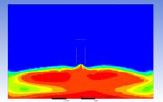
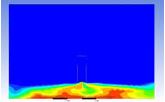
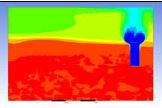
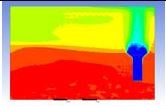
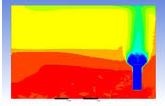
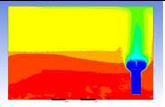
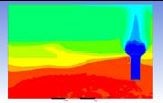
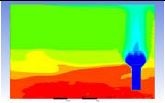
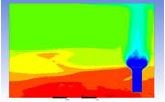
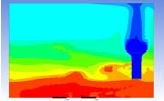
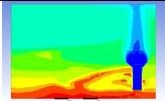
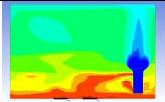
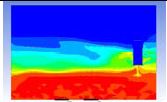
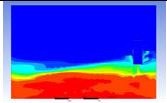
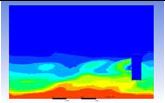
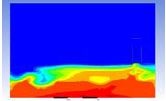
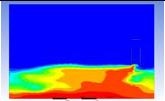
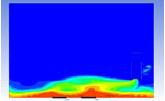
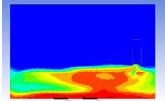
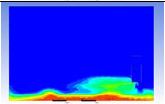
Table 3 and 4 above show the hydrogen reduction changes in the nuclear containment from 0 s up to 1,000 s. The PARs were installed at two different locations and at different heights from the hydrogen gas induction source.

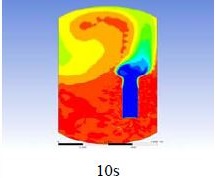
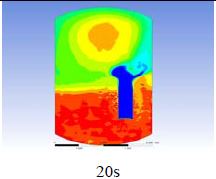
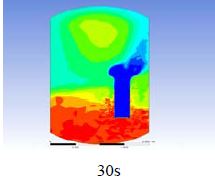
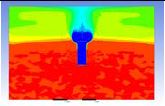
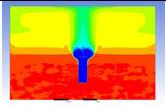
The diagrams above show the hydrogen reduction up to 1,000 s. The red color represents the original concentration of hydrogen gas, which is the lower flammability limit of 4%, and the blue color represents the hydrogen gas concentration after reduction, which is 0.5%. As the observation of the hydrogen concentration changes in the PAR, the concentration of hydrogen gas underwent a reduction and was removed. However, some residual hydrogen gas remained in the containment, which is represented by the red color. We could see that the container in which the PAR was installed 2.0 m from the inlet had the greatest amount of residual hydrogen gas. The container in which the PAR was installed at the bottommost case also had the least amount of residual hydrogen gas.

Table 3:

Hydrogen concentration variation with inlet location in the case of center placed

Table 4:

Hydrogen concentration variation with inlet location in the case of side placed

As shown in Figure 7 and 8, the average amount of hydrogen gas in the nuclear containment was reduced to 75% of the original concentration. However, in the cut plane of the nuclear containment, a large amount of hydrogen gas remained at the bottom.

Figure 7:

Results of PAR installed at the center of the containment

Figure 8:

Results of PAR installed at the side of the containment

Based on the results, we can conclude that a correlation exists between the locations where the PAR is installed and the hydrogen reduction rate. If the PAR is installed at a location farther from the hydrogen induction source, a greater amount of residual hydrogen gas will remain. In contrast, if the PAR is installed at a location closer to the hydrogen induction source, less residual hydrogen gas will remain at the end of the test. Owing to the buoyancy-induced force, the hydrogen gas remaining under the inlet of the PAR is difficult to reduce from the containment.

Figure 9:

Comparison of hydrogen reduction curves

The accumulation of hydrogen gas at the bottom of the containment was to a certain degree caused by the assumption of adiabatic walls. In a real scenario, the heat transfer to the compartment walls and the condensation would result in an enhanced mixing of the atmosphere.

Nevertheless, the residual amount of hydrogen gas in the containment can never be ignored. The high concentration of hydrogen gas was above of the lower flammability limit of 4%. If this residual amount of hydrogen gas were to remain and not be removed from the containment, it would become a risk factor for a future hydrogen explosion. For a real accident taking place in a nuclear power plant, the consequences could be significant. Owing to the complicated and irregular shape of the internal structures, more residual hydrogen may remain in the containment and may not be removable.

However, the differences in the results between the PAR installed at the center and at the side of the containment at the same height were not significant.

5. Conclusions

The hydrogen recombination rate was concluded to be proportional to the distance to the hydrogen induction location. A PAR installed at a bottom location (nearer the hydrogen induction source) has a better hydrogen recombination rate compared to a PAR installed at a higher location, whereas a PAR installed at the center of the containment does not show a significant difference in the hydrogen recombination rate compared to a PAR installed at the side of the containment.

Acknowledgments

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government(MSIP) (No. 2012M2A8A4025897).

References

• J. H. Song, and T. W. KIM, “Severe Accident Issues Raised by the Fukushima Accident and Improvements suggested”, Nuclear Engineering and Technology, 46(2), (2012). [https://doi.org/10.5516/NET.03.2013.079]
• R. G. Gido, COGAP: A Nuclear Power Plant Containment Hydrogen Control System Evaluation code, NUREG/CR-2847; LA-9459-MS ON: DE83006406, Los Alamos National Lab, NM, USA, (1983).
• W. Breitung, and P. Royl, “Procedure and tools for deterministic analysis and control of hydrogen behavior in severe accidents”, Nuclear Engineering and Design, 202(2-3), p249-268, (2000). [https://doi.org/10.1016/S0029-5493(00)00380-0]
• E. Bachellerie, F. Arnould, M. Auglaire, B. De Boeck, O. Braillard, B. Eckardt, F. Ferroni, and R. Moffett, “Generic approach for designing and implementing a passive autocatalytic recombiner PAR-system in nuclear power plant containments”, Nuclear Enginnering and Design, 221(1-3), p151-165, (2003). [https://doi.org/10.1016/S0029-5493(02)00330-8]
• S. J. Han, and K. I. Ahn, “An investigation of potential risks of nuclear system from hydrogen production”, Nuclear Engineering and Design, 270, p119-132, (2014). [https://doi.org/10.1016/j.nucengdes.2013.12.054]
• E. A. Reinecke, I. M. Tragsdorf, and K. Gierling, “Studies on innovative hydrogen recombiners as safety devices in the containments of light water reactors.”, Nuclear Engineering and Design, 230(1), p49-59, (2004). [https://doi.org/10.1016/j.nucengdes.2003.10.009]
• J. Deng, and X. W. Cao, “A study on evaluating a passive autocatalytic recombiner PAR-system in the PWR large-dry containment”, Nuclear Engineering and Design, 238(10), p2554-2560, (2008). [https://doi.org/10.1016/j.nucengdes.2008.04.011]
• C. Appel, I. Mantzaras, R. Schaeren, R. Bombach, and A. Inauen, “Catalytic combustion of hydrogen-air mixtures over platinum: validation of hetero/homogenous chemical reaction schemes”, International Journal of Energy for a Clean Environment, 5(1), (2004). [https://doi.org/10.1615/interjenercleanenv.v5.i1.20]
• J. W. Park, B. R. Koh, and K.Y. Suh, “Demonstrative testing of honeycomb passive autocatalytic recombiner for nuclear power plant”, Nuclear Engineering and Design, 241(10), p4280-4288, (2011). [https://doi.org/10.1016/j.nucengdes.2011.07.040]