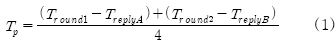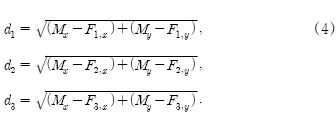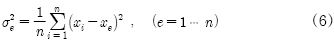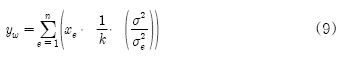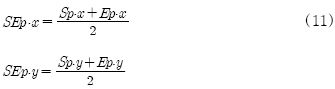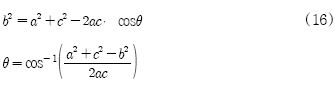A study on indoor navigation system using localization based on wireless communication
Recently, navigation systems based on wireless communication have been applied to the internal structures such as building or ship. If a stable azimuth information is obtained, these systems can effectively guide the direction of the user's progress through the information and then can improve the performance of guidance. Since conventional method which has acquired an azimuth information using geomagnetic and acceleration sensor(azimuth sensor hereafter) is sensitive to the effects of the magnetic field, it has unstable error range according to the surrounding environment. In order to improve these problems, this paper presents a new relative azimuth estimation algorithm using the displacement of a mobile node and its rotation angle based on Wireless communication. For the performance assessment of the proposed algorithm, experiments using rotating arm are performed and the results are confirmed that the proposed system can estimate the relative azimuth without using additional sensors.
초록
최근 무선통신기반 내비게이션 시스템이 건물이나 선박과 같은 구조물의 내부에 적용되고 있다. 이러한 시스템이 안정된 방위각 정보를 얻는다면 이를 통하여 사용자의 진행 방향을 효과적으로 안내 할 수 있고 그에 따른 안내 성능을 향상시킬 수 있다. 기존의 방법은 지자기 및 가속도 센서(이하 방위각센서)를 이용하여 방위각 정보를 획득하므로 이는 자계의 영향에 민감하여 주위환경에 따라 불안정한 오차 범위를 가진다. 이러한 문제점을 개선하기 위하여 본 논문에서는 무선통신기반 이동노드의 변위와 회전각을 이용하여 새로운 상대방위각 추정 알고리즘을 제안한다. 제안한 알고리즘의 성능을 평가하기 위해 회전팔을 이용한 실험을 수행하였으며 그 결과 부가적인 센서를 이용하지 않고 상대방위각을 추정할 수 있음을 확인하였다.
Keywords:
Navigation, Wireless communication, Localization, Azimuth, 내비게이션, 무선통신, 위치인식, 방위각1. 서 론
유비쿼터스 센서 네트워크(Ubiquitous Sensor Networks, USN) 기술은 인간의 삶을 윤택하게 함에 따라 더욱 다양한 분야에 접목되기 위하여 지속적으로 연구되고 있다. 그중 위치인식 기술의 대표적인 예로써 GPS(Global Positioning System)를 활용한 내비게이션 시스템은 선박, 항공, 자동차 및 일반 보행자를 위해 경로 안내를 목적으로 매우 이롭게 사용되고 있다[1]. 실외뿐만 아니라 건물 구조물의 실내에서 내비게이션 시스템을 적용시키기 위하여 무선통신, 영상매칭, 센서 등을 활용한 실내 위치인식 방법들이 끊임없이 연구되고 있다. 최근 Cho 외[2]는 IEEE 802.15.4a Chirp 신호를 기반으로 사용자에게 부착된 센서를 통하여 보폭 측정 알고리즘을 이용하는 실내 위치인식 시스템을 연구하였고, 스마트폰이 대중화됨에 따라 WiFi(Wireless Fidelity)를 활용하여 대형 백화점에서 사용할 수 있는 실내용 내비게이션 어플리케이션이 실제로 운용되고 있다[3]. 이러한 내비게이션의 최적경로안내는 위치인식뿐만 아니라 방위각정보를 통하여 사용자가 다음에 진행하여야 할 방향을 효과적으로 안내할 수 있고, 이에 따라 기존에는 방위각센서를 활용하여 방위각을 추정하는 방법들을 주로 사용하고 있다.
Lee 외[4]는 소형 관성센서 및 초음파속도계를 이용하여 잠수정의 수중 복합항법 시스템을 구현하고 실험하였으며, 그 결과 기존의 방위각센서에 비해 개선된 성능을 검증하였다. Shin 외[5]는 관성센서를 이용하여 보행자의 항법시스템을 연구하고 방위각센서를 통하여 이동경로에 따른 맵 매칭 기법을 개발하였다. Jung 외[6]는 항공기의 항법시스템 연구 중 교차로의 위치 및 지선별 방위각이 저장된 데이터베이스를 구축하고 카메라 영상정보의 매칭을 통하여 방위각을 획득할 수 있음을 확인하였다. 하지만 이러한 방법들은 수중 또는 육상의 넓은 실외 공간에 적용되기 위한 방법들이며 실내 환경을 고려하지 않고 수행된 연구결과이다. 철골 구조와 좁은 통로들로 이루어진 선박 구조물의 특수한 실내 환경에서 방위각센서가 사용될 경우 제한된 공간 및 전자기적 잡음 등에 의하여 안정된 방위각을 획득하기 어려운 상황이 발생할 수 있고, 이를 해결할 수 있는 대안이 부족한 실정이다.
따라서 본 논문은 자계 또는 전기적 잡음으로 인하여 방위각센서로부터 방위각의 획득이 어려운 상황에서 무선통신기반 이동노드의 변위정보와 이를 통한 회전각 예측을 이용하여 새로운 상대방위각 추정 알고리즘을 제안한다. 본 연구의 알고리즘은 이동노드가 임의의 반경으로 원호를 그리며 변위한다는 가정 하에 적용이 가능하며, 이동노드의 좌표데이터를 기반으로 중심축을 선정 후 원호의 시작점, 끝점, 중심축의 세 점을 통하여 회전각을 얻고 이에 따라 상대방위각을 추정 할 수 있다. 성능을 확인하기 위한 실험은 근거리 무선통신이 가능한 3개의 고정노드 및 1개의 이동노드를 사용하고, 이동노드가 원호를 그리며 회전 할 수 있도록 회전팔을 제작하여 실험을 수행하였다. 회전팔의 실제 회전각과 제안한 알고리즘을 통해 추정된 회전각을 비교 및 분석하여 그 성능을 입증하였다. 또한 모바일 노드의 위치인식 데이터 중 잡음성분을 효과적으로 제거하기 위하여 변형된 가중치 평균필터를 적용하여 효율적 평균을 취함으로써 상대방위각 추정의 정확도를 높일 수 있음을 확인하였다.
2. 위치인식 관련이론 및 UWB 성능
2.1 SDS-TWR과 삼변측량법
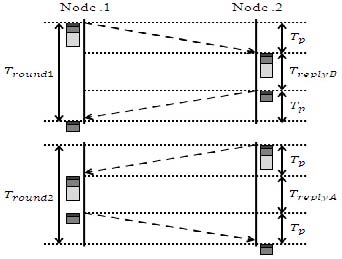
TOF(Time of Flight)기반의 두 노드 간 거리측정을 위한 SDS-TWR(Two Way Ranging)은 Figure 1과 같은 절차를 수행한다. Node.1은 패킷송신의 시작시간을 저장한 후 전송하고, Node.2는 패킷수신의 시작시간을 저장한다. Node.2는 TreplyB만큼 대기한 후, 패킷송신의 시작시간을 저장한 후 전송하고, Node.1은 패킷수신의 시작시간을 저장한다. 이를 총 2회 반복함으로써 전파도달시간의 오차를 줄이게 되며, 전파도달 시간(Tp)은 식 (1)과 같다.
전파의 속도(C)는,
C = 3.18 × 1010cm/s (2)
로 표현될 때, 두 노드간의 거리(Distance)는 전파가 도달하는데 걸린 시간(Tp)과 전파속도(C)의 곱으로써 표현 될 수 있으며, 이는 식 (3)과 같다.
Distance = Tp × C (3)
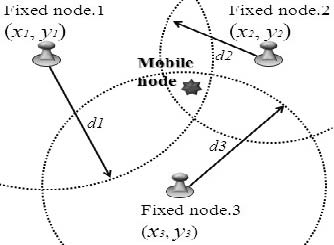
이동노드 위치는 SDS-TWR을 이용하여 3개 이상의 고정노드로부터 거리측정값을 획득한 후 Figure 2의 삼변측량법을 이용하여 나타낼 수 있다. 이동노드의 위치를 (Mx, My)라 하고, 고정노드의 위치를 (Fn,x,Fn,y)라 할 때 각 고정노드로부터의 거리측정값(dn)은
로 표현된다. 여기서 d1은 고정노드1과 이동노드와의 거리, d2는 고정노드2와 이동노드와의 거리, d3는 고정노드3과 이동노드와의 거리를 나타낸다. Figure 2와 같이 각 고정노드의 위치를 원점으로 하고 d1, d2, d3를 반지름으로 하는 원이 그려지면 최대 6개의 교점이 존재할 수 있고, 내부에 근접한 3개의 교점을 찾고 그 중심에 이동노드가 위치한다고 인식할 수 있다.
2.2 UWB의 위치인식 성능
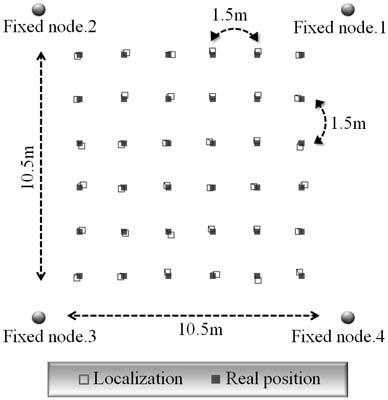
임펄스를 사용하는 IEEE 802.15.4a기반 UWB는 비교적 정밀한 거리측정이 가능하고, 벽면이 존재하는 실내의 멀티패스 환경에서 안정적인 오차범위를 가지는 것으로 알려져 있다. UWB의 실직적인 2차원 위치인식 성능을 확인하기 위하여 실외의 자유공간에서 고정노드 4개와 이동노드 1개를 사용하여 실험을 수행한 결과는 Figure 3과 같다. 고정노드의 간격은 10.5m로 하고 이동노드의 실제위치를 1.5m마다 변경하며 실험한 결과 평균 오차는 약 0.12m로 나타났으며, 중앙 및 외곽부분의 오차의 크기가 일정함에 따라 고정노드와 이동노드의 거리에 관계없이 안정적인 위치인식이 가능함을 확인하였다. 한편, 제조사의 제조기술에 따라 거리측정 성능이 차이가 있으므로 절대적인 UWB의 성능이라고 말할 수 없을 것이며, 이 실험을 수행하기 위하여 Time domain사의 P410RCM모듈을 이용하였고, 이 모듈은 TOF기반 SDS-TWR을 이용하여 노드 간 거리측정값을 제공한다.
3. 제안한 상대방위각 추정 알고리즘
3.1 변형된 가중치 평균필터
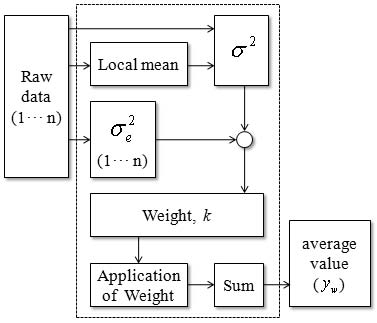
본 논문에서 제안한 알고리즘은 적응형 메디안 필터[7]를 본 연구에 알맞게 개선하여 Figure 4의 절차를 수행하는 변형된 가중치 평균필터를 통하여 잡음성분을 제거 한 후 상대방위각을 추정하게 된다. 이 중 내재적 오차를 지닌 Raw data에서 잡음을 얼마나 효과적으로 제거하는가에 따라 상대방위각의 정확도에 큰 영향을 미치므로 이 전처리 과정은 매우 중요하다. 따라서 Raw data에서 오차의 크기에 따라 가중치를 다르게 적용하여 효율적 평균을 취함으로써 임펄스 잡음을 효과적으로 제거하는 변형된 가중치 평균필터는 다음과 같이 전개된다.
일반적으로 모분산(σ2)은
로 나타내고, 여기서 n은 측정치 개수, xi는 i번째 측정치, m은 측정치들의 평균이다. 이를 변형한 개념으로 e번째 측정치를 기준으로 분산을 나타내는 원소값분산(σ2e)은
이라 하고, 여기서 xe는 원소값(e번째 측정치)을 나타낸다. σ2e이 클수록 원소값은 잡음적 특성을 강하게 나타내는 것이므로
을 통하여 잡음의 크기는 0에서 1까지의 수치로 표현된다. 식 (7)의 c가 0에 가까울수록 잡음적 특성이 강하며, 1에 가까울수록 잡음적 특성이 약하다고 할 수 있다. c의 크기에 따라 각 측정치에 가중치를 부여하기 위하여 가중치의 총합(k)을 구하고, 이는
로 표현됨에 따라 변형된 가중치 평균필터가 적용된 최종 출력 값(yw)은
로 나타낸다. 입력된 Raw data는 제안한 필터를 취하여 잡음적 특성이 감소된 하나의 측정치로 표현될 수 있고, 이 가공된 데이터를 이용하여 다음 단계의 상대방위각 추정방법을 수행한다.
3.2 상대방위각의 추정방법
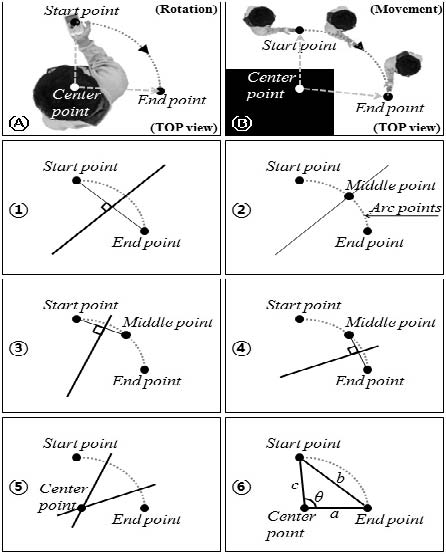
상대방위각 추정방법은 이동노드가 원호를 그리며 회전한다는 것을 가정하고 이는 Figure 5의 Ⓐ 및 Ⓑ에서 예시로 나타내고 있다. 이중 Ⓐ는 사용자가 이동노드를 손에 쥐고 제자리 회전을 하는 상황을, Ⓑ는 장애물을 우회하기 위해 원을 그리며 이동하는 상황을 보여준다.
제안한 알고리즘의 상대방위각 추정방법은 변형된 가중치평균필터를 통하여 가공된 데이터를 기반으로 Figure 5의 ①에서 ⑥까지의 과정으로 표현된다. ①단계는 회전을 시작한 점(Start point, Sp)과 회전을 끝내는 점(End point,SEp)를 선정하고, Sp와 Ep의 중간점(SE point, SEp)을 지나는 법선의 방정식을 얻는다.
Sp와 Ep를 지나는 직선의 방정식은
과 같고, 중간점의 좌표(SEp·x, SEp·y는
으로 나타낼 수 있다. 이를 통하여 SEp를 지나는 법선의 방정식은
의 방정식은
로 표현되고, 여기서
이다. ②단계는 이동노드가 원호를 그리며 변위된 위치인식 데이터(Arc points, Ap)에서 식 (12)를 지나는 직선에 포함된 점 또는 가장 가까운 점(Middle point, Mp)을 찾는 과정이다. 식 (12)에 Ap의 x좌표(APn·x)를 대입한
을 통하여 구해진 y의 값과 Apn의 y좌표(Apn,·y)의 차가 0 또는 최소인 Apn을 Mp로 선정하고, 이는 식 (15)로 표현된다.
다음과정은 ①단계에서 언급한 방법을 응용하여 ③단계는 Sp와 Mp를 지나는 직선에 그 중간점을 지나는 법선의 방정식을 얻고, ④단계는 Mp와 Ep를 지나는 직선에 그 중간점을 지나는 법선의 방정식을 얻는다. ⑤단계는 ③단계에서 얻어진 법선과 ④단계에서 얻어진 법선을 통하여 하나의 교차점(Center point, Cp)을 찾는다. ⑥단계는 Sp, Ep, Cp의 세 점을 통하여 각 변의 길이 a, b, c를 알 수 있고, 여기서 a와 c사이의 내각(θ)은 코사인 제2법칙에 의하여 식 (16)과 같다.
θ는 이동노드의 회전운동 변위에 대한 각도이므로 사용자가 이전에 응시하던 상대방위각에 θ를 합하여 현재 바라보고 있는 상대방위각을 추정할 수 있다.
4. 실험 및 결과분석
4.1 실험환경
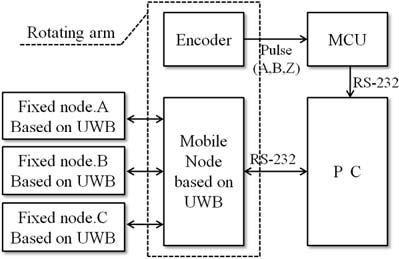
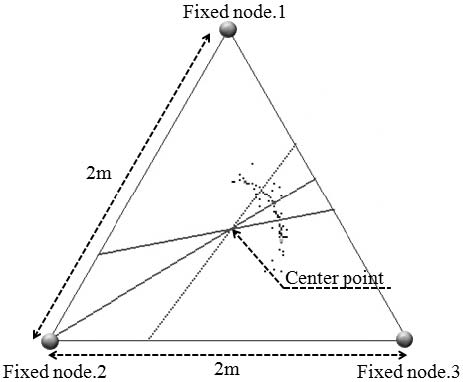
제안한 알고리즘의 상대방위각 추정성능을 확인하기 위하여 UWB기반으로 구성된 Figure 6과 Figure 7의 환경으로 실내공간에서 회전팔을 이용한 실험을 수행하였다. 3개의 고정노드는 한 변을 2m로 하는 정삼각형의 모서리에 위치시키고, 삼각형의 무게중심과 회전팔의 중심축이 같도록 설계하였다. 이 중심축에는 실제 회전한 각도를 획득하기 위한 360/500분해능의 엔코더가 설치되고, 반지름이 50cm인 회전팔의 끝부분에 이동노드가 설치되었다.
이동노드는 고정노드로부터 거리측정을 수행 후 RS-232 인터페이스를 통하여 PC로 측정데이터를 전송한다. PC는 Visual studio C#에서 개발된 모니터링 어플리케이션을 통하여 수신된 거리측정 데이터를 통해 삼변측량법 및 제안한 알고리즘을 연산하여 상대방위각을 추정한다. 또한, 엔코더로부터 A, B, Z상의 펄스를 입력받아 회전팔의 실제 각도를 계산하고 이 데이터를 PC로 송신하기 위해 8-bit MCU가 사용되었다.
4.2 실험결과 및 분석
Figure 7은 제안한 알고리즘을 수행하고, 3개의 법선과 Center point를 찾아낸 결과화면이다. 위치인식 좌표들은 원호를 그리며 비교적 정밀하게 나타나고 이에 따라 법선의 교차점인 Center point가 실제 회전팔의 중심축에 가깝게 추정되고 있음을 보인다.
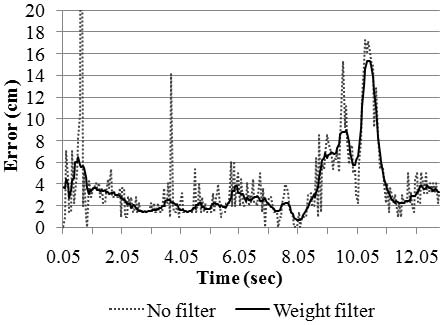
변형된 가중치 평균필터의 성능은 Figure 8과 같고, x축은 시간, y축은 오차의 크기, 점선은 필터가 적용되지 않은 Raw data, 실선은 필터가 적용된 데이터를 나타낸다. 이 실험은 이동노드가 한 위치에 정지된 상태에서 256개의 위치인식 데이터를 샘플링하여 제안한 필터의 적용전과 후를 그래프로 표현한 것이다. 이 필터를 통하여 평균적으로 약 6.38%의 오차가 개선되었고, 특히 임펄스 잡음을 효과적으로 감소시키는 특성을 확인할 수 있다. 따라서 이동노드 및 고정노드가 잡음 등의 영향을 받아 불안정한 상황에서 임펄스 특성의 위치가 인식 되었을 때 탁월한 성능을 발휘할 수 있을 것이다.
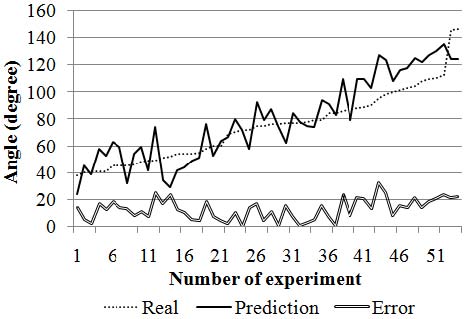
제안한 알고리즘의 성능은 Figure 9와 같고, 여기서 x축은 실험의 횟수, y축은 각도, 점선은 회전팔이 실제 회전한 각도, 실선은 제안한 알고리즘을 통하여 추정된 각도, 이중실선은 오차의 크기를 나타낸다. 실험횟수가 증가될수록 회전팔의 회전각은 최소 38˚에서 최대 146˚까지 변화시키며 실험이 수행되었다. 이 각도의 범위 내에서 추정된 회전각은 실제 회전각의 크기에 상관없이 32˚이하로 나타나는 오차를 나타내고 평균오차는 약 13˚이다. 회전팔의 반지름은 50cm이고 실제 회전각이 20˚이하일 때 이동노드가 원호를 그리며 이동한 위치인식 좌표데이터는 곡률이 매우 작은 원 또는 직선에 가까워지므로 추정되는 회전각의 오차가 크게 발생할 수 있는데, 이 원인은 회전팔의 반지름 대비 UWB기반 위치인식의 내재적 오차가 크다고 할 수 있기 때문이다. 따라서 회전팔의 실제 회전각이 작을 때는 회전팔의 반지름이 상대적으로 커야 오차의 범위를 줄일 수 있다. 본 실험에서 사용된 회전팔은 Figure 5의 Ⓐ와 같이 사용자가 이동노드를 손에 쥐고 제자리 회전을 하는 것을 감안하여 반지름을 비교적 짧게 하였으며, Figure 5의 Ⓑ와 같이 사용자가 장애물을 우회하거나 코너를 돌아 나아갈 때는 중심축이 사용자의 외부에 존재하므로 반경이 커지게 되어 추정되는 회전각의 오차는 감소한다. 따라서 제안한 알고리즘이 실내 내비게이션 시스템에 적용되었을 때 상대방위각 추정성능은 크게 향상될 것으로 기대한다.
5. 결 론
본 논문에서는 무선통신기반 위치인식 시스템을 사용할 경우 사용자가 소지한 이동노드의 변위정보를 통하여 상대방위각을 추정할 수 있는 알고리즘을 제안하였다. 반지름이 50cm인 회전팔을 이용하여 제안한 알고리즘을 실험한 결과 상대방위각 추정의 평균오차는 약 13˚를 나타내고 그 범위가 상대적으로 안정적임을 확인하였다. 이는 제안한 알고리즘을 통해 방위각센서를 이용하지 않고 위치인식으로부터 상대방위각을 추정하여 사용자가 진행해야 할 방향을 원활하게 안내 할 수 있음을 의미한다. 따라서 철골구조 및 복잡한 통로들로 구성되어 전자기적 잡음이 존재하는 선박이나 건물 등의 실내 환경에서 운용되는 내비게이션 시스템은 제안한 알고리즘을 통하여 안정적이며 효과적인 경로안내 성능을 발휘할 수 있을 것이다. 또한 UWB뿐만 아니라 CSS(Chirp Spread Spectrum), Zigbee, RFID(Radio Frequency Identification) 등의 다양한 위치인식 시스템에 적용될 수 있어 호환성이 높은 이점이 있다.
Acknowledgments
이 논문은 국토해양부의 지원으로 수행한 해양에너지 전문인력 양성사업 및 정부(교육과학기술부)의 재원으로 한국연구재단의 지원(No.20110029766)을 받아 수행한 연구결과입니다.
References
- K.-Y. Hwang, J.-M. Kang, and J.-D. Lee, “Developing a working navigator for street shoppers”, Journal of the Korean Society of Civil Engineers, 28(1D), p21-27, (2008).
-
H.-J. Cho, K.-I. Hwang, D.-S. Noh, and D.-H. Seo, “Real time indoor positioning system using IEEE 802.15.4a and sensors”, Journal of the Korean Society of Marine Engineering, 36(6), p850-856, (2012).
[https://doi.org/10.5916/jkosme.2012.36.6.850]

-
A. Mulloni, D. Wagner, I. Barakonyi, and D. Schmalstieg, “Indoor positioning and navigation with camera phones”, IEEE Pervasive Computing, 8(2), p22-31, (2009).
[https://doi.org/10.1109/MPRV.2009.30]

- C.-M. Lee, P.-M. Lee, S.-M. Kim, S.-W. Hong, J.-W. Seo, and W.-J. Seong, “Rotating arm test for assessment of an underwater hybrid navigation system for a semi-autonomous underwater vehicle”, Journal of the Korean Society of Ocean Engineers, 17(4), p73-80, (2003), (in Korean).
-
S.-H. Shin, H.-W. Kim, C.-G. Park, and S.-O. Choi, “Map-matching algorithm for MEMS-based pedestrian dead reckoning system in the mobile device", Journal of Institute of Control Robotics and System, 14(11), p1189-1195, (2008).
[https://doi.org/10.5302/J.ICROS.2008.14.11.1189]

- J.-H. Jung, J.-S. Yun, K.-Y. Choi, C.-K. Lyu, H.-S. Hwang, and S.-B. Kwon, “Image based navigation using geometry information of road", Proceedings of the Spring Conference of the Korean Society for Aeronautical and Space Sciences, p539-544, (2011), (in Korean).
- W.-Y. Cho, and D.-I. Choi, “Adaptive median filter by local variance and local central variance", Journal of the Institute of Electronics Engineers of Korea, 41sp(6), p285-294, (2004), (in Korean).