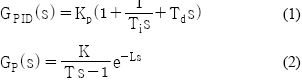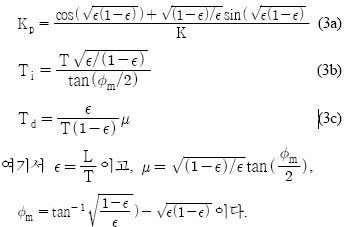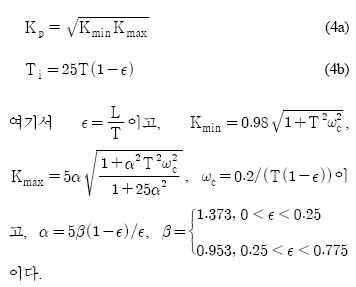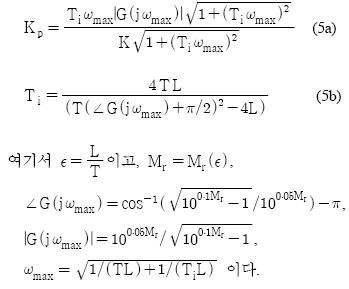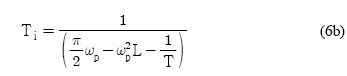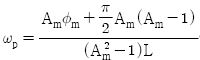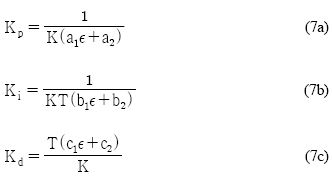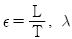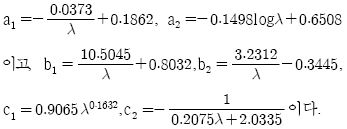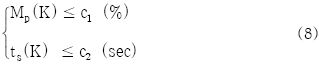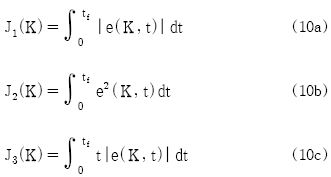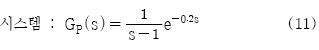[ Article ]

Journal of the Korean Society of Marine Engineering - Vol. 37, No. 1, pp.85-90

ISSN: 2234-7925 (Print) 2234-8352 (Online)

Print publication date Jan 2013

Received 26 Sep 2012 Revised 12 Nov 2012 Accepted 18 Jan 2013

DOI: https://doi.org/10.5916/jkosme.2013.37.1.85

RCGA-based PID control of unstable processes concerned with the constraints

LeeYun-Hyung¹ ; YangA-Young² ; SoMyung-Ok³ ; OhSea-Jun^†

1한국항만연수원 부산연수원 2(주)종합해사 부품팀 3한국해양대학교 기관공학부

제약조건을 고려한 불안정 시스템의 RCGA 기반 PID 제어

Correspondence to: ^†(606-080) 부산광역시 영도구 태종로 727 한국해양대학교 기관공학부, E-mail: sj505@hhu.ac.kr, Tel: 051-410-4285

PID control for unstable processes with time delay is not easy to apply because of unstability due to the poles existing on left-hand side in s-plane and the effect of time delay. In this paper, the authors consider the PID controller design technique in case of predefining overshoot or rising time by designer according to control environment. To deal with constraint problem like this, in this paper, the RCGA incorporating the penalty strategy is used. This is the method that if the RCGA violates given constraints, the defined penalty function is summed to the evaluation function depending on the severity and then the given constraint problem is converted to non-constraints optimization problem. The proposed method is applied to the unstable FOPTD(First Order Plus Time Delay) system and simulations are accomplished to illustrate the set-point tracking performance.

초록

시간지연을 갖는 불안정한 시스템의 PID 제어는 적용하기가 쉽지 않은데 이는 복소평면의 우반부에 존재하는 극점으로 인한 불안정성과 시간지연의 영향 때문이다. 본 연구에서는 설계자가 제어환경에 따라 오버슈트나 상승시간 등을 미리 정의한 경우의 PID 제어기 설계 기법에 대해 고려한다. 이와 같이 제약성을 갖는 최적화 문제를 해결하기 위해 본 연구에서는 벌점전략이 결합된 RCGA를 사용한다. 이는 제약조건을 위배하면 그 정도에 따라 벌점을 부가하도록 벌점함수를 정의하고, 평가함수에 합하여 비제약성 최적화 문제로 변환하는 방법이다. 제안하는 방법은 불안정 FOPTD 시스템에 적용하고 시뮬레이션을 실시하여 그 유효성을 검토한다.

Keywords:

Unstable FOPTD process, RCGA, Constraints, Penalty function, 불안정 FOPTD 프로세스, 제약조건, 벌점함수

1. 서 론

산업현장에서 확인할 수 있는 프로세스(Process)는 2차 이상의 고차 프로세스이면서 안정한 개회로 시스템이 대부분이다. 이러한 고차 시스템은 시간지연을 갖는 1차 시스템(First Order Plus Time Delay, FOPTD)으로 근사화가 가능하여 어렵지 않게 PID 제어기를 설계할 수 있다[1][2].

그러나 특정 시스템의 경우에는 시간지연과 s-평면상의 우반부에 특성근을 갖는 불안정한 프로세스도 존재한다. 본 연구에서는 특성근이 복소평면상의 우반부에 한 개 존재하며 시간지연도 함께 갖는 불안정한 FOPTD 프로세스를 고려하기로 한다. 이러한 프로세스는 특성근의 위치 때문에 근원적으로 불안정한 응답특성을 보일뿐만 아니라 안정한 시스템에서 획득할 수 있는 제어성능을 보장할 수 없어 PID 제어기 설계가 까다롭다.

불안정 FOPTD 프로세스의 PID 제어에 관한 기존의 연구로는 De Paor과 O'Malley[3]가 제안한 것으로서 지글러-니콜스(Ziegler-Nichols)방법을 개선하여 최적 이득여유와 최적 위상여유를 기반으로 하는 제어기법이 있다.

이후 Venkatashankar와 Chidambaram[4]에서는 De Paor와 O'Malley 방법에서 필요한 수치 해석적 방법 대신 근사적 해법을 이용해 P 제어기와 PI 제어기를, Poulin과 Pomerleau[5]에서는 최대 피크 공진에 기초한 PI 제어기와 PID 제어기를, Ho와 Xu[6]에서는 특정한 이득여유와 위상여유를 만족하도록 하는 PI 제어기를 제안하였다.

Wen과 Yingqin[7]에서는 루프-쉐이핑(loopshaping) 제어에 기초하여 PID 제어기를 동조하는 방법을 제안하였다. 그러나 이들 방법의 대부분은 이득 및 위상여유를 계산하는데 복잡한 수치 해석적 방법이 필요하다는 단점이 있다. 한편, Lee 외[8]에서는 실수코딩 유전알고리즘(Real-coded genetic algorithm : RCGA)을 이용하여 PID 제어기를 체계적으로 설계하는 방법을 제안하였다. 그러나 기존의 연구를 통해 얻어진 PID 제어기를 적용한 제어시스템은 시스템 특성상 모두 상당히 큰 오버슈트가 존재하는 응답특성을 보인다.

그러나 제어환경에 따라 설계자가 오버슈트 및 상승시간 등을 미리 설정하는 경우가 있을 수 있는데 이와 같은 경우 기존의 연구방법으로는 원하는 제어성능을 보장할 수 없다. 이는 기존의 연구에서는 이러한 제약조건을 고려하지 않기 때문이다.

따라서 본 논문에서는 제약 조건이 주어진 경우에 대해 PID 제어기 설계 기법을 제안하고자 하며 이를 해결하기 위해 벌점전략(Penalty strategy)이 결합된 RCGA를 사용하기로 한다. 이는 RCGA가 제약조건을 위배하면 그 정도에 따라 벌점을 부가하도록 벌점함수를 정의하고, 평가함수에 합하여 비제약성 최적화 문제로 변환하는 방법이다. 제안하는 방법은 시뮬레이션을 통해 기존의 방법과 비교하여 그 유효성을 검토한다.

2. 기존의 PID 제어기 동조법

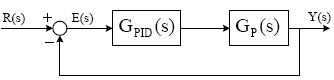
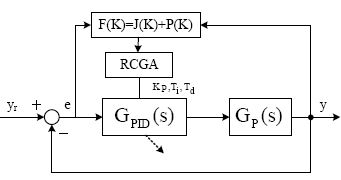
제어대상과 제어기가 결합된 블록선도는 Figure 1과 같으며 G_PID (s) 는 표준 PID 제어기로서 식 (1)과 같고, G_P (s) 는 불안정 FOPTD 프로세스로서 식 (2)와 같다.

Figure 1

Unit feedback PID control system.

여기서 K, T, L은 각각 시스템의 이득, 시정수와 시간지연을 의미한다.

2.1 De Paor와 O'Malley 방법

지글러-니콜스 방법을 개선한 것으로[3] 최적 이득여유와 최적 위상여유를 기반으로 하는 PID 제어기이며 제어기 파라미터는 식 (3)과 같다.

2.2 Venkatashankar와 Chikambaram 방법

De Paor과 O'Malley 방법에서 필요한 수치 해석적 방법 대신 근사적 해법을 이용해 P 제어기와 PI 제어기를 제안한 것으로[4] PI 제어기 파라미터는 식 (4)와 같다.

2.3 Poulin과 Pomerleau 방법

최대 피크 공진에 기초하여 PI 제어기와 PID 제어기를 제안하였으며[5] PI 제어기 파라미터는 식 (5)와 같다.

2.4 Ho와 Xu 방법

폐루프 시스템이 나이퀴스트(Nyquist) 안정도 조건을 만족시키는 것으로 특정한 이득여유와 위상여유를 만족하도록 하는 PI 제어기 설계기법이다[6]. 제어기 파라미터는 식 (6)과 같다.

여기서 이고, A_m과 ø_m은 사용자가 선정하는 이득여유와 위상여유를 의미한다.

2.5 Wen과 Yingqin 방법

루프-쉐이핑 H_∞제어에 기초하여 PID 제어기를 동조하는 방법으로[7] PID 제어기 파라미터는 식 (7)과 같다.

여기서 는 사용자 정의 파라미터이고,

2.6 Lee 등의 방법

RCGA를 이용하여 PID 제어기를 최적으로 동조하는 방법으로[8] 절대오차적분(IAE), 제곱오차적분(ISE), 시간곱절대오차적분(ITAE) 세 가지 목적함수(성능지수)를 고려하여 PID 제어기 파라미터를 최적으로 동조하는 방법이다.

3. 제약조건을 고려한 RCGA 기반 PID 제어기

기존의 연구[3]-[8]에서 다루어진 PID 제어기 설계 방법은 설계사양으로 표현되는 제약조건이 고려되지 않은 전형적인 비제약성 최적화 문제이다.

따라서 본 논문에서는 제약조건이 존재하는 경우로서 식 (8)과 같은 최대백분율오버슈트(M_p) 및 2% 정착시간(t_s)을 제약사항으로 선정하여 제약성을 갖는 문제로 고려한다.

여기서 c₁과 c₂는 설계자가 제어환경을 고려하여 선정하는 상수이다.

이러한 제약 조건이 수반되면 Lee 외[8]에서 제안한 단순한 RCGA의 최적화 방법은 적용할 수 없게 된다. 이를 해결하기 위한 방법으로 거부전략(rejecting strategy), 복구전략(repairing strategy), 유전 연산자의 보완 전략(modifying genetic operator strategy), 벌점전략(penalizing strategy) 등이 있으며 본 논문에서는 벌점전략[9]을 이용한다.

이는 RCGA가 PID 제어기 파라미터를 찾는 과정에서 집단내의 잠정적인 해들이 제약조건을 위반(부적합한 영역을 탐색)하면 그 위반 정도에 따라 목적함수에 벌점을 추가하도록 하는 방법이다.

벌점함수 P(K)가 결함된 RCGA의 목적함수는 식 (9)와 같이 표현할 수 있다.

F (K) = J (K) + P (K) (9)

여기서 w₁, w₂는 각 제약조건에 대응되는 벌점상수로서 설계자에 의해 도입되는 상수이고, 목적함수 J (K)는 제어환경에 따라 적절히 선택해서 사용할 수 있도록 식 (10)과 같이 절대오차적분(IAE), 제곱오차적분(ISE), 시간곱절대오차적분(ITAE) 세 가지 성능지수를 고려하기로 한다.

여기서 K = [K_p, T_i, T_d]^T∈R³는 PID 제어기 파라미터로 구성되는 벡터이고, e는 설정치와 출력 간의 오차이며, t_f는 이후의 적분값이 무시될 수 있도록 충분히 큰 시간이다.

식 (10)의 목적함수 중에서 ISE는 해석이 용이하여 최적제어기 설계 등에 자주 이용되며, IAE는 오차의 절대 크기를 취함으로써 양이나 음의 오차에 균등한 벌점을 부여하는 효과를 준다. ITAE는 장시간의 과도현상에 대해 벌점을 주는 매우 유용한 기준으로 IAE나 ISE보다 훨씬 더 변별력이 있으며, 이 적분의 최소값은 시스템의 파라미터들이 변하는 경우에 훨씬 더 잘 정의될 수 있다[8].

이렇게 함으로써 제약성 최적화 문제는 식 (9)의 목적함수 F (K)를 최소로 하는 비제약성 최적화 문제로 변환된다.

Figure 2는 지금까지 설명한 과정을 그림으로 나타낸 것이다.

Figure 2

Optimization of a constrained PID control system using the RCGA.

이때 사용되는 RCGA의 제어변수로는 집단의 크기 N= 50, 재생산 계수η= 1.8을 사용하는 구배와 유사한 재생산, 교배확률 Pc= 1.0을 사용하는 수정 단순교배, 돌연변이 확률 Pm= 0.2을 사용한 동적돌연변이를 선택하였다. 동적돌연변이는 진화 초기에는 돌연변이 확률이 크게(Pm= 0.2) 선정되지만 세대가 지날수록 돌연변이 확률이 작아지는 특징이 있어 최적해의 탐색에 유리하다[9].

4. 시뮬레이션

제안한 방법의 유효성을 검증하기 위하여 De Paor와 O'Malley, Venkatashankar와 Chikambaram, Poulin과 Pomerleauuyben, Ho와 Xu 그리고 Wen과 Yingqin, Lee 등의 응답을 서로 비교하는 시뮬레이션을 실시하였다. 시뮬레이션에 사용된 불안정 FOPTD 프로세스는 여러 문헌에서 인용되는 식 (11)의 시스템을 고려하였다.

본 연구에서는 식 (8)에 나타낸 제약조건에서 최대백분율오버슈트가 80% 이하(c1 = 80)로 발생하면서 2% 정착시간이 2.5초 이내(c2 = 2.5)가 되도록 설정하였다. 또한, 식 (9)에서 선정하는 벌점 상수는 경험적으로 w₁ = 10⁵, w₂ = 10⁴으로 선정하였다.

벌점전략을 결합한 RCGA를 통해 탐색된 PID 제어기 파라미터는 Table 1과 같다.

Table 1

PID parameters for the proposed method

비교목적으로 기존의 연구에서 제안한 방법을 사용한 제어성능을 Table 2에 나타내었다. Table 2의 M_p, t_p, t_r 그리고 t_s는 각각 최대 퍼센트 오버슈트, 피크시간, 상승시간, 정착시간을 의미한다. 전체적으로 기존의 연구는 M_p가 크게 발생하고 있는 결과를 보인다.

특히, Venkatashankar와 Chikambaram 방법과 Lee 등이 제시한 방법(ISE)은 M_p가 다른 방법에 비해 작지만 t_s가 상대적으로 길어지는 결과를 보인다.

Table 2

Performances for conventional researches

Figure 3

Control responses by the proposed method

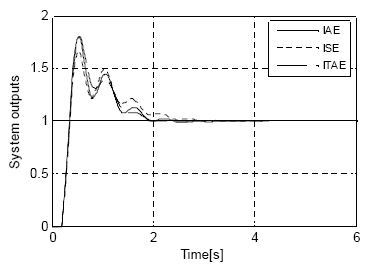
Figure 3은 제안한 방법을 이용해 최적으로 동조한 PID 제어기의 응답을 나타낸 것이고, Table 3은 제어성능을 나타낸 것이다. Figure 3과 Table 3을 통하여 확인할 수 있듯이 제안한 방법은 주어진 제약조건인 M_p ≤ 80 (%) 와 t_s ≤ 2.5(s) 을 완벽하게 만족시키고 있음을 알 수 있다.

Table 3

Performance for the proposed method

5. 결 론

본 논문에서는 복소평면상의 우반부에 극점을 하나 포함하고, 시간지연을 동시에 갖는 시스템인 불안정 FOPTD 프로세스에 대한 PID 제어기 동조 기법을 제안하였다. 특히, M_p 및 t_s의 제약조건이 주어져 제약성 최적화 문제로 주어진 경우를 고려하였으며 벌점전략을 포함한 RCGA를 이용하여 최적으로 PID 제어기를 동조하는 방법을 보였다. 이를 위해 RCGA의 목적함수에 벌점함수를 결합한 전략을 사용하였으며 세 가지 성능지수인 IAE, ISE 그리고 ITAE를 최소로 하는 관점에서 최적으로 PID 제어기를 동조하였다.

제시한 기법을 예제 프로세스에 적용하여 시뮬레이션을 수행한 결과 주어진 제약조건을 완벽하게 충족시키는 결과를 확인할 수 있었다.

Acknowledgments

본 연구는 2012년도 대외경쟁력 강화를 위한 연구 강화지원사업의 지원으로 수행한 연구결과입니다.

References

D. E. Kim, and G. G. Jin, “Model-based tuning rules of the PID controller using real-coded genetic algorithms”, Journal of Institute of Control, Robotics and Systems, 8(12), p1056-1060, (2002), (in Korean). [https://doi.org/10.5302/J.ICROS.2002.8.12.1056]
M. Zhuang, and D. P. Atherton, “Automatic tuning of optimum PID controllers”, Control Theory and Applications, IEE Proceedings D, 140(3), p216-224, (1993). [https://doi.org/10.1049/ip-d.1993.0030]
A. M. De Paor, and M. O'Malley, “Controllers of ziegler-nichols type for unstable process with time delay”, International Journal of Control, 49(4), p1273-1284, (1989).
V. Venkatashankar, and M. Chidambaram, “Design of P and PI controllers for unstable first-order plus dead time delay systems”, International Journal of Control, 60(1), p137-144, (1994). [https://doi.org/10.1080/00207179408921455]
E. Poulin, and A. Pomerleau, “PID tuning for integrating and unstable processes”, Control Theory and Applications, IEE Proceedings, 143(5), p429-439, (1996). [https://doi.org/10.1049/ip-cta:19960442]
W. K. Ho, and W. Xu, “PID tuning for unstable process based on gain and phase margin specifications”, Control Theory and Applications, IEE Proceedings, 145(5), p392-396, (1998). [https://doi.org/10.1016/0005-1098(94)00130-B]
T. Wen, Y. Yingqin, and N. Yuguang, “Tuning of PID controller for unstable process”, Proceedings of the 1999 IEEE International Conference on Control Applications, 1, p121-124, (1999). [https://doi.org/10.1109/CCA.1999.806155]
S. L. Lee, Y. H. Lee, J. K. Ahn, J. K. Son, K. T. Ryu, and M. O. So, “PID Control of unstable processes with time delay”, Journal of the Korean Society of Marine Engineering, 33(5), p721-728, (2009), (in Korean). [https://doi.org/10.5916/jkosme.2009.33.5.721]
G. G. Jin, Genetic Algorithm and Their Application, Gyowoosa, (2002), (in Korean).