영역확장법 및 로그격자를 이용한 수치모델링 효율 향상 연구
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
유한차분법에 바탕을 둔 수치모델링은 컴퓨터기술의 발전과 함께 다양하게 이용되고 있다. 하지만 대용량의 컴퓨팅 리소스를 필요로 하는 문제를 지니고 있다. 이러한 한계를 극복하기 위해 본 연구에서는 로그격자와 영역확장법을 함께 적용하여 수치모델링 알고리즘을 제안하였다. 기존의 일반적인 등격자 유한차분법과 비교를 통해 알고리즘의 타당성 및 정확성을 검증하였으며, 수치예제를 통해 새롭게 제시된 알고리즘의 계산 효율성을 확인하였다.
Abstract
Numerical modeling based on the finite difference method has been widely used with improved computer technology. However, high-capacity computing resources are required for this technique. To overcome this limitation, we propose an algorithm the employs a logarithmic grid in conjunction with the expanding domain method. The proposed algorithm was verified through comparison with numerical results obtained with a conventional method. The results confirmed that our algorithm can improve computational efficiency.
Keywords:
Numerical modeling, Finite difference method, Logarithmic grid, Expanding domain method키워드:
수치모델링, 유한차분법, 로그격자, 영역확장법1. 서 론
탄성파탐사는 해저 유·가스자원 개발 목적의 탐사에서 가장 보편적으로 이용되는 물리탐사기술로, 지하구조에 따른 다양한 파동전파 현상의 분석을 통해 지하매질을 영상화할 수 있다[1][2]. 지하구조 내부에서 음향 임피던스(a-coustic impedance) 차이에 의해 반사 또는 굴절 등 다양한 특성의 탄성파 거동이 기록되며, 이를 정확히 모사할수록 고해상도의 지하구조 규명이 가능하다. 파동의 특성모사를 위한 계산도구로서 주로 사용되는 수치모델링은 파동방정식을 이용하여 탄성파의 물리적 현상을 예측하는 방법으로, 파동전파에 대한 이해뿐만 아니라 인공 탄성파탐사의 설계 및 자료해석 등에도 활용된다[3]-[5].
수치모델링에서 탄성파 파동방정식을 해결하기 위한 방법에는 유한차분법(FDM), 유한요소법(FEM), 경계요소법(BEM) 등 다양한 방법들이 있다. 그 중 널리 이용되는 유한차분법은 알고리즘의 구현이 간단하고 비교적 복잡한 모델에 대해서도 정확한 거동의 모사가 가능하다. 또한 한 번의 모델링 수행을 통해 다양한 정보를 취득할 수 있는 장점이 있다[5]. 유한차분법의 정확도와 안정성의 향상을 위하여 불규칙 격자법(Irregular grid), 엇갈린 격자법(Staggered grid), 회전된 엇갈린 격자법(Rotated staggered grid) 외에 고차원의 연산자를 이용하는 등 다양한 방법들이 제시되었다[6]-[8].
하지만 이와 같은 방법들은 여전히 대용량의 리소스와 긴 계산시간을 필요로 하는 연산효율 측면의 문제를 지니고 있다. 이러한 문제점을 극복하고자 W. Ha and C. Shin. [9]은 연산량의 감소와 동시에 인공적인 경계에 의한 영향을 제거할 수 있는 방법으로 라플라스 영역에서 깊이방향으로 로그격자(logarithmic grid)를 적용하였으며, Choi et al. [10]은 주파수영역에서 로그격자를 적용하였다. S. Suh and B. Wang. [11]과 Ryu et al. [12]은 영역확장법(expanding do-main method)을 제시하여 계산시간 및 연산량의 효율에서 좋은 결과를 보여주었다. 한계유전을 비롯한 극한 지역 또는 대수심 탐사 등 고난도∙대규모 환경에 대한 탐사로서 3차원 탄성파 탐사가 수행되는 최근 추세에서, 대용량의 탐사자료를 처리하기 위해 고가의 소프트웨어 시스템과 고성능의 컴퓨터를 사용하거나 용역기관에 의존하고 있다[13]. 이에 따라 높은 연산효율을 갖는 알고리즘은 이러한 한계성을 극복할 수 있을 뿐만 아니라 비교적 사양이 낮은 개인용 컴퓨터(PC)에서의 자료처리를 가능하게 할 수 있다.
본 논문에서는 연산량의 감소를 통한 수치모델링의 효율을 향상시키고자, 로그격자 및 영역확장법을 적용한 알고리즘을 개발하였으며 여러 가지 수치예제를 통해 새롭게 개발된 알고리즘에 대한 정확성 및 효율성을 검증해 보았다.
2. 이 론
2.1 유한차분법
균질, 등방성매질에서의 3차원 음향 파동방정식은 식 (1)과 같이 편미분방정식의 형태로 표현할 수 있다.
| (1) |
여기서 ∇2는 라플라시안 연산자, c는 매질의 속도, u는 파동장, t는 시간의 변수를 나타낸다. f는 음원의 파형, δ는 델타함수이며, x0, y0, z0는 음원의 위치를 나타낸다.
유한차분법은 테일러급수 전개식을 통해 미분형태의 지배방정식을 차분방정식으로 근사시켜 수치해석 하는 방법으로, 차분 시 사용하는 함수에 따라 전향차분, 후향차분, 중앙차분으로 나눌 수 있다. 식 (1)의 음향 파동방정식을 1차원으로 가정하고 시간 및 공간의 변화에 대한 미분 연산자를 유한차분법을 통해 근사하면 식 (2)와 같이 표현할 수 있다. 이때 ∆t, ∆x는 각각 시간과 공간에서의 격자간격을 나타낸다.
| (2) |
유한차분법을 통해 근사한 파동방정식을 이용하여 모델링을 수행하기 위해서는 대상이 되는 모델을 격자구조로 표현해야 한다. 이때 일정 수준의 정확도를 유지할 수 있는 격자간격을 설정하기 위해 안정조건 및 분산분석을 수행한다[14]. 분산분석을 위한 최소파장 λmin의 길이는 식 (3)으로부터 구할 수 있다. 여기서 υmin은 매질의 최저속도이며, fmax는 음원의 최대주파수이다. 이후 모델링 수행 시 고려되는 최소파장을 일정수준의 정확도를 유지시켜주는 최소 격자수 G로 나눠줌으로써 격자간격 ∆grid를 구할 수 있다.
| (3) |
| (4) |
식 (3)과 식 (4)에 따라 음원의 최대주파수가 증가할수록 최소파장의 길이가 짧아지면서 일정한 수준의 정확도를 유지하기 위해서는 격자간격이 조밀해진다. 이로 인해 동일한 크기의 모델을 표현하기 위한 총 격자의 개수가 증가하며, 수치모델링에서 격자개수의 증가는 고차원으로 갈수록 연산량 및 연산시간을 기하급수적으로 증가시킨다.
2.2 로그격자를 이용한 모델링
W. Ha and C. Shin. [9]을 통해 제안된 로그격자를 이용한 수치모델링 방법에서는 파동이 공간에 대한 변수 x로 이루어진 새로운 함수 X = f(x)를 따라 전파된다고 가정하였을 때, 1차원 음향파동방정식을 식 (5)와 같이 재 정의하였다.
| (5) |
새로운 함수 X는 자연로그 함수로서 식 (6)과 같이 정의한다.
| (6) |
동일한 방법으로 공간에 대한 변수 y, z에 대해서 각각 새로운 자연로그 함수 Y, Z를 정의할 수 있다. 이때 모델의 상부를 수면으로 가정할 경우, z축에 대해서는 양의 증가만 고려하여 새로운 함수 Z는 식 (7)과 같다.
| (7) |
Figure 1과 같이 등격자와 로그격자를 비교하였을 때, 로그격자는 원점에 가까울수록 등격자에 비해 격자간격이 더욱 조밀하여 보다 정밀한 표현이 가능하다. 하지만 원점에서 멀어질수록 격자 한 개가 나타내는 크기가 대수적으로 증가하여 정확도가 감소하게 된다. 이와 같은 이유로 로그격자를 이용할 경우, 대상이 되는 모델의 특정 부분을 격자의 중심에 위치시킴으로써 더욱 정확하게 묘사할 수 있다.
또한 등격자와 동일한 격자수를 이용하였을 때 보다 넓은 영역을 표현할 수 있어 대규모의 지역에 대한 개략적인 모델링을 등격자 보다 적은 격자수를 이용하여 빠르게 수행할 수 있고, 같은 시간동안 파동이 인공적인 경계에 도달하지 않아 경계에 의한 반사파의 영향을 무시할 수 있다.
2.3 영역확장법
파동은 음원이 발생하는 지점부터 매질을 통해 주변으로 전파되며, 이때 초기시간에는 음원 발생지점의 인근주변을 제외하면 파동장의 변화가 ‘0(zero)’이다. 영역확장법은 이러한 사전에 예측 가능한 파동장의 변화가 없는 영역의 연산을 생략함으로써 계산비용을 줄일 수 있는 방법이다. 영역확장법의 연산방법에는 (1) 등속도 방법, (2) 아이코널 방정식 풀이법, 그리고 (3) 진폭 비교방법이 있다. 등속도 방법은 속도변화를 고려하지 않고, 최대속도에 대한 주시를 통해 파동장의 확장속도를 구하는 방법으로 간단한 계산에 비해 다양한 속도변화를 갖는 모델에서는 비효율적이다. 아이코널 방정식 풀이법은 다른 두 가지 방법에 비해 정확성은 높지만, 아이코널 방정식의 계산 자체만으로도 연산량이 많아 효율성 향상에는 부적합하다. 진폭비교 방법은 영역의 경계를 설정하고 경계인근에 나타나는 파동장의 변화에 따른 진폭값의 가감을 파악하여 계산영역을 확장하는 것으로, 계산이 매우 간단하며 적용이 간편하다[11][12].
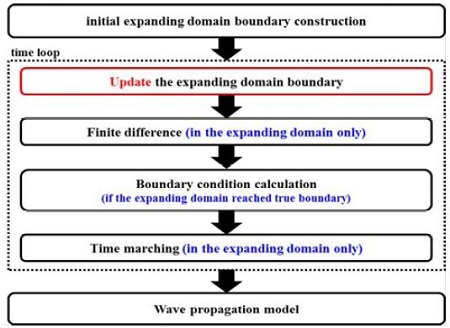
Figure 2는 Ryu et al. [11]에서 제시한 영역확장법을 이용한 수치 모델링 알고리즘의 흐름도이다. 일반적인 시간영역에서의 수치모델링 과정에서 매 시간간격마다 연산영역에서의 진폭변화를 감지하여 확장여부를 판단하고, 모든 계산은 영역 내에서만 수행한다. 특히 경계조건은 연산영역의 경계가 초기에 주어진 실제 모델의 경계와 맞닿았을 때만 계산함으로써 기존 방법과 비교하여 경계조건에 대한 연산횟수가 매우 감소된다. 시간전진(time marching) 기법 또한 연산영역 내에서만 수행된다.
3. 수치모형실험 및 결과
본 연구에서는 효율성 향상을 위하여 로그격자 및 영역확장법을 적용한 알고리즘을 개발하였으며, 수치예제를 통해 알고리즘의 정확성 및 효율성을 검증하고자 하였다. 영역확장법은 진폭 비교방법을 적용하였으며, 격자개수 및 CPU 계산시간을 통해 연산효율을 비교하였다.
3.1 로그격자 알고리즘 검증
영역확장법 적용에 앞서 로그격자 알고리즘의 타당성 및 정확성 검증을 위해 기존의 일반적인 등격자 유한차분법의 수치모델링 결과와 비교하였다. 1.5km/s의 균질한 속도를 갖는 수층을 대상으로 동일한 지점에 음원과 수진기를 위치시켜 신호의 정확성을 비교하였다.
Figure 3은 등격자에서의 일반적인 유한차분법과 로그격자를 이용한 수치모델링 결과이다. Figure 3 (c)의 정규화결과에서 파형 및 진폭이 일치함을 확인할 수 있었으며, 이를 통해 로그격자 알고리즘의 타당성 및 정확성을 확인하였다. Table 1은 등격자 및 로그격자를 사용하였을 때, 200×200×100의 모델을 나타내기 위해 필요한 격자수와 메모리 용량을 나타낸 것이다. x, y축은 모델의 중심을 원점으로 하여 양방향(+x, -x, +y, -y)으로 로그격자를 적용하였으나, z축은 깊이 방향의 단방향(+z)에 대해서만 적용함으로써 z축에 대한 격자수의 감소폭이 더욱 큰 것을 확인하였다. real 32bit 기준 로그격자가 등격자 대비 40.17% 정도의 메모리를 사용하는 것을 통해 메모리 사용 효율이 향상되었음을 확인하였다.
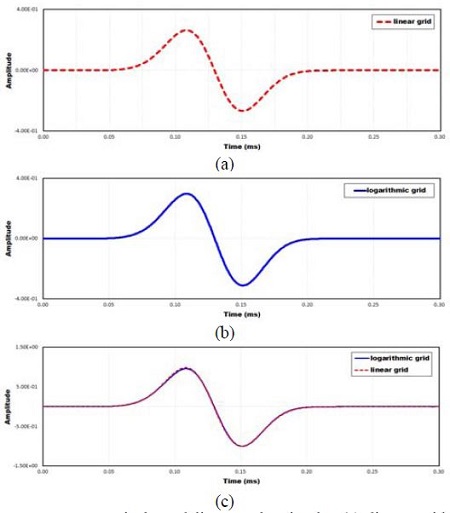
Numerical modeling results: in the (a) linear grid, (b) logarithmic grid, and (c) normalization result
3.2 영역확장법 적용
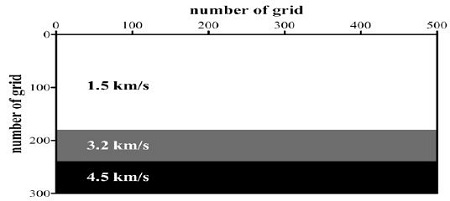
로그격자 알고리즘에 영역확장법을 적용하여 연산영역 경계의 확장을 확인하고, 연산시간 효율을 비교하였다. 실험에는 Figure 4와 같이 수평 3층 구조의 평면을 갖는 3차원 모델을 사용하였으며, 3차원의 속도모델을 2차원의 xy평면으로 나타낸 것이다. 속도모델의 최상부층에 1.5km/s의 속도를 갖는 수층이 존재하며, 각각 3.2km/s, 4.5km/s의 속도를 갖는 수평층으로 구성되어 있다. 속도변화에 따른 영역확장법의 확장속도를 고려하기 위해 균질매질이 아닌 수평 3층 구조를 사용하였다.
모델링 변수는 Table 2와 같다. x축, y축 및 z축 격자간격은 2m로 동일하며, 시간간격 0.1ms, 총 기록시간은 0.3초이다. 음원은 절단주파수 200Hz의 1차 미분 가우스 함수(first derivative gaussian function)를 사용하였다.
영역확장법은 연산영역 경계의 2격자 내부에서 최대 진폭 크기 1% 이상의 진폭변화가 나타날 경우 영역을 확장하도록 하였으며, 확장폭은 10격자로 설정하였다. 초기 연산영역의 경계는 음원의 위치로부터 좌∙우∙하부에 각 10격자 떨어진 지점으로 설정하였다.
Figure 5는 알고리즘의 로그격자 변환과정을 통해 취득한 로그격자에서의 속도모델을 Figure 4와 동일한 위치에서 2D로 나타낸 것이다. 로그격자로 변환됨에 따라 속도모델의 표현이 달라지는 것을 확인하기 위해 축을 격자의 개수로서 표시하였다. Figure 4와 비교하였을 때, 수평 3층 모두 등격자일 때보다 적은 격자수로 표현되며 대수적으로 증가하는 로그격자로 인해 깊이방향으로 증가할 수록 수평층의 두께가 얇게 표현되는 것을 확인할 수 있다.
로그격자 적용에 따른 계산량의 감소는 500×500×300에서 405×405×203으로 real 32bit 기준 0.28GB에서 0.12GB로 기존대비 42.85% 수준으로 감소하였다.
Figure 6은 제안알고리즘을 이용하였을 때 시간변화에 따른 파동장 계산영역의 변화를 파선으로 나타낸 것이다. 0.09초(Figure 6 (a))에서 0.15초(Figure 6 (b))의 결과를 살펴보면 모델 상부의 수면을 맞고 되돌아온 반사파의 영향으로 수평방향 확장속도가 더욱 빨라졌음을 확인할 수 있으며, 0.15초(Figure 6 (b))에서 0.21초(Figure 6 (c))의 결과를 통해 속도변화가 나타나는 구조에 의해 수평 및 수직방향의 확장속도가 달라짐을 확인할 수 있다. 또한 로그격자를 적용함으로써 격자 간격이 증가함에 따라 구형발산하는 파동의 형태가 시각적으로 왜곡되어 나타나는 것을 확인할 수 있다.
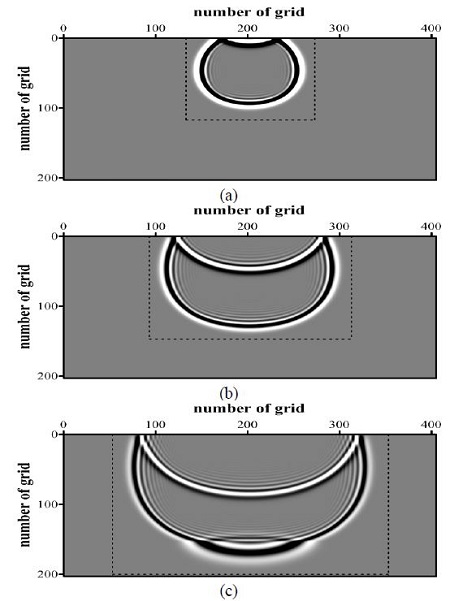
Snapshots of wavefield in logarithmic grid with expanding boundary: (a) 0.09s, (b) 0.15s, and (c) 0.21s
로그격자 유한차분법 알고리즘에 영역확장법을 적용하였을 때 CPU 계산시간은 26.8분으로, 적용하지 않았을 때의 100.1분과 비교하여 약 26% 수준으로 연산시간이 감소되었음을 확인하였다(CPU 제원 : 6 core Intel Xeon E5-2640 [2.5GHz, 15MB L3, 72GT/sec QPI]). 등격자와 비교하여 로그격자를 적용할 경우 격자의 개수는 42.85% 수준으로 감소하였으며, 이에 영역확장법을 적용함으로써 초기시간에서의 연산영역 범위를 줄여 계산시간을 26% 수준으로 감소시킬 수 있었다.
4. 결 론
본 논문에서는 수치모델링의 연산효율을 향상시키고자 로그격자 및 영역확장법을 이용한 유한차분법 기반의 알고리즘을 제안하였다.
로그격자 알고리즘의 정확성을 검증하기 위하여 기존의 등격자 유한차분법을 이용한 수치모델링 결과와 비교를 수행하였으며, 트레이스 비교 결과에서 합리적인 결과를 확인하였다. 리소스 효율을 위한 비교에서는 200×200×100 크기의 모델을 표현하기 위해 등격자 대비 40% 수준의 메모리를 사용함을 확인하였다. 정확성 및 효율성이 검증된 로그격자 알고리즘에 영역확장법을 적용하고, 수평 3층 구조의 속도모델을 이용한 수치예제에서는 메모리 사용량은 42.85% 수준으로 감소, 계산시간은 26% 수준으로 단축됨을 확인하였다.
본 논문에서 수행한 수치예제의 경우, 로그격자와 영역확장법의 결합으로 기존의 등격자 유한차분법 대비 메모리 사용량과 계산시간이 절반 수준으로 감소하였으며, 이를 통해 본 논문에서 제안한 알고리즘을 이용하여 계산효율이 향상될 수 있음을 확인하였다. 이와 같은 메모리 사용의 효율성 및 계산시간의 감소는 대상모델의 차원 및 크기가 커질수록 극대화될 것으로 판단되며, 특히 고성능 슈퍼컴퓨터에 비해 CPU 및 메모리 성능이 부족한 저성능 개인용 컴퓨터에서의 연산효율을 높일 수 있을 것으로 생각된다.
최근 컴퓨터 기술의 비약적인 발전과 함께 유한차분법을 이용한 수치모델링의 응용분야가 다양해지고 있으며 효율적인 알고리즘의 필요성이 증가하고 있다. 본 연구에서 제안하는 알고리즘은 이러한 필요성에 맞춰 탄성파 파동모사 뿐만 아니라 수중음향 환경과 같이 고주파수대역을 사용하는 경우에도 적용 가능할 것으로 기대된다.
Acknowledgments
본 연구는 국방과학연구소[수중복합음향환경 모델링 및 고속 수중운동체 탐지/식별 기법 연구(UD150002DD)]의 지원으로 수행되었으며, 교육과학기술부의 재원으로 한국연구재단의 지원을 받아 수행된 산학협력 선도대학(LINC) 육성사업의 연구결과입니다.
References
- S. Kim, J. Kim, and H. Kim, “A study on characteristics of marine geological structure by numerical modeling of seismic waves”, Proceedings of Korean Society of Marine Engineers Conference, p122, (2011).
- C. S. Cho, and H. I. Lee, “Application of convolutional perfectly matched layer method to numerical elastic modeling using rotated staggered grid”, Jigu-Mulli-wa-Mulli-Tamsa, 12(2), p183-191, (2009).
-
J. T. Etgen, and M. J. O’Brien, “Computational methods for large-scale 3D acoustic finite-difference modeling: A tutorial”, Geophysics, 72, p SM223-SM230, (2007).
[https://doi.org/10.1190/1.2753753]

-
C. Ramsden, G. Bennett, and A. Long, “High-resolution 3D seismic imaging in practice: analysis”, The Leading Edge, 24(4), p423-428, (2005).
[https://doi.org/10.1190/1.1901397]

-
C. Cho, and M. Son, “Application of ADE-PML boundary condition to SEM using variational formulation of velocity-stress 3D wave equation”, Jigu-Mulli-wa-Mulli-Tamsa, 15(2), p57-65, (2012).
[https://doi.org/10.7582/gge.2012.15.2.057]

- Y. Liu, and M. K. Sen, “Advanced finite-difference methods for seismic modeling”, Geohorizons, 14(2), p5-15, (2009).
- Y. Liu, and M. K. Sen, “Advanced finite-difference methods for seismic modeling”, Geohorizons, 14(2), p5-16, (2009).
-
M. Kindelan, A. Kamel, and P. Sguazzero, “On the construction and efficiency of staggered numerical differentiator for the wave equation”, Geophysics, 55, p107-110, (1990).
[https://doi.org/10.1190/1.1442763]

-
W. Ha, and C. Shin, “Efficient laplace-domain modeling and inversion using an axis transformation technique”, Geophysics, 77, pR141-R148, (2012).
[https://doi.org/10.1190/geo2011-0424.1]

- S. Choi, D. J. Min, W. Oh, W. Chung, W. Ha, and C. Shin, “Frequency-domain acoustic and elastic modeling and waveform inversion in the logarithmic grid set”, Journal of Seismic Exploration, 23, p103-130, (2014).
-
S. Suh, and B. Wang, “Expanding domain methods in GPU based TTI reverse time migration”, SEG Technical Program Expanded Abstracts, p3460-3464, (2011).
[https://doi.org/10.1190/1.3627917]

-
D. H. Ryu, A. Kim, and W. S. Ha, “Expanding domain method for 3D time-Laplace-domain hybrid modeling”, Geosystem Engineering, 18(5), p1-7, (2015).
[https://doi.org/10.1080/12269328.2015.1047966]

- J. Ji, and Y. G. Choi, “3D Seismic data processing methodology using public domain software system”, Jigu-Mulli-wa-Mulli-Tamsa, 13(2), p159-168, (2010).
- S. H. Jang, C. S. Shin, K. J. Yoon, S. Y. Suh, and S. R. Shin, “A dispersion analysis for minimum grids in the frequency domain acoustic wave equation”, Jigu-Mulli-wa-Mulli-Tamsa, 3(2), p39-47, (2000).