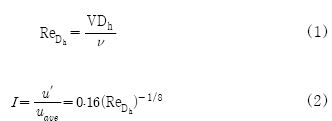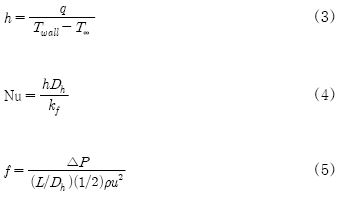Numerical analysis on heat transfer and pressure drop characteristics in a horizontal channel with various ribs
Turbulent flow and heat transfer in a channel with a detached rib array have been simulated. The computations are based on the finite volume method with the SIMPLE algorithm. The forms of ribs considered in this study were rib with rectangular cross section, rib with groove, broken rib, and V-shaped rib. The ribs were deployed transverse or aligned 60o to the main direction of the flow. Local heat transfer coefficients were obtained at various Reynolds numbers within the turbulent flow regime. Area-averaged data were calculated in order to compare the overall performance of the tested ribbed surfaces and to evaluate the degree of heat transfer enhancement induced by the ribs with respect to the smooth channel. The highest heat transfer occurred for the rib with groove which was aligned 60o to the main flow direction. Performance factor was decreased with the increase of velocity, and it was found that the best performance factor was obtained in the low velocity region.
초록
열전달 향상을 위하여 이차유동을 발생시켜 열전달을 증가시키는 방법에는 여러 가지가 있다. 본 연구에서는 수평채널에 다양한 형태의 립을 설치하여 유속을 변화시켰을 때의 열전달 및 압력강하 특성을 수치해석을 통하여 고찰하였다. 립은 수평채널의 아랫면에 설치하였고, 립의 높이는 5mm이다. 립이 60o 기울어지고 그루브도 설치된 경우 열전달 특성이 가장 우수하게 나타났는데, 이는 주유동이 립을 따라 흘러가면서도 유속이 어느 정도 유지되기 때문이다. 끊어진 립에서 주유동이 립의 저항을 적게 받으면서 압력강하가 가장 작게 나타났다. 모든 립의 형태에서 유속이 증가함에 따라 열전달이 향상되는 경향을 보였지만 성능계수는 감소하였다.
Keywords:
Rib, Heat transfer characteristics, Friction factor, Performance factor, Pumping power, 립, 열전달 특성, 마찰인자, 성능계수, 펌핑동력1. 서 론
유동장 내에서의 주기적인 유동간섭은 일반적으로 난류발생을 촉진시켜 열전달을 증진시킨다. 이러한 현상을 이용하여 열교환기, 가스냉각식 장치, 전자부품 냉각장치 및 터빈 블레이드의 내부 냉각 등에서 열전달 효율을 높이기 위해 주기적인 유동 장애물을 열전달 면에 부착하고 있다. 이차유동을 통해 열전달을 증진시키는 방법 중에는 립(rib), 핀(fin), 딤플(dimple), 델타 윙(delta wing)등이 사용된다.
이중 립은 단면적이 크기 때문에 열전달효과가 뛰어나므로 많은 연구가 수행되어 왔다.
Tanda[1]에서는 끊어진 립(broken rib)이 V-형태의 립보다 열전달 향상이 크다는 것을 실험적으로 연구하였다. Aharwal 외[2]에서는 립에 각도를 주어서 립 주위의 난류유동에 대해서 연구하였다. 그리고 Karwa 외[3]에서는 립에 챔버 각을 주어 열전달특성을 연구하였다. 기존 연구에서는 실험을 통하여 열전달 특성과 압력강하에 대해서 분석하였으나, 실험적인 오차가 존재하고 여러 가지 변수가 있기 때문에 다양한 경우에 대하여 실험을 진행하기 위해서는 많은 시간 및 자원이 투입이 필요하다. 본 연구에서는 열/유체 수치해석 상용프로그램인 FLUENT[4]를 이용하여 기존의 실험[1]에서 밝혀진 특성을 수치해석을 통하여 검증하였다. 또한, 다양한 형태의 립을 사각채널에 설치하여 열전달 및 압력강하 특성을 연구하였다.
2. 수치해석
2.1 수치해석 방법 및 경계조건
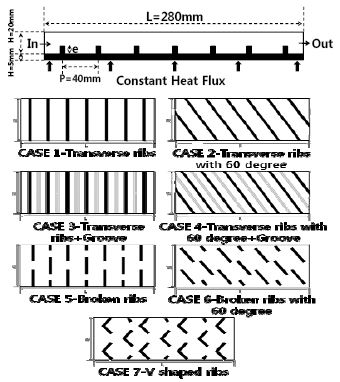
Figure 1은 해석 대상의 개략도와 립의 형상을 나타낸 것이며, 채널 높이(H)가 20mm이고 수력직경이 33.3mm인 사각채널을 이용하였다. 립의 높이/채널 높이(e/H)를 0.25로 고정하고 해석을 수행하였다. 아래 면에서 일정한 열 유속 1800W/m2이 주어지고, 입구에서는 300K의 공기가 유입된다.
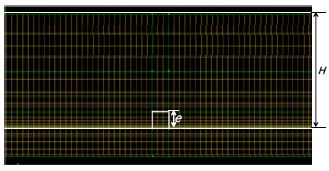
난류 모델로는 k-ε standard 모델을 사용하였으며, 이 모델은 경계층에서의 해석이 순조롭게 이루어지기 위해서 벽면근처에 격자를 조밀하게 배치해야 한다[5]. 일반적으로 k-ε standard 모델을 사용하기 위해서는 벽면에서 첫 번째 격자까지의 y+값이 10∼100 사이 값이어야 한다. 본 수치해석에서 y+값이 32이므로 k-ε standard 모델을 사용하기에 타당하다. Figure 2에 격자계를 나타내었는데, 모든 격자를 사각 형태로 생성하였으며, 격자수는 수치해석을 통해 격자를 5만개씩 증가시키며 온도 및 압력의 수렴성을 테스트 하였다. 수치해석 결과 격자수가 약 140만개에서 온도 및 압력 값이 수렴 하였는데, 140만개 이상에서 값의 차이가 거의 없었기 때문에 최적화 된 약 140만개로 결정하였다. 사각채널의 경우 입구와 출구를 제외한 모든 면이 벽으로 된 채널로 가정하였으며 난류강도는 Reynolds 수의 변화에 따라 정의했다. Table 1은 유속에 따른 Reynolds 수와 난류강도의 값으로 다음과 같이 정의된다[6]. 여기서 I는 난류강도를 나타내며, uaue는 x방향의 평균속도를 나타낸다.
2.2 Nusselt 수 및 마찰인자
표면에서 열전도에 의해 전달된 열에너지는 대류에 의해 자유유동에 전달된 열에너지와 평형을 이루어야 하며, 이 때 열전달계수는 Newton의 냉각법칙에 의해 계산된다. 열전달계수와 Nusselt 수 및 마찰인자(friction factor)는 다음과 같다. 여기서 h는 열전달계수이며, Twall는 벽면 온도, T∞는 유체 온도를 나타낸다.
2.3 성능계수(Performance Factor; PF)
열전달 성능이 향상되더라도 압력손실이 증가하면 그 만큼 펌핑 동력이 많이 소요되므로 압력손실에 대한 열전달의 비를 계산하여 이 값이 커졌는가를 확인하는 작업이 필요하다. 일정한송풍력에서 압력손실에 대한 열전달 비를 나타내는 성능계수는 다음과 같이 정의하였다[7]. 여기서 Nu0 및 f0는 매끈한 사각채널에서의 값을 나타낸다.
2.4 펌핑동력(Pumping Power)
동일한 펌핑동력에서의 열전달 향상 능력을 비교하기 위해서 Bergles 외[8]에서는 다음과 같은 식을 제안하였다.
Nu0 = 0.023Re00.8Pr0.4 (7)
여기서 Re0는 립이 설치된 사각채널에서의 Reynolds 수와 마찰인자를 함께 고려한 값으로써 다음과 같다.
Re0 = (21.74fRe3Dh)0.357 (8)
3. 결과 및 고찰
3.1 열전달 특성
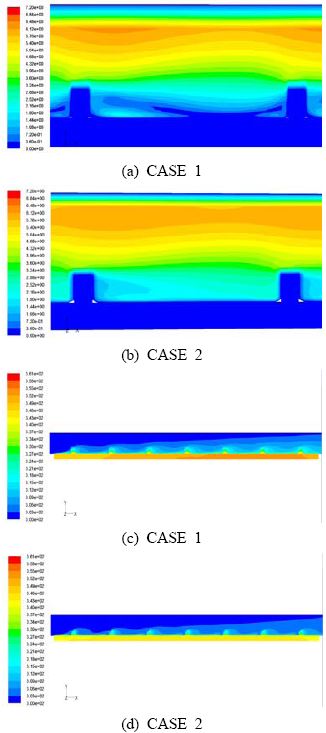
수치해석의 타당성을 입증하기 위하여 Tanda의 실험장치와 동일한 조건을 도입하여 해석하였다. 수치해석 방법 및 경계조건(2.1절)에서 명시한 조건이 Tanda의 실험과 동일한 조건이며 Figure 1에서 CASE 1이 Tanda의 실험에 사용되었던 형상과 동일한 형상이다. 속도장과 온도장을 Figure 3에 나타내었다. 모든 형상에서 립과 립 사이에서 발생하는 유동의 박리와 재부착이 현저하게 나타났으며, 이는 매끈한 덕트에 비하여 열전달이 향상되는 주요한 이유 중의 하나이다. 끊어진 립에서 2차유동이 가장 활발히 일어나면서 열전달이 활발해진다. 이는 Figure 3을 보면 알 수 있듯이 끊어진 립이 난류가 크게 발생하면서 다른 형상보다 벽면을 냉각하는 영역이 넓게 나타났기 때문이다. CASE 1의 경우 다른 형상보다 유동이 원활하지 못하고 벽면 인접한 부분(y/H=0.05)의 유속이 작아지면서 다른 형상에 비해 평균 Nusselt 수가 작은 것을 알 수 있다.
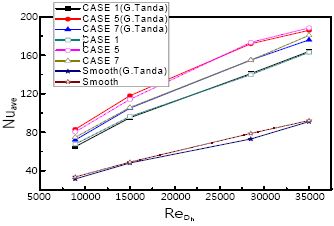
Figure 4는 Tanda의 실험과 수치해석 결과 값을 비교한 것이다. 립이 설치되었을 때 매끈한 덕트와 열전달 특성을 비교하기 위하여 매끈한 덕트에 대하여 Nusselt 수를 구하였다. 매끈한 덕트와 CASE 1, CASE 3, CASE 7의 비교 결과 실험과 수치해석의 오차는 약 0.5%로 계산 되었다. 레이놀즈수에 따른 평균 Nusselt 수를 Tanda의 실험결과와 비교한 결과 정확하게 예측하고 있음을 알 수 있다.
3.2 Nusselt 수 및 마찰인자
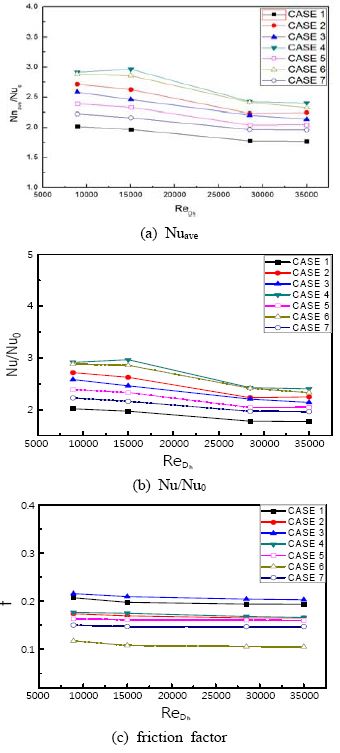
Figure 5 (a)는 유속의 변화에 따른 Nusselt 수의 분포를 나타낸다. Reynolds 수가 증가하면서 모든 형상의 립에 대해서 열전달 효과가 좋아지는 것을 알 수 있다.
Figure 5 (b)는 립이 설치된 경우의 평균 Nusselt 수를 매끈한 채널에서의 평균 Nusselt 수로 무차원화한 무차원 평균 Nusselt 수 분포를 Reynolds 수의 변화에 따라 나타낸 그래프이다. 유속이 증가할수록 무차원 평균 Nusselt 수는 감소하는 경향을 보인다. 이것은 매끈한 채널에 비하여 립이 설치된 채널에서 열교환량의 증가비율이 유속이 증가함에 따라 적어지기 때문이다. 각도 60o인 립과 그루브가 함께 있는 경우인 CASE 4에서 가장 높은 열전달 계수가 나타났으며, 매끈한 채널에 비해 최대 3배 정도 열전달이 향상되었다.
Figure 5 (c)는 유속에 따른 마찰인자를 나타낸 것이다. 각도가 60o 인 CASE 2가 90o 인 CASE 1 보다 낮은 마찰인자를 나타냈고, 이것은 60o 일 때 주유동이 립을 따라서 원활하게 흘러가기 때문에 90o에 비해서 상대적으로 낮은 압력손실을 유발하기 때문이다. 유속의 증가량에 비해서 압력강하의 증가비율이 작아지면서 유속의 증가에 따라 마찰 인자가 감소하는 경향을 나타냈다.
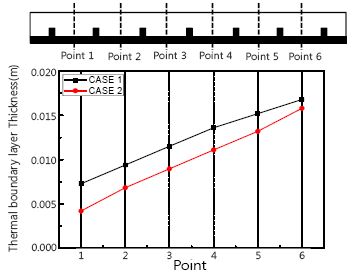
Figure 6을 보면 알 수 있듯이 CASE 1 보다 CASE 2가 벽면에 가까운 곳(y/H=0.05)에서의 유속이 크다. 또한, 열 경계층의 두께가 CASE 2가 CASE 1보다 얇다는 것을 Figure 7에서 확인할 수 있다. 이는 립의 각도가 90o 일 때 주유동이 립에 강하게 부딪히면서 유속이 매우 느려지는 반면에 립의 각도가 60o 일 때 주유동이 립을 따라 타고 흘러가면서 유속이 급격히 작아지지 않기 때문이다. 따라서 주유동이 벽면에 영향을 미치며 다른 경우도 그루브가 삽입된 립이 높은 Nusselt 수를 나타낸다. 이것은 립에 의해서 발생되는 이차유동뿐만 아니라 그루브에 의해서 유동의 교란이 더 활발히 일어나기 때문이다.
3.3 성능계수
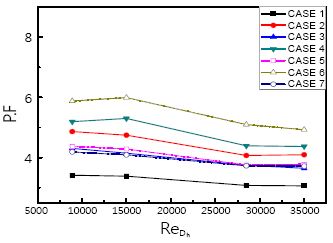
Figure 8은 유속의 변화에 따른 압력손실과 열전달향상을 동시에 고려한 성능계수를 나타낸다. CASE 7에서 가장 높은 성능계수를 나타내었으며, 평균 열전달계수가 가장 높았던 CASE 4보다 성능계수가 높은 이유는 끊어진 립에서 유동저항을 많이 받지 않으며 압력손실이 낮았기 때문이다. 즉, 끊어진 립에서 열전달 향상에 비해 압력강하가 작게 일어남을 보인다. 대부분의 경우 가장 낮은 유속 조건에서 가장 높은 성능계수 값을 보였으며 유속의 증가에 따라 감소하는 경향을 보인다. 이것은 모든 CASE에 대하여 높은 유속보다는 낮은 유속에서 적용하는 것이 효과적이라는 것을 보여준다.
3.4 펌핑동력
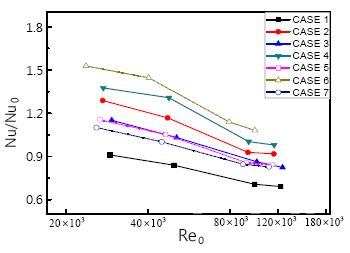
Figure 9는 펌핑동력에 따른 무차원 평균 Nusselt 수를 나타낸다. Reynolds 수가 낮은 영역에서 CASE 6이 가장 높은 무차원 Nusselt 수를 나타냈다. 또한 유속이 커져도 CASE 6에서 가장 높은 열전달 향상을 볼 수 있다. 이것은 모든 CASE에서 동일한 펌프동력을 주었을 때 CASE 6의 효율이 가장 우수하다는 것을 보여준다. 즉, CASE 6이 다른 CASE보다 유동저항이 작다는 것을 말해준다.
4. 결 론
수치해석 결과를 실험결과와 비교하여 수치해석의 타당성을 확인하였으며, 립이 설치된 사각채널내에서의 열전달 및 압력강하 특성에 관한 수치해석을 수행하여 다음과 같은 결론을 얻었다.
(1) 사각덕트에 립을 설치하면 립과 립 사이에서 발생하는 유동의 박리와 재부착이 발생하여 매끈한 덕트에 비해서 열전달이 향상된다.
(2) 립에 각도를 주면 주유동이 립을 따라 흘러가게 되므로 아래 벽면에서의 유속이 빠르기 때문에 열전달 성능이 증가하였다.
(3) 립과 립 사이에 그루브를 넣으면 유동의 교란이 더 활발하게 되므로 열전달 성능이 증가하였다. 끊어진 립의 경우 유동저항이 작으므로 마찰인자가 가장 낮았다.
(5) 각도가 60o인 끊어진 립에서 가장 높은 성능계수가 나타났다. 유속의 증가에 따라 모든 CASE에서 열전달 계수가 증가하였으나 압력손실이 증가하면서 성능계수는 줄어들었으며, 낮은 유속에서 성능계수가 가장 높았다.
Acknowledgments
이 논문은 2012학년도 동의대학교 교내연구비에 의해 연구되었음(과제번호:2012AA157).
References
-
G. Tanda, "Heat transfer in rectangular channels with transverse and V-shaped broken ribs", International Journal of Heat Mass Transfer, 47(2), p229-243, (2004).
[https://doi.org/10.1016/S0017-9310(03)00414-9]

-
K. R. Aharwal, B. K. Gandhi, and J. S. Saini, "Experimental investigation on heat-transfer enhancement due to a gap in an inclined continuous rib arrangement in a rectangular duct of solar air heater", Renewable Energy, 33(4), p585-596, (2008).
[https://doi.org/10.1016/j.renene.2007.03.023]

-
R. Karwa, C. Solanki, and J. S. Saini, "Heat transfer coefficient and friction factor correlations for the transitional flow regime in rib-roughened rectangular ducts", International Journal of Heat Mass Transfer, 42(9), p1597-1615, (1999).
[https://doi.org/10.1016/S0017-9310(98)00252-X]

- ANSYS 12.1, FLUENT manual, (2009).
-
W. P. Jones, and B. E. Launder, "The prediction of laminarization with a two-equation model of turbulence", International Journal of Heat and Mass Transfer, 15(2), p301-314, (1972).
[https://doi.org/10.1016/S0017-9310(98)00252-X]

-
S. Mochizuki, "Flow pattern and turbulence intensity in stacks of interrupted parallel-plate surface", Experimental and Fluid Science, 7(1), p51-57, (1988).
[https://doi.org/10.1016/0894-1777(88)90047-7]

-
L. R. Webb, and L. D. Gee, "Forced convection heat transfer in hellically rib-roughened tubes", International Journal of Heat and Mass Transfer, 23(8), p1127-1136, (1980).
[https://doi.org/10.1016/S0017-9310(98)00252-X]

- A. E. Bergles, A. R. Blumenkrantz, and J. Taborek, “Performance evaluation criteria for selection of enhanced heat transfer surfaces", Proceedings of the fifth International Heat Transfer Conference, Tokyo, 2, p239-243, (1974).