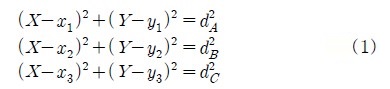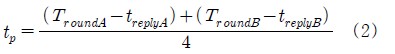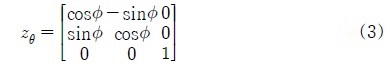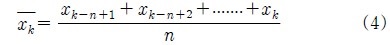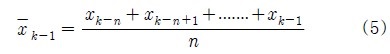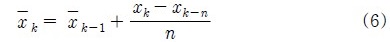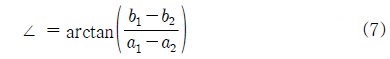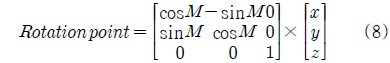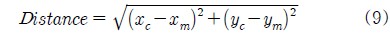Fixed node reduction technique using relative coordinate estimation algorithm

1. 서 론

USN은 무선 통신 기능을 탑재한 소형 디바이스가 다양한 형태의 네트워크를 형성 후 주변 환경 및 위치정보를 획득 및 분석하여 사용자에게 능동적으로 정보를 제공하는 것을 목적으로 한다. 현재 선박의 USN기술은 내부의 온도, 습도 및 압력의 실시간 확인을 위한 모니터링 분야와 승선원들의 안전을 위한 위치인식 분야 등 다방면에서 연구가 활발히 진행되고 있다 [1][2]. 그 중 위치인식 분야의 경우 선박의 특성상 위성으로부터 되돌아오는 전파를 수신하여 거리를 측정하는 GPS(Global Positioning System)의 사용에 어려움이 있다. 따라서 선박의 실내 위치인식을 위해서는 부가적인 유·무선 통신노드의 배치가 필수적이며, 대형 크루즈선이나 연안 여객선과 같이 많은 사람이 이용하는 교통수단의 경우 기존의 삼변측량법을 이용하여 이동노드의 수를 줄이고, 고정노드의 수를 늘리는 것이 USN환경 구축의 비용적인 측면에서 효과적이다. 하지만 LNG 운반선, 탱커선, 컨테이너선 등의 경우 선박의 운항비 중에서 인건비가 차지하는 비율을 최소화하고, Fail-Safe 개념으로 선박을 제어관리 하기 위하여 첨단 자동화 시스템을 탑재하여 운용하고자 함에 따라 승선원들의 수를 최소화하는 실정이며, 또한 공장자동화 및 물류시스템의 발전으로 인하여 인력을 절감하고 있는 추세이다[3][4].

Seong et al. [5]은 이변측위기법을 이용하여 고정노드의 수를 줄이고 또한 전파의 반사와 회절에 의한 거리 오차가 변동하는 코너 구간에서 초전센서를 이용하여 이동구간의 위치를 인식하였다. 실험결과 일반적인 방법대비 86.2%의 선내 위치인식 정확도와 효율이 향상됨을 보였다. 하지만 수 미터 내외의 좁은 복도환경을 고려하여 이동노드가 복도 중앙에 있다는 가정 하에 실험이 진행되어 좁은 통로가 아닌 넓은 공간에는 적용하기 어려운 단점이 있다.

Park [6]은 복도환경에서 고정노드의 수를 줄이기 위해 초음파 센서로 하여금 현 위치에서 복도 양쪽 옆면까지의 거리를 측정하여 사용자를 복도 중앙으로 유도한 후 이변측위기법을 이용하여 위치를 추정하였다. 실험결과 기존의 삼변측량법의 경우 거리 오차 평균이 최대 4m인 반면 제안된 방법의 경우 1.5m로 개선된 성능을 확인할 수 있다. 하지만 사용자가 복도 중앙으로만 통행해야하는 불편함이 존재한다.

Kim et al. [7] 등은 기존의 크리켓 위치인식 방식에 관성 센서를 추가하여 고정노드 수를 줄이는 경제적인 방법을 제안하였다. 하지만 최종 실험은 컴퓨터 시뮬레이션으로 진행되어 실제 환경변수에는 어느 정도 강인한지 확인할 수 없다.

본 논문에서는 기존의 IEEE 802.15.4a UWB 신호와 SDS-TWR(Symmetric Double Sided-Two Way Ranging)기반의 위치추정 방식을 근거로 하여 고정노드의 개수를 감소시키는 알고리즘을 제안한다. 제안한 알고리즘의 성능분석을 위해 고정노드 2개와 이동노드 3개를 이용하였다. 초기 일정간격으로 배치된 이동노드의 임의의 좌표를 기준으로 고정노드의 상대좌표를 추정 후 그 고정노드 중 이동노드에 근접한 노드를 선택하여 그것을 중심으로 추정된 고정노드의 기울기와 실제 고정노드의 기울기의 차만큼 회전한다. 그 후 회전 중심 고정노드를 실제 고정노드위치로 이동한다. 제안한 알고리즘은 7m×8m 의 실내 자유공간에서 실험을 통해 그 성능을 입증하였다.

2. 관련이론

2.1 삼변측량법

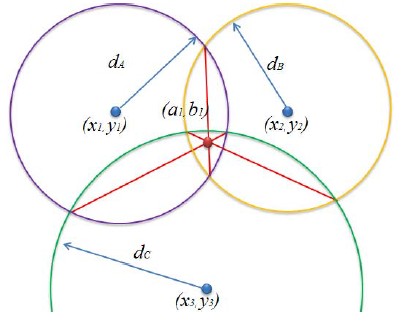
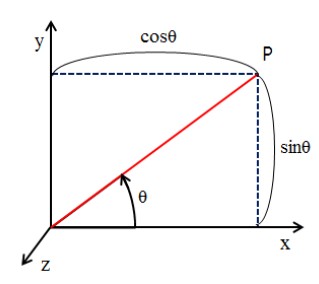
삼변측량법은 비컨 노드들과의 거리를 이용하는 Lateration 기법을 사용하거나 비컨 노드와의 각도를 이용하는 Angulation 기법을 통해서 센서 노드의 위치를 측정한다. Lateration 기법은 별도의 하드웨어 지원 없이도 신호의 TOF(Time of Flight)나 신호의 세기를 가지고 거리를 측정할 수 있어서 많이 이용된다. Figure 1에서 각 고정노드의 좌표값을 알고 이동노드와 고정노드 사이의 거리를 알고 있다면 이동 노드의 좌표는

를 연립하여 획득한 교점의 좌표를 잇는 선들의 교점을 이용하여 위치를 추정한다.

Figure 1:

Schematic diagram of trilateration

2.2 SDS-TWR

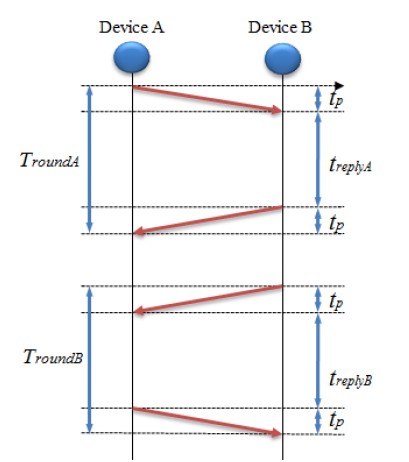
TWR은 Figure 2에 Device A와 Device B 사이의 거리를 추정하기 위해서 노드간 송수신 시간을 측정하는 방식을 의미하며, 정확도 향상을 위해 TWR을 두 번 반복하는 것을 SDS-TWR이라고 한다. 이때 두 노드는 동기화되지 않은 별도의 클럭을 사용한다. SDS-TWR방식을 이용한 거리 측정방법은 먼저 Device A에서 Ranging Message 전송이 시작되는 시간을 기록하고 Device B로 전송한다. Device B에서는 Ranging Message 수신시간을 저장하고 t_replyA만큼의 시간을 기다린 후 다시 Device A에게 Ranging Message를 보낸다. 여기에서 t_replyA는 t_p보다 더 길게 설정 한다. 마지막으로 Device B는 자신이 측정한 시간을 Device A에게 모두 전송한다. 여기서 시간은

과 같이 표현될 수 있다.

Figure 2:

SDS-TWR

2.3 좌표의 회전변환

Figure 3과 같이 z축 기준으로 P₁(1,0,0)을 θ만큼 회전 시킬 경우, 삼각함수의 기본 공식에 의해 x = cosθ, y = sinθ, z = 0으로 변환하며, P₂(0,1,0)를 θ만큼 회전 시킬 경우 x = cos(θ + π/2), y = sin(θ + π/2), z = 0 즉, x = -sinθ, y = cosθ으로 변환한다. P₃(0,0,1)의 경우 회전축 이므로, x = 0, y = 0, z = 1이 그대로 유지 된다. 각 점들을 열 기준 행렬로 표현 하면,

과 같이 오일러 각도 변환 중 z-축 기준 행렬 값 을 얻을 수 있다.

Figure 3:

Rotation of coordination

3. 제안한 위치추정 알고리즘

3.1 고정노드 위치추정을 위한 RE 기법

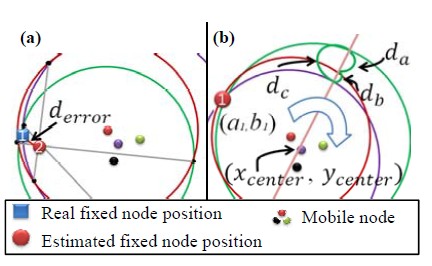
제안한 위치추정 알고리즘에 Figure 1과 같이 기존의 삼변측량법을 사용할 경우 각 노드로부터 수신된 거리가 멀어짐에 따라 원주의 증가 및 무선통신 거리측정 장치의 내재적 오차로 인하여 Figure 4 (a)와 같이 실제 고정노드의 위치는 1에 있지만 2의 위치로 인식하는 경우가 발생한다. 또한 추정된 거리 값을 이용해 형성된 각 원의 교점이 발생하지 않을시 위치를 추정하기 어려운 단점이 있다. 따라서 본 논문에서는 Figure 4 (b)와 같이 새로운 RE 기법을 이용하여 고정노드와 이동노드 사이의 추정된 거리 값을 기반으로 형성된 세 원 사이의 거리가 최소인 구간을 선정하는 방식으로 위치 추정오차를 개선하였으며, 또한 기존의 삼변측량법을 본 논문에서 제안한 위치추정 알고리즘에 적용하였을 경우 발생하는 위치 추정오차를 개선하였다. Figure 5는 RE 기법의 블록 다이어그램을 나타낸다. 먼저 고정노드로부터 수신된 거리 값을 기준으로 형성된 각원과 일정한 간격으로 배치된 이동노드의 중점 (x_center , y_center)을 지나는 직선을 1도 간격으로 회전하여 직선과 원의 교점을 구한다. 회전된 직선과 각 원의 교점사이의 거리 d_a, d_b, d_c의 합이 최소인 구간을 고정노드의 추정 위치로 인식한다. 마지막으로 원주가 증가할수록 UWB의 내재오차로 인한 추정위치의 변동을 줄이기 위해 초기에는 평균값을 이용하였으나, 오래된 데이터가 위치추정에 영향을 미치게 되므로 사용자의 동적인 변화를 반영하는 이동평균 필터를 적용하였다. RE 기법에 의해 획득한 데이터를 x라고 할 경우 평균 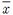는

와 같으며, 식 (4) 이전 평균은

와 같이 구해지며, 식 (4)와 식 (5)의 차를 이용해 식 (6)이 얻어진다.

Figure 4:

Schematic of (a) an estimation error of trilaterlation and (b) a novel RE Technique

Figure 5:

The block diagram for proposed RE technique

3.2 제안한 위치추정 알고리즘

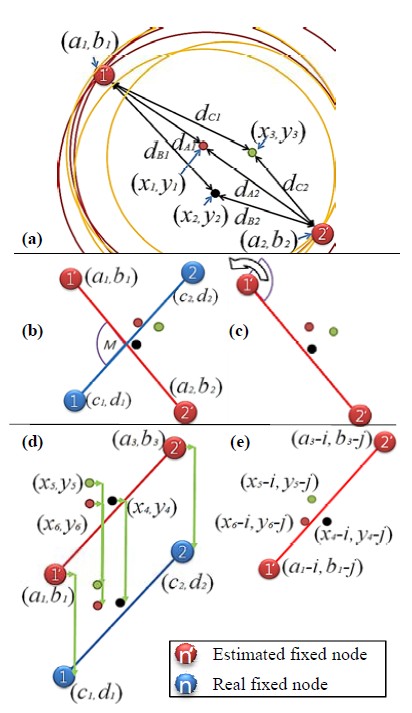
Figure 6의 변수는 아래와 같이 정의하였다.

(x_n , y_n) : 이동노드 n의 기준좌표

(a_n , b_n) : 추정된 고정노드 n의 좌표

(단, (a₃ , b₃)는 (a₂ , b₂)의 회전 후 좌표)

(c_n , d_n) : 실제 알고 있는 고정노드 n의 좌표

(i, j) : (a₁-c₁ ,b₁-d₁)

d_An : 고정노드 n과 (x₁ , y₁)사이측정 거리

d_Bn : 고정노드 n과 (x₂ , y₂)사이측정 거리

d_Cn : 고정노드 n과 (x₃ , y₃)사이측정 거리

M : 추정 고정노드 1′, 2′를 잇는 선과 실제 고정노드 1, 2를 잇는 선의 각도 차

기존의 방식은 고정노드가 이동노드의 위치를 추정하는 반면 제안한 알고리즘은 이동노드를 기준으로 고정노드의 상대좌표를 추정하는 새로운 방법이다. Figure 6 (a)은 일정한 간격으로 배치되어 있는 임의의 이동노드 (x₁ , y₁), (x₂ , y₂), (x₃ , y₃)가 고정노드 1(a₁ , b₁)과 고정노드 2(a₂ , b₂)로 거리 값을 요청한 후 획득한 거리 값 d_An, d_Bn, d_Cn과 제안한 RE 기법을 이용하여 고정노드를 추정하는 장면을 나타내며, Figure 6 (b)는 편의상 Figure 6 (a)의 추정된 고정노드(1′, 2′,붉은색)와 실제 고정노드(1, 2, 파란색)를 간략화 하여 함께 표시하였으며, 추정된 고정노드를 잇는 선의 기울기(∠)는 식 (7)로 표현된다

동일한 방법으로 식 (7)을 이용하여 실제 고정노드를 잇는 선의 기울기를 구한다. 여기서 실제 고정노드는 이동노드의 방향 및 실제좌표를 추정하기 위해 사용된다. Figure 6 (c)는 붉은색 1번을 중심축으로 아래 식(8)을 이용하여 추정된 고정노드 선과 실제 고정노드 선의 차인 각도 M만큼의 회전을 나타낸다.

이때, 회전의 중심은 노드간 거리가 증가할수록 오차가 증가하는 특징을 보완하기 위하여 아래 식 (9)에 의해서 두 개의 고정노드 중에서 이동노드와 근접한 고정노드를 선택한다.

여기에서 x_c와 y_c는 세 개의 이동노드의 중심좌표를 나타내고 x_m과 y_m은 상대좌표로 추정된 고정노드 좌표를 각각 나타낸다. Figure 6 (d)와 같이 회전 후 얻은 새로운 이동노드의 좌표(x₄ , y₄), (x₅ , y₅), (x₆ , y₆)와 추정된 고정노드 2 (a₃ , b₃)의 좌표에서 회전 중심인 추정된 고정노드 1과 실제 고정노드 1의 거리만큼 x, y축으로 좌표를 이동 한다. 이는 추정된 고정노드가 임의의 좌표 값을 가지고 있기 때문에 실제 고정노드를 이용해 좌표를 이동해야 비로소 Figure 6 (d)와 같이 실제 좌표 값을 획득할 수 있다.

Figure 6:

Schematic process of proposed algorithm

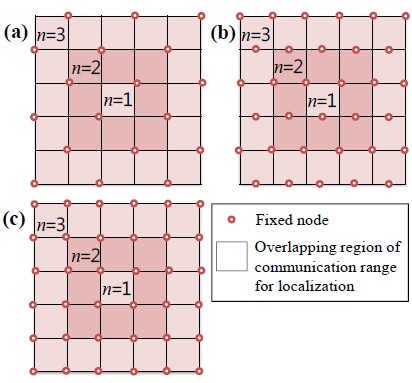
제안한 알고리즘을 이용하여 USN 실내 위치인식 환경구축을 위해 고정노드의 최대 통신도달거리를 고려하여 배치할 경우 Figure 7 (a)와 같이 제안한 알고리즘은 n=1(1×1)부터 n=3(5×5)까지 위치인식 범위가 넓어짐에 따라 2×n²개의 고정노드가 추가되는 반면, 기존의 방법에서 고정노드 3개를 이용하는 Figure 7 (b)의 경우는 4×n²-n개, 고정노드 4개를 이용하는 Figure 7 (c)는 4×n²개의 고정노드가 필요하다. 따라서 본 논문에서 제안한 알고리즘을 실내 위치인식 환경구축에 적용할 경우 기존 방법에 비하여 최대 50%의 고정노드 개수 저감효과를 나타낸다.

Figure 7:

The deployment of fixed nodes using (a) proposed estimation algorithm, (b) trilateration, (c) multilateration

4. 실험 및 고찰

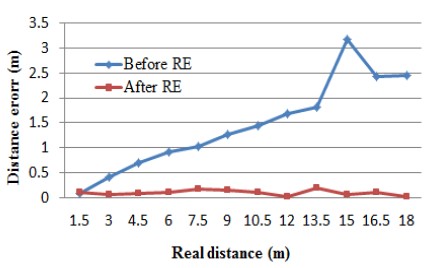
실험은 IEEE 802.15.4a기반의 UWB 통신을 통해 정밀한 거리인식이 가능하고, CRE(Coarse range estimation)방식을 적용하여 다중경로에 강한 Time domain사의 P410RCM 모듈을 이용하여 거리측정을 수행 후, RS-232 직렬통신을 통해 PC로 측정데이터를 전송하여 Visual studio 2008 C# 환경에서 수신된 데이터에 제안한 알고리즘을 적용하였다. 본 논문에서 제안한 RE기법의 신뢰도 확인을 위해 실외 자유공간에서 1.5m부터 18m까지 1.5m간격으로 위치를 변경하며 실험을 진행하였다. 실험 결과 Figure 8과 같이 기존의 삼변측량법을 제안한 알고리즘에 적용하였을 경우 1.5m 거리에서는 오차율 5.67%로 정밀한 위치추정을 하였으나, 그 이후 거리가 증가할수록 내재적 오차 및 환경적 잡음으로 인하여 위치오차는 증가하였으며, 평균 14.08%의 오차율을 보였다. 반면에 본 논문에서 제안한 RE기법을 제안한 알고리즘에 적용하였을 경우 거리에 큰 영향을 받지 않고 평균 거리 오차율 1.28%로 삼변측량법 대비 90.9% 개선된 결과를 획득할 수 있었다. 또한 제안한 RE기법을 기반으로 한 위치추정 알고리즘의 신뢰도 분석을 위해 Figure 9과 같이 7m×8m 실내 강의실의 Fixed node.B와 Fixed node.D부분에 고정노드 2개를 위치시킨 후 노드 3개로 구성된 이동노드를 이용하여 가로1.2m, 세로 1.6m 마다 위치를 변경하며 실험을 진행한 결과를 Figure 9의 붉은 점으로 표시하였다. 동일한 조건에서 기존의 삼변측량법의 성능을 확인하기 위해 각 모서리 부분에 고정노드 4개를 설치하고 이동노드 1개를 사용하여 진행한 결과를 Figure 9의 녹색 점으로 나타내었다. 실험결과 기존 삼변측량법의 경우 위치별 평균 오차가 0.1m로 실내 LOS(Line of Sight)상황에서 높은 견고성을 나타났으며, 제안한 고정노드 2개만을 이용하는 알고리즘의 경우 0.15m로 기존 삼변측량법과 대등한 위치추정 결과를 획득하였다.

Figure 8:

The experimental results for distance error of proposed RE technique and trilateration

Figure 9:

The experimental results for two cases in the indoor environment

5. 결 론

본 논문에서는 고정노드의 수를 효과적으로 줄이기 위하여 노드 3개로 구성된 이동노드를 이용하여, 고정노드 2개의 상대좌표를 추정한 후 이동노드의 위치를 추정하는 알고리즘과 그 과정에서 새로운 RE기법을 제안하여 적용하였다. 제안한 RE기법의 유효성 입증을 위해 실외 자유공간에서 실험결과 기존대비 평균 90.9%의 성능향상을 보였으며, 제안한 알고리즘의 경우 실내 자유공간에서 평균 거리 오차가 0.15m로 고정노드 4개를 이용하는 방법과 대등한 위치 인식 견고성을 보였다. 향후 산업의 고도화 및 자동화를 통하여 소수의 작업자가 관리하는 넓은 장소에 USN 환경을 구축할 경우 제안한 알고리즘 통하여 노드배치 시 상당한 비용절감 효과가 기대된다.

Acknowledgments

이 논문은 2011년도 정부(교육과학기술부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 20110029766).

References

• S.-Y. Choi, "Research for applying IEEE 802.15.4 to indoor location positioning and communication system of ship", M.S. dis-sertation, Inha University, Inchen, (2010), (in Korean).
• C.-U Lee, D.-Y. Lee, Y.-H Yu, and O.-K Shin, "Development of embedded vessel monitoring system using NMEA2000", Journal of the korean society of marine engineering, (2009), 33(4), p746-755, (in Korean). [https://doi.org/10.5916/jkosme.2009.33.5.746]
• J.-S. Ko, B.-R Yu, and J.-H. Lee, "Development process of ship automation", Journal of the korean society of marine engineering,, 27(5), p575-582, (2003), (in Korean).
• M.-S Lee, "A warehouse integration and productivity improvement using logistics automation", M.S. Dissertation, Yeungnam University, Daegu, (2009), (in Korean).
• J.-H. Seong, J.-H. Choi, J.-S. Kim, and D.-H. Seo, "An experimental study on compensation algorithm for localization using modified bilateration technique and pyroelectric sensor in a ship", Journal of the korean society of marine environment & safety, 18(5), p488-495, (2012), (in Korean). [https://doi.org/10.7837/kosomes.2012.18.5.488]
• Y.-K. Park, "A high-precision indoor localization technique using ultrasonic and/or IEEE 802.15.4a based bilateration", M.S. dissertation, Daegu University, Daegu, (2009), (in Korean).
• B.-K. Kim, W.-V. Park, J. Kim, C.-G. Song, and Y.-W. Ko, "Indoor positioning system using inertial sensor and cricket", Journal of Korea Institute of Information Technology, 9(5), p17-24, (2011), (in Korean).