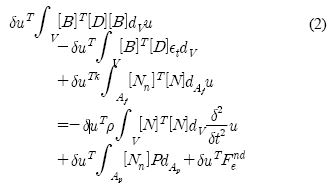Stress analysis of bucket rotating part of the compact excavator

1.서 론

소형 굴삭기는 정격하중 3톤 미만의 굴삭기로 버킷 적제용량은 0.02 ~ 0.1m³ 범위가 일반적이다. 우리나라에서는 일본을 통해 기술이전을 받아 현재는 많은 굴삭기 제작업체가 생산 중에 있으며, 특히 최근에 급격히 증가되는 중국수요 때문에 소형 굴삭기는 주요 수출 종목 중의 하나로 평가되는 건설 장비이다.

소형 굴삭기는 건설현장 뿐만 아니라 농업, 축산업, 광업 분야에서 인력으로 하기 힘든 다양한 작업, 특히 대형장비를 이용하기에 부적합한 좁은 공간에 투입되어 복잡한 작업을 수행하기도 하는데, 이와 같이 협소한 공간에서 굴삭기 전체를 움직일 경우 벽에 부딪치거나 지지하는 지면의 형태에 따라 굴삭기를 원하는 대로 움직이기 어려워 많은 시간을 소비하는 경우가 발생한다. 이때, 굴삭기 착․탈형 부착기구인 버킷을 자유롭게 좌우 360도 이상 회전할 수 있다면 굴삭기 전체를 움직여야하는 복잡한 작업도 원하는 각도만큼 버킷을 회전시켜 좁은 공간에서 신속하게 정교한 작업을 수행할 수 있어 생산성 향상과 에너지 절약에도 큰 도움을 줄 수 있다. 회전형 버킷을 소형 굴삭기에 적용하기 위해서는 버킷을 좌우 360도 이상 회전시킬 수 있는 유압장치와 작업하중을 견딜 수 있는 프레임 설계를 수행하여야 하는데, 본 논문에서는 암, 버킷 그리고 회전형 부착기구의 구조적 안전성을 CAE를 활용하여 확인하고자 하였다[3][5].

2. 해석 이론

굴삭기 구동부 해석은 붐, 암, 버킷을 구성성분으로 하는 3자유도 작업 장치로 모델링하여 해석하는 경우가 대부분으로, 3자유도 작업기로 가정한 굴삭기의 각 관절과 버킷의 끝점 사이의 관계를 정의함으로써 정위치 및 역위치 해석을 수행하게 된다. 본 연구 대상인 버킷 회전부를 가진 소형 굴삭기는 암과 버킷 사이에 회전형 부착기구가 추가되기 때문에 기존의 굴삭기 해석 모델에 자유도가 하나 더 추가되게 된다. 그러나 버킷의 회전은 붐, 암, 버킷의 기구학적 모델과는 완전 독립이고, 버킷 회전에 따른 변화가 붐, 암, 버킷의 기구학적 모델의 정적 및 동적 해석에 미치는 영향은, 무게중심의 변화가 대단하지 않기 때문에 물리적으로 무시 할만하다[1]-[3][5]. 따라서 본 연구에서는 붐, 암, 회전형 어태치먼트 및 버킷의 4요소의 자유도 전부를 고려하지 않고, 암과 회전형 부착기구 그리고 버킷의 상관관계만을 고려하여 해석을 수행하였다.

상용해석 프로그램에서 구조매트릭스는 상용해석 프로그램의 응력-변위량 상관관계와 식 (1)의 관계에 의해 식 (2)와 같이 나타난다.

δ U = δ V      (1)

여기서,

[B] : strain-displacement matrix

[D] : elasticity matrix

F : force vector

k : foundation stiffness in units of force per length per unit area

[N] : matrix of shape functions for normal motions at the surface

P : pressure vector

u : displacement vector

U : strain energy, J

δU : virtual internal work

V : external work, W

δV : virtual external work

이산화한 식 (2)를 풀기 위하여 부품 간 연결은 모두 완전체결된 것으로 가정하여 Block Spare solver를 적용하였다.

Block Spare solver는 Block Lanczos 방법을 체적 응력해석에 적용하는 가장 기본적인 solver로 진동과 파손을 포함하는 응력해석과 일부 열적해석에 사용된다. Lanczos 방법은 1949년 헝가리의 Cornelius Lanczos에 의해 개발된 반복방법(Iteration method)으로 정사각 행렬의 고유치와 고유벡터를 찾는, 발전된 형태의 Power 방법의 일종이다. Lanczos 방법은 필요한 고유치 혹은 고유벡터를 찾기 위해 저차 행렬방정식으로 고유치 행렬방정식을 축소하여 계산하는 방법으로 축소하고, Guess 소거법을 이용하여 고유치와 고유벡터를 구하였다. 수렴속도가 비교적 빠르고 수렴이 될 경우 이론값과 유사한 해석 값을 구할 수 있다는 장점이 있으나, 경계조건에 따라서는 사용하기 어려운 모델이 존재한다는 단점이 있다[6]. 본 연구에서는 탄성 진동체 해석을 수행하기 전 과정으로서 단순화한 모델에 대한 응력수준을 예측하기 위해 해당 solver를 이용하였다. 해석모델 내에 운동부품이 없다고 가정하였으므로 열적해석은 수행하지 않았다[1].

상대운동이 활발한 회전형 부착기구의 경우에는 부품 간 연결조건이 일체화 되었다고 가정할 수 없으므로, 단일부품에 대한 추가해석을 진행하였다. 단, 이 경우에도 열에 의한 영향은 고려하지 않았다. 회전형 부착기구의 해석에 있어서 비선형 요소를 최소화하기 위하여 유압모터의 회전속도(rpm)가 일정하다고 가정하였으며, 이때의 회전수를 경계조건으로 두고 해석을 수행하였다. 이 경우에도 축계 진동해석은 생략하였는데 이는 추후에 이루어질 예정이다.

건설용 중장비의 경우, 기계의 정밀도에 대한 기준은 양호한 반면, 안전율에 관해서는 엄격한 기준을 가지고 있는 것이 보통이다. 안전율(S)은 식 (3)과 같이 나타내며, 극한값으로 볼 수 있는 충격하중에 대한 안전율은 12이다.

여기서,

σ_α : allowable stress

σ_ω : working stress

안전율 선정에는 여러 방법이 있으나 일반적으로 기계설계 시에 적용되는 동적 안전율 3~9를 사용한다. 특히 피로나 크리프에 대한 문제가 있을 수 있는 중장비에서는 비교적 큰 값의 안전율을 요구하는 경향이 있다.

3. 격자구성 및 응력해석

3.1 격자 구성

여러 개의 관절을 가진 굴삭기의 경우 해석 자세를 선정하는 작업이 매우 중요하다. 본 연구에서는 버킷 회전부를 특성으로 하는 소형 굴삭기를 다루기 때문에 버킷 회전을 고려한 다양한 위상에 대해 응력해석을 수행하였지만 버킷의 회전운동에 있어서 차별화된 역학적 상관관계가 미미한 붐은 응력해석 영역에서 제외하였다[4][5].

또한 시간과 메모리의 문제를 최소화하기 위하여 전체 조립체에 대한 응력해석의 경우 각 부품을 모두 조립하여 하나의 구조물로 대체함으로써 간소화 모델을 구축하였다.

상대운동이 활발한 회전부의 경우 해석을 추가적으로 수행하였기 때문에 해당부분의 격자구성을 따로 하였다. 회전형 부착 기구는 모든 부품을 완전체결할 수 없기 때문에 비선형 요소를 고려하여 더욱 작은 메시크기(Mesh size)를 설정하여 격자구성을 하였다.

Figure 1

Grid Generation

Figure 1은 생성된 격자를 나타낸 것으로 (a)는 버킷, 회전형 부착기구 및 암 전부를 격자구성한 모습을 나타내었으며, (b)는 회전형 부착기구만을 분리하여 따로 격자구성을 한 모습이다. 격자구성에는 Patch conforming/sweeping 기법을 사용하였으며, (a)는 총 Node 수 113,225 (b)는 총 Node 수 61,941로 구성하였다.

3.2 응력 해석

암과 버킷, 회전형 부착기구를 모두 포함한 응력해석에는 개발된 회전형 부착기구가 장착된 소형 굴삭기의 상용 작동압력인 120 kg/cm²를 기준으로 하여 산출한 응력 값을 경계조건으로 사용하였다. 암을 고정시키고 비선형 요소를 축소하기 위하여 각 위상별로 부품을 모두 조립하였다고 가정하여 하나의 강체구조로 모델링하였다. 유압계통에서는 열 특성이 중요할 수 있으나, 회전형 부착기구를 제외한 부품에서는 열 발생이 크지 않으며 열로 인한 응력특성의 변화가 없는 것으로 가정하였다.

개별 부품인 회전형 부착기구의 경우 유압모터의 회전속도(rpm) 값을 측정하여 경계조건으로 하고 여기에 버킷의 자중을 추가적으로 부가하였다. 전체를 하나의 강체구조로 가정할 수 없기 때문에 간소화 해석의 정확도의 향상을 위해 외접형 휠 기어의 지지베어링 축은 해석에서 제외하였다. 회전부품에서는 다소 열이 발생하지만 건설기계의 특성상 대기와의 열교환이 활발하며 냉각계통이 존재하기 때문에 열적영향은 크지 않을 것으로 가정할 수 있다.

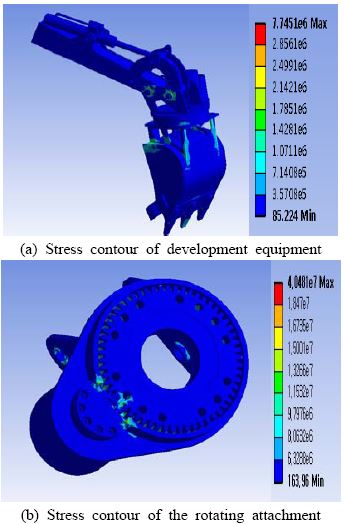
응력해석 결과는 Figure 2의 (a)와 (b)에 응력분포도(stress contour)로 나타내었다. (a)의 경우, 대부분의 영역에서는 85 Pa의 낮은 응력수준을 나타내고 있지만, 유지 및 보수작업을 위한 공동이 존재하는 버킷과 회전형 부착기구의 연결부위에서는 형상에 의한 응력집중으로 인해 다소 높은 능력이 나타났다. 이는 버킷과 연결부품의 체결부위와 핀으로 연결되는 버킷 구동부에서도 동일하게 나타나며 이때의 응력은 약 1 MPa이다. 가장 높은 응력이 나타나는 부분은 핀과 버킷 구동부의 상대운동이 일어나는 부위에서는 7.7 MPa정도임을 알 수 있었다.

회전형 부착기구만 따로 계산한 (b)의 경우에서는 상대운동 부위인 피니언과 외접 휠 기어의 치면 접촉점에서 40 MPa 정도의 높은 응력이 나타났으며, 역시 상대운동 부위인 회전형 부착기구의 케이스와 외접 휠기어의 치면 접촉점에서 높은 수준의 응력을 유지하였다. 전체 해석과는 달리 중력의 영향을 고려하였기 때문에 버킷의 자중 만큼 하중이 추가되어 응력수준이 낮은 부분도 전체해석의 경우 보다 높은 응력 값을 나타내었다. 또한 자중에 의한 영향으로 케이스의 핀 체결부위에서 응력집중이 일어나 다른 부위보다 다소 높은 응력을 나타내었다.

Figure 2

Stress contours

4. 결 론

건설기계는 기계의 정도에 대한 요구 값은 상대적으로 낮은 반면 안전율에 있어서는 상당한 수준을 요구하는 경향이 있다. 굴삭기의 경우 토질에 포함된 석괴 등으로 인하여 높은 하중을 받을 우려가 충분하다. 하지만 재료의 항복강도를 고려하면 최고치를 고려하더라도 응력해석 결과에서 보이는 응력수준은 크지 않은 것으로 나타났다.

유한요소법을 통한 해석결과 대부분의 부분에서는 85 Pa의 낮은 응력수준을 유지하였으나, 조립 및 유지보수를 위한 공동이 있는 회전형 부착기구와 버킷 간의 연결부품 및 체결부위에서 응력집중으로 인해 비교적 높은 하중에 노출되는 것으로 나타났다. 가장 높은 응력이 나타난 곳은 상대운동이 있는 핀 체결부위로 다른 부분에 비해서 100,000배 정도 높은 7.7 MPa 정도의 응력이 나타났다.

회전형 부착기구의 개별 해석에 있어서는 기어의 접점에서 국부적으로 40 MPa 정도의 높은 응력이 나타나며 이는 해석 부품 전체를 통틀어 가장 높은 값이지만 주어진 안전율에서 사용이 가능함을 알 수 있었다.

Acknowledgments

본 연구는 2011년 산학연 공동기술개발사업의 일부지원(과제명 : 소형 굴삭기용 회전형 버킷 개발)에 의하여 수행되었음을 밝힙니다.

References

• ANSYS Inc, ANSYS User`s Guide, 12, (2010).
• D.-H. Han, Kim H.-G., and Lee B.-J., “Load handling and dynamic performance analysis for the excavator”, Proceedings of The Korean Society of Mechanical Engineers, 2(1), p585-590, (1995).
• J.-M. Choung, Kim G.-S., Jang Y.-S., Choe I.-H., and Heo M.-S., “Study on the static and dynamic structural analysis procedure of excavators”, Proceedings of The Korean Society of Mechanical Engineers, p537-543, (2003).
• Kwon S.-K., “Dynamic model development and simulation of crawler type excavator”, The Korean Society of Machine Tool Engineers, 18(6), p642-651, (2009).
• S.-Y. Kim, Lee J.-O., Kim B.-J., and Baek S.-J., “Working simulation of a shovel-typed excavator using flexible multi-body dynamics”, The Korean Society of Mechanical Engineers, 33(5), p60-64, (in Korean).
• Carlos, "Lanczos-Lovelock and f(R) gravity from clifford space geometry", International Journal of Theoretical Physics, 52(1), p28-41, (2012).