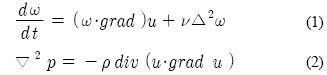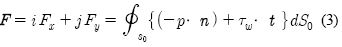Characteristic calculations of flowfield around a square prism having a detached splitter plate using vortex method
The characteristics of the unsteady flowfield of a square prism having a detached splitter plate at the wake side were investigated by advanced vortex method. The instantaneous and average velocity field and pressure field around a square prism without and having splitter plate were calculated by forcing the gap ratio having the maximum drag reduction rate, at Reynolds number Re=1.0×104 and the width ratio H/B=1.0 of splitter to the prism width. The drag and lift coefficients on the square prism were also obtained. The calculated results agree with the measured drag coefficients and pressure distributions on the square prism. The vortices of the opposite direction at upside and down side of the splitter plate were generated by installing of the plate. And the drag on the square prism was decreased by increasing of the pressure of back face of the prism with the vortices.
초록
본 연구는 정방형주의 후류측 중심에 분리된 분할판(Detached splitter plate)을 설치한 경우 정방형주의 주위의 유동장을 최신와법으로 파악한 것이다. 레이놀즈 수 Re=1.0×104 및 분할판의 폭을 정방형주 한변의 길이(B)로 고정시키고, 특히 항력감소율이 최대인 간격비에 촛점을 맞추어 분할판 유, 무에 따른 정방형주에 주위의 순간 및 평균 속도장 및 압력장을 시뮬레이션하였고, 양, 항력계수의 시간변화도 계산하였다. 계산결과는 측정된 항력계수 및 압력분포와 잘 일치하였다. 분할판 설치에 의해 분할판의 상하부에 서로 반대방향의 볼텍스가 발생했고, 이 볼텍스가 정방형주 뒷면의 압력을 상승시켜 항력을 감소시켰음을 명확하게 나타냈다.
Keywords:
Vortex method, Unsteady flow, Drag reduction, Square prism, Splitter plate, 와법, 비정상 유동, 항력감소, 정방형주, 분할판1. 서 론
물체에 작용하는 유체력 중에서 유체가 흘러가는 방향으로 작용하는 힘을 항력, 흐름에 수직한 방향으로 작용하는 힘을 양력이라 한다. 물체표면의 유동을 제어하여 물체에 작용하는 항력, 양력 즉 유체력을 저감시키면 유체력에 의한 구조물 파괴의 방지는 물론, 비행기, 자동차, 선박 등은 추진효율이 증가하여 에너지 절감에도 효과가 크다. 그래서 다양한 방법으로 물체주위의 유동장을 제어해서 유체력을 저감시키는 연구가 진행되어 왔는데 실용화를 위해서는 유체력 감소율을 크게 함은 물론, 그 방법도 단순하고 쉬워야 한다. 일반적으로 물체주위의 유동을 제어해서 항력을 감소시키는 방법으로 에너지가 부족한 경계층 영역에 외부에너지의 공급유무에 따라 능동적 기법과 수동적 기법으로 나눌 수 있다[1].
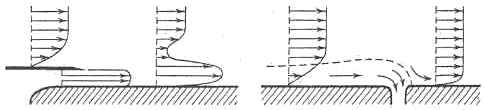
전자는 Figure 1에 나타낸 바와 같이 경계층이 박리하기 직전에 경계층 내 운동 에너지를 보충하던지 아니면 에너지를 소실한 경계층을 흡입해서 하류에 새로운 경계층을 만드는 방법이다.
Principle of active control
반면 후자는 물체의 표면을 유선형으로 하여 압력상승을 완만하게 하는 소극적인 방법과 물체표면에 부가물을 설치하여 경계층 부근의 흐름을 교란시켜 운동에너지가 부족한 물체표면의 흐름이 경계층 외측의 흐름과 혼합해서 박리에 견디는 능력을 증가시키는 적극적인 방법이 있다. 이 방법은 외부에너지 공급 없이 단순히 물체의 기하학적 형상을 변경하거나 간단히 부가장치를 부착하면 되기 때문에 산업현장에 응용하기 쉽다. 후자의 실용적인 예로서 Figure 2에 나타낸 비행기 주 날개 배면의 와류발생기(vortex generator) 등을 들 수 있다.
Vortex generator
한편 정방형주로 대표되는 유체역학 문제로서는 강풍에 노출된 빌딩, 교량, 철도차량 및 컨테이너 트럭과 같은 대형 구조물에서부터 냉각팬 앞에 놓인 반도체 주위의 흐름까지 수없이 많다. 특히 사각주 후면의 와류진동은 대형 구조물의 동적안정성에 심각한 영향을 미치므로 동적안정성 향상과 항력감소를 위해 사각주 주위의 유동장을 제어하는 연구가 활발히 진행되고 있다.
Igarashi[2]는 정방형주의 상류측에 작은 원주봉을 설치하여 정방형주에 작용하는 항력을 현저하게 감소시켰다. Sakamoto et al. [3]는 정방형주의 상류측에 수직평판을 설치함으로서 정방형주에 작용하는 유체력을 억제시킬 수 있음을 실험으로 보였다. Tamura et al. [4]는 사각주 네모서리의 형태를 세 가지로 가공하여 유동장 특성실험을 행한 결과 각진 모서리 보다 둥근 모서리를 가진 정방형주가 항력, 양력특성이 우수함을 보였다. 또한 Park[5]은 정방형주 뒷면 중앙에 분리판을 부착하여 분리판이 항력감소에 미치는 영향을 와류추적법으로 수치계산하였고, 분리판의 길이를 증가시킬수록 항력계수는 작아졌다고 보고했다. Doolan[6]은 레이놀즈 수 Re=150의 저 레이놀즈 수 영역에서 정방형주의 후류측에 부착이 아닌 분리된 분할판(Detached splitter plate)을 설치하는 방법으로는 처음으로 정방형주의 항력저감을 시도했는데 분리판 설치에 의해 정방형주에 작용하는 유체력 즉 항력계수, 양력계수의 진폭을 감소시킬 수 있음을 수치해석적으로 나타냈다. 최근 Ro et al. [7]는 레이놀즈 수 Re=10,000의 고 레이놀즈 수 영역에서 정방형주의 후류측에 분리된 분할판을 설치하여, 정방형주의 항력저감특성을 양, 항력 측정실험으로 파악하였으며, 분할판의 폭을 정방형주 한변의 길이와 같게 했을 경우, 간격비 G/B=0.75에서 최대 19.9%의 항력감소율을 얻었다. 그러나 분할판의 유, 무에 따른 정방형주 주위의 유동장의 변화는 명확하게 파악하지 못하였다.
따라서 본 연구는 전보[7]에 이어 분리된 분할판(Detached splitter plate)을 가진 정방형주의 주위의 비정상 유동장, 압력분포 및 유체력 특성이 분할판의 유, 무에 따라 어떻게 변하는지 최신와법[8][9]으로 명확하게 파악하고자 한다.
2. 계산방법
2.1 해석모델
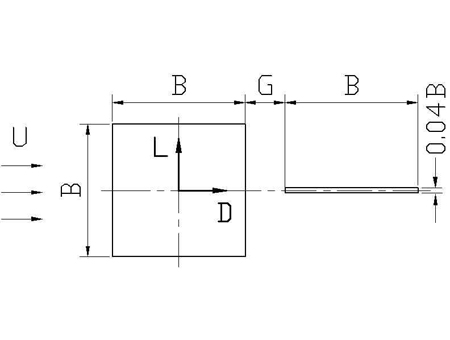
먼저 분리된 분할판을 가진 정방형주의 해석모델을 Figure 3에 나타낸다. 본 해석모델은 계산결과를 실험결과와 비교하기 쉽게 전보의 실험모델과 동일한 모델을 사용하였다. 즉 일정류 U중에 한 변의 길이 B 인 정방형주가 놓여 있고, 그 뒷 벽면 중심에서부터 G만큼 떨어진 곳에 일정류 방향으로 폭 B인 두께 0.04B인 얇은 분할판이 놓여 있다. 이때 정방형주의 항력 D는 일정류와 같은 방향으로 작용하는 유체력 성분을, 양력 L은 일정류와 수직 상방향으로 작용하는 유체력 성분을 의미한다. 일반적으로 일정류 중에 놓인 정방형주 주위의 흐름은 정체, 박리, 재 부착, 2차 박리 현상과 후류에서의 주기적인 칼만 볼텍스로 특정 지어진다. 이 칼만 볼텍스는 분리판의 유, 무에 따라 서로 다른 흐름 특성을 보일 것으로 예상되며, 특히 전보에서 항력감소율이 최대가 되는 간격비 G/B=0.75을 중심으로 분할판의 유, 무에 따른 정방형주에 주위의 비정상 유동장을 명확하게 파악하고자한다.
Analytical model
2.2 최신 와법에 의한 유동장의 계산
와법에 의한 본 유동장 즉 속도장과 압력장의 계산은 Navier-Stokes방정식의 회전으로부터 얻어지는 와도수송방정식 및 발산으로부터 얻어지는 압력 포아손(Poisson)방정식에 기초하고 있다.
여기서 u 및 ω는 각각 속도벡터 및 ω = rot u로 정의되는 와도벡터를 나타낸다. 최신 와법은 즉 윗 식에서 속도는 Biot-Savart law, 압력은 Uhlman [9]에 의해 수식화된 적분방정식을 적용하여 계산한다. 한편 와법에서 유동장에 존재하는 와도의 분포는 유동장 내에 이산와요소를 도입함에 의해 표현된다. 본 유동장 계산에 있어 경계조건 및 방출와의 도입방법, 속도장 및 압력장의 계산방법은 Kamemoto[8]의 해석방법을 그대로 사용했기 때문, 여기서는 그 구체적인 방법은 생략한다.
한편 본 정방형주에 작용하는 유체력 F는 압력 p의 법선성분 및 전단응력 Tw의 접선성분을 물체표면 S0에 따라 전주 적분하여 다음과 같이 계산한다.
여기서 Fx및Fy는 정방형주에 작용하는 x, y방향의 힘의 성분을 나타내며, 각각 Figure 3의 항력 D 및 양력 L에 상당한다.
또한 계산조건은 계산결과와 실험결과[6]와의 비교를 용이하게 하기 위해 같은 조건을 사용하였다. 즉 일정류 U=1, 정방형주 한 변의 길이 및 분할판 폭 B=1, 레리놀즈 수 Re=1.0×104로 했다. 그리고 타임스텝Δt = 0.05간격으로 1,000스텝(Ut/B=50)까지 계산했으며, 아래 계산결과에서 평균 유동장은 1,000스텝까지의 유동장을 시간 평균한 것이다.
3. 계산결과 및 고찰
3.1 정방형주 주위의 유동장 특성
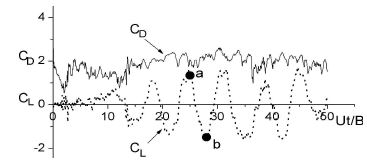
Figure 4에 정방형주에 작용하는 항력계수 CD 및 양력계수 CL의 시간변화를 나타낸다. 그림에서 횡축은 일정류 U에 계산시간 t를 곱한 값을 정방형주 한 변의 길이 B로 나눈 값으로 무차원 시간을 나타낸다. 먼저 항력계수 CD를 보면 시간이 경과함에 따라 다소 진동하지만 그 값이 거의 2.0 전후를 나타내고 있다. 그러나 양력계수 CL은 계산초기에는 그 값이 거의 0에 가까우나 무차원 시간 15이상에서는 횡축을 중심으로 크게 진동하고 있다. 이는 후술하는 Figure 9 (ⅰ)에 나타낸 바와 같이 정방형주의 후류가 계산 초기에는 쌍자와의 형태이나 시간이 경과함에 따라 크게 진동하기 때문으로 추정된다.
Time variations of lift and drag co-efficients on square prism
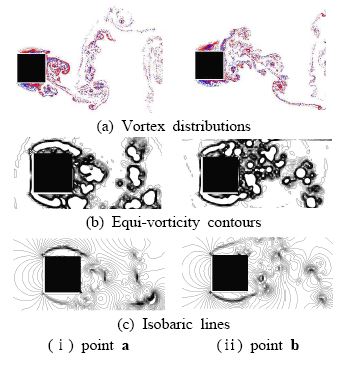
Figure 5에 정방형주에 작용하는 양력계수의 최대, 최소점 즉 Figure 4의 점 a, b에서의 순간적인 유동장을 나타낸다. Figure 5(a)의 볼텍스 분포에서 양력의 최대점 즉 점 a는 정방형주 후면 가까이에 있는 볼텍스가 아래쪽으로 분포되어 있지만 점 b의 경우는 위쪽으로 치우쳐 져있다. 그리고 Figure 5(b) 및 (c)의 등와도선 및 등압력선을 살펴보면 두선 모두 점 a의 경우는 정방형주 전면 상부 모서리에서 흐름이 박리되어 후면의 상부 모서리에 연결되어 있고, 점 b의 경우는 정방형주 하부 모서리에서 흐름이 박리되어 후면의 하부 모서리로 연결되었다. 위에서 살펴본 Figure 5(a), (b) 및 (c)의 흐름패턴에서 정방형주 주위에는 점 a의 경우 시계방향의 순환, 점 b의 경우는 반시계방향의 순환이 존재함을 알 수 있다.
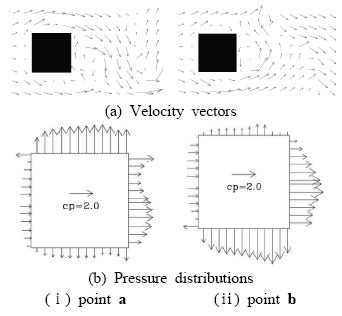
Figure 6에 양력계수의 최대, 최소점 즉 Figure 4의 점 a, b에서 정방형주 주위의 속도벡터 및 압력분포를 나타낸다. 압력분포에서 화살표가 물체방향으로 향하는 것은 정압, 물체와 반대방향으로 향하는 것은 부압을 나타낸다. Figure 6(a)의 속도벡터장을 살펴보면 Figure 5에서 설명한 정방형주 둘레의 순환 즉 점 a의 경우 시계방향의 순환, 점 b의 경우는 반시계방향의 순환이 존재함을 구체적으로 알 수 있다. 이 순환의 방향은 Figure 6(b)의 압력분포와 밀접한 관계가 있다. 즉 점 a의 경우는 시계방향의 순환이 존재하여 정방형주 상면에는 순환에 의한 유속과 일정류의 유속이 같은 방향으로 작용하기 때문 유속이 빨라져 큰 부압이 작용하며, 정방형주 하면에는 순환에 의한 유속이 일정류의 유속과 반대방향으로 작용하게 되어 유속이 감소하여 부압의 절대치가 작음을 알 수 있다.
이와는 반대로 점 b의 경우는 반시계방향의 순환이 존재하여 정방형주의 하면에 큰 부압이, 상면에는 상대적으로 작은 부압이 작용함을 알 수 있다. 여기서 정방형주 주위의 압력계수는 상류측 면의 중심 즉 정체점에서의 압력계수 cp=1.0이므로 각 점에서의 화살표 크기로 유추할 수 있다.
Various flowfields at the point a and b of Figure 4
Velocity vectors and pressure dis-tributions at the point a and b of Figure 4
3.2 분할판 유, 무에 따른 유동장 비교
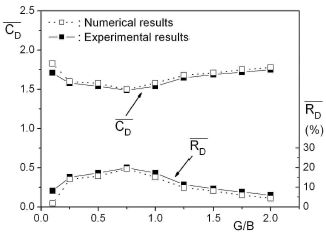
Figure 7에 분리된 분할판을 가진 정방형주의 간격비에 따른 평균항력계수 및 평균항력 감소율을 나타낸다. Figure 7에서 점선은 본 계산에서의 수치결과이며, 실선은 전보[7]에서의 실험결과이다. 항력감소율은 간격비 G/B=0.75에서 최대치를 나타내며 계산결과는 실험결과와 전 간격비에서 잘 일치하고 있어 본 계산법의 정확성을 말해주고 있다.
Average drag coefficients and drag re-duction rates with gap ratios G/B
Figure 8에 분리된 분할판을 가진 정방형주에 작용하는 항력계수 CD 및 양력계수 CL의 시간변화를 나시간변화를 나타낸다. 타낸다. 여기서 분할판의 간격비는 Figure 7에서 항력감소율이 최대인 G/B=0.75의 경우이다. 먼저 항력계수 CD를 보면 그 값이 다소 진동하고 있으나 평균적으로 1.5정도이고, 양력계수 CL 또한 0의 값을 중심으로 진동하고 있으나 그 값은 매우 적다. 이들 양력, 항력계수의 시간변화를 분할판이 없는 정방형주 즉 Figure 4의 각각을 비교해보면 분할판에 의해 항력계수 및 양력계수의 진폭이 대폭 감소했음을 알 수 있다. 특히 양력계수의 진폭 감소는 그 물체의 동적 안전성을 크게 향상시켜 준다.
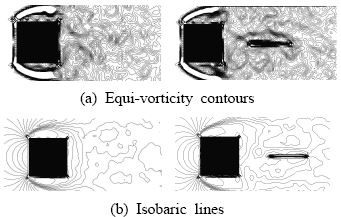
Figure 9는 분할판 유, 무에 따른 정방형주 주위의 볼텍스 분포를 나타낸다. Figure 9에서 계산초기 즉 40스텝에서 볼텍스 분포를 보면 정방형주 앞 모서리에서 박리한 흐름이 뒷 모서리에 연결되어 있고, 뒷모서리 부근에서 2차 박리가 일어나 정방형주 바로 뒷면 부근에 쌍자와를 형성하고 있음 보여주고 있다. 이때 분할판이 이 쌍자와를 상, 하로 분리시키고 있음을 알 수 있다. 충분히 발달된 영역 즉 400에서 볼텍스 분포를 보면 분할판이 없는Figure 9 (ⅰ)의 경우 후류는 일정류와 수직방향으로 진동하고 있지만 분할판이 있는 Figure 9 (ⅱ)의 경우 후류는 분할판을 중짐으로 상, 하가 대칭적으로 나타나 있다.
Figure 10은 분할판 유, 무에 따른 정방형주 주위의 시간평균 유동장을 나타낸다. 그림에서 (a)는 등와도선, (b)는 등압력선을 나타낸다.
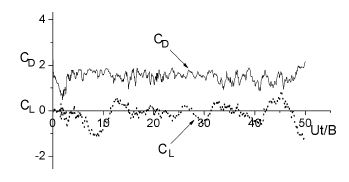
Time variations of lift and drag coefficients on square prism having a detached splitter plate(G/B=0.75)
Vortex distributions around square prism without and having splitter plate
Average flowfields around square prism without and having splitter plate
Figure 10 (ⅰ) 및 (ⅱ)에 나타낸 것처럼 평균 유동장은 분할판 유, 무에 따라 특별한 변화를 보이지 않고 있다. 그러나 정방형주 앞쪽 상, 하 모서리에서의 박리현상으로 등와도선 및 등압력선 모두 앞쪽의 상, 하모서리에서 뒤쪽으로 Figure 5와는 달리 대칭적으로 진하게 나타나 있는데 분할판을 가진 편이 가지지 않는 편보다 그 각도가 다소 크게 나타나 있다.
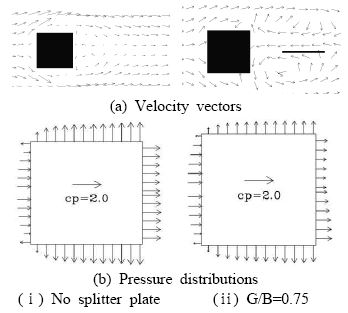
Figure 11은 분할판 유, 무에 따른 정방형주 주위의 시간평균 속도벡터장 및 압력분포를 나타낸다. 먼저 Figure 11(a)의 속도벡터 장의 경우 분할판이 없는 경우 정방형주 후류측에 작은 정체영역이 보이나 분할판이 있는 경우는 분할판의 상, 하에 서로 대칭한 크다란 볼텍스가 형성해 있다. 즉 분할판 상부에는 시계방향의 볼텍스가, 하부에는 반시계방향의 볼텍스가 존재해 있고, 이 두 개의 볼텍스 방향으로 볼 때 정방형주 뒤 쪽에는 역류가 발생하며, 이 역류가 Figure 8 및 Figure 9에서 보인 항력감소의 원인으로 추정된다. Figure 11(b) 정방형주 둘레의 압력분포에서 화살표가 물체 표면으로 향하는 것은 정압, 바같쪽으로 향하는 것은 부압을 나타낸다. 분할판의 유, 무와 관계없이 정방형주의 상류측 면은 정압, 그 외의 면은 부압이 작용하는 것을 알 수 있다. Lee [11]의 실험결과에 의하면 일정류 주에 놓인 정방형주의 경우, 시간평균압력계수 cp는 상류측 면의 중심 즉 정체점에서는 cp=1.0, 상, 하면에서는 cp=-1.4 그리고 하류측 면에서는 cp=-1.2로 나타내고 있어 계산결과는 실험결과와 정량적으로도 비교적 잘 일치하고 있다. 또한 분할판의 유, 무에 따라 압력분포의 크기를 비교해보면 일정류 방향으로 정방형주의 상류측 면의 화살표 길이는 Figure 11 (ⅰ) 및 (ⅱ) 양쪽 모두 비슷한 크기를 가지나, 하류측을 보면 분할판이 있는 쪽이 없는 쪽 보다 화살표 길이가 특히 중앙 부근이 더 짧게 나타나 있어 앞서 설명한 역류에 의한 압력증가의 타당성을 잘 설명하고 있다. 그리고 분할판의 유, 무에 따라 상, 하면의 압력분포를 비교해 보면 분할판이 있는 쪽이 없는 쪽 보다 화살표 길이가 짧게 나타나 있어 Figure 4 및 Figure 8에 보인 것 처럼 분할판을 설치함으로써 정방형주 상, 하면의 압력변동을 억제하여 양력의 진폭을 줄일 수 있음을 알 수 있다.
Average velocity vectors and pressure distributions around square prism without and having splitter plate
4. 결 론
본 연구는 정방형주의 후류측 중심에 분리된 분할판(Detached splitter plate)을 설치한 경우 정방형주의 주위의 유동장을 최신와법으로 파악한 것이다. 레이놀즈 수 Re=1.0×104 및 분할판의 폭을 정방형주 한변의 길이(B)로 고정시키고, 특히 항력감소율이 최대인 간격비에 촛점을 맞추어 분할판 유, 무에 따른 정방형주에 주위의 순간 및 평균 속도장 및 압력장을 시뮬레이션하였고, 양, 항력계수의 시간변화도 계산하였다. 정방형주에 작용하는 양력의 최대점 및 최소점에서의 순간 볼텍스 분포, 등와도선, 등압력선, 속도벡터장 및 압력분포를 명확하게 가시화하였고, 이들 유동장의 변화는 정방형주 주위의 순환으로서 설명가능했다. 또한 분할판 유, 무에 따른 평균 속도장 및 압력장의 변화를 계산하였으며, 분할판 설치에 의해 분할판의 상하부에 서로 반대방향의 볼텍스가 발생했고, 이 볼텍스가 정방형주 뒷면의 압력을 상승시켜 항력을 감소시켰음을 명확하게 나타냈다.
Acknowledgments
이 논문은 2012년도 정부(교육과학기술부)의 재원으로 한국연구재단의 기초연구사업 지원을 받아 수행된 것임(No. 2012-0555)
References
-
M. Gad-el-Hak, "Modern developments in flow control", Appl. Mech, 49(7), p365, (1996).
[https://doi.org/10.1115/1.3101931]
-
T. Igarashi, "Drag reduction of a square prism by flow control using a small rod", Journal of Wind Engineering and Industrial Aerodynamics, 69-71, p141-153, (1997).
[https://doi.org/10.1016/S0167-6105(97)00150-5]
-
H. Sakamoto, K. Tan, N. Takeuchi, and H. Haniu, "Suppression of fluid forces acting on a square prism by passive control", Journal of Fluids Engineering, 119, p506-511, (1997).
[https://doi.org/10.1115/1.2819273]
-
T. Tamura, and T. Miyagi, "The effect of Turbulence on aerodynamic forces on a square cylinder with various corner shapes", Journal of Wind Engineering and Industrial Aerodynamics, 83, p135-145, (1999).
[https://doi.org/10.1016/S0167-6105(99)00067-7]
- W. C. Park, "Effect of the length of a splitter plate on drag reduction”, Transactions of the Korean Society of Mechanical Engineers B", 17(11), p2809-2815, (1993), (in Korean).
-
Con J. Doolan, "Flat-plate interaction with the near wake of a square cylinder", The American Institute of Aeronautics and Astronautics Journal, 47(2), p475-478, (2009).
[https://doi.org/10.2514/1.40503]
-
K. D. Ro, S. M. Yoon, D. H. Choi, J. H. Kim, and E. C. Sim, "Drag reduction on a square prism using a detached splitter plate”, Journal of the Korean Society of Marine Engineering, 36(6), p808-813, (2012), (in Korean).
[https://doi.org/10.5916/jkosme.2012.36.6.808]
- K. Kamemoto, "On attractive features of advanced vortex methods and their subjects as a tool of lagrangian large eddy simulation", Proceedings of the fourth International Conference on Hydrodynamics, p37-56, (2000).
-
K. D. Ro, Baoshan Zhu, and Hokeun Kang, "Numerical analysis of unsteady viscous flow through a weis-fogh type ship propulsion mechanism using the advanced vortex method”, Journal of Fluids Engineering, 128, p481-487, (2006).
[https://doi.org/10.1115/1.2174059]
- J. S. Uhlman, "An integral equation formulation of the equation of motion of an incompressible fluid", Technical Report 10-086, Naval Undersea Warfare Center, America, (1992).
-
B. E. Lee, "The effect of turbulence on the surface pressure field of a square prism”, Journal of Fluid Mechanics, 69(2), p263-282, (1975).
[https://doi.org/10.1017/S0022112075001437]