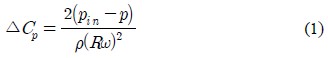The influence of guide vane opening on the internal flow of a francis turbine

1. Introduction

Francis turbine is the most widely used turbine in the world. It has a wide head range from 20m to 700m. And its connected generator output power varies from just a few kilowatts up to one gigawatt. Besides, the most important fact is that its efficiency can be as high as over 90%.

However, guide vanes operated at off-design point resulting into the unsteady flow remains a challenge to overcome. Many studies were conducted experimentally and computationally to reveal and solve the problem. Hasmatuchi et al. [1] experimentally pointed out that pressure fluctuation in the turbine has some relations to the guide vane channels and the large vaneless space between the runner and the guide vane at low opening. Khare et al. [2] also proved that the guide vane opening have large influence in the whirl velocity at runner outlet by CFD method. Muntean et al. [3][4] monitored the cavitation performance of a Francis turbine operated at nominal head and variable discharge and obtained the proper guide vane axis location by simulating the 3-D flow characteristics for the whole operating range. Alnaga et al. [5] developed an automatic iterative procedure for optimal design of distributors(including stay vane and guide vane) and successfully applied in a Francis turbine.

However, the influence of guide vane for a certain Francis turbine is hard to standardized. In order to examine the influence of the guide vane opening to the internal flow of a Francis turbine with specific speed of 80.5, a series of CFD analysis are conducted in this study. First, CFD analysis on the internal flow of a Francis turbine model for up to 9 guide vane angles is performed and an optimal guide vane angle is obtained. Secondly, CFD analysis on the turbine with guide vane number varying from 12 to 20 are conducted to get the ideal value. Finally, relations of the angle and number of guide vane with the performance of the turbine are examined using static pressure and circumferential velocity.

2. Turbine model

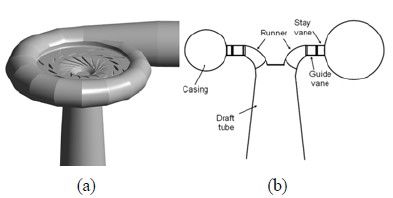
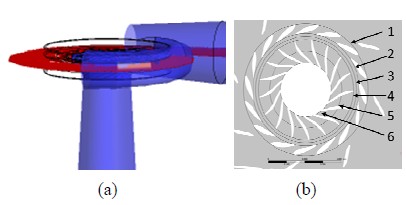
Figure 1 shows the schematic view of the Francis turbine model which is used for CFD analysis in this study. Figure 1 (a) shows the three dimensional view and Figure 1 (b) presents the two dimensional configuration of the turbine. The runner outlet diameter De is 0.350m. When the number of the blades is 17, the guide vane angle can be fully opened to 0.0694m(100%). The rotating speed of runner, effective head, output power and flow rate at the design point are N=900min^-1, H=60.73m, P=230kW and Q=0.46m³/s, respectively.

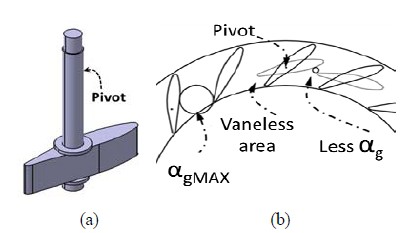
Figure 2 (a) shows the 3D modeling of the guide vane. The guide vane rotates to the pivot to change the guide vane angle α_g as shown in Figure 2 (b). Guide vane angle reaches its the maximum value of α_gMAX. When the tip of vane reaches the inlet of runner or inversely, it shows a less α_g. The area between guide vane and runner is defined as vaneless area.

Moreover, Tables 1 and 2 show the cases of CFD analysis by the variation of guide vane angle and guide vane number. CFD analysis on the influence of guide vane angle is firstly carried out with guide vane number is 16 and optimal guide vane angle is obtained. Then CFD analysis on the influence of guide vane number is secondly conducted based on the optimal guide vane angle.

3. Numerical Methods

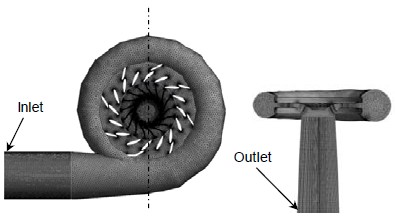
This study employs a commercial CFD code of ANSYS CFX [6] to conduct CFD analysis. As shown in Figure 3, tetrahedral numerical grids of about 19.8×10⁶ are adopted for the analysis of the calculation domain including inlet pipe, casing, runner and draft tube. Relatively dense grids are applied to the runner. Fine hexahedral numerical grids are employed for the draft tube of the turbine.

Figure 1:

(a) 3D view of Francis turbine model; (b) 2D view of Francis turbine model

Figure 2:

(a) Guide vane modeling with pivot; (b) Schematic view of guide vane angle(αg) variation

Table 1:

Cases of CFD analysis by guide vane angle

Table 2:

Cases of CFD analysis by guide vane number

Figure 3:

Numerical mesh of turbine model

Table 3:

Numerical methods and boundary condition

The numerical methods and boundary condition are set as shown in Table 3. Shear stress transport(SST) model is adopted as turbulence model because of its relatively good convergence in the complicated flow field of turbomachinery. The flow conditions are imposed at boundary conditions related to constant pressure estimated by ρgH at the inlet and averaged outflow at the outlet. At the interface between the rotating domain (runner) and stationary domain (guide vane & draft tube) a frozen-rotor interface is used. All calculations are conducted under the condition of steady state.

4. Results and Discussion

4.1 Performance curves

The flow field is investigated when guide vane openings (guide vane angle and guide vane number) are changed.

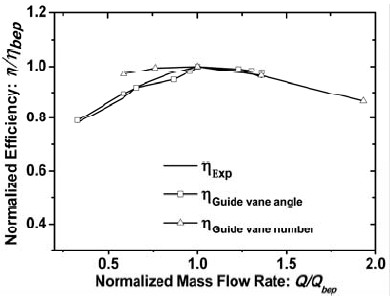
Figure 4 shows the performance curves of the Francis turbine model. The best efficiency point is taken as reference condition. As both guide vane angle and guide vane number are related to flow rate, flow rate ratios are considered to be the axis of abscissas and thus, the efficiency curves by two kinds of guide vane opening control methods can be easily compared. The axis of ordinates reveals normalized efficiency.

Figure 4:

Efficiency curves by guide vane opening

The efficiency curve η_EXP is referred to the turbine manufacturer's design data [7]. The present CFD analysis result of efficiency curve by guide vane angle presents a good convergence with the designed curve, which indicates that the adopted numerical method here is reliable.

Moreover, the CFD analysis result of efficiency curve by guide vane number shows a relatively better efficiency in partial load cases(Q/Q_bep is less than 1) but a little lower efficiency in excessive load cases in comparison with those by the results of guide vane angle control.

Compared with Tables 1 and 2, an optimal guide vane opening with guide vane angle opened to 38.9% and guide vane number equaled to 16 is obtained.

4.2 Pressure contours and velocity vectors by guide vane angle

Figure 5 shows the test plane and locations in the turbine. Figure 5 (a) shows the central plane for test pressure contours and velocity vectors because the data here are quite representative. Figure 5 (b) shows the six radial locations of pressure and velocity distributions on the plane. The inlet and outlet of guide vane, the vaneless area, the inlet, mid-radial and outlet of runner are noted as Locations 1 to 6.

Figure 5:

(a) Test plane of pressure contours and velocity vectors; (b) Radial locations of pressure and velocity on the plane shown in Figure 5 (a)

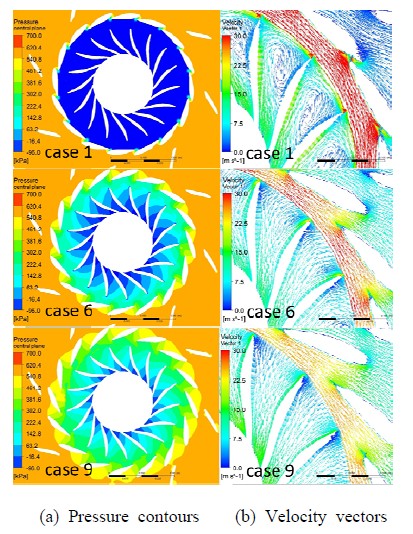
Static pressure contours and velocity vectors in the turbine by guide vane angle are shown in Figure 6. Case 1 is chosen as representative for its typical internal flow characteristic of partial load case which is quite different from that of Case 6. Case 6 is a case by the flow rate at the best efficiency point(bep) that is considered as normal criterion. Similarly, Case 9 is chosen to present the internal flow characteristics of Francis turbine in over load condition.

Figure 6( a) shows a sharp pressure transition along the guide vane passages and lower pressure in the runner in Case 1 by partial load. On the contrary, pressure decreases gradually when water passes through relatively wide guide vane passages in Case 6.

Velocity vectors in Figure 6 (b) are taken from the same passage of the runner in Figure 6 (a). Recirculation flow in the runner passage, which is shown as relative velocity vectors, and relatively high circumferential velocity, which is shown as absolute velocity vectors, in the vaneless area are observed in Case 1, which could be the reasons that the efficiency of Case 1 is quite lower than that of Case 6.

On the other hand, the velocity vectors in Case 9 show a quite uniform flow passing through the runner passage.

Figure 6:

Pressure contours and velocity vectors in the turbine by guide vane angle.

Figure 7:

Pressure distributions in the turbine at the design point (Case 6).

Figure 8:

Absolute circumferential velocity distributions in the turbine at the design point (Case 6).

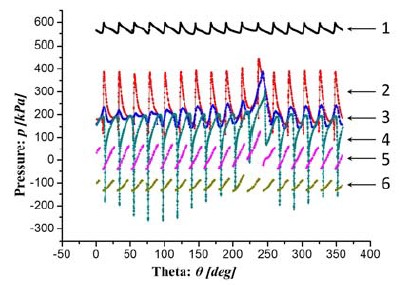
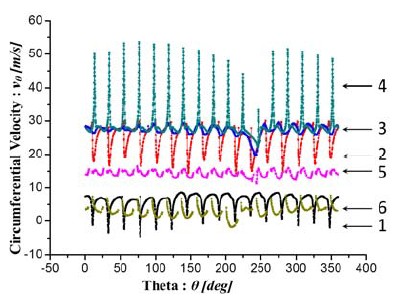
Figures 7 and 8 show the static pressure and absolute circumferential velocity distributions from Locations 1 to 6 at the designed flow rate range of Case 6. The test locations are shown in the Figure 5.

The pressure distributions at each location show gradual decrease of static pressure from Locations 1 to 6. The decreased static pressure changes to output torque in the runner passage.

Moreover, circumferential velocity distributions show that, from Locations 1 to 3, the velocity increases gradually due to the guided flow direction by the guide vane but decreases apparently from Locations 4 to 6, which means that the increased angular momentum in the regions from Locations 1 to 4 changes to output torque in the Locations 4 to 6.

Figure 9 shows the pressure distributions in the Francis turbine by the differential pressure coefficient:

where p_in is the static pressure at the inlet of turbine casing and p is the local static pressure of test location, R is the diameter of runner inlet, and ω is angular velocity.

Figure 9:

Averaged pressure distributions in the turbine by guide vane angle.

Figure 10:

Averaged circumferential velocity distributions in the turbine by guide vane angle.

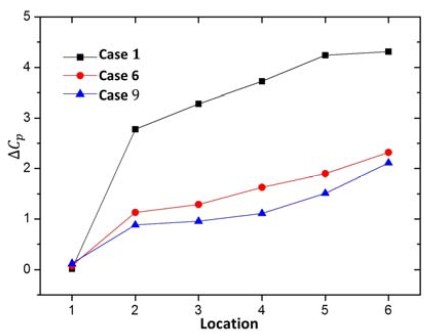
The difference of static pressure increases drastically between the Locations 1 and 2 in all case as shown in Figure 9, which implies that pressure decrease occurs considerably at the guide vane passage because of the increased circumferential velocity in the guide vane passage. Especially, in the Case 1, the amount of pressure decrease is considerably larger than those of the other cases. The larger amount of pressure decrease at the guide vane passage may lead to the low efficiency in the partial load ranges.

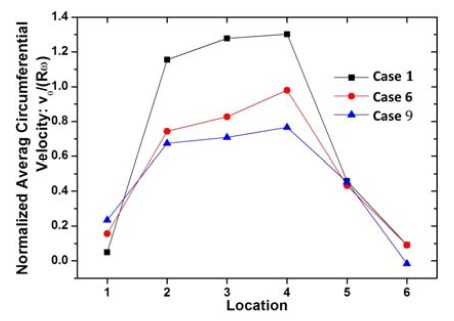
Figure 10 shows the averaged circumferential velocity distributions in those three cases. Case 1 shows relatively higher velocity from Locations 2 to 4 but decrease drastically from Locations 4 to 5, which means that there exists considerable hydraulic loss by recirculation flow in the runner passage as shown in Figure 6 (b).

4.3 Pressure contours and velocity vectors by guide vane number

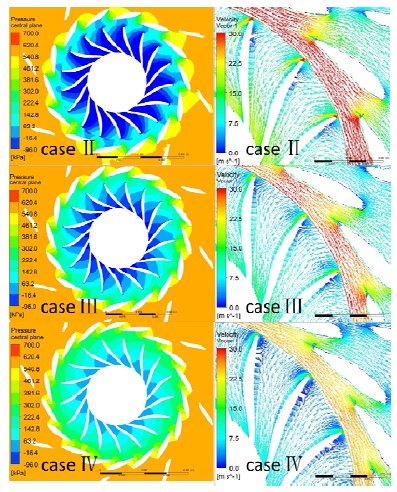
Corresponding to the flow rate in Case 1, Case 6 and Case 9, Case Ⅳ, Case Ⅲ and Case Ⅱ are chosen as typical cases to analyse to internal flow characteristics in the Francis turbine influenced by the guide vane number, respectively. Figure 11 shows the pressure contours and velocity vectors on the test plane shown in Figure 5 (a) by guide vane number. Unlike the cases by guide vane angle, the less of guide vane number is, the larger the guide vane opening will be. As the guide vane angle and inlet pressure are set to same value in all cases, and Case Ⅱ has the largest flow rate, static pressure at the runner passage in Case Ⅱ is lower than those of the other cases as shown in Figure 11 (a).

On the other hand, Unlike the velocity vectors of Case 1 in Figure 6 (b), there is no recirculation flow region in the runner passage even at the partial load condition in Case Ⅳ. Relatively higher guide vane angle in Case Ⅳ than that of Case 1 should have lead the main stream of the flow into the runner passage without the occurrence of recirculation flow.

Figure 12 shows the averaged pressure distributions by the differential pressure coefficient ΔC_p in the Francis turbine model according to the variation of guide vane number. Case Ⅱ shows relatively higher value of ΔC_p at all locations in comparison with those of Cases Ⅲ and Case Ⅳ. The tendency of pressure distribution in the turbine passage by the guide vane number is close to proportional to the flow rate by comparing the ΔC_p versus to test location curves of Case Ⅱ, Cases Ⅲ and Case Ⅳ.

Figure 11:

Pressure contours and velocity vectors in the turbine by guide vane number.

Figure 13 shows the averaged circumferential velocity distributions in the turbine by guide vane number. Due to the same guide vane angle, circumferential velocity at the Locations 1 to 4 shows almost same distribution pattern with the change of the velocity at each location according to the mass flow rate of the Cases Ⅱ to Ⅳ. And then, the circumferential velocity decrease abruptly from the Locations 4 to 6.

Figure 12:

Averaged pressure distributions in the turbine by guide vane number.

Figure 13:

Averaged circumferential velocity distributions in the turbine by guide vane number.

5. Conclusions

According to the investigation of the influence of guide vane opening, which includes the variation of angle and number of the guide vane, guide vane opening gives considerable influence to the internal flow and performance of the Francis turbine. The optimum guide vane opening is obtained at a guide vane angle of 38.9% and at a guide vane number16. Relatively larger variation of the pressure and velocity distributions is found by guide vane angle in comparison with that of guide vane number. Guide vane opening controlled by guide vane number shows a quite better efficiency in partial load condition than that by guide vane angle, other than almost equivalent efficiency in excessive load condition. More uniform flow in the turbine runner passage occurs in partial load cases by guide vane number. Therefore, in order to get a larger operating range, a possible way to is to control the mass flow rate with the guide vane number by keeping the guide vane angle.

Acknowledgments

This research was financially supported by the Ministry of Education, Science and Technology (MEST) and National Research Foundation of Korea(NRF) and Jeonnam Science & Technology Promotion Center (JNSP) through the research & development project of Jeonnam Science Park.

References

• V. Hasmatuchi, M. Farhat, P. Maruzewski, and F. Avellan, "Experimental investigation of a pump-turbine at off-design operating conditions", Proceedings of the 3rd International Association for Hydro-Environment Engineering and Research International Meeting of the Workgroup on Cavitation and Dynamic Problems in Hydraulic Machinery and Systems, (2009).
• R. Khare, V. Prasad, and S. Kumar, "CFD approach for flow characteristics of hydraulics Francis turbine", International Journal of Engineering Science and Technology, 2(8), p3824-3831, (2010).
• S. Muntean, R. F. Susan-Resiga, S. Bernad, and I. Anton, "Analysis of the GAMM Francis turbine distributor 3D flow for the whole operating range and optimization of the guide vane axis location", Proceedings of the 6th International Conference on Hydraulic Machinery and Hydrodynamics, p131-136, (2004).
• S. Muntean, I. Ninaci, R. Susan-Resiga, A. Baya, and I. Anton, "Numerical analysis of the flow in the old Francis runner in order to define the refurbishment strategy", University Politehnica of Bucharest Scientific Bulletin, Series D, 72(1), p117-124, (2010).
• A. Alnaga, and J. L. Kueny, "Optimal design of hydraulic turbine distributor", World Scientific and Engineering Academy and Society Transactions on Fluid Mechanics, 3(2), p175-185, (2008).
• ANSYS CFX Documentation, http://www.ansys.com, Accessed, May 20, 2012.
• Tanaka, Suiryoku, Technical Design Book of Francis Hydro Turbine, Japan, (2012).