Design of RCGA-based PID controller for two-input two-output system
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited
Abstract
Proportional-integral-derivative (PID) controllers are widely used in industrial sites. Most tuning methods for PID controllers use an empirical and experimental approach; thus, the experience and intuition of a designer greatly affect the tuning of the controller. The representative methods include the closed-loop tuning method of Ziegler-Nichols (Z-N), the C-C tuning method, and the Internal Model Control tuning method.
There has been considerable research on the tuning of PID controllers for single-input single-output systems but very little for multi-input multi-output systems. It is more difficult to design PID controllers for multi-input multi-output systems than for single- input single-output systems because there are interactive control loops that affect each other.
This paper presents a tuning method for the PID controller for a two-input two-output system. The proposed method uses a real- coded genetic algorithm (RCGA) as an optimization tool, which optimizes the PID controller parameters for minimizing the given objective function. Three types of objective functions are selected for the RCGA, and each PID controller parameter is determined accordingly. The performance of the proposed method is compared with that of the Z-N method, and the validity of the proposed method is examined.
Keywords:
Proportional-integral-derivative controller, TITO system, Real-coded genetic algorithm, Objective function1. Introduction
PID (proportional-integral-derivative) controllers are widely used in industrial sites. Most actual systems in industrial sites are multivariable systems wherein each output is affected by at least one of the inputs. Therefore, they have a complex structure, and are significantly affected by disturbances and noise. Accordingly, the process to design a PID controller for these systems is very complicated.
Most tuning methods for PID controllers have an empirical and experimental approach; thus, the experience and intuition of the designer greatly affect the tuning of the controller. The representative methods include the closed-loop tuning method of Ziegler-Nichols (Z-N), the Cohen-Coon (C-C) tuning method, and the Internal Model Control tuning method.
Niederlinski [1] suggested a PID-controller design method for a TITO (two-input two-output) system based on the generalized Z-N method. Skogestad [2], Chiu [3], Hovd [4], and Gagnon [5] suggested a robust decentralized controller designed using the μ-Synthesis theory. Um and Suh [6] suggested a decentralized LQ-PI controller tuning method for a TITO system for overcoming an extreme constraint where the number of state variables and the number of outputs are equal in the state-space equation for the system.
In this paper, a tuning method for the PID controller of a TITO system, which is a multivariable system, is investigated.
A series of processes that searches for the optimal parameters of the PID controller for the TITO system using a RCGA (real-coded genetic algorithm) is proposed. This method uses RCGA as an optimization tool, which optimizes the controller parameters for minimizing the given objective function. Three types of objective functions are selected for the RCGA, and each PID controller parameter is determined accordingly. By comparing the performance of the proposed method with that of the Z-N method, the validity of the proposed method is examined.
2. TITO System
2.1 Multi-variable system
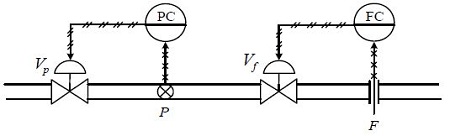
In many cases, control systems commonly found in industrial sites have to control more than two variables. Additionally, there can be interference in mutual outputs, as shown in Figure 1. Here, when the pressure (P) is controlled by operating the pressure control valve (Vp), the flow (F) within the pipe changes at the same time. When the flow is controlled by operating the flow control valve (Vf), the flow within the pipe changes along with the pressure. That is, under the condition that the flow is consistent with a target value while the pressure differs from a target value, when is operated to adjust the pressure, the flow—which has the correct value—is inevitably changed. A similar situation occurs for the pressure when is operated to adjust the flow.
2.2 TITO System
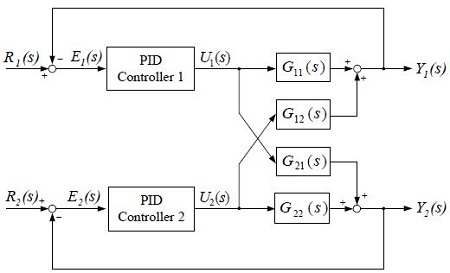
In this paper, a TITO system, which is one of the most common multivariable systems, is examined. As shown in Figure 2, a TITO system comprises two inputs and two outputs.
As shown in the figure, the TITO system is divided into the transfer functions G11(s), G12(s), G21(s), and G22(s) and G12(s) and G21(s) induce mutual interference in their outputs.
R(s)∈R2 is the reference input, E(s)∈R2 is the error, U(s)∈R2 is the control input, and Y(s)∈R2 is the output vector.
The transfer function matrix G(s)of this TITO system is expressed by Equation (1).
| (1) |
As shown in Figure 2, each control input is determined by the PID controller using each error variable. This can be expressed in a diagonal matrix PID controller format excluding the transfer matrix, as shown in Equation (2).
| (2) |
and represent the controllers PID1 and PID2, respectively.
To obtain each gain matrix, Equation (2) can be modified into Equation (3).
| (3) |
where Kp∈R2×2 is the proportional gain matrix, Ki∈R2×2 is the integral gain matrix, and Kd∈R2×2 is the derivative gain matrix. They can be expressed as follows.
| (4) |
3. PID Controller of the TITO System
3.1 PID controller based on Z-N
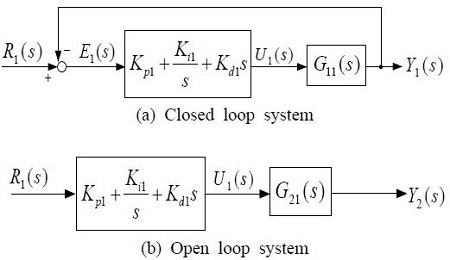
In the TITO system, the outputs of the two controllers have a mutual effect on each other; thus, the tuning rule of Z-N can not be directly applied to a single-input single-output (SISO) system. Thus, it is necessary to divide a TITO system into two SISO systems. When the control input U(s) in Figure 2 is set as ‘0’ in order to design a PID1 controller, it can be divided into two SISO systems for the input R1(s), as shown in Figure 3. In this regard, one SISO system becomes a closed-loop system, as shown in Figure 3 (a), and the other becomes an open-loop system, as shown in Figure 3 (b).
In Figure 3 (b), the input U1(s) can be considered as a disturbance or sensor noise added to the output Y2(s), and this does not affect the error E1(s) necessary for the controller design. Thus, to design a PID1 controller for the reference input R1(s), only Figure 3 (a) must be considered.
On the other hand, to design a PID2 controller, the control variable U1(s) must be removed. Then, the system in Figure 2 can be divided into two SISO systems for the input R2(s), similarly to Figure 3. Here, one SISO system becomes a closed-loop system, and the other becomes an open-loop system.
The Z-N tuning formulas for the PI and PID controllers are shown in Table 1. We considered only the PID controller.
3.2 PID controller based on RCGA
In this section, an RCGA used to resolve an optimization problem that occurs during the design of PID controllers is briefly examined [7].
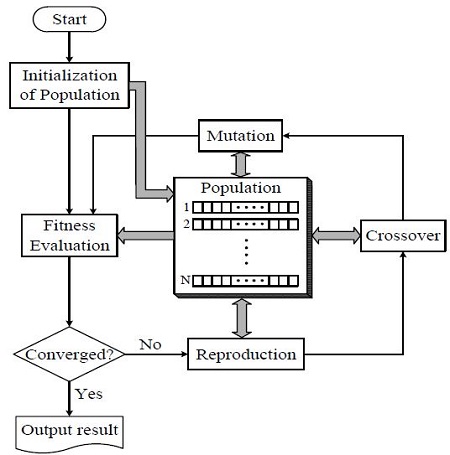
An RCGA is an algorithm based on natural selection and genetics. It starts from an initial group that consists of a number of individuals (chromosomes) and a group that has been newly formed through fitness evaluation. A genetic operator repeatedly performs simulated evolution until an optimal solution is found. Figure 4 shows the operation process of the RCGA employed in this paper.
For the genetic operator used in the RCGA, reproduction similar to the gradient, a modified simple crossover, and dynamic mutation are used. A scaling-window method is used to increase the selection pressure, and an elite strategy is used to guarantee that the strongest individual is passed onto the next generation by preventing the optimal individual extinction of a generation.
Regarding the objective function necessary to determine the PID V controller parameters according to the RCGA, three kinds of objective functions are applied, as previously mentioned.
The objective functions used to determine the parameters of the PID controller are the ISE (Integral of squared error) shown in Equation (5), which can obtain a global solution even in a search environment with multi-modal characteristics and can easily obtain a derivative; the IAE (Integral of absolute error) shown in Equation (6) and the ITAE (Integral of time-absolute error) shown in Equation (7).
| (5) |
| (6) |
| (7) |
The ISE is frequently used for optimally designing controllers owing to its ease of interpretation but gives a large offset when the error is large and a small offset when the error is small. Thus, it is insensitive to the change in the coefficient near an optimal solution. On the other hand, the IAE assigns an equal offset for the positive or negative error by considering the absolute magnitude of the error and has better sensitivity than the ISE. The ITAE is a very useful criterion that gives an offset for a long-term transient phenomenon. It has far more discriminating power than the IAE and ISE, and the minimum value of this integral can be better defined when the parameters of the system change [8].
4. Simulation
4.1 System and controller design
To examine the validity of the proposed method, a linearized TITO system [1] is considered, as shown in Equation (8). This system is not a typical process-control problem, as the plant is not diagonally dominant and also has one large and negative diagonal gain.
| (8) |
When the closed-loop transfer function is obtained by setting the critical proportional gain Kcr for G11(s) , it is expressed by Equation (9).
| (9) |
The Kcr value of the stability limit where an output induces oscillation with a constant amplitude can be obtained by the Routh–Hurwitz stability criterion.
In this case, the value is Kcr=9. When the period of oscillation Pcr is calculated by determining the oscillation frequency using the characteristic equation in Equation (9), it is 0.56 sec. Therefore, the parameters of the PID controller according to the Z-N tuning rule (refer to Table 1) are determined as follows: Kp1 = Kp2 = 5.4, Tp1 = Tp1 = 0.28 and Td1 = Td2 = 0.07.
For the control variables of the RCGA, the population size N = 20, reproduction coefficient η = 1.8, crossover probability Pc = 0.9, and mutation probability Pm = 0.2 are used. The upper boundary values of the PID controller parameters , , and are set to 25, including a sufficient margin based on the PID controller parameters obtained by the Z-N method. By decreasing the search range of RCGA, the computation time is reduced, and a global solution is guaranteed.
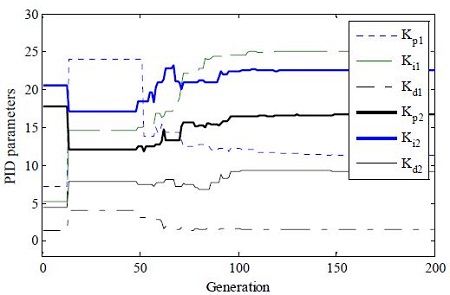
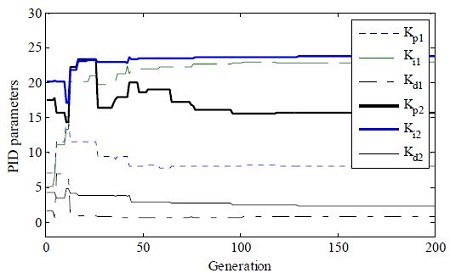
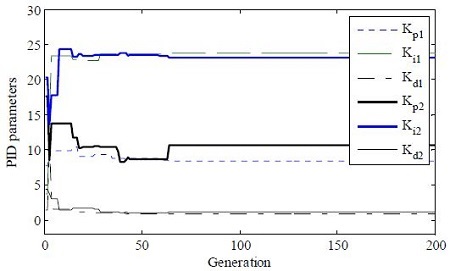
The parameters of the PID controller are determined by using the ISE, IAE, and ITAE as objective functions of the RCGA. Figure 5–7 show the determination of the PID controller parameters by using the ISE, IAE, and ITAE.
| (10) |
| (11) |
| (12) |
where tf is a time that is sufficiently large that the integral after this time can be ignored.
Table 2 summarizes the PID controller parameters based on Z-N and the RCGA
4.2 Performance comparison
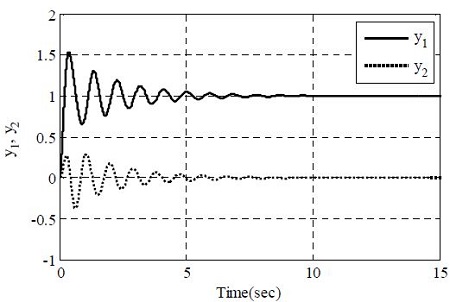
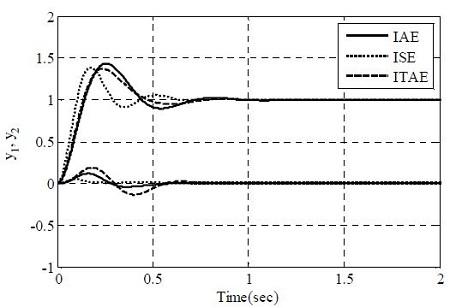
To examine the validity of the proposed method, a stepwise set-point tracking experiment is conducted. The target value r(t) = [1 0]T is applied to each controller, and the output y(t) = [y1(t) y2(t)]T is examined. Figure 8–9 show the responses of the PID control systems tuned by the Z-N method and the proposed method. As shown, both the responses of the Z-N method and the proposed method reach the set point, but the response of the Z-N method oscillate excessively, with a large overshoot and a long settling time.
Table 3 shows the percentage overshoot (Mp), rising time (tr), and 2% settling time (ts) for a quantitative comparison of the performance of each method. Here, tr = t90 - t10 is used, where t10 and t90 are the times taken for the output to reach 10% and 90%, respectively, of the set point. As summarized in the table, the control performances of the PID control systems based on the RCGA are superior to those for the Z-N method in every aspect.
5. Conclusion
Generally, in a multivariable system, more than two variables must be controlled. These systems are typically complicated, as the mutual outputs induce interference in each other.
In this paper, a method to determine the optimal parameters of a PID controller using an RCGA for a TITO system, i.e., a multivariable system, was proposed. Three kinds of objective functions were selected for the RCGA—the ISE, IAE, and ITAE—and the PID controller parameters for each case were determined independently. The response characteristic varied according to the objective function; thus, we considered that they can be usefully applied depending on the system and control environment.
To verify the validity of the proposed method, the performances were compared with the Z-N tuning method using a computer simulation. The response of the Z-N tuning method oscillated excessively, exhibited a large overshoot, and took a relatively long time to stabilize. The PID control system based on the RCGA exhibited superior performances compared with the Z-N tuning method with regard to control performance indices such as the overshoot, rise time, and settling time.
Acknowledgments
This paper is based on the improvement of the M.S. Thesis “Design of PID Controller for TITO system using RCGA” (Department of Mechatronics, Graduate School, Korea Maritime and Ocean University).
References
-
A. Niederlinski, “A heuristic approach to the design of linear multivariable interating control system”, Automatica, 7(6), p691-701, (1971).
[https://doi.org/10.1016/0005-1098(71)90007-0]

-
S. Skogestad, and M. Morari, “Robust performance of decentralized control systems by independent designs”, Automatica, 25(1), p119-125, (1989).
[https://doi.org/10.1016/0005-1098(89)90127-1]

-
M. Chiuand, and Y. Arkun, “A methodology for sequential design of robust decentralized control systems”, Automatica, 28(5), p997-1001, (1992).
[https://doi.org/10.1016/0005-1098(92)90153-7]

-
M. Hovd, and S. Skogestad, “Sequential design of decentralized controllers”, Automatica, 30(10), p1601-1607, (1994).
[https://doi.org/10.1016/0005-1098(94)90099-X]

-
E. Gagnon, A. Pomerleau, and A. Desbiens, “Mu-synthesis of robust decentralized PI controllers”, IEE. Proceedings of Control Theory Application, 146(4), p289-294, (1999).
[https://doi.org/10.1049/ip-cta:19990324]

- T. H. Um, and B. S. Suh, “A LQ-PI controller tuning for TITO system”, The Institute of Electronics Engineers of Korea, 41(5), p275-280, (2004).
- G. G. Jin, Genetic Algorithms and Their Application, Kyowoosa, (2004).
- D. E. Kim, and G. G. Jin, “Model-based tuning rules of the PID controller using real-coded genetic algorithms”, Journal of Institute of Control, Robotics and Systems, 8(12), p1056-1060, (2002).