Non-contact monitoring of 3-dimensional vibrations of bodies using a neural network
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited
Abstract
Gas piping systems in power plants and factories are always influenced by the mechanical vibrations of rotational machines such as pumps, blowers, and compressors. Unusual vibrations in a gas piping system influence possible leakages of liquids or gases, which can lead to large explosive accidents. Real-time measurements of unusual vibrations in piping systems in situ prohibit them from being possible leakages owing to the repeated fatigue of vibrations. In this paper, a non-contact 3-dimensional measurement system that can detect the vibrations of a solid body and monitor its vibrational modes is introduced. To detect the displacements of a body, a stereoscopic camera system is used, through which the major vibration types of solid bodies (such as X-axis-major, Y-axis-major, and Z-axis-major vibrations) can be monitored. In order to judge the vibration types, an artificial neural network is used. The measurement system consists of a host computer, stereoscopic camera system (two-camera system, high-speed high-resolution camera), and a measurement target. Through practical application on a flat plate, the measured data from the non-contact measurement system showed good agreement with those from the original vibration mode produced by an accelerator.
Keywords:
Piping system, Non-contact, 3-dimensional measurement, Solid vibrations, Artificial neural network, Accelerator1. Introduction
Pneumatic and hydraulic piping lines control machinery such as the engines for ship propulsion and the engines for power plants. Abnormal vibrations from this machinery produces leakages in their piping systems, and eventually produce large accidents in the engines when the control pipe lines malfunction [1][2].
As one of the non-contact approaches for vibration measurements of machines or pipes, Machida et al. used laser speckle images to obtain the vibrational information of a machine. This method needs expensive laser sources to generate clear speckle patterns, and also requires complicated image analyses [3]. Yamagishi et al. measured flow-structure interactions of a flat plate vibrating in water [4].
This study is restricted to two-dimensional measurements of the vibrations of the plate. Jeon et al. [2][5] proposed a new measurement technique in which one high-speed camera was used and its time consecutive images were used to detect the displacement of measurement bodies. These results were also restricted to two-dimensional vibrations. Since most cases of solid vibrations are three-dimensional, it is necessary to measure the vibrations in three dimensions.
In this study, a non-contact three-dimensional measurement system for the detection of vibrations of solid bodies is newly proposed. Further, this study uses a monitoring system that can sort the solid vibrations into major vibration types by the use of an artificial neural network [6].
2. Monitoring Procedure
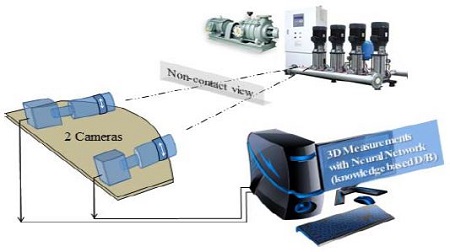
Figure 1 shows the schematics of the monitoring system for the machine vibrations. The main purpose of the measurement system is to detect the vibrations of piping system or machinery. Two high-speed high-resolution cameras are installed toward to the measurement target.
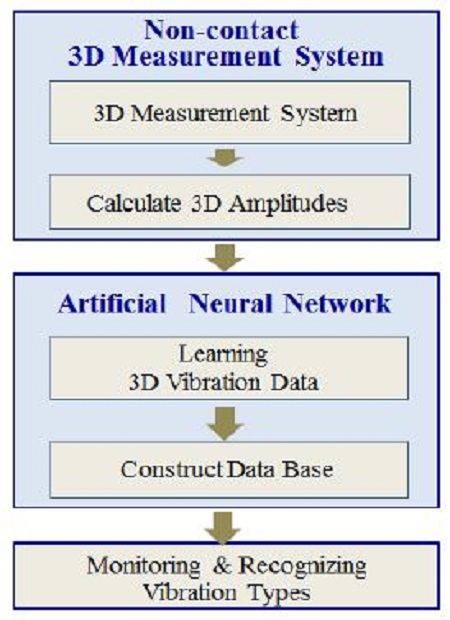
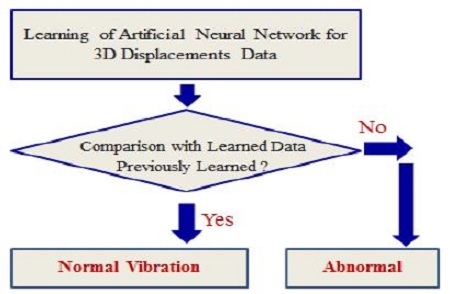
Figure 2 shows the decision-making procedure to clarify the vibration types of solid bodies. experimental setup. First, the displacements of the target body given by the machine vibration are calculated by the non-contact three-dimensional measurement system. Next, the displacement data are used for teaching the artificial neural network. Last, real-time monitoring of the vibrational machine is conducted based on the database that was learned in the teaching process of the artificial neural network.
3. Non-Contact 3D Measurements
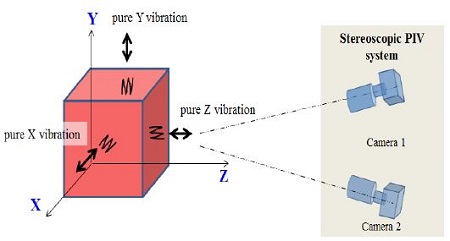
The non-contact three-dimensional measurement system for vibration consists of two cameras (high-speed high-resolution, 500 fps, 1024 × 1024 pixels), a host computer, and a halogen light. Figure 3 and 4 show the camera configuration for the measurement target.
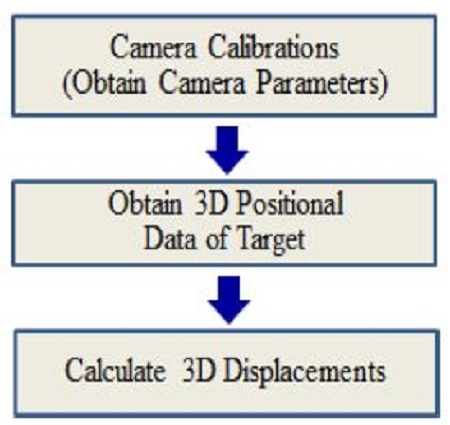
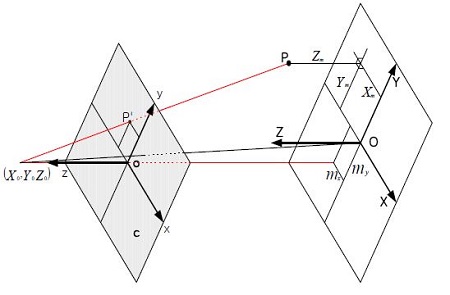
Figure 5 shows the procedure to obtain 3D displacements of the vibrational body. In order to perform 3D measurements with two cameras, a camera calibration process in which all camera parameters are calculated should be carried out before measurements. Two cameras were used to obtain the stereoscopic 3D measurements. The entire process, from camera calibration to the calculations of three-dimensional displacements of the body, is based on previous papers by Doh et. al [7]-[9]. Following is the brief procedure for camera calibration and 3D calculations. For camera calibration, a 10-parameter method was used. Ten unknown parameters (6 exterior parameters: l, α, β, γ, mx, my, and 4 interior parameters: cx, cy, k1, k2) are calculated in the calibration process. For camera calibration, the landmark shown in Figure 7 was used.
| (1) |
The calibration method is based on the pin-hole model. Equation (1) was used to construct the relation between the camera coordinates and the land coordinates (called absolute coordinates or physical coordinates). Here, cx and cy are the focal distances for the x and y components of the coordinates. Δx and Δy are the lens distortions. l refers to the distance between the origin O (0, 0, 0) and the principal point (X0, Y0, Z0) of the camera. (x, y) represents the camera (photographical) coordinates of the image centroid of the calibration targets. Xm, Ym, and Zm represent three-dimensional coordinates of the target (object) in the physical coordinates (land coordinates). mx and my are misalignments between the coordinate centers of the two coordinates. After camera parameters were calculated, the three-dimensional coordinates (X, Y, Z) of the vector were calculated using Equation (2). The rotational transformation matrix, MM, consists of the 10 camera parameters. That is, Equation (2), which represents the 3D position of the target, can be replaced with Equation (3).
| (2) |
| (3) |
ai,j(i = 1, 2, 3, j = 1, 2, 3) are the elements of the rotation matrix obtained via the camera calibrations. The final three-dimensional position of the target was calculated using Equation (4) below:
| (4) |
where (X1, Y1, Z1) and (X2, Y2, Z2) denote the absolute coordinates for camera 1 and camera 2, respectively, given by Equation (3).
Time-consecutive images of the two cameras were captured, and these images were used to calculate the 3D displacements of the same target. The principle of finding the same target in the time domain is based on the bidirectional method proposed by Doh et al. [9].
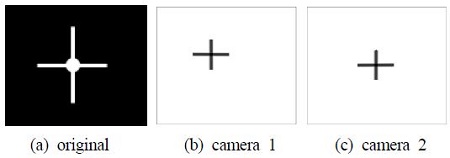
To check the performance of the constructed 3D measurement algorithm, a target as shown in Figure 8 (a) was attached to the wall of the object in Figure 3, 8 (b) and 8 (c) show the camera images reconstructed by the two cameras’ parameters. All camera parameters were obtained from the aforementioned calibration process. Using these parameters, artificial 3D data of the target vibrations were converted into 2D camera coordinates, and once again, the 3D displacements of the target vibration were recovered.
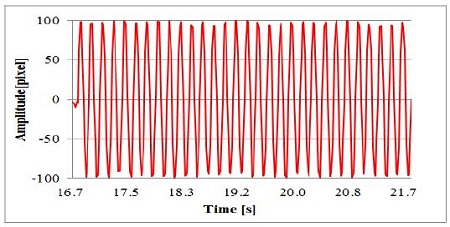
To generate the 2D artificial images shown in Figure 8 (b) and Figure 8 (c) were used. To generate the artificial images, the method used by Hwang [10] and Okamoto et al. [11] was adapted. Figure 9 shows the calculated 3D displacement data of the target vibration with time changes. The amplitude implies a nondimensional value in the pixels. In this study, these values were enlarged by 100 times. Therefore, the maximum actual amplitude is 1 mm. Figure 10 shows enlarged data in a range of time from 15 msec to 25 sec. As seen in this figure, X-direction vibration is clearly shown.
Order of vibrations with 10% noise of the maximum amplitude for time change [msec] (X-axis vibration→Y-axis vibration→Z-axis vibration) (unit: mm × 10-2, max amplitude=100)
Order of vibrations with 10% noise of the maximum amplitude for time change [msec] (X vibration→Y vibration→Z vibration) (unit: mm × 10-2, max amplitude=100)
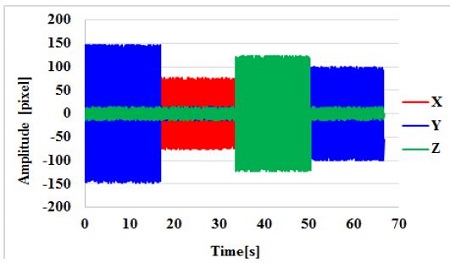
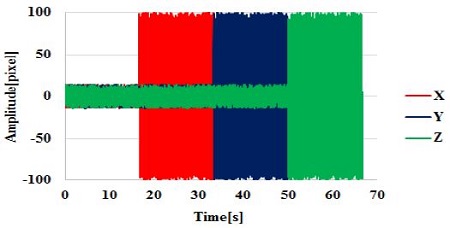
Figure 11 shows the calculated 3D displacement data for the vibrations. A time-consecutive vibration was determined in the order of Y-axis vibration, X-axis vibration, Z-axis vibration, and Y-axis vibration. These vibration data (i.e., displacements of the target) were trained by the artificial neural network explained in the next section.
4. Artificial Neural Network for Decision Making on Vibration Types
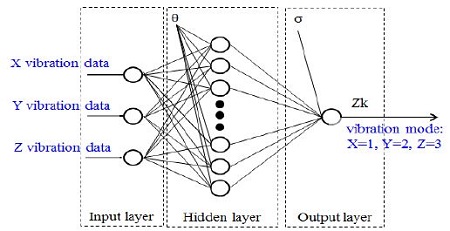
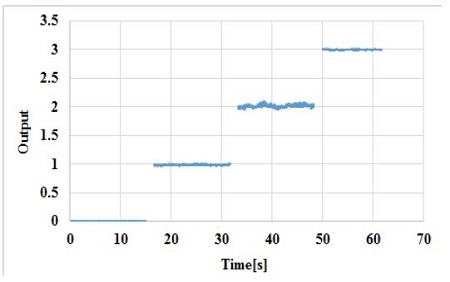
Figure 12 shows how the artificial neural network learns the 3D vibration data (displacement data), and how the decision- making is preformed. Once the neural network learned the normal vibrational data, the decision-making was straightforward. Known information on the vibrations was taught as 1, 2, and 3. That is, pure X-axis vibration was taught as X = 1, pure Y-axis vibration as Y = 2, and pure Z-axis vibration as Z = 3. Figure 13 shows the neural network used in this study. The network consists of three layers: input, hidden, and output. The number of input layers is 3.
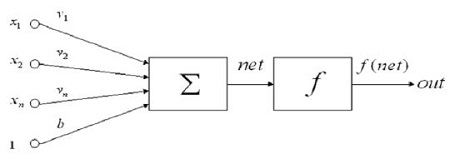
For each input, X-axis, Y-axis, and Z-axis vibration data were taught, as shown in Figure 13. The number of hidden layers is 10. The calculation algorithm of the neural network is based on the back-propagation used by the studies [2][5][12]. The calculation was repeated until the error value (E) between tk (teaching value) and zk (reference value) became smaller than a threshold value. Briefly mentioning on the calculation process for the neural network, the signal of each neuron can be represented as Equation (5) for the basic neuron model in Figure 14.
| (5) |
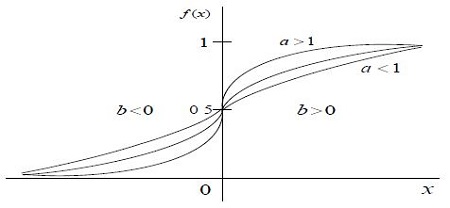
The signal of each neuron was regarded as following the sigmoid function as Equation (6).
| (6) |
Here, a and b are integers obtained in the process of calculating the neural network. To minimize the training error, offset values were used.
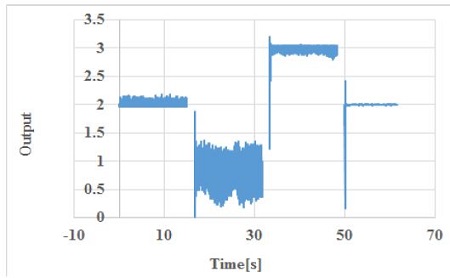
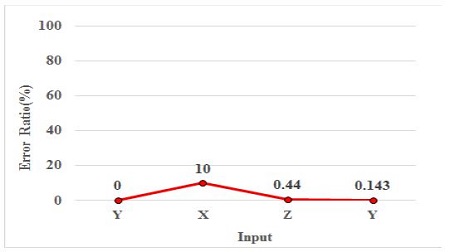
Figure 16 shows the results of decisions made by the constructed neural network. For the case of X-axis → Y-axis → Z-axis vibrations with a maximum amplitude of 100, decisions were clearly recovered to X = 1, Y = 2, and Z = 3, respectively, the same values of learning. Figure 17 shows the results of decisions made for the case of Y-axis (max amplitude: 150) → X-axis (max amplitude: 75) → Z-axis (max amplitude: 125) → Y-axis (max amplitude: 100) vibrations. There are some noisy decisions for Z-axis vibrations. This is because the S/N ratios of the X values are smaller than the vibrations of other axes. Figure 18 shows the error ratio of the decision-making. The error ratio was lower than 1% except in the case of the X-axis vibration. This value implies a failure percentage in deciding and judging the correct vibration type.
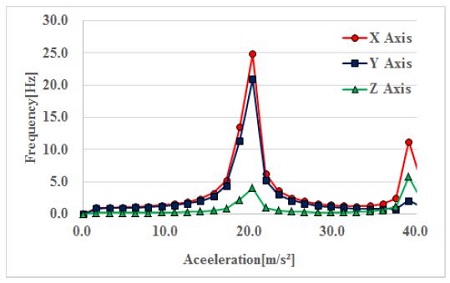
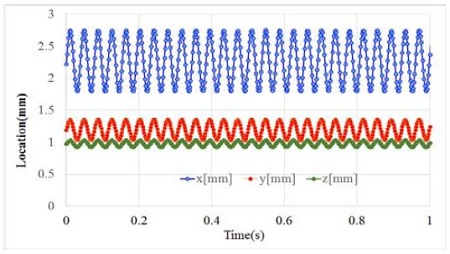
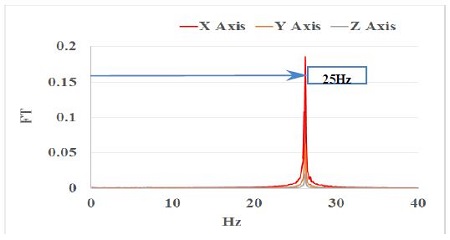
Figure 19 shows the frequency of an accelerator by which the target body in Figure 4 was forced to vibration. The frequency of the major vibration for the X, Y, and Z axes was 25 Hz. Figure 20 shows the measurement 3D results obtained by the constructed measurement system. Figure 21 shows the FFT results calculated from the 3D results in Figure 20. The frequency was 26 Hz. This value is 1 Hz different compared with that of the original accelerator’s frequency, showing the capability of the constructed measurement system.
6. Summary
A non-contact 3D measurement system for detecting solid vibrations was constructed using a stereoscopic camera system. When the S/N (signal-to-noise) ratio was large, the neural network failed in finding the correct vibration type with 10% of failure. The measurement system was validated via an acceleration test in which the measured frequency showed good agreement with that of the accelerator.
The measurement uncertainty for the displacement was lower than 5% for the entire measurement length.
Acknowledgments
The research was financially supported by the Basic Science Research Program (2014R1A1A4A01005191) and by the Human Resource Training Project for Regional Innovation (No.2015H1C1A1035890) through the National Research Foundation of Korea (NRF) funded by Ministry of Education, Science Technology.
References
- D. H. Doh, M. G. Jeon, J. H. Eum, and K. S. Kim, “Non-contact remote detection system for the failures of hydraulic and pneumatic systems”, Proceedings of the Korean Society of Marine Engineering, Annual Meeting, p111, (2012), (in Korean).
-
M. G. Jeon, G. R. Cho, J. S. Oh, C. J. Lee, and D. H. Doh, “Measurements of remote micro displacements of the piping system and a real time diagnosis on their working states using a PIV and a neural network”, Transactions of the Korean Hydrogen and New Energy Society, 24(3), p264-274, (2014), (in Korean).
[https://doi.org/10.7316/KHNES.2013.24.3.264]

- K. Machida, H. Okamura, T. Hirano, and K. Usui, “Stress analysis of mixed-mode crack of homogeneous and dissimilar materials by speckle photography”, Transactions of the Japan Society of Material Engineers, 67(655), p86-91, (2001).
- M. Shibahara, K. Yamaguchi, K. Masaoka, and T. Tsubogod, “Development of non-contact measurement for deformation and stress by image processing”, Proceedings of the Welding Structures Symposium, (2006).
-
M. G. Jeon, D. H. Doh, U. K. Kim, and K. K. Kim, “Evaluation on performances of a real-time microscopic and telescopic monitoring system for diagnoses of vibratory bodies”, Journal of the Korean Society of Marine Engineering, 38(10), p1275-1280, (2014).
[https://doi.org/10.5916/jkosme.2014.38.10.1275]

-
D. E. Rumelhart, G. E. Hinton, and R. J. Williams, “Learning representations by back-propagating errors”, Nature, p323-333, (1986).
[https://doi.org/10.1038/323533a0]

-
D. H. Doh, T. G. Hwang, and T. Saga, “3D-PTV measurements of the wake of a sphere”, Measurement Science and Technology, 15, p1059-1066, (2004).
[https://doi.org/10.1088/0957-0233/15/6/004]

-
T. S. Baek, and D. H. Doh, “Turbulent properties in a mixed statistically stationary flow”, Journal of the Korean Society of Marine Engineering, 37(7), p291-299, (2013).
[https://doi.org/10.5916/jkosme.2013.37.7.729]

- D. H. Doh, H. J. Jo, J. W. Sang, T. G. Hwang, Y. B. Cho, and Y. B. Pyeon, “A study on the development of a three-dimensional measurement system for flow-structure interaction using digital image processing”, Journal of Ocean Engineering and Tech, 18(4), p1-7, (2004).
-
T. G. Hwang, and D. H. Doh, “Performance test on 2D PIV and 3D PIV using standard images”, Korean Society of Mechanical Engineers (B), 28(11), p1315-1321, (2004).
[https://doi.org/10.3795/KSME-B.2004.28.11.1315]

-
K. Okamoto, S. Nishio, T. Saga, and T. Kobayashi, “Standard images for particle image velocimetry”, Measurement Science and Technology, 11(6), p685-691, (2000).
[https://doi.org/10.1088/0957-0233/11/6/311]

- D. H. Doh, T. Kobayashi, and T. Saga, “A color- to-temperature calibration method for thermo-sensitive liquid crystal using a neural network”, SEISAN-KENKYU, Institute of Industrial Science and Tech. Univ. of Tokyo, 47(4), p30-32, (1995).