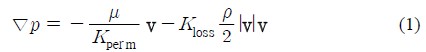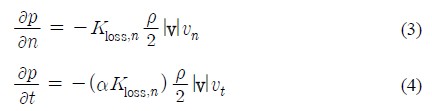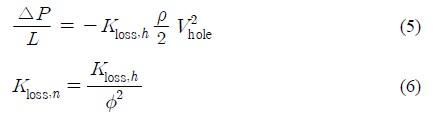Porous modeling for the prediction of pressure drop through a perforated strainer

1. 서 론

선박 및 플랜트에 사용되는 산업용 스트레이너(industrial strainer)는 해수 또는 청수가 유입되는 펌프의 전단부에 설치되어 불순물 유입을 방지하여 내부 기관의 안전운전을 보장하는 대표적인 기자재 중 하나이다. 스트레이너는 기본적으로 외면을 둘러싸는 몸체(body)와 내부에 이물질을 여과해 주는 필터(filter)로 구성된다. 필터는 작동유체 내 이물질을 걸러주기 위한 목적으로 사용 되는데, 외부의 필터는 일반적으로 판금(sheet metal)을 가공해 사용한다.

스트레이너는 유동시스템을 보호하기 위하여 사용하지만, 유체역학적 측면에서는 시스템 내 관로를 작동유체가 흐를 때 압력강하를 일으키는 하나의 저항체로 고려된다. 따라서 스트레이너의 경우에는 이물질을 설계기준까지 걸러내면서 보다 작은 압력강하(pressure drop)를 일으키게 하여 시스템의 전체 효율을 높이는 설계가 반드시 필요하다. 하지만 산업 현장에서는 스트레이너 설계를 위한 압력 강하량 예측은 주로 경험식 또는 실험식에 의존하고 있으며, 특히 대형 스트레이너의 경우에는 실험설비를 구비하기가 어렵기 때문에 대용량 컴퓨터를 이용한 유동해석을 활용하고 있는 추세이다.

최근 대부분의 스트레이너들은 많은 구멍(holes)과 구부림(bending)을 수반하는 등 필터의 형상이 매우 복잡하다. 이러한 스트레이너를 지나면서 발생하는 압력 강하량을 수치적으로 구하기 위해서는 원형 또는 직접 수치모사(prototype or direct numer-ical simulations)가 필요하나 이는 너무 높은 계산비용 때문에 수행하기가 매우 어렵거나 거의 불가능하다. 따라서 복잡한 형상을 가지는 스트레이너의 경우 원형 수치모사 대신 필터의 일부 또는 전체 영역을 다공성 매질(porous media)로 대체하여 해석하는 등 모델링 기법을 사용하는 것이 가장 경제적인 방법이라 할 수 있다.

지금까지의 연구를 살펴보면 타공형 스트레이너를 지나는 유동에 대한 직접적인 연구는 문헌에서 거의 찾을 수 없다. 아주 최근에서야 Guo et al. [1]이 타공판 유동에서 유동구조와 압력강하의 원인을 찾기 위하여 직접수치모사를 이용하여 연구한 바 있다. 그들의 연구에 의하면 레이놀주 수(Reynolds number), 공극율(porosity), 구멍 직경, 판 두께, 표면 거칠기(surface roughness) 그리고 판 경사각(plate inclination angle) 등이 압력강하에 일정하게 영향을 미치는 것으로 밝혀졌다. 그렇지만 그들은 직접수치모사의 높은 비용 때문에 단 하나의 구멍만이 존재하는 경우(반복형상)를 해석하였기 때문에 그들의 연구를 스트레이너 전체형상에 적용하기는 매우 어렵다. 본 논문에서는 스트레이너 안에 내장되어 있는 필터나 타공판(perforated plates)의 전부 또는 일부를 다공성 매질로 가정하고 Forchheimer 법칙을 채택하여 산업용 스트레이너를 지나는 유동의 압력 강하량을 정확히 예측하는 다공성모델링 기법을 적용하여 그 유효성을 확인하였다. 지금까지 다공성 매질을 지나는 유동에 대한 연구는 많이 이루어졌으나[2]-[10], 이를 타공형 스트레이너(perforated-type strainer)에 직접 적용한 연구는 문헌에서 거의 찾을 수 없다. 일반적으로 타공판은 구멍이 판의 수직방향(normal direction)으로 뚫려있기 때문에 수직방향과 횡방향(transverse direction)은 서로 다른 유동손실 특성을 가지고 있다. 따라서 Forchheimer 법칙을 적용할 때 두 가지 종류의 서로 다른 손실계수가 필요하며, 이 때문에 방향에 따라 서로 다른 손실계수를 부과하는 방향성손실 모델(directional loss model)을 적용해야만 한다. 본 논문에서는 앞서 설명한 바와 같이 타공판을 기준으로 수직방향과 횡방향 손실계수(loss coefficients)가 필요한데, 이러한 손실계수들을 수치적으로 간단히 구하는 방법을 역시 설명한다. 끝으로 적용된 다공성모델링 기법을 검증하기 위하여 스트레이너 전체형상에 대하여 원형 수치모사와 다공성모델 수치모사를 각각 수행하였으며, 얻어진 수치모사 결과들을 서로 비교한다.

2. 다공성모델링 기법

본 논문에서 적용된 다공성모델링 기법에 대하여 자세히 설명한다.

2.1 Forchheimer 법칙

다공성 매질을 지나는 유동을 수치적으로 해석하기 위해서는 추가적인 압력 생성항이 필요하며, 주로 다음과 같은 법칙을 사용한다[4]-[8][10][11].

여기서 p와 v는 각각 유동의 압력과 속도를, μ와 ρ는 각각 작동유체의 점성계수(dynamic viscosity)와 밀도(density)를, 그리고 K_perm와 K_loss는 각각 다공성 매질의 투과율(permeability)과 손실계수(loss coefficient)를 가리킨다. 식 (1)에서 전자는 점성에 의한 압력강하로서 Darcy 법칙(Darcy law)이라 불리며, 후자는 관성(inertia)에 의한 압력강하로서 Forchheimer 법칙(Forchheimer law)이라 불린다. Darcy 법칙은 매우 느린 유동(slow or creeping flows)에서만 타당하다고 알려져 있으며, 유동속도가 증가하면 관성효과가 커지게 되어 Forchheimer 법칙이 보다 타당해진다. 이때 손실계수 K_loss는 경험식이나 실험식을 포함하여 적절한 방법에 의해 결정되어져야 한다.

Figure 1:

Schematic illustrating the prototype and porous model for the numerical simulation on a strainer

본 논문에서 다루는 스트레이너의 입구 유동속도가 매우 빠르기 때문에(Re≈10⁶) 점성효과를 무시하고 다음과 같은 순수 Forchheimer 법칙만을 직접 사용한다.

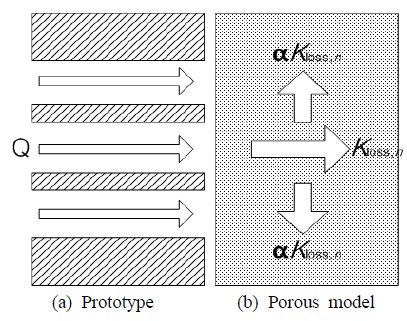
본 연구에서 다루고 있는 필터(타공판)는 동일한 크기를 가진 여러 개의 구멍이 판의 수직방향으로 일정하게 뚫려있기 때문에 판의 수직방향과 횡방향이 서로 다른 유동손실 특성을 가지고 있다[Figure 1(a) 참조]. 따라서 식 (2)에 있는 손실계수 K_loss는 수직방향과 횡방향이 서로 다르다. Figure 1(b)는 이에 대한 도식도(schematic)를 보여준다. 여기서 수직방향과 횡방향 손실계수는 각각 K_loss,n와 αK_loss,n로 표시하였다. 따라서 식 (2)는 다음과 같이 방향별로 다시 쓸 수 있다.

여기서 n과 t는 각각 수직방향과 횡방향 좌표를 말한다. 따라서 Forchheimer 법칙을 스트레이너의 압력 강하량 예측에 적용하기 위해서는 수직방향 손실계수 K_loss,n와 횡방향 손실계수 비(transverse loss coefficient multiplier) α에 대한 정보가 필요하다.

2.2 손실계수

다공성모델링 과정에서 필요한 두 방향의 손실계수는 일반적으로 경험식이나 실험식에 의존하는데, 이러한 정보가 주어지지 않을 경우 다음과 같이 수치적으로 구하는 방법을 설명한다.

먼저 수직방향 손실계수 K_loss,n은 타공판에 뚫린 구멍을 지나는 유동을 일반 파이프유동으로 가정하고, 이 유동에 대하여 간단한 수치모사를 수행하면 구해질 수 있다. 파이프의 직경과 평균 유동속도는 타공판 구멍의 경우와 동일하게 설정한다. 만약에 매우 긴 파이프에 평균속도 V_hole로 흐를 때 완전 발달된 유동(fully developed flow)에서 L만큼 떨어진 두 지점 사이의 평균 압력차가 ∆P라면 다음과 같이 수직방향 손실계수를 구할 수 있다.

여기서 φ는 타공판에서 타공판 전체 면적에 대한 총 구멍 면적의 비로 정의되는 공극율을 가리킨다.

반면에 횡방향 손실계수는 수직방향 손실계수에 비하여 구하기가 매우 어렵다. 본 연구에서는 타공판 위에 뚫려있는 구멍들이 규칙적으로 배열되어 있다는 사실에 착안하여 적절한 수치모사를 활용하여 구하는 방법을 제안한다[1]. 먼저 구멍들이 규칙적으로 배열되어 있기 때문에 유동손실 특성을 공유할 수 있는 최소한의 단위주기 형상을 가진 타공판만을 설정한다. 이어 설정된 단위주기 형상에 대하여 원형 수치모사를 수행한 후 정확한 압력 강하량을 구한다. 그리고 동일한 조건에 대하여 횡방향 손실계수 비를 바꾸어가면서 다공성모델 수치모사를 수행하고 압력 강하량을 구한다. 최종적으로 원형 수치모사와 같은 압력 강하량을 가져다주는 손실계수 비와 이에 해당되는 횡방향 손실계수가 우리가 구하고자 하는 최종 값이 된다.

3. 압력 강하량 예측

3.1 스트레이너

Figure 2:

View on a certain vertical cross sectionof the strainer

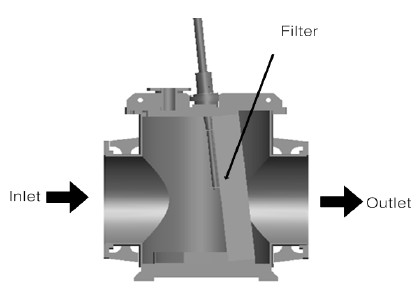
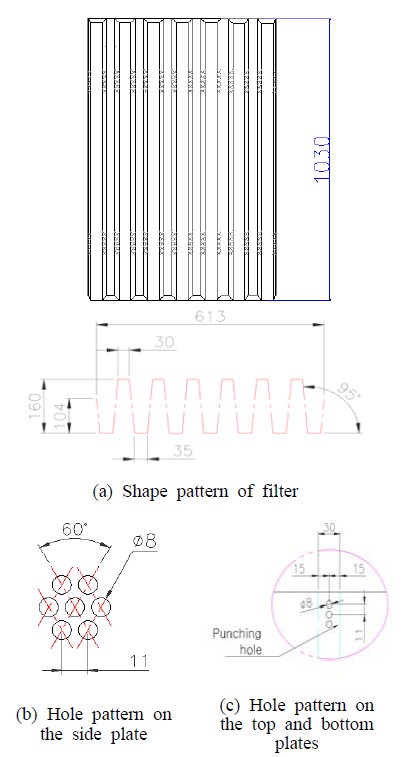
본 논문에서 다루는 스트레이너는 S 사에서 제작한 제품으로, 입구 직경이 φ600이다. Figure 2는 측면에서 본 스트레이너 전체형상의 단면을 보여주고 있다. 필터가 스트레이너 몸체 안에서 비스듬히 기울어져 있다. Figure 3(a)는 스트레이너 안에 설치되어 있는 필터(타공판)의 반복 형상을 보여주고 있다. 판금으로 제작된 필터는 위에서 바라보았을 때‘등변사다리꼴’모양이 연속적으로 반복되는 형상이다.

Figure 3(b) 및 (c)는 필터 내에 반복되는 형상인 등변사다리꼴 모양에서 각각 경사면과 상하면에 뚫려있는 구멍들의 배열을 보여준다. 경사면의 경우에는 φ8의 크기를 가진 다수의 구멍들이 일정한 규칙으로 배열되어 있기 때문에 본 연구에서는 이 부분 전체를 다공성 매질로 가정하였다. 반면에 상하면의 경우에는 φ8의 구멍들이 단 한 줄로만 배열되어 있기 때문에 이 부분에 대해서는 다공성모델링을 적용하지 않았다.

Figure 3:

Shape details of the filter (perforated plate) installed in the strainer

3.3 스트레이너 해석

앞서 제시한 다공성모델링 기법을 스트레이너 압력강하 해석에 적용하였으며, 본 절에서는 그 과정과 결과를 상세히 소개한다.

3.3.1 손실계수 측정

다공성 매질에 부과할 수직방향 손실계수(K_loss,n)를 측정하기 위하여 타공판 구멍과 같은 크기인 φ8 직경과 충분한 길이를 가지는 파이프 유동에 대하여 유동해석을 수행하였다. 이때 입구유속은 앞서 설명한 바와 같이 V_hole = 1.08 m/s을 부과하였다. 해석결과를 식 (5)와 (6)에 대입하여 최종적으로 수직방향 손실계수 K_loss,n = 14.7 /m을 얻었다.

Table 1:

Boundary conditions and parameters applied to the numerical simulations on the unit shape pattern of the strainer A

Figure 4:

Unit shape pattern of filter simulated to obtain the transverse loss coefficient in the strainer

Figure 5:

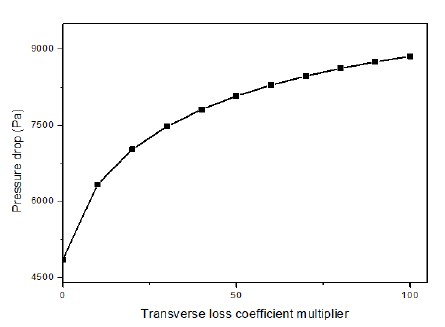
Variation of the pressure drop with the transverse loss coefficient multiplier for the unit shape pattern of the strainer

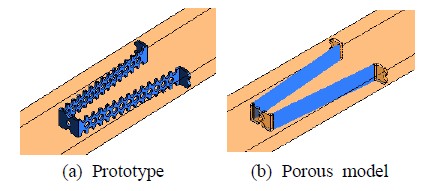
이어 필터(타공판)로부터 반복된 형상과 유동 손실특성을 공유할 수 있는 단위주기 형상을 설정하였으며, 그 형상을 Figure 4에 나타내었다[1]. Figure 4(a)는 원형에 대한 단위주기 형상을 보여주며, Figure 4(b)는 타공판의 경사면을 다공성 매질로 대체한 다공성모델에 대한 형상을 보여준다. 물론 길이, 높이 및 두께는 서로 동일하다. 설정된 단위주기 형상에 대하여 먼저 원형 수치모사를 수행하였으며, 부과된 경계조건은 Table 1에 나타내었다. 이어 동일한 경계조건을 부과하고 다공성모델 수치모사를 역시 수행하였다. 이때 앞서 구한 수직방향 손실계수를 부과하였으며, 횡방향 손실계수 비 α을 바꾸어 가면서 다공성모델 수치모사를 수행하고 압력 강하량을 계산하였다. Figure 5는 다공성모델 수치모사를 통하여 얻어진 횡방향 손실계수 비와 단위형상에 대한 압력 강하량과의 관계를 보여준다. 최종적으로 원형 수치모사와 모델 수치모사 사이에 가장 근접한 압력 강하량을 가져다주는 횡방향 손실계수를 구하였으며, 그 결과는 α = 14.6이다. 본 연구에서는 설정된 계산영역을 좌우로 배씩 늘려 수치해석을 추가적으로 수행하였으나, Figure 5에 보여준 단위주기에 대한 결과와 거의 차이가 없음을 확인하였다.

3.3.2 단위형상 유동해석

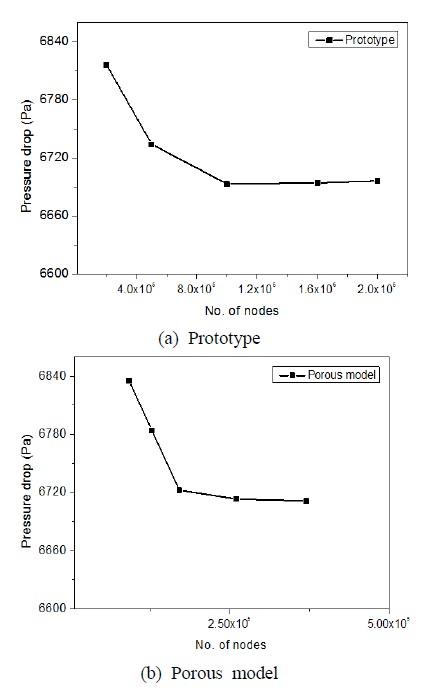
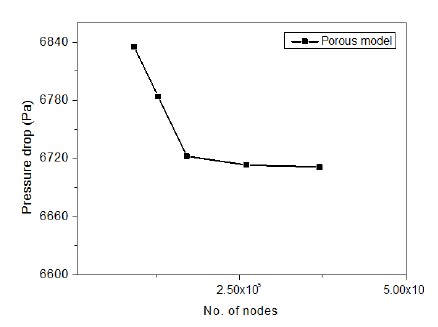
Figure 4에서 보여준 단위주기 형상에 대하여 K_loss,n = 14.7 /m과 α = 14.6을 부과하고 수행한 다공성모델 수치모사 결과를 원형 수치모사 결과와 함께 상호비교 목적으로 Figures 6-9에 보여주고 있다. 먼저 Figure 6은 원형과 다공성모델 수치모사에 대한 격자-수렴성 시험(grid-independence test or spatial convergence test) 결과를 보여준다. 안정화된 결과를 얻기 위해서는 원형의 경우 적어도 약 100만개 정도의 격자가 필요한데 반하여, 모델의 경우 약 25만개 정도의 격자만이 필요하였다. 이 비교결과를 통해서 다공성모델이 경제적으로 매우 효과적이라는 사실을 잘 알 수 있다.

Figure 7은 평균 유동속도(V_in) 변화에 따른 단위형상 스트레이너를 지나는 유동의 압력 강하량을 보여준다. 속도가 증가하면 압력 강하량이 포물선 형태로 증가하였다. 특히 다공성모델링 기법은 정격유량 V_in = 2.5 m/s(V_unit = 1.69 m/s에 해당) 근처에서 압력 강하량을 정확하게 예측할 수 있음을 잘 보여주고 있다.

Figure 6:

Grid-independence test on the unit shape pattern for the strainer

Figure 7:

Comparison of pressure drop versus average inlet velocity (strainer) between the prototype and porous-model numerical simulations on the unit shape pattern for the strainer

Figure 8:

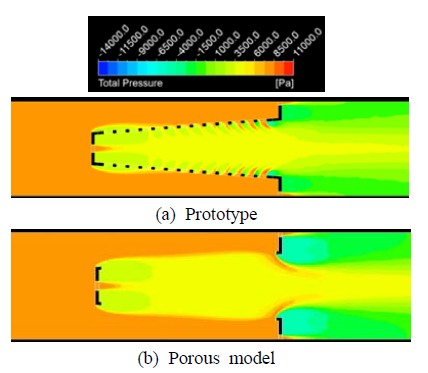
Distributions of total pressure on a horizontal cross section obtained from the numerical simulations on the unit shape pattern of the strainer

Figure 9:

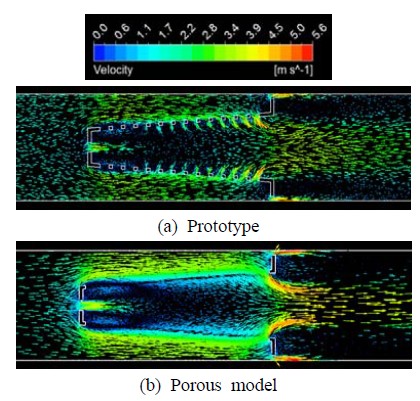
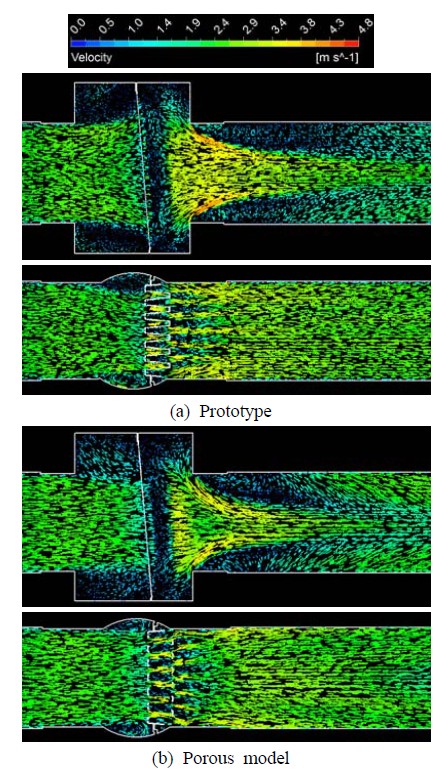
Distributions of flow velocity on a horizontal cross section obtained from the numerical simulations on the unit shape pattern of the strainer

Figure 8과 9는 각각 단위주기 형상에 대하여 전압력(total pressure)과 속도 분포를 보여준다. 비록 타공판 구멍을 통한 유동과 다공성매질을 통한 유동은 명확히 서로 다르지만 전체적인 압력과 속도 분포는 정성적으로 잘 일치함을 알 수 있다. 이러한 결과는 다공성모델링 기법의 정확성을 잘 말해준다.

3.3.3 전체형상 유동해석

Figure 10:

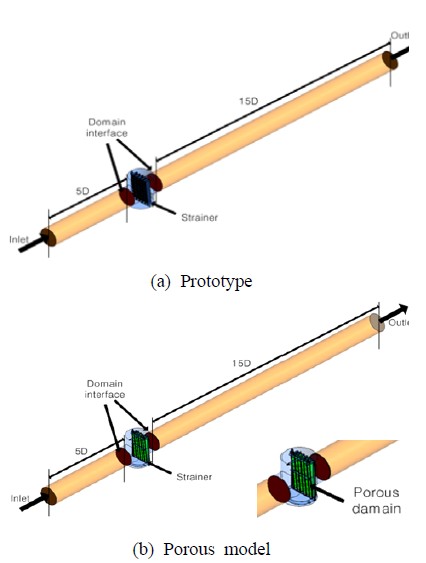
Schematics illustrating the computational domains for the numerical simulations on the whole shape pattern of the strainer

본 논문에서 제시한 다공성모델링 기법의 유효성을 검증하기 위하여 단위주기 형상에 대한 수치모사로부터 얻어진 손실계수를 부과하여 스트레이너 전체형상에 대한 다공성모델 수치모사를 수행하였다. 동시에 모델링의 성능을 평가하기 위해 같은 형상과 조건에 대해서도 원형 수치모사를 역시 수행하였다. Figure 10(a)와 (b)는 스트레이너 전체형상에 대하여 각각 원형 수치모사와 다공성모델 수치모사를 수행하기 위한 계산영역을 보여주고 있다. 양 수치모사에서 유일한 차이는 타공판과 다공성매질뿐이다. 계산영역은 입구 측 관로, 스트레이너 및 출구 측 관로 등 크게 세 부분으로 나누어져 있으며, 유동의 안정화와 경계조건의 영향을 최소화하기 위하여 입구와 출구 측 관로는 각각 관로 직경(φ600)의 5배와 15배까지 늘렸다.

Figure 11은 전체형상의 원형과 다공성모델에 대하여 어느 수평 단면 위 필터 주위에 발생시킨 격자 모습을 보여주고 있다. 스트레이너 해석을 위해 연장한 입구 및 출구 측의 관로에는 단순한 형상 때문에 정렬 격자(structured mesh)를 그리고 스트레이너 몸체 부분에는 복잡한 형상 때문에 사면체 격자(tetrahedral mesh)를 사용하였다. 참고로 본 수치모사에서는 원형의 경우 약 1300만개를 그리고 다공성모델의 경우 약 400만개의 노드를 사용하였다. 이는 전체형상에 대해서 격자-수렴성 시험을 통해 얻어진 최소 필요 노드 수이다. 전체형상에 대한 수치모사를 수행하기 위하여 필요한 경계조건과 매개변수들은 Table 2에 정리하였다.

Figure 11:

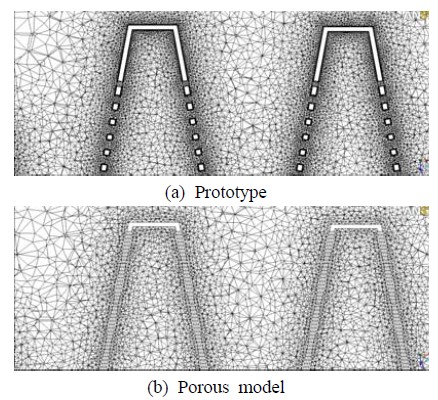
Meshes generated around the filter for thenumerical simulations on the whole shape pattern of the strainer

Table 2:

Boundary conditions and parameters applied to the numerical simulations on the whole shape pattern of the strainer

Figure 12:

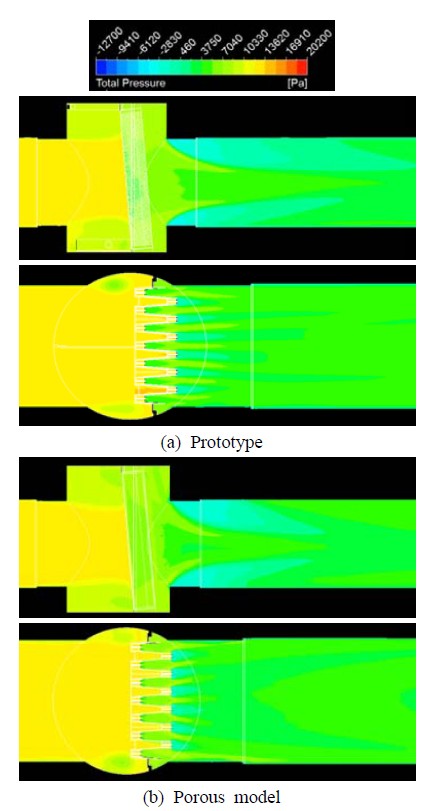
Distributions of total pressure on certain vertical (upper) and horizontal (lower) cross sections obtained from the numerical simulations on the whole shape pattern of the strainer

스트레이너 전체형상에 대한 원형 수치모사와 다공성모델 수치모사를 수행하였으며, 그 결과는 Figure 12와 13에 나타내었다. Figure 12는 스트레이너 근처에서의 전압력 분포를 보여준다. 타공판과 다공성매질 사이에 구조적인 차이가 존재함에도 불구하고 정성적인 압력분포는 매우 잘 일치하였다. 스트레이너를 지나는 압력 강하량은 원형 수치모사와 다공성모델 수치모사에 의해 각각 ∆P = 10,285 Pa과 ∆P = 10,230 Pa로 예측되어 양 결과 사이에는 거의 오차가 없이 매우 정확함을 알 수 있다. Figure 13은 유동속도 분포를 보여주는데, 근본적인 구조 차이(타공판과 다공성매질) 때문에 필터 근처에서 양 결과 사이에 미세한 흐름의 차이는 발생하지만 전체적인 양상은 서로 잘 일치하였다.

Figure 13:

Distributions of flow velocity on certainvertical (upper) and horizontal (lower) cross sections obtained from the numerical simulations on the whole shape pattern of the strainer

4. 결론

본 논문에서 얻어진 결론은 다음과 같다.

1.본 논문에서 다루고 있는 스트레이너는 매우 빠른 유동속도를 수반하기 때문에(Re≈10⁶) 점성효과를 무시하고 관성효과만을 고려하는 Forchheimer 법칙을 적용하여 그 유효성을 확인하였다.

2.Forchheimer 법칙을 적용하기 위하여 간단한 파이프유동 해석을 통하여 수직방향 손실계수를 구하였다. 이어 필터 내에서 반복되는 형상을 대표할 수 있는 단위형상을 설정한 후 원형과 다공성모델에 대하여 각각 유동해석을 수행하고, 원형과 모델 수치모사 사이에 해석결과를 서로 비교하여 횡 방향 손실계수를 구하였다.

3.제안된 다공성모델링 기법을 검증하기 위하여 스트레이너 전체형상에 적용하였으며, 그 모델링 결과를 원형 수치모사 결과와 비교하였다. 비교 결과 제안된 모델링 기법은 압력 강하량뿐만 아니라 속도장 및 압력 분포 등 유동특성을 비교적 정확히 예측하였다. 게다가 계산비용도 현저히 줄일 수 있었다.

Acknowledgments

본 연구는 2012년도 지식경제부의 재원으로 한국에너지 기술평가원(KETEP)의 지원을 받아 수행한 연구 과제(No. 20114030200030)이며, 정일선의 석사학위논문(“선박용 스트레이너 압력강하 해석에 관한 연구, 동아대학교 대학원”)을 개선한 것이다.

References

• B. Y. Guo, F. Hou, A. B. Yu, L. F. Li, and J. Guo, “Numerical modelling of the gas flow through perforated plates”, Chemical Engineering Research and Design (in press), (2012). [https://doi.org/10.1016/j.cherd.2012.10.004]
• Y. Zhu, P. J. Fox, and J. P. Morris, “A pore-scale numerical model for flow through porous media”, International Journal of Numerical and Analytical Methods in Geomechanics, 23(9), p881-904, (1999). [https://doi.org/10.1002/(SICI)1096-9853(19990810)23:9<881::AID-NAG996>3.0.CO;2-K]
• J. Dufrêche, M. Prat, P. Schmitz, and J. D. Sherwood, “On the apparent permeability of a porous layer backed by a perforated plate”, Chemical Engineering Science, 57(15), p2933-2944, (2002). [https://doi.org/10.1016/S0009-2509(02)00173-2]
• F. Depypere, J. G. Pieters, and K. Dewettinck, “CFD analysis of air distribution in fluidised bed equipment”, Powder Technology, 145(3), p176-189, (2004). [https://doi.org/10.1016/j.powtec.2004.06.005]
• A. Grahn, E. Krepper, S. Alt, and W. Kästner, “Implementation of a strainer model for calculating the pressure drop across beds of compressible, fibrous materials”, Nuclear Engineering and Design, 238(10), p2546-2553, (2008). [https://doi.org/10.1016/j.nucengdes.2008.04.010]
• A. M. Hayes, J. A. Khan, A. H. Shaaban, and I. G. Spearing, “The thermal modeling of a matrix heat exchanger using a porous medium and the thermal non-equilibrium model”, International Journal of Thermal Sciences, 47(10), p1306-1315, (2008). [https://doi.org/10.1016/j.ijthermalsci.2007.11.005]
• A. Grahn, E. Krepper, F.-P. Weiß, S. Alt, W. Kästner, A. Kratzsch, and R. Hampel, “Implementation of a pressure drop model for the CFD simulation of clogged containment sump strainers”, Journal of Engineering for Gas Turbines and Power, 132(8), p082902(9 pages), (2010). [https://doi.org/10.1115/ICONE17-75249]
• G. Venugopal, C. Balaji, and S. P. Venkateshan, “Experimental study of mixed convection heat transfer in a vertical duct filled with metallic porous structures”, International Journal of Thermal Sciences, 49(2), p3406-348, (2010). [https://doi.org/10.1016/j.ijthermalsci.2009.07.018]
• B. Molin, “Hydrodynamic modeling of perforated structures”, Applied Ocean Research, 33(1), p1-11, (2011). [https://doi.org/10.1016/j.apor.2010.11.003]
• Y. Bae, Y.-E. Jeong, and Y. J. Moon, Moon,“Computation of flow past a flat plate with porous trailing edge using a penalization method”, Computers and Fluids, 66(6), p39-51, (2012). [https://doi.org/10.1016/j.compfluid.2012.06.002]
• F. A. L. Dulien, Porous Media Fluid Transport and Pore Structure, Academic, (1979).