Fluid-structure interaction analysis on a low speed 200 W-class gyromill type vertical axis wind turbine rotor blade

2.1 수치해석 모델 및 유동장

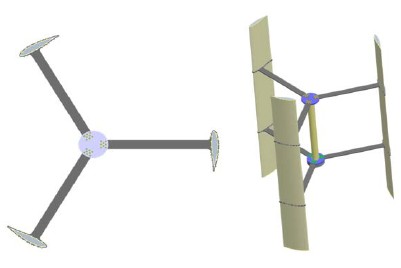
Figure 1은 해석 모델인 자이로밀형 수직축 풍력터빈 로터 블레이드에 대한 3차원 형상을 나타낸다. 블레이드 수는 총 3매이며, 타워와 회전축에서 블레이드를 지지하는 스트럿 구조로 구성되어 있다. 수치해석의 수렴성 등을 고려하여 수치해석 결과에 영향을 미치지 않는다고 판단되는 부수적인 영역들의 구조는 간략화 하였다.

Table 1은 풍력터빈 모델의 상세 사양을 나타내고 있다. NACA63415 익형, 정격풍속 10 m/s, 로터반경 0.63 m, 블레이드 높이 2 m, 블레이드 코드 길이 0.23 m, 로터 회전수 200 rpm으로 설계하였다.

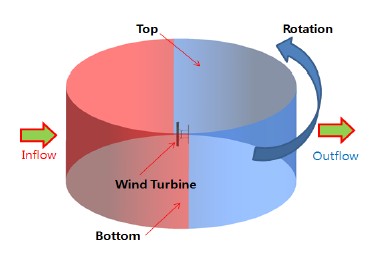
Figure 2는 전체유동장 및 경계조건을 나타내고 있다. 유동해석시 수렴성을 높이기 위하여 블레이드 회전 반경을 기준으로 15배 크기의 넓은 원통 형상으로 생성하였다.

Figure 1:

Numerical model of 200 W class gyromill type vertical axis wind turbine rotor blade.

Table 1:

Specification of 200 W-class Gyromil type vertical axis wind turbine model.

Figure 2:

Overall view of flow filed and boundary conditions of 3-D numerical flow field.

2.2 계산격자

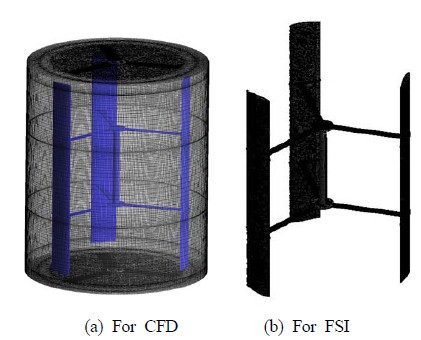
Figure 3은 수치해석 유동장의 풍력터빈 로터 블레이드 모델을 기반으로 생성된 유동해석 및 구조해석용 3차원 계산격자계를 나타낸 것이다.

Figure 3(a)의 격자계는 전체 유동장 중 로터 블레이드를 포함하는 회전영역에 대한 격자계를 보이고 있으며, 유동해석을 위한 전체유동장의 노드수는 약 980만개로 설정하였다. 복잡한 해석 형상 및 해석 효율성을 고려하여 육면체 (hexahedral), 사면체 (tetrahedral), 삼각기둥 (wedges) 격자를 혼용하여 구성하였다. 유동장 전체에 대해서 벽면 근접 격자 간격은 y+≦15로 설정하여 계산의 수렴성을 고려하였다.

또한, 본 연구에서는 단방향 유체-구조 연성 해석을 수행하기 위한 구조 해석격자를 Figure 3(b)에서 나타내었으며 사면체(tetrahedral)격자계로 구성하였다. 해당 전체 노드 수는 약 15만개로 이루어져 있다.

Figure 3:

Numerical grid system of wind turbine.

2.3 유동해석 경계조건

본 연구에서 자이로밀형 수직축 풍력터빈 로터 블레이드의 유동해석을 위해 설정한 경계조건은 Figure 2에서 개략적으로 보이고 있다.

3차원 유동장에서 블레이드는 회전운동만 하기 때문에 블레이드 주위의 회전영역과 그 외의 고정영역으로 구분하는 경계조건을 입력하였다. 회전영역과 고정영역을 동시에 포함하는 유동해석 기법 중 유동 데이터를 두 영역에 서로 전달하기 위한 경계 조건으로 GGI Interface기법을 적용하였다. 원통형 유동장의 반쪽 영역은 입구, 그 반대에는 출구 영역으로 설정하였다. 입구에는 풍속 10 m/s와 60 m/s를, 출구와 유동장 윗면과 바닥면에는 Opening 조건을 주었고, 과도해석 수행시 내부 회전영역은 200 rpm으로 회전하도록 설정하였다.

발전기로부터 정격출력 범위 이상의 출력이 발생할 경우 제어시스템에 의하여 풍력발전기 로터는 회전하지 않도록 정지를 하게 되며 이 상태로 극한 풍속을 견디게 된다. 이러한 조건으로 극한 풍속 조건 해석시에는 하나의 블레이드가 풍향에 수직하게 세워둔 상태에서 회전이 없는 조건으로 해석을 진행하였다.

유동해석 난류모델은 풍력발전 유동해석 분야에서 널리 사용되며 층류로부터 난류로의 천이영역에 대한 높은 신뢰성을 가진 k-ω모델 기반의 SST(Shear Stress Transport)모델을 적용하였다. 풍력터빈 유동장에 대한 수치해석은 상용코드 ANSYS CFX[7]로 수행하였다.

200 W급 자이로밀형 수직축 풍력터빈 로터 블레이드에 대한 단방향 유체-구조 연성 해석은 유동해석결과에서 블레이드 표면, 축, 스트럿 등에 작용하는 하중을 추출하여 적용한다. 즉, 단방향 유체-구조 연성 해석에서는 유동해석 결과인 유동영역과 구조영역의 경계면에서 발생하는 압력 데이터를 구조해석 모델에 전달하게 된다.

Talbe 2는 유동해석 경계조건을 나타내고 있다.

Table 2:

Boundary conditions of 3-D CFD analysis for a 200 W class gyromil type vertical axis wind turbine.

Figure 4:

Load condition mapped using the results from CFD analysis.

2.4 하중 경계조건

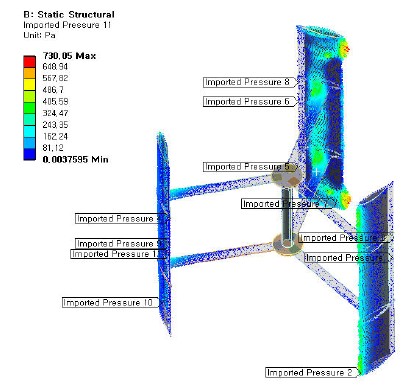
Figure 4는 유동해석으로부터 추출된 하중을 보여주고 있다. 그리고 이 하중은 절점에서 계산 되는 X방향, Y방향, Z방향의 힘으로 나타나 있다.

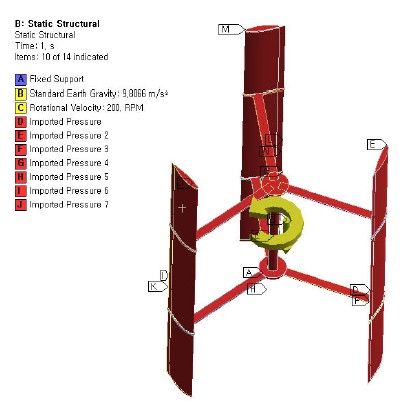
단방향 유체-구조 연성 해석을 수행하기 위해서는 유동해석 결과로 도출된 압력데이터를 구조해석의 동일한 부분에 적용하여 하중데이터를 매핑(mapping)해야 한다. 또한, 구조해석에서도 회전조건으로서 본 연구에 적용된 풍력터빈 로터 블레이드의 회전수인 200 rpm을 적용하였고, 자중에 대해서도 하중 경계조건으로서 부여하였다. Figure 5는 회전수 및 자중에 대한 하중경계조건을 설정한 결과를 보이고 있다.

구조건전성 평가를 위해 최대설계 풍속 조건인 60m/s상태를 적용하였으며 이때 풍력터빈 로터 블레이드의 회전은 없이 자중만 적용하였다.

2.5 재료물성 데이터

Table 3은 본 연구에 적용한 200 W급 자이로밀형 수직축 풍력터빈 로터의 블레이드와 스트럿에 대한 재료 물성치 데이터를 나타내고 있으며, 재질은 모두 Al6061로 구성하였다. 회전축과 타워는 SS400으로 구성되어 있다.

Figure 5:

Rotational speed and dead load setup.

Table 3:

Data of material properties.

3.1 표면압력분포

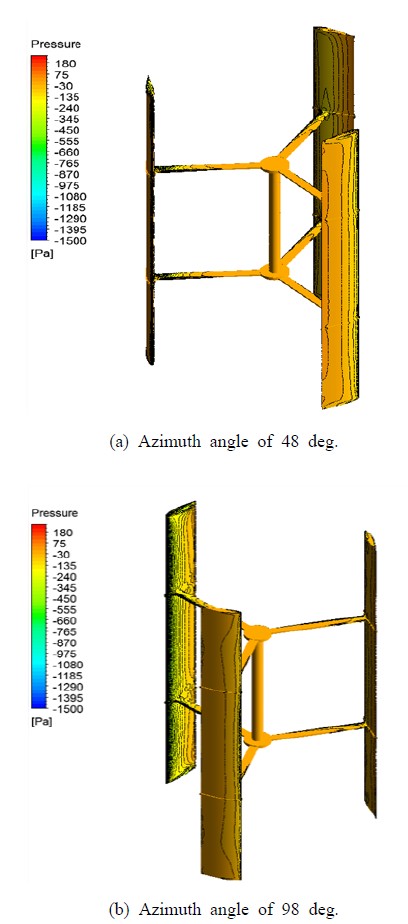
Figure 6은 정격 풍속에 의한 과도 해석에서 구해진 로터 블레이드 표면에서의 압력분포를 나타내고 있으며, 방위각에 따라서 각 블레이드 표면압력이 변화함을 알 수 있다. 또한 블레이드의 흡입면이 압력면 보다 압력이 낮은 것을 확인 할 수 있는데 이러한 현상이 풍력터빈의 동력을 만들게 되는 중요한 현상이다.

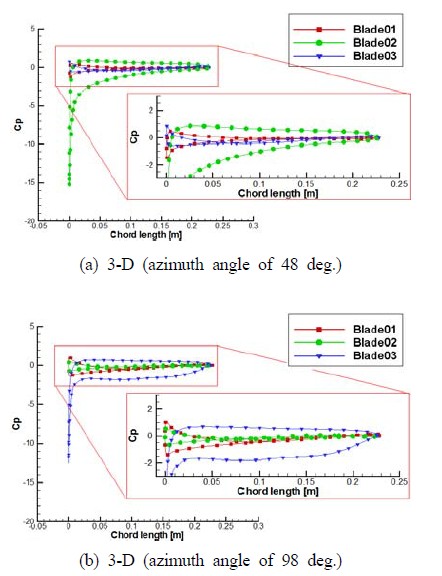
Figure 7은 로터 중앙 단면에서의 블레이드 압력 선도를 나타내고 있다. 흡입면과 압력면의 압력차이가 클수록 로터를 회전시키는 힘이 커지게 되는데 Figure 7에서 보이듯이 3개의 블레이드 중에서 압력차이가 큰 블레이드가 하나씩 존재한다. 로터의 방위각이 바뀌면서 큰 압력차를 가지는 블레이드는 바뀌게 되며 이러한 현상이 연속적으로 발생하면서 로터는 회전력을 지속적으로 가지게 된다.

Figure 6:

Pressure distribution on rotor blade surface by CFD Transient analysis

Figure 7:

Pressure coefficient by 3-D CFD analysis

3.2 FSI해석에 의한 구조 안정성 평가

CFD해석으로부터 얻어진 블레이드, 스트럿, 축의 각 표면에서 발생하는 압력데이터를 구조해석 모델에 적용하고, 단방향 유체-구조 연성 해석 기법을 적용하여 총변형량, 등가응력, 안전율에 대한 해석결과를 확보하였다

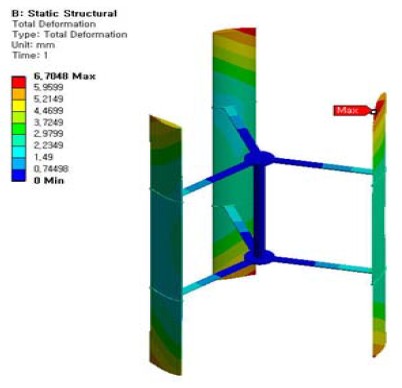
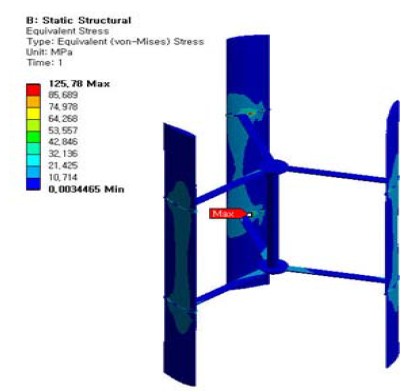
Figure 8은 정격풍속 10 m/s에서 방위각이 48 deg.인 Case 1에서의 풍력터빈 로터 블레이드에서 발생하는 변위분포를 보이고 있다. 최대변위는 블레이드의 최상부 끝단 측면의 후연 부근에서 발생하였으며, 6.70 mm의 변형량을 나타내었다. 또한, 응력분포에 대한 해석결과도 Figure 9에서 보이고 있으며, 블레이드 표면과 스트럿의 접촉부에서 응력집중이 발생하여 최대등가응력이 높은 값을 나타내고 있다.

Table 4는 정격 풍속 10 m/s에서 2종류의 서로 다른 방위각에 따른 해석결과와 극한 풍속 60 m/s에서의 해석결과로부터 총변형량, 등가응력, 안전율에 대한 비교를 보이고 있다.

Figure 8:

Total deformation (Case 1; Azimuth angle of 48 deg. in Transient analysis)

Figure 9:

Equivalent stress (Case 1; Azimuth angle of 48 deg. in Transient analysis)

CFD해석 결과에서 확인한 바와 같이 방위각에 따라서 각 블레이드 표면 압력 분포가 다르게 나타나는 것처럼 변형량 및 등가응력도 약간의 차이를 나타냄을 알 수 있다. Case 1에서 최대 등가응력이 125.78 MPa이고 본 해석에 적용한 Al6061 항복강도가 280 MPa이므로 안전율이 2.22의 결과를 도출하였다.

Figure 10:

Total deformation (Case 3; Extreme wind speed: 60m/s)

Figure 11:

Equivalent stress (Case 3; Extreme wind speed: 60m/s)

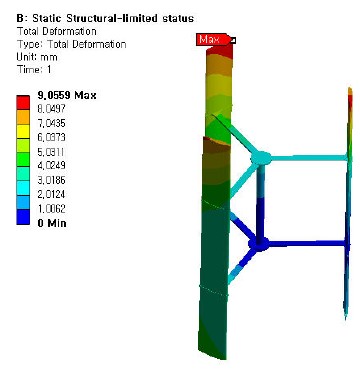
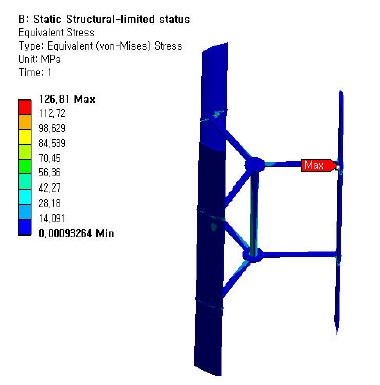
Figure 10은 극한 풍속 60m/s에서 풍력터빈 로터 블레이드에서 발생하는 변위분포이고, 최대 변위는 블레이드 최상부 끝단 측면의 후연 부근에서 9.05 mm의 변형량을 나타내었다. 또한, 응력분포에 대한 해석결과도 Figure 11에서 보이고 있으며, 블레이드 표면과 스트럿의 접촉부에서 최대 등가응력이 발생하였다. 이때 발생한 최대등가응력은 126.81 MPa이고 본 해석에

Table 4:

Evaluation of structural stability.

적용한 Al6061 항복강도가 280 MPa이므로 안전율 2.21이므로 본 연구에 적용한 로터 블레이드는 설계 운전점에서 구조적으로 안전하다고 판단된다.