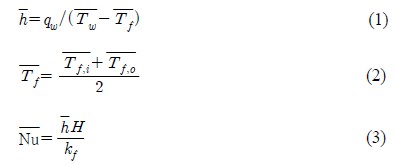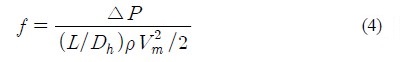Numerical study on the pressure drop and heat transfer enhancement in a flat-plate solar collector
The use of artificial roughness in various forms of shapes and sizes is the most common and effective way to improve the performance of a flat-plate solar collector. In the present study, numerical analysis on heat transfer and pressure drop was performed in a rectangular channel with various rib arrays. The uniform heat flux is applied to the channel from the upper side. The forms of ribs considered in this study were rib 90°, groove 90°, groove 60°, baffle 90°, baffle 60°, wave 90° and wave 60°. Air is the working fluid, and the Reynolds number ranges from 3200 to 17800. Nusselt number and friction factor were investigated to predict the performance of the system with various type of ribs. The average Nusselt number and pressure drop were increased with the increase of velocity in all types of ribs. The highest heat transfer and pressure drop occurred for the baffle 90°, but highest performance factor considering heat transfer and pressure drop together occurred for the groove 60°. Therefore, heat transfer and pressure drop should be considered together when a flat plate solar collector is designed.
초록
평판형 태양열 집열기의 성능을 향상시키기 위하여 다양한 형태의 형상과 크기의 인공 거칠기가 가장 일반적이고 효과적으로 사용된다. 본 연구에서는 다양한 형상의 립을 삽입한 사각 채널에서의 열전달 특성 및 압력강하에 대하여 수치해석을 수행하였다. 사각 채널의 윗 평판에 일정한 열유속을 가하였다. 삽입된 립의 형상은 rib 90°, groove 90°, groove 60°, baffle 90°, baffle 60°, wave 90°, wave 60° 모델이다. 작동유체는 공기이며 Reynolds 수는 3200∼17800의 범위이다. 다양한 형태의 립 형상에 따른 시스템의 성능을 예측하기 위하여 Nusselt 수와 마찰인자를 고찰하였다. 모든 형태의 립에서 속도가 증가할수록 Nusselt 수와 압력강하는 증가하였다. 열전달 향상과 압력강하가 가장 높은 모델은 baffle 90° 모델이지만, 열전달 특성과 압력강하를 고려하여 나타낸 성능계수에서는 groove 60° 모델이 가장 크게 나왔다. 따라서 평판형 태양열 집열기에서는 열전달 향상과 압력강하를 항상 동시에 고려한 설계가 필요하다.
Keywords:
Solar collector, Heat transfer enhancement device, Heat transfer characteristics, Pressure drop, Performance factor, 태양열 집열기, 열전달 향상 장치, 열전달 특성, 압력강하, 성능계수1. 서 론
태양열을 이용한 온수 및 냉·난방에 관한 연구는 오래전부터 이루어져 왔다. 태양열은 무공해, 무한량, 무가격의 청정에너지원으로서 기존의 화석에너지에 비해 지역적 편중이 적은 분산형 에너지원이다. 또한 지구온난화 대책으로 온실가스 배출을 저감할 수 있는 재생 가능 에너지원이며, 안정적인 열원을 확보할 수가 있고 석탄 및 천연가스등의 화석연료 고갈에 대한 대체 에너지로 주목을 받아왔다[1].
태양열시스템은 태양으로부터 에너지를 모으는 집열부, 모아진 열을 저장했다가 필요 시 사용하는 축열부, 태양열 축열조에 저장된 태양열을 공급하고 사용량이 부족할 경우 보조열원에 의해 공급을 하는 이용부, 태양열을 효과적으로 집열, 축열, 공급하기 위한 조절장치인 제어장치 등으로 크게 4가지로 나눌 수가 있다. 그 중에서도 에너지의 밀도가 낮고 생산이 간헐적인 태양에너지를 효율적으로 이용하기 위해서는 집열기의 역할이 매우 중요하다.
평판형 태양열 집열기의 효율을 높이기 위한 방법으로 열전달 향상 장치의 삽입, 표면 거칠기의 변화 등 다양한 방법들이 알려져 있다. 그 중에서 열전달 향상 장치로서 립(rib)의 삽입은 작동유체의 유동교란을 일으켜 열전달 성능을 잘 향상시킨다고 알려져 있다[2][3].
Bhushan과 Singh[4]은 집열기 평판에 돌출부를 엇갈리게 배열하여 열전달면적을 확장시켜 Reynolds 수 4000-20000 범위에서 열전달과 마찰인자에 대한 특성에 대하여 고찰하였다. Aharwal et al. [5]은 유동방향에 60°로 기울어진 립과 함께 상대적 갭 위치, 갭 너비를 도입하여 최적의 위치를 찾아내었고, Karmare와 Tikekar[6]는 metal grit rib의 형상을 도입하여 Reynolds 수 4000-17000 범위에서 열전달 향상에 대하여 연구하였다. Hans et al. [7]은 유동방향에 수직하는 V립을 도입하여 상대적 거칠기 너비를 변화시켜 최적의 V립에 대하여 연구를 하였다. Akpinar와 Kocyigit[8]은 덕트 내에 배플(baffle)형태의 유로를 만들고 유로 사이에는 삼각형, 잎 모양, 45°로 기울어진 직사각형의 장애물을 설치하여 열적특성에 대하여 연구하였다. Kumar et al. [9]은 3000-15000의 Reynolds 수 범위에서 W립에 대한 형상을 삽입하여 열전달과 마찰인자에 대하여 고찰하였고, Singh et al. [10]은 부서진 V-down 립들에 대해서 2차유동의 발생 등에 대하여 논의하였다.
본 연구에서는 기존의 타 연구자의 실험에서 밝혀진 여러 가지 열전달 향상 장치의 형상에 대한 수치해석을 수행하여 수치해석 결과의 타당성을 검증하고, 새로운 형상 및 배열의 장치를 삽입하여 수치해석을 수행하고자 한다. 이를 통해 시간 및 자원을 줄이고, 복잡한 실험장치를 간단히 재현하고, 시뮬레이션을 통하여 열전달 특성과 압력강하를 구하여, 그들의 특징을 알아보고 효율적인 열전달 향상 장치를 찾고자 한다.
2. 수치해석
2.1 수치해석 모델 및 경계조건
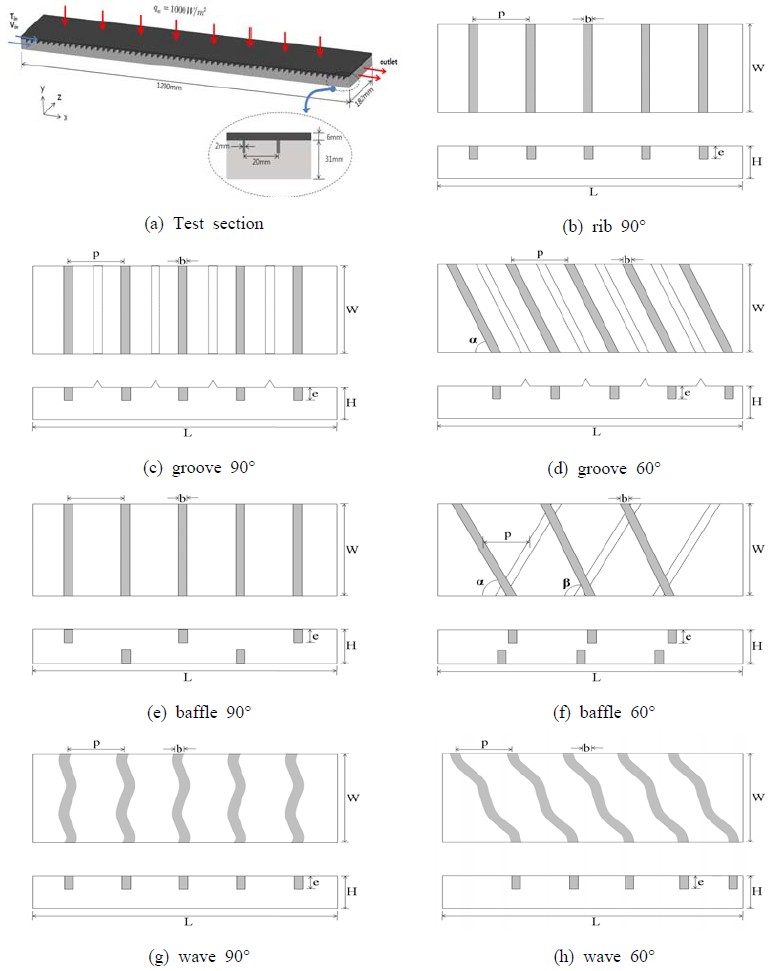
새로운 형상 및 여러 가지 변수를 도입하여 효율적인 열전달 향상장치를 알아내기 위해서 여러 가지 형상을 모색하여 모델링을 하였다. Figure 1은 수치해석 모델의 실험부와 열전달 향상 장치의 형상을 보여주고 있다. (a)는 실험부의 전반적인 형상을 보여주고 있다.
실험부는 1200(L) × 182(W) × 31(H)mm이며, 실험부 앞에는 완전발달된 유동을 위해 800mm의 덕트가 설치되어 있고 실험부 뒷부분에는 600mm의 덕트가 설치되어 있다. 입구에서 온도가 20°C인 공기가 유입되며, 실험부에서는 윗면에 일정한 열유속(qw) 1000W/m2이 주어지고, 덕트의 외부는 모두 단열되어 있다. 흡열평판과 부착된 열전달 향상 장치의 재질은 모두 알루미늄이다. 수력직경(Dh)은 53mm이고, 입구유속은 0.96m/s∼5.34m/s이며 이는 Reynolds 수가 3200∼17800에 해당하고, 비원형덕트에서 난류영역에 해당한다.
Figure 1에서 (b)∼(h)는 열전달 향상 장치의 형상을 나타내고 있다. (b) rib 90° 모델은 립이 유동방향에 90°로 배열되어 있는 형상이다. (c) groove 90° 모델은 립이 유동방향에 90°로 피치가 20mm로 배열이 되어 있으며, 립과 립의 중간에 홈이 파여져 있는 형상이다. (d) groove 60° 모델은 유동방향에 60°로 기울어져 배열되어있으며 립과 립 사이에 유동방향에 60°로 기울어진 홈이 파여져 있다. (e) baffle 90° 모델은 립이 유동방향에 90°이며 윗면과 아랫면에 피치 20mm간격으로 지그재그 형식으로 배열되어있는 형상이다. (f) baffle 60° 모델은 립이 윗면과 아랫면에 지그재그형식이며 피치가 20mm간격으로 기울어져 배열되어있고 윗면에 붙어있는 립은 유동방향에 60°, 아랫면에 붙어있는 립은 유동방향에 120°로 기울어져 배열되어 있다. (g) wave 90° 모델은 물결모양의 형상을 가진 립으로서 유동방향에 90°로 배열되어 있다. (h) wave 60° 모델은 물결모양의 형상을 가진 립으로서 유동방향에 60°로 기울어져 배열되어 있다.
Table 1은 각각의 형상에 대하여 피치와 립의 높이 비(p/e), 립의 높이(e)와 폭(b), 립의 높이와 수력직경의 비(e/Dh), 덕트의 폭과 높이의 비(W/H), 작동유체의 유동방향과 윗 립이 이루는 각도(α), Reynolds 수의 범위 등 각종 변수들을 나타내고 있고 이에 따라 수치해석을 수행하였다.
2.2 수치해석 방법
본 수치해석에서는 평판형 태양열 집열기의 내부에 부착된 열전달 향상 장치의 영향에 따른 열전달 및 압력강하의 특성을 모사하기 위하여 열유체 상용해석 프로그램인 FLUENT[11]를 사용하였다. Navier-Stokes 방정식은 연속적인 위치에서 미지수를 지니고 있는 미분방정식이므로 근사해를 구하기 위한 이산화 방법으로 유한체적법(Finite Volume Method)을 사용하였다.
앞에서 보았듯이 본 수치해석은 난류영역에 해당하기 때문에 경계층 외부의 해석에 뛰어난 성능을 지닌 표준 k-ε난류모델을 사용하였으며, 벽면에서는 조밀한 격자를 생성하여 정확한 해석을 얻기 위하여 Enhanced Wall Treatment를 적용하였다. 대류항의 차분에는 멱승도식(Power law scheme)을 사용하였으며, 압력장의 처리에 있어서 압력-속도의 연계해석은 SIMPLEC (SIMPLE-Corrected)알고리즘을 사용함으로써 압력은 연속방정식과 운동량방정식으로부터 간접적으로 구한다. 수렴조건으로는 연속방정식은 10-5 미만으로 하였고, 에너지방정식은 10-7 미만으로 수렴조건을 정하였다.
2.3 수치해석 결과의 타당성
수치모델의 격자는 사각격자로 하고 벽면에서는 조밀하게 격자를 생성하였으며, 계산영역내의 격자수에 따라 수치해석의 결과가 달라지므로 격자의 의존성을 검토하였다. 그 결과 격자수는 270만개 이상에서는 결과가 수렴하는 것으로 보였다. 그리하여 본 연구에서는 270만개의 격자를 최소 격자수로 하여 수치해석을 수행하였다.
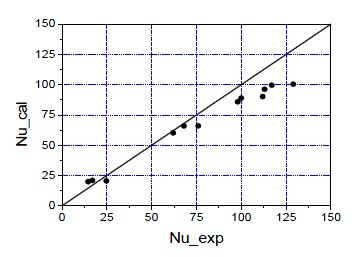
수치해석 결과의 타당성을 확인하기 위해서 Aharwal et al. [5]이 수행한 실험과 동일한 모델에 대해 수치해석을 수행하여 그 결과를 비교하여 Figure 2에 나타내었다. 가로 축에는 Aharwal et al. [5]이 유동방향에 60° 기울어진 연속 립에서 다양한 갭 간격에 따라 Reynolds 수 320017800에 대해 실험하여 얻은 Nusselt 수를 나타내었고, 세로축에는 본 연구에서 검증을 위하여 수치해석으로 얻어진 Nusselt 수를 표시하였다. 대체적으로 실험결과를 잘 예측하지만 Reynolds 수가 높은 영역에서는 다소 낮게 예측하였다. 이는 수치해석을 수행할 때 기하학적 형상은 정확히 일치시켰으나, 경계조건이 실험과 정확히 일치하지 않았고 고 난류영역에서는 난류모델 때문에 수치해석 결과가 실험결과와 다소 차이가 나는 것으로 보인다. 각종 실험오차 등을 감안하면 본 연구의 수치해석 모델은 적절히 예측 가능한 것으로 판단된다
3. 결과 및 고찰
3.1 열전달
삽입한 열전달 향상 장치가 대류 열전달에 미치는 영향을 평가하기 위해서 평균 Nusselt 수를 계산하였다. 평균 Nusselt 수는 다음과 같이 정의하였다.
여기서,
 는 벽면에 공급되는 단위면적당 열전달률이며,
는 벽면에 공급되는 단위면적당 열전달률이며,
 는 벽면 평균온도,
는 벽면 평균온도,
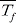 는 입구와 출구 유체의 평균온도를 나타낸다.
는 입구와 출구 유체의 평균온도를 나타낸다.
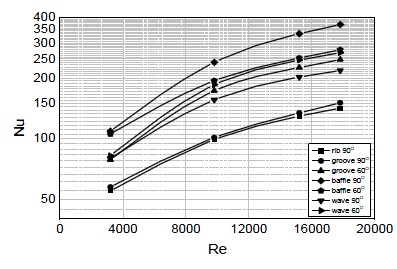
Figure 3은 각각의 형상에 대해 Reynolds 수에 따른 Nusselt 수를 그래프로 나타내었다. 비교적 단순한 모델인 rib 90° 모델이 가장 낮은 열전달 향상 효과를 보였고, baffle 90° 모델에서 가장 높은 열전달 향상 효과를 보였다. 그래프에서 볼 수 있듯이 열전달 향상 효과가 큰 순서는 baffle 90° > baffle 60° > wave 60° > groove 60° > wave 90° > groove 90° > rib 90° 순으로 나타났다. 모든 모델은 Reynolds 수가 증가할수록 열전달 효과가 향상되었으며, 배플을 제외하고는 립이 같은 형상이라도 유동방향에 90°로 배열된 모델보다는 유동방향에 60°로 배열된 모델이 열전달 향상 효과가 높게 나타났다.
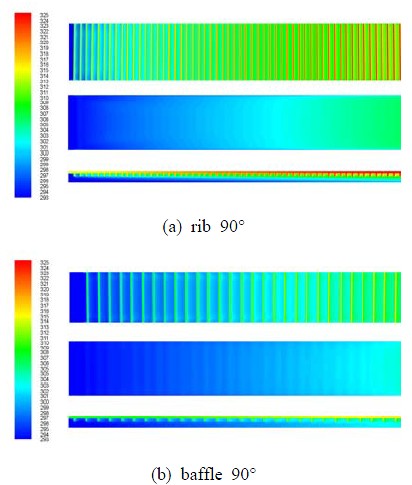
각 모델의 열전달 향상 효과에 대한 원인을 분석하기 위해 채널내 온도분포와 속도분포를 검토하였다. Figure 4는 rib 90° 모델과 baffle 90° 모델에 대하여 덕트의 위에서 바라본 윗면(x-z면, y=25mm) 온도분포와 덕트 중간 지점면(x-z면, y=15mm) 온도분포, 그리고 측면에서 바라본(x-y면, z=0mm) 온도분포를 나타낸 것이다.
그림에서 볼 수 있듯이 열전달 향상 효과가 높은 모델일수록 집열기 윗면의 전체적인 온도가 낮은 것을 알 수 있다. 이는 유입된 유체가 잘 혼합되어 유체가 열을 많이 가져가게 된 것으로 볼 수 있다. 열전달 효과가 가장 좋은 baffle 90° 모델은 윗면과 아랫면에 립이 지그재그 형식으로 배열되어 있어, 가열되는 유체가 윗면의 립과 부딪혀 아래쪽으로 유동방향이 바뀌게 되고 차가운 유체는 아랫면의 립에 부딪혀 위쪽으로 유동방향이 바뀌면서 유동교란이 잘 일어나 유체가 잘 혼합된다. 이로 인해 집열기 흡수평판의 열을 유체가 많이 흡수하게 된다. 반면 열전달 효과가 가장 낮은 rib 90° 모델을 보면 입구에서 유입된 유체가 윗면에서 열전달을 받아 데워지긴 하지만 유동교란이 비교적 작아 잘 섞이지 않고 주유동이 흘러가는 것을 알 수 있고, 흡수평판의 온도가 다른 모델에 비해서 높은 것을 알 수 있다.
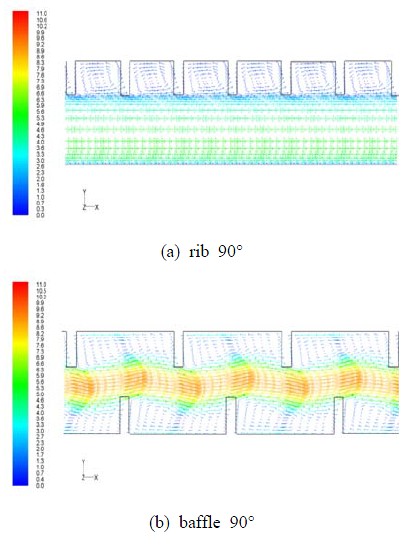
Figure 5는 2가지의 모델에 대하여 덕트의 측면에서 바라본(x-y면, z=0mm) 속도벡터를 나타낸 것이다. 그림을 명확히 나타내기 위해 x=60mm∼120mm 구간만 나타내었다. rib 90° 모델은 전형적인 립과 립 사이에서의 유동을 보여주고 있고, 주 유동은 2차유동에 거의 영향을 받지 않고 흘러가는 것을 볼 수가 있다. 반면, baffle 90° 모델은 윗면의 립 사이와 아랫면의 립 사이에서 2차유동이 발생되며 2차유동이 다시 주 유동공간으로 나오면서 좁아진 주 유동 공간에 모여 덕트 중간에서 속도가 증가하여 빠르게 흘러가는 것을 알 수가 있다.
3.2 압력강하
덕트 내에 열전달 향상 장치를 삽입할 경우 열전달을 증가시킬 수 있지만 배열된 립은 유동을 방해함으로써 압력강하가 커지게 된다. 압력강하가 증가하면 유동에 필요한 동력이 증가하게 되므로 열전달 증가에 따른 이득은 감소하게 된다. 그러므로 열전달 향상 장치를 설계할 때, 압력손실은 중요한 항목이 된다. 압력강하를 구하기 위해 마찰인자를 식 (4)와 같이 정의하였다.
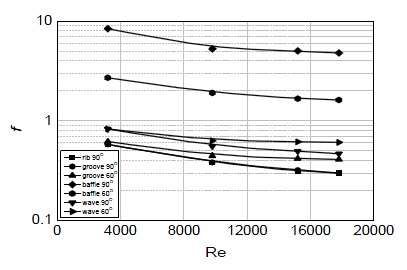
Figure 6은 각각의 형상에 대해 Reynolds 수에 따른 마찰인자를 보여준다. 그림을 보면 baffle 90° 모델에서 마찰인자가 가장 크게 나왔다. 이는 립이 윗면과 아랫면에 지그재그로 붙어 있어 유동교란이 크게 일어나며 다른 모델에 비해 유동의 방해가 커서 압력강하가 크게 나타난다. baffle 60° 모델 역시 압력강하가 크게 나타났으나 baffle 90° 모델 보다 작은 이유는 유동이 보다 자연스럽게 유도되고 있기 때문이다. 그렇기 때문에 같은 형상을 하고는 있지만 각도변화를 이용해서 유동의 흐름을 자연스럽게 함으로써 압력강하를 줄일 수가 있다.
3.3 성능계수
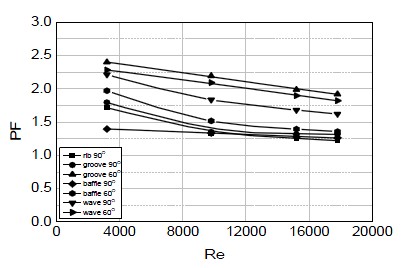
열전달 향상 장치를 삽입하면 열전달은 향상이 되지만 압력손실도 증가하는 것을 보았다. 열전달 성능이 향상하더라도 압력손실이 증가하면 그 만큼 동력이 많이 소요되므로, 식 (5)와같이 정의되는 일정한 송풍력에서 압력손실에 대한 열전달 비인 성능계수(Performance factor; PF)[12]를 계산하여 이 값이 높아졌는가를 확인하여야 한다.
여기서, Nus와 fs는 열전달 향상 장치가 삽입되지 않은 매끈한 덕트에서의 Nusselt 수와 마찰인자이다.
Figure 7은 성능계수를 Reynolds 수에 따라 나타낸 것이다. 성능계수는 Reynolds 수가 증가할수록 감소하였다. 이는 Reynolds 수가 증가할수록 열적성능의 증가에 비해서 압력강하의 증가 비율이 커지기 때문에 성능계수가 감소한다. 그리고 가장 좋은 성능계수를 나타낸 것은 groove 60° 모델이고, 다음으로 wave 60° 모델이 좋았다. 성능계수가 높은 영역에 포함된 두 모델들은 열적성능이 가장 좋거나 압력강하가 가장 낮은 것은 아니었다. 이는 열적성능이 가장 좋거나, 압력손실이 가장 낮다고 하여 좋은 열전달 향상 장치가 될 수 없다는 것을 말한다. baffle 90° 모델을 보면 열전달 측면에서 가장 높았지만 압력강하 역시 가장 높아 성능계수에서는 낮은 영역에 포함이 되었다. 그러므로 반드시 성능계수를 파악하여 설계할 필요가 있다.
4. 결 론
본 연구에서는 평판형 태양열 집열기에 여러 가지 형상 및 배열의 열전달 향상 장치를 삽입하여 Reynolds 수에 따라서 열전달 및 압력강하에 대한 특성을 수치해석을 통하여 연구하여 다음과 같은 결론을 얻었다.
(1) 윗면과 아랫면에 립이 지그재그 형식으로 배열된 baffle 90° 모델이 열전달 향상 효과가 가장 좋았으며, 단순한 형상인 rib 90° 모델이 가장 낮았다.
(2) 단순한 형상인 rib 90° 모델은 유동의 교란이 작아 압력강하가 가장 낮으며, 유동 교란이 크게 일어난 baffle 90° 모델에서 압력강하가 가장 높게 나타났다.
(3) 같은 형상의 립을 삽입하더라도 유동방향에 90°로 배열된 립보다는 유동방향에 60°로 기울어져 배열되어 있는 모델이 열전달이 잘 되었고, 압력강하는 낮게 나왔다.
(4) groove 60° 모델에서 가장 높은 성능계수가 나타났다. 반면, 열전달 효과가 가장 높게 나온 baffle 90° 모델은 압력강하가 다른 형상들에 비해 훨씬 높게 나왔기 때문에 성능계수가 비교적 낮았다.
(5) 열전달 향상 장치를 설계를 할 때 열전달이 가장 높거나 압력강하가 가장 낮은 모델을 선택하는 것이 아니라 성능계수를 파악하여 이득과 손실을 고려하여 가장 효율적인 형상을 선택해야 한다.
Acknowledgments
이 논문은 2012학년도 동의대학교 교내연구비에 의해 연구되었음.(과제번호: 2012AA156)
References
- R. Manglik, A. Benjan, and A. D. Kraus, Heat Transfer Handbook, John Wiley & Sons Inc, (2003).
-
V. S. Hans, R. P. Saini, and J. S. Saini, "Performance of artificially roughened solar air heaters - a review", Renewable and Sustainable Energy Reviews, 13, p1854-1869, (2009).
[https://doi.org/10.1016/j.rser.2009.01.030]

-
J. H. Kim, J. N. Heo, S. H. Ahn, D. H. Lee, Y. S. Son, and J. Y. Shin, "Numerical analysis on heat transfer and pressure drop characteristics in a horizontal channel with various ribs", Journal of the Korean Society of Marine Engineering, 37(1), p40-46, (2013), (in Korean).
[https://doi.org/10.5916/jkosme.2013.37.1.40]

-
B. Bhushan, and R. Singh, "Nusselt number and friction factor correlations for solar air heater duct having artificially roughened absorber plate", Solar Energy, 85, p1109-1118, (2011).
[https://doi.org/10.1016/j.solener.2011.03.007]

-
K. R. Aharwal, B. K. Gandhi, and J. S. Saini, "Experimental investigation on heat-transfer enhancement due to a gap in an inclined continuous rib arrangement in a rectangular duct of solar air heater", Renewable Energy, 33, p585-596, (2008).
[https://doi.org/10.1016/j.renene.2007.03.023]

-
S. V. Karmare, and A. N. Tikekar, "Heat transfer and friction factor correlation for artificially roughened duct with metal grit ribs", International Journal of Heat and Mass Transfer, 50, p4342-4351, (2007).
[https://doi.org/10.1016/j.ijheatmasstransfer.2007.01.065]

-
V. S. Hans, R. P. Saini, and J. S. Saini, "Heat transfer and friction factor correlations for a solar air heater duct roughened artificially with multiple v-ribs", Solar Energy, 84, p898-911, (2010).
[https://doi.org/10.1016/j.solener.2010.02.004]

-
E. K. Akpinar, and F. Kocyigit, "Experimental investigation of thermal performance of solar air heater having different obstacles on absorber plates", International Communications in Heat and Mass Transfer, 37, p416-421, (2010).
[https://doi.org/10.1016/j.icheatmasstransfer.2009.11.007]

-
A. Kumar, J. L. Bhagoria, and R. M. Sarviy, "Heat transfer and friction correlations for artificially roughened solar air heater duct with discrete w-shaped ribs", Energy Conversion and Management, 50, p2106-2117, (2009).
[https://doi.org/10.1016/j.enconman.2009.01.025]

-
S. Singh, S. Chander, and J. S. Saini, "Heat transfer and friction factor correlations of solar air heater ducts artificially roughened with discrete v-down ribs", Energy, 36, p5053-5064, (2011).
[https://doi.org/10.1016/j.energy.2011.05.052]

- FLUENT, "FLUENT 6.3 manual", (2009).
-
R. L. Webb, and D. L. Gee, "Forced convection heat transfer in helically rib-roughened tubes", International Journal of Heat and Mass Transfer, 23, p1127-1136, (1980).
[https://doi.org/10.1016/0017-9310(80)90177-5]